基于动态分区的网格水文模型分布式计算
王继民,刘赛佳,李嘉玮
(河海大学 计算机与信息学院,江苏 南京 211100)
0 引 言
网格水文模型属于分布式水文模型[1]的一种,它将流域划分为多个网格单元,每个网格具有独立的参数,能够更加精细化考虑流域各种地理要素的空间异质性,是解决众多水文实际问题的有效工具。姚成等[2]提出网格新安江模型并将其应用于密赛流域,实验验证网格新安江模型相比于传统的新安江模型能取得较高的模拟精度。
目前提高水文模型计算效率的方法多采用并行化计算框架[3]。Yue等[4]提出一种将分布式水文模型的计算流域划分为大量子流域的并行计算方案,提高了模型计算效率。Chu等[5]提出了基于静态任务分解的坡面-河道并行计算策略,提高了河流演算的并行效率。但并行计算方式当模拟单元单一化时性能提升效率有限[6],数据分区可以根据节点的计算能力为其分配不同的计算任务,从而提高并行计算的效率[7]。陈迪等[8]对Spark数据分区机制进行优化,基于微任务的思想,减轻了数据倾斜对整体系统性能的影响。朱迅等[9]提出了一种基于异构Spark集群的分区动态负载的调度算法,加快了Spark在异构集群及集群复杂负载情况时的运行速度。
虽然已有的并行化计算研究取得了一定的成果,但没有细致考虑每个网格、模型每个步骤之间的并行关系。基于此,本文首先根据网格汇流流向特点,提出了动态数据分区方法,并在此基础上提出了基于Spark的网格化水文模型分布式计算模型,并通过实验验证了所提模型的计算效果。
1 基于网格汇流的动态数据分区方法
在网格水文模型分布式计算过程中,通常网格计算次序对应的网格数量不同且差异较大,直接使用Spark的数据分区器会因计算次序选取不当出现数据分区不平衡形成的数据倾斜现象[10]。这里的数据倾斜是指每个分区内网格数量差异很大,这使得各分区任务执行时间差异较大,网格数量较少的任务执行完毕后对应的worker节点将处于空闲状态,这导致了集群资源的极大浪费。
本节根据网格汇流流向的参数特点,将多个网格单元动态合并为若干个大小近似且可同时计算的网格集合,有效地解决了数据倾斜问题,并为分布式模型的计算提供了有力的支撑。
1.1 网格数据分区总体流程
网格数据分区主要包括网格数据分区单次计算过程以及网格单元更新操作。单次的数据分区计算过程包括计算集群的可用资源、根据网格流向计算上游网格坐标、根据网格计算次序计算每个次序对应的网格个数,根据上述3个步骤计算结果对流域网格进行动态分区;网格单元更新操作是对上一轮数据分区的上游网格参数进行更新,剔除已完成计算的网格,重新进行动态数据分区操作。根据单次数据分区计算结果对网格单元信息进行更新并再次进行数据分区的过程称为网格数据分区循环计算流程。
1.2 网格数据分区单次计算流程
网格数据分区单次计算方法可以将满足分区要求的计算次序对应的网格及其所有的上游网格根据分区数进行均等划分,减轻在集群计算的过程中出现数据倾斜现象,并且在之后的计算过程中对参与分区的所有网格同时计算,不再需要大量的数据聚合操作,减少了数据交互的次数。网格数据分区单次计算流程如图1所示。

图1 网格数据分区单次计算流程
网格数据分区单次计算的具体过程如下所示:
(1)计算集群的最大并行数Max。记集群中共有N个同构的计算机作为Worker节点,第CeilNum个节点中有Ei个Executor执行器,每个执行器有Ci个Core。集群的最大并行数由式(1)决定
(1)
(2)计算每个网格单元对应的所有上游网格坐标和数量。根据网格汇流流向参数计算出每个网格对应的所有上游网格坐标并以 “x1,y1,x2,y2…” 的格式存储在字符串数组UpCeil中。遍历UpCeil数组,其长度记为Len, 则该上游网格的个数为Len/2, 并用数组UpCeilLen存储,即UpCeilLen[x][y]=k表示坐标为 (x,y) 的网格单元的上游网格为k个。
(3)计算每个网格计算次序对应的网格坐标及数量。令无上游网格的网格单元计算次序为1,其余网格的计算次序由上游网格的最大计算次序加1。每个计算次序对应的网格坐标以 “x1,y1,x2,y2…” 的格式存储在字符串数组Order-Ceil中。计算每个网格计算次序对应的网格数量,用整型数组OrderCeilNum存储。即OrderCeilNum[p]=q表示计算次序p对应网格个数为q个。
(4)初始化分区数。划分的分区数用CeilNum表示,在模型计算初始化时令分区数为Max。
(5)从大到小选择网格个数大于等于CeilNum的计算次序。如果该次序不存在,执行CeilNum递减操作,最大程度的利用集群资源。假设满足条件的最大计算次序为P,对应的网格单元个数有K个,其中K≥CeilNum。 这K个网格单元对应的上游网格数量用集合T表示,如式(2)所示
T={c1,c2,c3,…,ck}
(2)
其中,ci表示第i个网格单元对应的上游网格数量。
(6)计算分区理想情况下的网格个数GNumequals并定义数据倾斜可接受范围Q。数据倾斜即为分区之间数据量大小不同,Q越大表示分区之间数据大小差值的接受度越高。为了防止因Q过小出现无满足条件的计算次序的问题,Q随着循环计算次数的增加而增大,即每循环一次Q为原来的二倍。理想情况下各个分区网格个数GNumequals的计算方法如式(3)所示
(3)
(7)对于满足条件的K个网格单元,将每个网格坐标及其对应上游网格坐标作为一个整体进行数据划分,根据数组UpCeilLen中K个网格的上游网格长度将这K份网格尽可能均等划分为CeilNum份,得到的分区网格数量可以用集合Nums表示,如式(4)所示
Nums{num1,num2,num3,…,numCeilNum}
(4)
其中,Numi表示第i个分区划分得到的网格单元数量。
(8)若最终的分区个数小于等于集群最大并行数Max, 不再进行分区条件判断,直接结束数据分区过程。否则需要对集合Nums中的网格个数进行判断,若对于集合Nums中任意的numi, 都满足式(5),则此次分区操作结束。否则意味着出现了不可接受的数据倾斜现象,需要重新进行网格数据分区操作,直到满足条件为止。为了快速寻找到下一个满足条件的计算次序,本方法将CeilNum的增量设置为Max, 即下次的分区操作的分区个数CeilNum=CeilNum+Max
GNumequals*(1-Q)≤numi≤GNumequals*(1+Q)
(5)
1.3 网格数据分区循环计算流程
1.2节详细的介绍了网格数据分区方法的单次计算流程,该方法在保证水文模拟过程正确的情况下,尽可能将网格动态划分为多个大小相近、可以同时计算的网格集合。但是一次的网格分区操作并不能完成整个流域的水文模拟过程,因此,本小节设计了网格数据分区循环计算方法。该方法对上次分区结果对存储网格信息变量进行更新并重新进行数据分区操作。网格数据分区循环计算具体的过程如下:
(1)初始化网格单元标志位参数flag[][]。 若flag[i][j]=0则表示坐标为 (i,j) 的网格未进行分区计算,若flag[i][j]=1则表示坐标为 (i,j) 的网格已经完成分区计算。
(2)调用网格数据分区单次计算方法。由于上游网格信息更新取决于上次的数据分区涉及的网格,所以需要先进行一次数据分区操作。
(3)获取网格数据分区操作中选择的计算次序K。若K等于当前流域网格的最大计算次序,则说明所有网格计算完毕,结束数据分区循环操作。否则进入步骤(4)。
(4)获取已分区网格坐标。对于步骤(2)计算过程中已进行分区的网格坐标使用字符串数组进行存储,网格坐标形式依然为 “x,y”。 令flag[x][y]=1, 表示这些网格不再进行分区计算。
(5)遍历计算次序大于K的网格对应的上游网格坐标,从中剔除flag为1的网格单元。根据更新之后的上游网格坐标数组UpCeil, 计算上游网格个数并对上游网格数量数组UpCeilLen进行更新。更新完之后再次调用网格数据划分单次计算方法,直至步骤(3)中的计算次序等于流域网格的最大计算次序。
2 基于Spark的网格水文模型分布式计算模型
模型的总体结构如图2所示,共包括四大部分:模型参数描述规范、模型构建及依赖描述规范、构件任务调度及计算、计算结果整合。模型参数描述采用了NetCDF(network common data form)规范对网格水文模型参数进行统一的描述[11,12];模型构件及依赖关系描述采用XML(extensible markup language)规范进行描述;构件任务调度及计算指的是通过解析NetCDF的网格水文模型参数文件以及模型构件及依赖关系描述文件,获取参数与构件信息,在分布式计算过程中采用不同的数据分区方法进行网格分区,调用构件计算文件进行计算;计算结果的整合以NetCDF的形式进行保存。
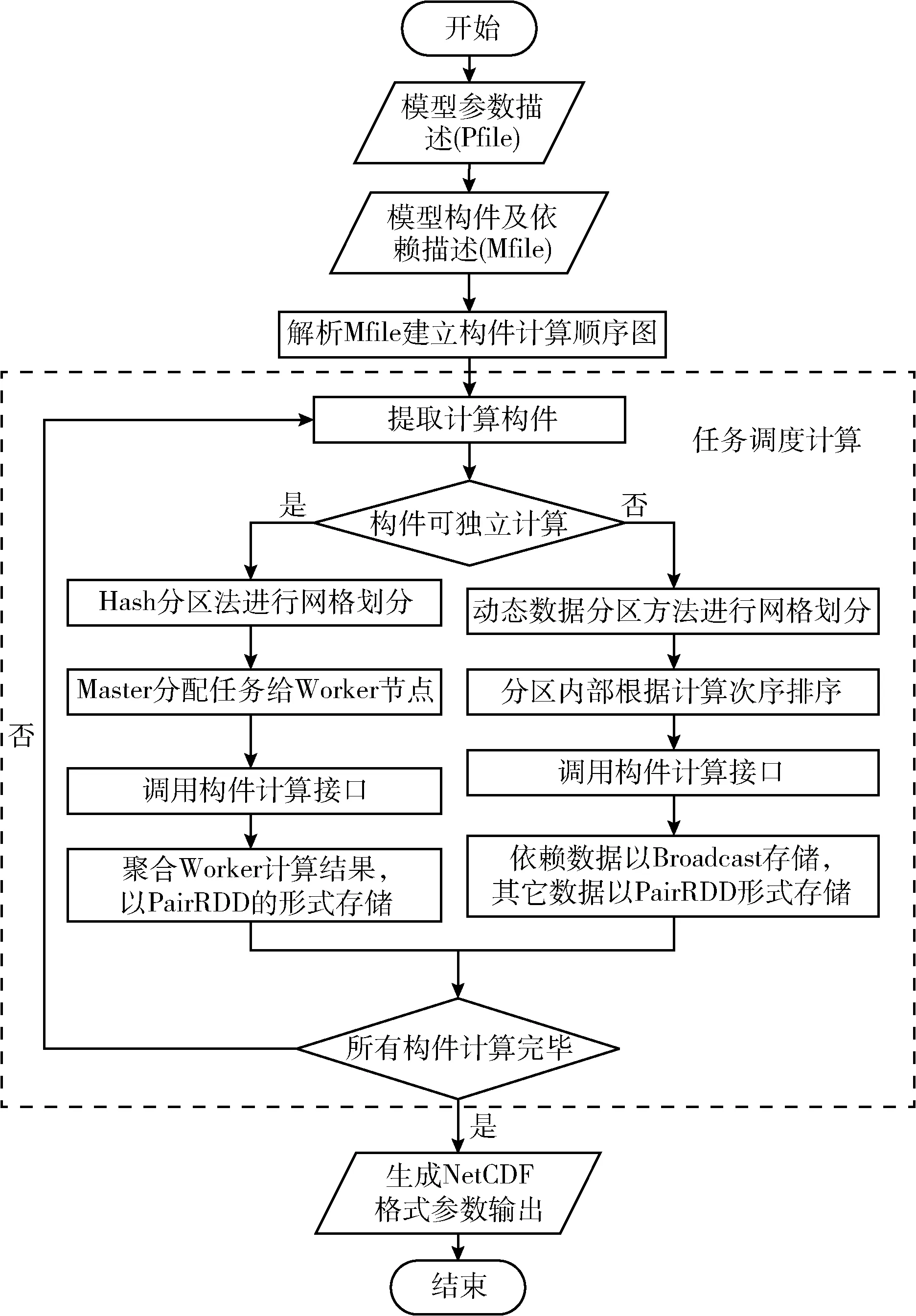
图2 模型总体结构
2.1 基于NetCDF的网格水文模型参数描述
网格水文模型参数包括三大类型:模型参数、流域基本信息参数和流域实时信息参数。
(1)模型参数
模型参数在程序设计中对应的是数值型变量。对标量参数的描述从变量标准名称(standard_name)、单位(units)和取值范围(valid_range)这3个方面进行描述。其中standard_name在参数描述中为必要属性,valid属性和units属性为非必要属性。
(2)流域基本信息参数
流域基本信息参数的存储形式为二维数组。在上述信息描述的基础上,从标准名称(standard_name)、取值范围(valid_range)、无效值(_FillValue)和单位(units)这4个方面对流域基本信息参数进行描述。
(3)流域实时信息参数
流域实时信息参数比流域基本信息参数多一维时间维度为三维数组。因此在流域基本信息描述的基础上增加对时间序列的描述即为流域实时信息参数的描述方法。流域实时信息参数的时间序列分为两种类型,一类由连续的时间序列构成,这类数据的时间维度变量值可以为空,参数值的时间点个数根据模型参数中的开始时间、结束时间和时间间隔计算得出;第二类为包含间隔点的时间序列,当时间出现断点的时候,需要用数组的形式对有记录的时间点进行存储。
2.2 基于XML的网格水文模型构件及关系描述
网格水文模型一般是由多个构件组成,根据各构件的计算特点,将网格水文模型构件分为独立计算构件、数据依赖构件和参数聚合构件。
独立计算构件是在单个网格单元中的计算过程并不涉及其它网格单元的参数信息的一类构件,数据依赖构件指的是在计算过程中需要依赖网格的上游网格的参数信息的一类构件,参数聚合构件用于各个构件计算结果的聚合以及结果保存操作,负责将各个模块的计算结果以NetCDF的形式保存到指定路径中,不属于按照水文模拟过程划分的构件。
网格水文模型的构件(components)描述属性一般包括构件名称(componentName)、构件编号(conponentId)、构件存储路径(componentPath)、构件函数入口(componentFuction)、参数路径(paramPath)、前置构件标识(precoms)、结果输出路径(resultOutPath)、依赖参数标识(relParamId)、构件计算类型(componentType)和构件保存类型(saveType)这10个方面的基本信息,其中依赖参数标识为数据依赖构件特有的子元素,用来存储依赖参数的标识,便于依赖数据交互操作。构件描述的结构如图3所示,其中componentType属性取值有0、1和2这3种,0代表该构件为独立计算构件,1代表该构件为数据依赖构件,2代表该构件为参数聚合构件;saveType属性取值为0和1两种,0代表exe存储方式,1代表Jar包存储方式。
2.3 构件调度及计算
2.3.1 独立计算构件分布式计算过程
独立计算构件的分布式计算相对简单,不需要考虑网格单元之间的数据依赖问题。关于独立计算构件分布式计算流程具体步骤如下:
(1)获取构件计算所需参数。首先解析NetCDF文档得到构件计算所需参数。将解析到的流域基本和实时参数以网格为单位使用字符串数组的形式进行存储。
(2)参数格式转换。获取网格参数信息之后,将其转化为Spark的RDD的形式。解析网格参数字符串信息,获取网格单元的计算次序作为Key,将整个参数字符串作为Value,将RDD转换为PairRDD形式[13-15]。
(3)根据网格计算次序进行排序操作。该步骤主要是根据Key值对PairRDD进行排序,便于数据依赖构件的计算。
(4)网格参数分区操作。独立计算构件使用Spark中自带的HashPartitioner分区器进行分区,因为该构件计算与网格单元的计算次序无关,所以不需要根据网格流向进行数据划分。
(5)构件计算。该步骤主要是执行构件算法的代码,将解析之后的网格参数传递到构件函数中。
(6)结果处理。完成步骤(5)之后就可以得到构件的计算结果,计算结果一般为与时间相关的一组参数。构件的计算结果以NetCDF的形式进行存储。
2.3.2 数据依赖构件分布式计算过程
数据依赖构件的计算过程并不完全是网格独立的,在计算过程中涉及到上游网格单元的计算结果,需要使用基于网格流向的Spark动态数据分区算法,可以减少各分区网格数量的差异,同一计算次序对应的网格及其上游网格也可以同时计算,从而提高模型的计算效率。数据依赖构件分布式计算流程如图4所示。
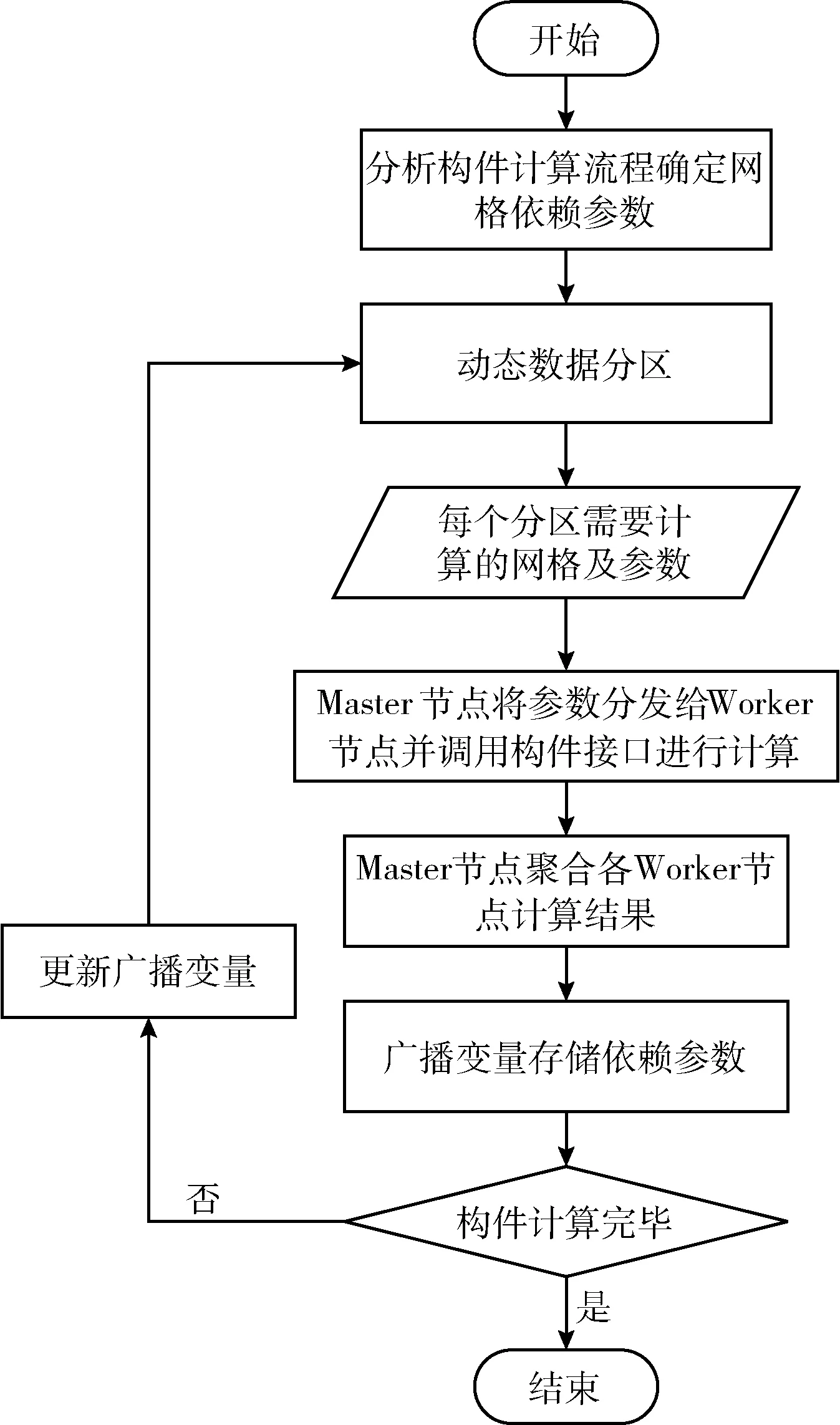
图4 数据依赖构件分布式计算流程
数据依赖构件计算的具体过程如下:
(1)参数预处理。通过分析构件计算流程,确定网格依赖参数。将读取的参数转化为Spark计算需要的PariRDD格式,其中Key为网格坐标,Value为参数值。
(2)动态数据分区方法进行分区操作。通过动态数据分区方法,确定每个Worker节点需要计算的网格,将对应的网格参数传输到相应的节点上,Worker节点调用构件计算接口,进行构件计算,执行完成之后将该网格的flag[x][y] 置为1。
(3)计算结果聚合。Master节点聚合各个Worker节点的计算结果,并将网格依赖的参数存储到广播变量中。
(4)更新广播变量。步骤(3)所计算的网格单元的部分计算结果需要作为下一批网格的输入参数,对计算结果进行解析,获取共享变量对应的计算结果并进行更新,将更新的结果重新分发出去。
(5)判断网格是否计算完毕,若没有计算完毕,则进行步骤(2)再次进行分布式计算操作,直至所有网格计算完成。
3 分布式计算模型验证
本节以网格新安江模型为实验模型,以屯溪流域为实验流域,实验分为两部分,第一部分验证动态数据分区的有效性。第二部分验证本文模型在Spark本地模式和Standalone模式下计算效率的提高。
第一部分实验采用Java编写的网格新安江水文模型对屯溪流域水文模拟的汇流过程数据分区进行对比,实验数据为屯溪流域网格划分数据、网格流向参数和网格单元计算次序参数。
实验分别使用本文提出的基于网格汇流的Spark动态数据分区方法与基于集群最大并行数的Spark静态数据分区方法对屯溪流域进行网格单元划分,并对使用这两种方法划分得到的分区网格数量差异进行对比,设置分区数分别为4和6,Q为0.1。
4分区当且仅当计算次序为21时候满足动态分区的阈值要求且并行数为4,将本次实验的结果与Spark静态分区方法进行对比,4分区结果对比如图5所示。
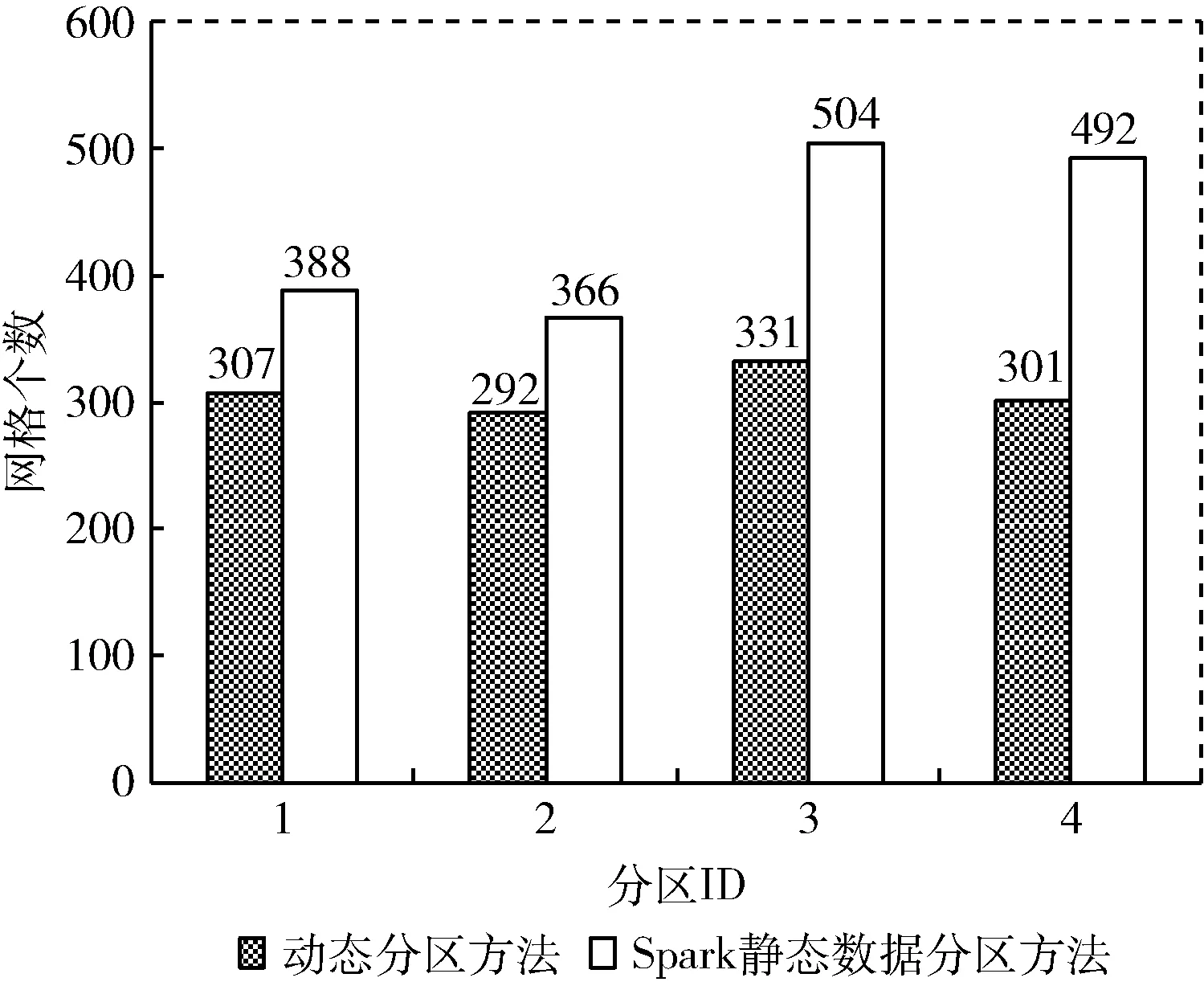
图5 4分区结果对比
如图5所示,网格计算次序21对应的动态数据分区方法得到的分区结果的最大值331与最小值292的差值在平均值的10%以内,但是Spark静态数据分区方法对应的分区网格个数的最大值504与最小值366的差值超过了平均值的20%。
6分区时需要8次分区即可完成屯溪流域网格的划分操作。将前两次分区数为6的分区结果合并与Spark静态分区方法得到的分区结果进行对比,6分区结果对比如图6所示。
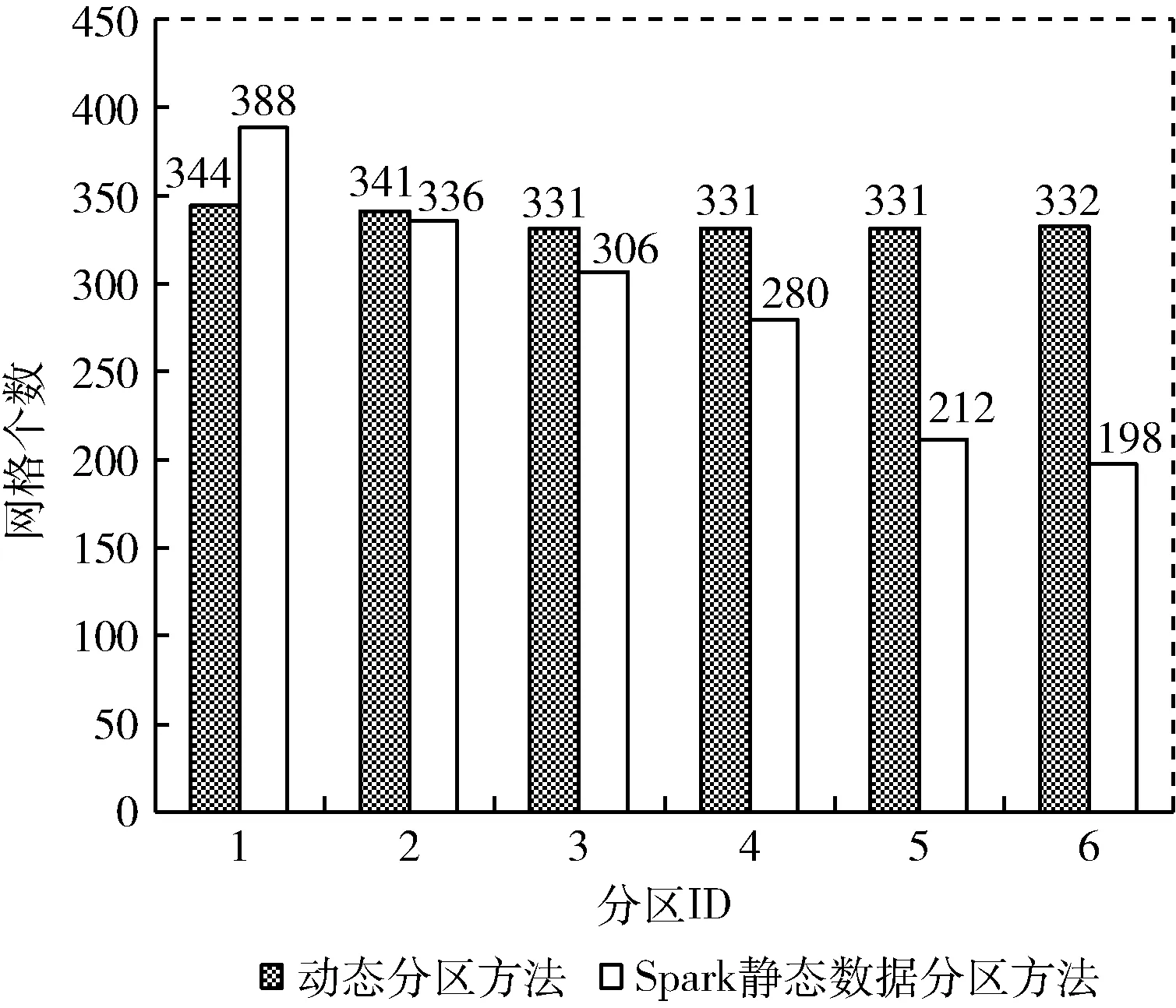
图6 6分区结果对比
图6中的动态分区方法的结果各个分区的最大值与最小值的差值均小于平均值的10%;使用Spark静态分区方法得到的分区结果的最大分区网格个数为388,最小分区网格个数为198,两者之间的差值远高于平均值的10%。
由第一部分实验可以得到本文提出的动态数据分区方法能保持较好的分区数据平衡性,且适应于不同的分区数情况。通过与Spark静态分区结果进行对比,验证了本文方法在解决网格水文模型数据分区中的数据倾斜问题的有效性。
第二部分实验分为两组,第一组使用一台PC机,内存大小为24 G,CPU型号为i5-7900HQ。第二组集群由3台1核CPU、4 G内存虚拟机构成,两组实验的分布式计算模型的分区数均为4。
(1)Spark本地模式本文方法与网格新安江模型串行计算方法对比。
对于第一组实验中3天~27天的预热期(从实测开始时间到预报开始时间的时间间隔),分别使用上述两种模型对网格新安江模型进行计算,网格新安江模型计算时间结果对比如图7所示。每一次计算的具体时间见表1。

图7 网格新安江模型计算时间结果对比
由图7和表1可知,随着水文计算时间的延长,本文提出的网格水文模型分布式计算模型的优势逐步显示出来。在预热期小于24天的时候,与已有的网格新安江模型串行计算方法相比,分布式计算模型的加速比逐步增加。水文模拟时间为15天时,分布式计算模型的运行效率是串行计算模型计算效率的2.46倍,水文模拟时间达到24天时,计算效率提升至2.68倍。水文模拟时间为27天时,已有网格新安江模型串行计算方法出现了内存溢出的情况,无法再进行模型计算,而分布式依然保持着较好的运行速率。
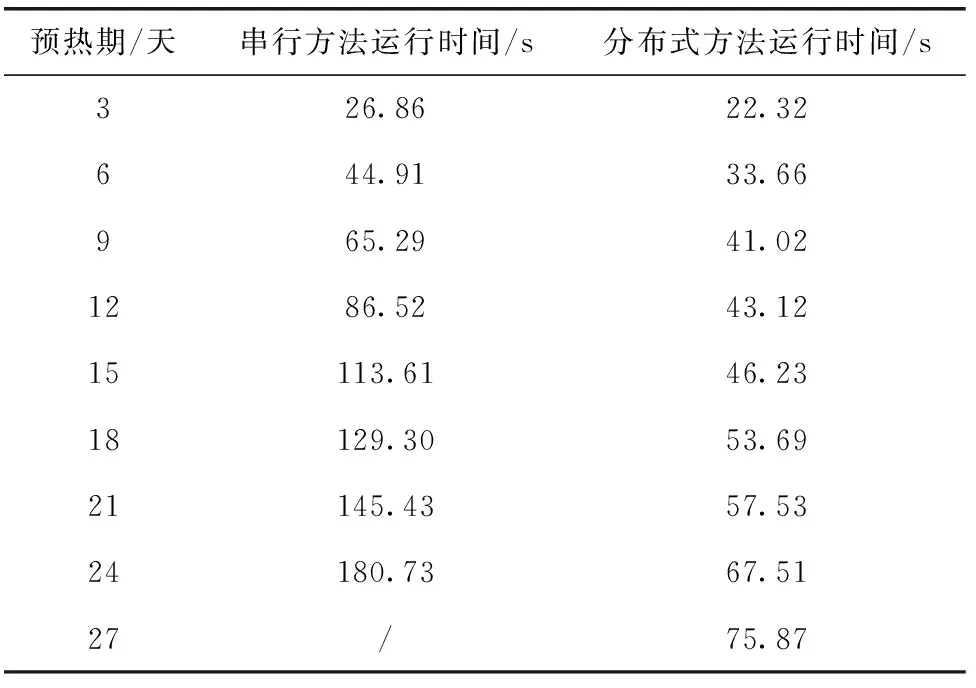
表1 串行计算与分布式计算方法结果
图8为网格新安江模型长历时水文模拟分布式计算方法运行结果图,分别对1个月、2个月、3个月时长水文模拟进行计算。为了延长模型可计算的水文模拟时间,本模型根据计算的水文模拟时长度,每增长一个月的预热期,就增加分区数,即一个月水文模拟计算的分区数为4,两个月水文模拟计算分区数为8,3个月水文模拟计算的分区数为12,防止单个任务过大引起的内存溢出问题。

图8 网格新安江模型长历时水文模拟分布式计算运行时间结果
(2)Spark的Standalone模式下本文模型与基于网格计算次序并行化的计算思想实现的分布式计算模型对比。
由于实验环境的限制,无法在Standalone模式下进行长时间的水文模拟计算。分别在Standalone集群模式下对3天水文模拟时长至27天水文模拟时长中的8组时长进行实验。图9为两种方法在Standalone集群模式下的运行时间结果,每次计算的具体时间见表2。
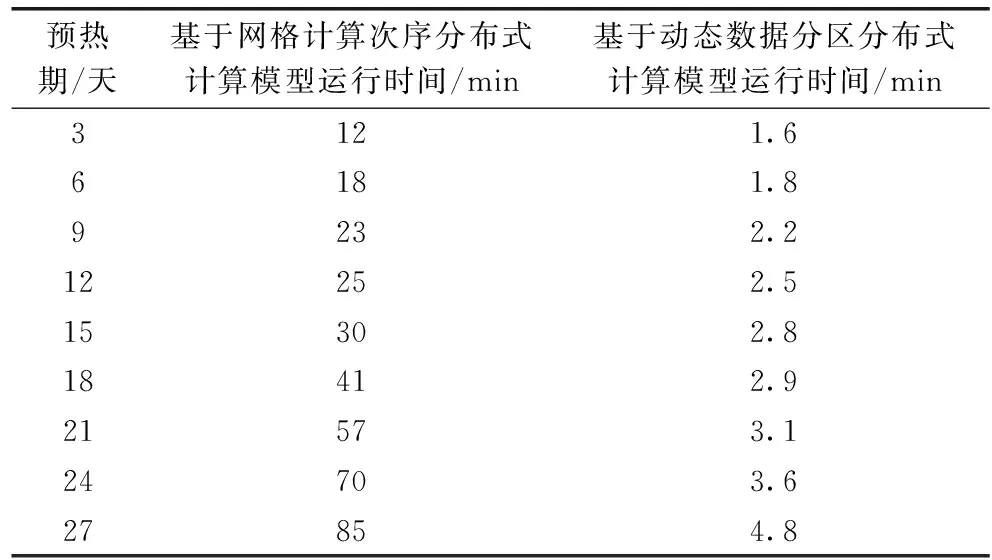
表2 Standalone模式下模型计算时间结果

图9 Standalone模式下模型计算时间结果
屯溪流域网格新安江模型的网格单元计算次序最大为100,在基于网格计算次序分布式计算模型中,对于相同计算次序的网格单元计算完成之后进行数据聚合操作,再进行
下一步的计算。因此,该模型在汇流构件至少有100次数据聚合操作。而本文的分布式计算模型根据网格流向将流域网格划分为多个网格集合,在整个分布式计算过程中只需要4次的数据聚合操作,解决了因为频繁的数据交互操作造成计算时间过长的现象。从表2可以看出,使用动态数据分区方法构建的分布式计算模型,在Standalone集群模式下计算效率有大幅度的提升。
从上述两组实验可知,无论是在一台计算机中使用Spark的本地模式还是由多台计算机构成的Standalone模式,本文提出的网格水文模型分布式计算模型均能够明显提高模型计算效率,且能够有效延长水文模拟总体时长。在第二组实验中,将网格新安江模型的数据交互次数从100降至4次,再次验证了本文提出的基于网格流向的Spark动态数据分区方法在减少数据聚合操作方面的有效性。
4 结束语
为了提高网格水文模型的计算效率,本文致力于研究基于多台性能有限的计算机集群环境下的网格水文模型高效计算方法,根据网格流向参数特点,提出了基于网格流向参数特点的动态数据分区方法,有效解决了网格水文模型分布式计算过程中出现的数据倾斜问题,并在此基础上提出了基于Spark的网格水文模型分布式计算模型,并通过实验验证了该模型带来的计算效果的提升。

