基于事务分离的差分隐私频繁项集挖掘方法
丁苏凡,曾尚琦,田冬艳
(1.中国矿业大学 信息与控制工程学院,江苏 徐州 221000; 2.国电南瑞科技股份有限公司 国网电力科学研究院,江苏 南京 211000)
0 引 言
关联规则研究是数据挖掘中关键课题,用于发现不同物品、信息之间的关联。频繁项集挖掘是发掘关联规则中的重要部分,通过大量研究发现,将采集的数据集进行频繁项集挖掘、关联规则分析以后直接将结果发布会导致个人隐私暴露[1,2],若被不法分子加以利用会造成不良后果。就此问题,在利用大量私人数据进行数据挖掘用于生产的过程中,加强隐私保护并提高数据可用性是当前需要进一步解决的问题。现有的隐私保护方法大多基于k匿名[3]及其拓展模型[4-6]。由于这两种模型都只能抵挡特定的攻击方法,所以当面临的攻击者拥有强大的知识背景的情况下,这种隐私保护模型就难以对用户的隐私信息提供有效的保护。差分隐私模型(differential privacy)的提出解决了上述的问题,此方法是向需公开的数据集或是被请求的数据集中加入扰动信息,从而避免隐私泄露[7]。近年来,有关差分隐私保护下的频繁项集挖掘算法研究成果很多。BHASKAR.R是此算法的奠基人,提出了基于指数机制(exponential mechanism)和拉普拉斯机制(Laplace mechanism)的TF算法[8]。TF算法取前k个支持度高的作为频繁项集,该方法避免了在加噪过程中导致的频繁项集变不频繁的传输误差。并且满足差分隐私保护的要求,缺点是当k较大时,此算法无法保证输出数据的准确性。为了解决此问题,PrivBasis算法产生了。DP-topk算法先采用FP-Growth算法进行项集的挖掘,然后采用指数机制将事务进行数据截断处理[9],再采用拉普拉斯机制进行支持度加噪使其输出的数据满足差分隐私。这种将对支持度的处理后置的方法,降低了算法中加入的噪声。
1 理论基础与问题描述
1.1 差分隐私
差分隐私技术能达到保护数据中的个人隐私的目的是通过向采集的数据集中加入噪声的方法,使得输出的数据失真,并且产生的结果不再为一固定值,而是具有随机性;结果的随机性可以保证即使攻击者拥有相关的一系列相关的知识背景,也无法获取原始数据集。从而保护了用户隐私[10]。
定义1 邻近数据集:设一个数据集为一个集合N={n1,n2,…nm}, 另一个数据集为N′={n′1,n′2,…n′m}, 若这两个集合中只有一个ni≠n′i, 其余都相等。则称这一对数据集为邻近数据集。
定义2ε-差分隐私[11]:将算法K作用在两个相邻数据集N与N′上,输出S为K值域的子集。若算法K满足不等式(1),则算法K满足ε-差分隐私,ε表示隐私保护的标准
Pr[K(N)∈S]≤eε×Pr[K(N′)∈S]
(1)
定义3 全局敏感度[12]:对于任何查询函数q,我们将Δq定义为当应用于查询函数的两个相邻数据集的输入时,输出结果的最大的差异
(2)
定理1 差分隐私保护的串行性质:设N是一个数据集,若n个查询算法K={K1,K2,…,Kn} 同时作用于这个数据集上,并且每个查询算法对数据集N进行隐私保护处理以后,都能保证算法输出结果满足ε-差分隐私保护,则称这一系列算法所构成的组合满足ε-差分隐私保护。
1.2 保护模型
目前差分隐私保护模型主要有两种,分别是拉普拉斯机制和指数机制。这两种机制分别适用于不同的数据类型,前者适合在连续型数据中加噪,后者适用于离散型数据中加噪,两者都是通过对所要发布的或是被请求的原始数据集添加扰动机制来进行数据隐私保护,并从数学意义角度严格定义了一种隐私理论的框架。
定理2 拉普拉斯机制(Laplace mechanism)[13]:其基本思想是对数据集N用查询函数q进行查询,再向查询结果中加入满足拉普拉斯噪声分布的x,其概率密度函数为
(3)
对于函数q:N→Rn来说,如果差分隐私算法M的输出结果满足式(4),则M满足ε-差分隐私算法。可以看出,全局敏感度与噪声大小成正比

(4)
定理3 指数机制(exponential mechanism)[14]:指数机制由一个可能输出的有限集O(称为范围)和一个实值函数q:Dn×R×R参数化,它根据输入算法M,为每个可能的输出r分配一个分数q(M,r)。 给定O、q、T和ε,产生尽可能高分数的输出结果。若算法M满足式(5),则隐私保护算法M提供ε-差分隐私保护
(5)
由式(5)可知,评价函数是关键,评价分数越高的时候输出项r被选择输出的概率也就越大。
1.3 问题描述
频繁项集挖掘[15]过程中进行隐私保护,多采用对支持度进行拉普拉斯加噪方式提供ε-差分隐私保护。拉普拉斯加噪机制主要是将函数的全局敏感度和差分隐私预算的比值作为主要调节的参数,用来控制加噪的大小。由定义2可知,当输入两个相邻数据集后,输出的概率比值无限接近于1时,此结果表明隐私预算ε很小的前提下,对于相邻数据集结果进行查询,得出同一结果的概率非常相近,即隐私保护水平越高。当ε趋于0时,加入的噪声非常大,会导致数据可用性很低。并且根据全局敏感度的定义可以知道,全局敏感度越大对应添加的噪声越大,以至于数据的可用性越低。为了增加数据可用性,可以通过降低全局敏感度的方式解决问题。又因为相邻数据集可以等效为对同一数据集增加一条事务或减少一条事务,由此可知,当数据集增加一条很长的事务,这条事务中每个项的支持度也会对应增加1,这会导致敏感度大幅增长。根据敏感度增加的问题,本文采取限制事务长度的办法,进而降低敏感度、提高数据集的可用性。
2 基于事务分离的差分隐私频繁项集挖掘
现有限制事务最大长度的方法是在挖掘频繁项的过程中,先将较长的事务中的非频繁项剔除,但当一个事务包含过多的频繁项集的情况下,即使去除了非频繁项,该事务的长度依旧大于事务最大事务限制长度,采取事务截断的方法进行处理。首先将项进行支持度从高到低排序,然后从最后一项开始截断,直到事务满足最大限制长度以后才停止阶段。这种方法虽然可以降低敏感度,但此方法必然会导致截断误差,项的支持度变小以后会影响频繁项集的生成从而导致结果的不准确。因此本文提出事务分离的方法,将长事务分离成多个短事务,避免了截断误差的产生。
2.1 基于指数机制的事务分离
在介绍基于指数机制的事务分离方法之前,首先说明项集与事务之间的距离的定义。
定义4 事务与项集之间的距离:现有事务T1和项集ci,则事务T1和项集ci之间的距离定义为
di=len(ci)-|T1∩ci|
(6)
其中,len(ci)为项集ci的长度,即ci中包含多少个项,而 |T1∩ci| 表示为项集ci事务T1中重复数据项的个数。
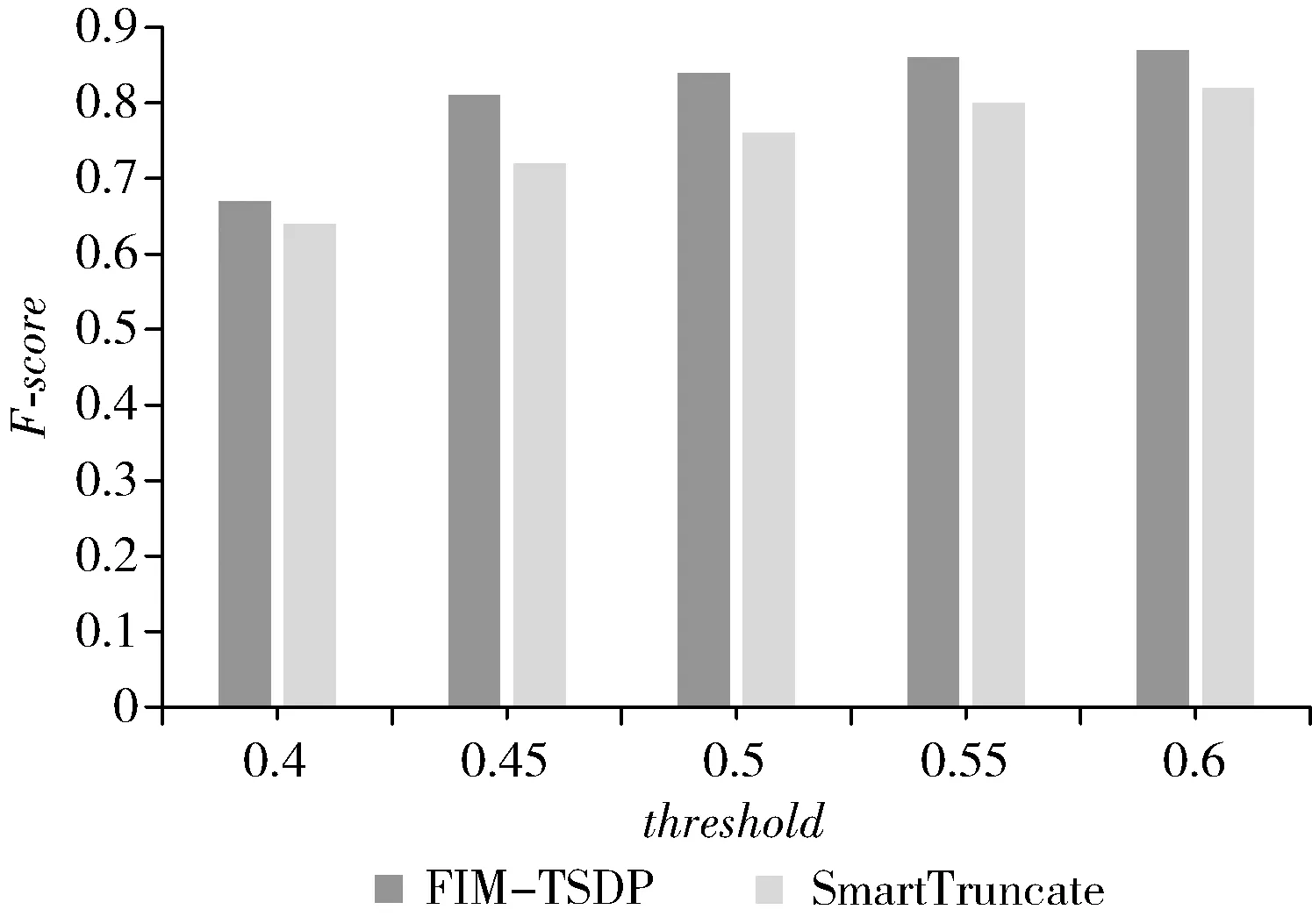
算法1采用差分隐私的指数机制来选择防止泄露事务数据集信息。设计质量函数q,进而对所有可能的事务长度进行打分,遍历最优限制比例S(S∈(0,1)), 求得当输出频繁项集可用性最高时S的值,然后通过指数机制进行选择事务最大限制长度。首先扫描数据集D中每条事务i的长度Zi及此条事务中最小支持度项Supzi。 将数据集D按照事务长度从小到大排序为D。然后根据指数机制设计质量函数q(D′,zi)。 当升序后的数据集长度和最优限制比例的乘积等于zj(j 由指数机制公式 (7) 其中,Δq为全局敏感度函数,其最大值为Supzi。 根据式(5)可知,长度zj为限制事务最大长度的概率为公式 (8) 基于指数机制的事务分离算法由算法1和算法2组成。 算法1:Exponential_length 输入:初始数据集D,隐私预算ε1,最优分离比例S 输出:最大限制事务长度L (1) Apriori(D)→候选1-频繁项集及其对应的支持度 (2) for每条事务i∈D (3) 按照事务长度zi降序排序 (4) 获取项最小支持度Supzi (5) end for (6) returnD′ (7) fori∈D′ (8) 设计质量函数 (10) end for (11) 根据Pr(L=zj)随机选择事务长度作为最大限制事务长度L 通过算法1得到最大限制事务长度L以后,进行长事务到短事务的分离。 算法2:事务分离 输入:事务T,候选项集Ci,事务最大限制长度L 输出:子事务集TM (1)TM→∅,Tm=∅ (2)C′i={ci&Ci&&ci∈T} (3) whileC′i≠∅ do (4) 随机选择ci添加入Tm并delci (5) while |Tm| (6)a=ci∩Tm (7)di=len(ci)-a (8) pickciwith minimum ofdifromC′ (9) if |ci∩Tm|≤Lthen (10) 将ci添加到Tm中; (11) end if (12) 从C′中删除ci (13) 将Tm添加到TM中 (14)m++ (15) end while (16) returnTM 具体描述在确定最大限制事务长度以后,将长事务t进行分离。首先挖掘频繁1-项集,进行长事务第一次分离,将不频繁项舍去,进而挖掘候选频繁2-项集,每次挖掘频繁项集时都对长事务进行一次分离。在挖掘出候选频繁k-项集以后,首先从包含于事务T的潜在频繁k-项集集合C中随机选择一个项集,添加进事务T1中;然后计算C中余下的每个Ci与T1之间的距离di。挑选出距离最小的Ci,并剔除Ci与T1中重复的数据项,将剩余的数据项添加进T1中。然后再将此步骤重复,循环往复的计算距离、剔除重复并添加数据项,直到将集合C中的数据项剔除完。在这个过程中,将距离最小的项添加进T1的同时要判断T1的长度,若大于最大限制长度则继续剔除,当等于最大限制长度的时候,建立T2,并且此事务长度为0,将Ci中剩余的项集重复计算距离、挑选最短距离的项、剔除重复项、这3个步骤,将数据项步骤添入事务T2中,完成对长事务的分离。 在拉普拉斯加噪过程中,由于拉普拉斯函数的特性,可能会产生正向和负向的噪声,因此当噪声过大的时候会产生支持度大于频繁(k-1)-项的k-频繁项,违背了Apriori频繁项集挖掘的先验定理。对于此问题,采取设置两个不同的支持度阈值的办法来解决。首先给定一个项集X的噪声支持度,分析该概率方式计算其在原始数据库中的支持度。第二步量化了加噪过程中的信息损失。假设在包含子项集X的不同事务之间存在均匀的分布。使用一个项集的平均信息损失来检查它是否频繁,以及使用最大的信息损失来确定是否使用它来生成候选项集。因此,鉴于有噪声的支持度,已经改变了阈值,以确定X是否频繁,以及是否使用X来生成(k+1)项集为用此方法放松这两个阈值。 给定k-项子集Y,Y的真实支持度计数用Rs表达、项集的噪声支持用Ns表达。 Pr(Rsi|Ns) 是用噪声支持度去估计真实支持度的条件概率 (9) 在加入噪声前,项集Y的真实支持度数值在加入噪声之前其分布可认为是在其值域内的均匀分布,即P(Rs1)=P(Rs2)=…P(Rsm)=1/m。 因此,上式可简化为 (10) 由于采用拉普拉斯机制,则 (11) 又Pr(Nc|Rcj) 积分值为1,由此可得 (12) 在加噪后,(k-1)-项集支持度小于k-项集支持度时,对两者的支持度进行修正,都将其降低或增加为两者的中值。用此方法对支持度进行调整以后,使其符合先验定理,提高了数据的可用性。 频繁k-项集挖掘算法如下: 算法3:频繁k-项集挖掘 输入:原始数据集D;隐私预算ε1、ε2;最小支持度阈值Supmin;(k-1)-项集集合Gk-1;事务最大限制长度L;最大事务长度限制比例S; 输出:频繁k-项集集合Fk;生成候选项集的项集集合Gk (1) 事务分离策略(D,Gk-1,S,ε1)→D′ (2) 通过Lk-1生成候选k-频繁项集Ck (3) for ∀k-项集 inD′ (4)Supk=Supk+Lap(CLk/ε1/k-1) (5) 当Supk≥Supmin时, 将此k-项集加入Fk (6) if存在Supk-1 (7)Supk=(Supk+Supk-1)/2,Supk-1=(Supk+Supk-1)/2 (9) 将k-项集加入Gk (10) end for (11) returnFk,Gk 由于支持度修正策略使用的数据为差分隐私保护后的带噪频繁项集及其支持度,根据差分隐私性质中的继承性,可知修正支持度后的算法满足ε-差分隐私。 为了检验基于指数机制的差分隐私频繁项集挖掘方法是否满足ε-差分隐私定义,需分别分析基于指数机制的限制事务最大长度计算方法和基于拉普拉斯机制添加噪声的方法是否满足ε1-差分隐私保护以及ε2-差分隐私保护。用FIM-TSDP表示本文提出的方法。 设M(D′) 是由长度升序排列后的数据集D′经过指数机制计算出的最大限制事务长度,此方法所分配的隐私预算为ε1,设D′和D″是邻近数据集。根据ε-定义可得 (13) 可得Pr(M(D′)=L)≤eε1×Pr(M(D″)=L)。 因此算法1满足ε1-差分隐私保护的定义。 下面验证加噪后的项集是否依然满足严格的数学定义 (14) D和D′为相邻数据集,YNs、Gk为Y的噪声支持度和真实支持度。又式 |YNs-YD′|-|YNs-YD|≤1。 因此条件概率比值可化简为 (15) 由此不等式可得,对支持度进行拉普拉斯加噪满足ε2-差分隐私保护。并且调整支持度是在加噪后的支持度上修正的,因此也满足差分隐私。可以验证FIM-TSDP满足ε-差分隐私保护。 本实验比较事务最大限制比例在不同事务数据集下对F-score的影响,以及算法FIM-TSDP和SmartTruncate在不同阈值下F-score和RE参数的对比。 F-score[16]为概括准确率和召回率关系的综合性能指标。准确率表示预测正确的个数占总预测结果的概率;召回率准确结果并且被挖掘出来的概率。两者间呈现负相关,为了平衡准确率和召回率的影响,使用F-score进行综合评判,即F-score越高,数据集可用性越好 (16) (17) (18) RE[16]则用于衡量算法输出结果中项集支持度与真实支持度间的相对误差。其定义为 (19) Y是差分隐私保护下生成的频繁项集,SupY是项Y的真实支持度,Sup′Y是项Y的噪声支持度。RE越小说明误差越小。 实验环境:Intel(R) Core(TM) i5-8265U CPU @ 1.60 GHz,4 GB内存,windows10 64位操作系统。采用python3.7语言进行实验。实验采用广泛应用于频繁项目集挖掘算法分析的数据集kosarak、retail和accident,表1总结了本实验中所用数据集的参数设置。 表1 数据集信息 为了说明事务最大限制长度对降低敏感度的有效性,实验采取了3个特点的数据集,由于差分隐私算法的随机性,实验对每组数据重复进行10次实验,并取其平均值。 设定k=100,总隐私预算ε=1.0,分析事务最大限制长度比例S取值不同时,分析不同S的取值对F-score以及RE的影响。 从图1可以看出,随着事务最大长度限制比例的增加,accident数据集F-score下降缓慢,是由于数据集随着S的变化,事务最大长度没有明显的变化。而当事务最大限制长度比例较小的时候,kosarak数据集和retail数据集F-score明显升高,说明了限制事务最大长度的方法有效降低了敏感度,提升了算法的可用性。 图1 S在不同事务数据集下对F-score的影响 由图2可知,在S=0.85时,3个点重合了,说明此时的总误差较小,数据集可用性较高。从而后续实验中都采取比例为0.85。并且从图中可以看出将kosarak数据集进行长度限制时,随着限制比例的变化,RE取值的变化最明显。这是由于此数据集中事务长度分布不均,比较分散。并且由于限制事务最大长度通过指数机制进行挑选,会导致S的取值稍有变化会明显影响RE。而accident与retail两个数据集中事务长度相对集中,因此无论事务最大长度限制比例怎样取值,经过指数机制挑选出的限制长度取值范围很有限,这使得RE变化相对很小。由此可知,S取值越小,误差越大,虽然全局敏感度更小了但是总误差变大了。并且从图1可知,随着当S大于0.85以后,会导致误差增大,增幅更快。由此可知,可推知分离误差对可用性的影响比噪音误差对可用性的影响更大。 图2 S在不同事务数据集下对RE的影响 图3~图8的隐私预算为1,它们显示了算法FIM-TSDP 的阈值从0.4到0.6下的F-score参数和RE参数的对比。 图3 数据集kosarak的F-score参数变化 图4 数据集kosarak的RE参数变化 图5 数据集accident的F-score参数变化 图6 数据集accident的RE参数变化 图7 数据集retail的F-score参数变化 图8 数据集retail的RE参数变化 由实验结果可以看出,在不同支持度阈值下,FIM-TSDP的F-score的参数值都高于SmartTruncate,RE参数值都小于算法SmartTruncate。 针对差分隐私在频繁项集中应用导致数据集可用性较差的问题,提出一种基于事务分离的差分隐私频繁项集挖掘算法FIM-TSDP。 在数据集预处理阶段,将超出事务最大限制长度的事务进行分离成多个子事务。在数据挖掘截断,在项集支持度上添加拉普拉斯噪声,并采用双阈值判断候选项集和频繁项集,以及支持度修正策略来减小添加噪声带来的误差,加强数据集的可用性。 最后,通过理论表明了该算法满足ε-差分隐私特性。将FIM-TSDP算法与SmartTruncate算法比较,通过实验验证了本算法有较高的可用性,但算法的时间复杂度还有待提高。

2.2 基于双阈值的频繁项集挖掘

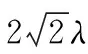

2.3 隐私分析
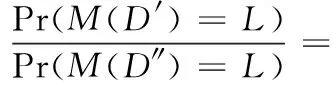

3 实验与分析
3.1 实验数据与设置

3.2 实验结果与分析







4 结束语

