基于模型预测的主动前轮转向与直接横摆力偶矩协同控制研究

李波 李双双 白艳飞 张国党 邵帅

（北京新能源汽车股份有限公司，北京 100176）

主题词：汽车动力学 侧向稳定性 模型预测 协同控制

1 前言

车辆动力学控制作为汽车底盘智能安全系统的重要保障，是高速自动驾驶的研究难点[1-3]。

Van Zanten 等较早提出了直接横摆力偶矩控制（Direct Yaw-moment Control，DYC）的概念[4]。而后，国内外学者围绕DYC扩稳理论及控制算法展开了大量研究。Li 等将汽车动力学状态划分为稳定、欠稳定、失稳临界及失稳等集合，促进了扩稳理论的应用及发展[5]。常见DYC 方法还包括模糊逻辑控制[6]及模型预测控制（Model Predictive Control，MPC）[7]等。Beal 等采用MPC算法将车辆运动约束于稳定区域内，实现了有限人为干预下的车辆稳定性控制[8]。尽管DYC 在临界失稳状态下具有较大干预潜能，但其会导致车辆部分动力性能暂时丧失。

除DYC 外，主动前轮转向（Active Front Steering，AFS）亦能通过修正前轮转角改善操纵稳定性[9]，其核心在于控制策略及算法设计，涉及反馈控制[10]、滑模控制（Sliding Mode Control，SMC）[11]、MPC[12]等方法。郭孔辉团队改进了线性时变MPC算法，仿真结果表明，改进算法可显著提高AFS横向动力学临界失稳阈值[13]。然而，当横向加速度过大、轮胎特性呈现较强的非线性特征时，AFS控制效能可能急剧恶化[14]。

DYC 及AFS 协同进行车辆稳定性控制有望发挥最优的横向动力学控制性能[15]。学者对非光滑最优控制[16]、鲁棒模糊控制[17]等在AFS及DYC协同控制器设计中的应用展开了研究。但是所述控制算法无法预测车辆运动状态和进行超前干预控制，因而实用性较差[18]。MPC能滚动预测并优化系统未来状态，已应用于DYC、AFS、制动能量回收等领域，但将其用于DYC 及AFS 协同控制中的研究仍不够充分。

基于此，本文针对汽车横向动力学稳定性控制问题，设计包含决策层和执行层的控制系统。上层采用MPC 方法获取预期附加横摆力偶矩，下层构建AFS 与DYC 协同控制策略对前轮转角及其制动压力进行分配。最后，通过仿真验证DYC-AFS 协同控制算法在中低附着路面工况下的有效性。

2 车辆动力学建模分析

选取质心作为车身坐标系原点，建立二自由度车辆模型如图1所示，其中OXY为大地参考系，Cxy为车辆参考系。

图1 二自由度车辆模型

假设转向过程中质心处纵向车速vx基本不变，根据力与力矩平衡定律，有：

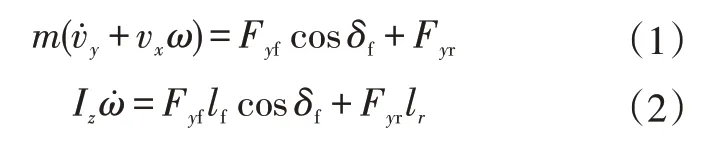
式中，m、Iz分别为整车整备质量和绕z轴转动惯量；lf、lr分别为质心与前、后轴的距离；δf为前轮转角；Fyf、Fyr分别为地面对前、后轮的侧向作用力；vy为质心处横向车速；ω为横摆角速度。

设路面附着系数为μ，当δf较小且车辆质心处侧向加速度小于0.5μg时，轮胎特性可近似认为处于线性区域[5]，满足关系：

式中，kf、kr分别为前、后轴侧偏刚度；αf、αr分别为前、后轮侧偏角；β为车身侧偏角。

注意到侧向车速与车身侧偏角满足关系：

由此可得车身侧偏角和横摆角速度的描述方程分别为：

在侧向加速度较小时，利用稳态回转工况下横摆角速度响应公式，可近似得到车身侧偏角和横摆角速度：

式中，l=lf+lr为整车轴距；K=m(lf/kr-lr/kf)/l2为稳定性因子。

考虑路面附着情况及系统时滞，在线性稳定的动力学区域内，车身侧偏角名义值βn及横摆角速度名义值ωn分别满足[19]：

式中，Tβ、Tω均为惯性时间常数；L-1()为反拉普拉斯（Laplace）变换算子；s为复变量；*表示卷积运算。

经验证，在线性稳定的车辆动力学工况下，式（7）和式（8）的计算结果与27自由度车辆模型基本吻合，能较好地反映驾驶员输入所期望的整车动力学关键状态[19]。

3 AFS与DYC协同控制器

3.1 控制器架构设计

基于MPC算法设计AFS与DYC协同控制器用于汽车横向动力学稳定性控制的核心思想在于：根据转向盘或前轮转角输入，获取能使车辆保持动力学稳定性的期望运动状态作为参考状态；为保持当前状态车辆稳定，基于决策层MPC 滚动优化得到所需附加横摆力偶矩，并输入执行层协调AFS 及DYC 子系统，进而修正前轮转角并分配各轮缸制动压力，实现修正整车横向动力学响应的目标。

控制系统决策层和执行层流程示意及各I/O接口参数或变量如图2所示。

图2 基于MPC的AFS及DYC协调控制系统决策层及执行层流程示意

3.2 决策层MPC算法

研究对象的描述方程式（5）、式（6）可进一步改写为状态空间表达式：

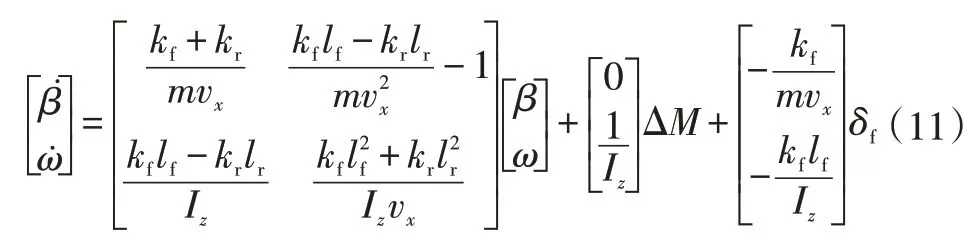
式中，ΔM为附加横摆力偶矩。

选取状态变量为x=(β,ω)T，控制变量为u=ΔM，式（11）可简写为：

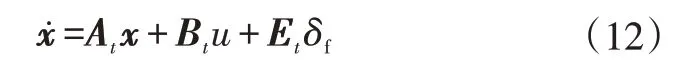
式中，At、Bt、Et分别为状态转移矩阵、控制矩阵和转角系数矩阵。

设参考状态变量为xr=(βr,ωr)T，βr为车身侧偏角参考值，ωr为横摆角速度参考值，参考控制变量为ur=ΔMr及参考前轮转角δf,r=δf，其中ΔMr为参考附加横摆力偶矩，令状态偏差为，控制偏差为，则式（12）转化为：

采用前向差分方法对式（13）离散化得：

式中，Ak=I+TAt为离散状态矩阵；Bk=TBt为离散控制矩阵；T为采样时间间隔。

式（14）即为被控系统的状态预测方程。

设预测时域和控制时域分别为Np和Nc，则决策层MPC算法的优化目标代价函数定义为：

式中，Q、R分别为状态和控制变量的权系数矩阵。

假设Np≥Nc，且Ak和Bk均为常矩阵（即Ak=A，Bk=B），则在预测时域Np内有状态转移方程：

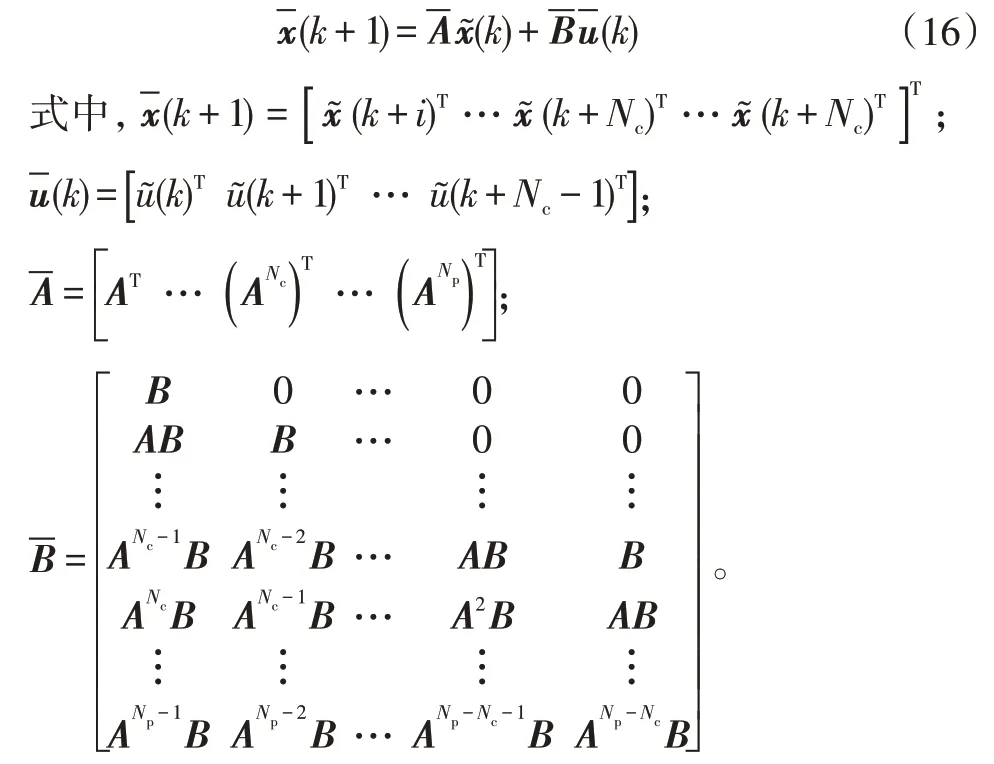
由式（15）和式（16）化简得到优化问题：

式中，umin和umax分别为控制变量u的最小值和最大值。

求解上述MPC滚动优化问题即可获得期望附加横摆力偶矩ΔM，以用于执行层协同控制。

3.3 执行层AFS与DYC协同算法

3.3.1 动力学稳定性判别准则

AFS 和DYC 均直接或间接地通过附加横摆力偶矩来控制车辆的行驶稳定性。AFS 对前轮转角的修正仅能在小范围内进行，对横向稳定性的干预控制有限。处于临界失稳状态时，DYC 应及时介入对各轮缸建压产生制动力，尽量维护车辆横摆动力学的稳定[14]。

据此，定义动力学稳定性因数为：

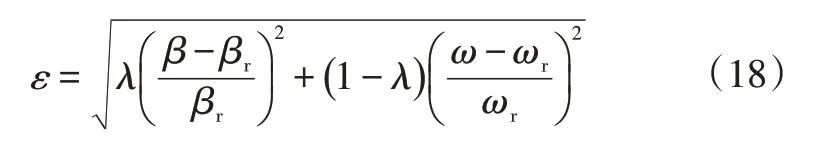
式中，λ为权重分配系数。

设由AFS 过渡到DYC 干预控制的阈值为εth：当ε≤εth时，所需附加横摆力偶矩主要由AFS 子系统执行层修正前轮转角产生；当ε＞εth时，DYC对车辆横向稳定性控制起主导作用，以实现及时反馈干预。转向过程中，当AFS和DYC触发附加横摆力偶矩时，忽略轮胎侧偏角，地面对汽车各轮作用力如图3所示。

图3 附加横摆力偶矩作用示意

3.3.2 AFS协同子系统

当决策层MPC 求解得到附加横摆力偶矩ΔM且ε≤εth时，由图3可知力矩计算关系：

式中，Fyfl、Fyfr、Fyrl、Fyrr分别为左前、右前、左后、右后轮受到的地面作用力；δfl、δfr分别为左前、右前轮转角；ΔMAFS为需由AFS子系统提供的附加横摆力偶矩。

假设道路曲率较小时满足δfl=δfr=δf,AFS，且两侧前轮及后轮的侧偏角分别近似相等：

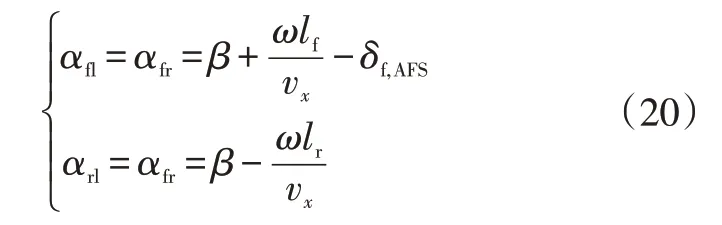
式中，δf,AFS为AFS触发时的总前轮转角。

考虑侧向加速度不太大的情形，各轮胎侧向力为：

式中，i=f,r 分别表示前、后轮，j=l,r 分别表示左、右轮；kij为相应轮胎的侧偏刚度，忽略垂向载荷转移的影响；αij为相应轮胎的侧偏角。

由式（18）～式（21）可得总前轮转角：

则AFS对前轮转角的修正量为：

3.3.3 DYC协同子系统

当ε＞εth时，决策层MPC 求解得到附加横摆力偶矩ΔM后，由图3可得：

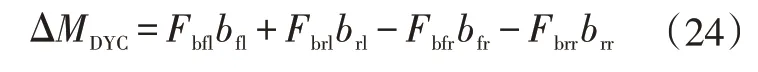
式中，Fbfl、Fbfr、Fbrl、Fbrr分别为由DYC 引起的地面对各轮胎作用力；bfl、bfr、brl、brr分别为各地面作用力对车辆质心的力臂。

当所需ΔMDYC＞0 时，优先对左后轮施加制动力矩，力矩不足时再对左前轮施加额外制动力矩，左侧轮胎作用力分配关系满足：

式中，hg为车辆质心距地面高度；Bf、Br分别为车辆前、后轴的轮距。

类似地，当ΔMDYC＜0 时，右侧轮胎作用力分配关系满足：

各轮缸压力与地面制动力满足关系：

式中，Kbij为相应车轮的制动力矩系数；pij为作用于相应车轮的制动压力；reij为相应车轮的滚动半径。

至此，得到轮缸压力。

4 结果分析及讨论

4.1 验证环境

采用CarSim 与MATLAB/Simulink 联合仿真方式验证本文基于MPC 的AFS 与DYC 协调控制算法，验证工况选为典型的低附着双移线（Double Lane Change，DLC）工况。所选车辆参数及路面条件如表1 所示，本文分别讨论路面附着系数为0.25 和0.40 时，车辆DLC工况下MPC策略对车辆动力学稳定性的控制效果。

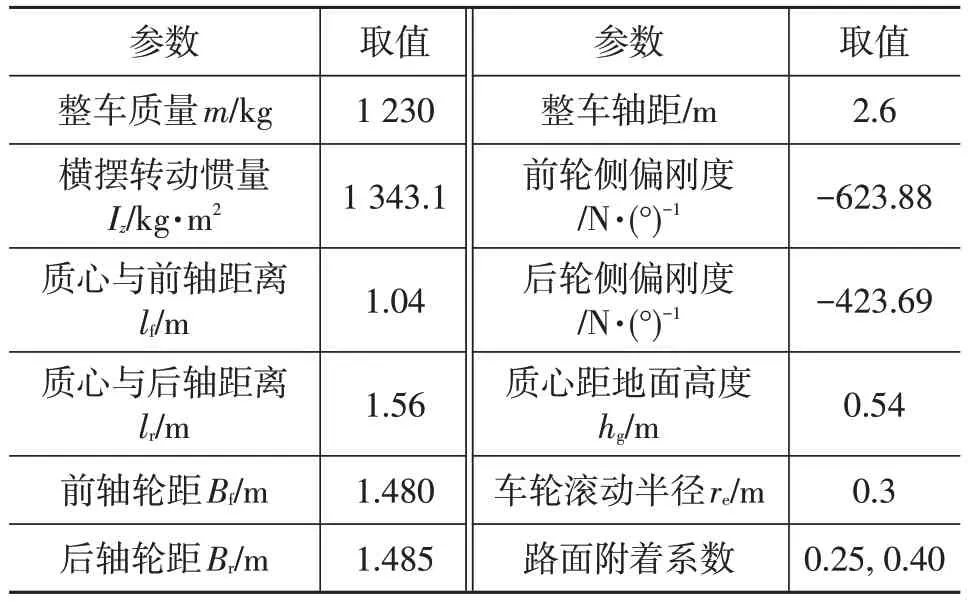
表1 车辆参数及道路条件

4.2 结果讨论

图4给出了采用与未采用MPC策略时车辆侧向加速度的变化趋势（路面附着为0.25）。可以看出，车辆行驶前6 s内，2种工况下的车辆侧向加速度基本吻合；而在第9～15 s 时间段内，侧向加速度最大值达到-6.07 m/s2，且最终未恢复至0附近，表明在DLC工况过程中车辆已失去横向稳定性。

图4 车辆侧向加速度变化情况对比（附着系数为0.25）

图5 和图6 分别给出了采用与未采用MPC 策略时车身侧偏角及横摆角速度的变化趋势（路面附着系数为0.25）。未采用MPC策略时，与图4对比可以看出：在第3～6 s时间段内车身侧偏角已超过15°、横摆角速度已低至-27.6(°)/s，车辆实际上已逐渐进入临界稳定状态；而在第6 s 后，车身侧偏角及横摆角速度变化率均急剧增加，表明车辆已经完全丧失了操纵稳定性。采用MPC策略加以控制后，在整个行驶时间内，车身侧偏角和横摆角速度分别稳定在-3.5°～3.5°与-16～16(°)/s 范围内，DLC工况下车辆横向稳定性得到明显改善。

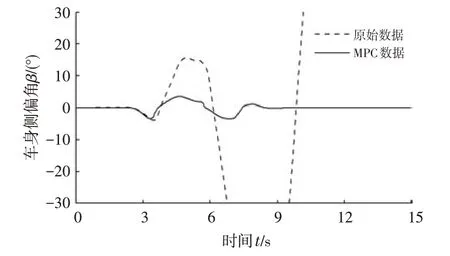
图5 车身侧偏角变化情况对比（附着系数为0.25）

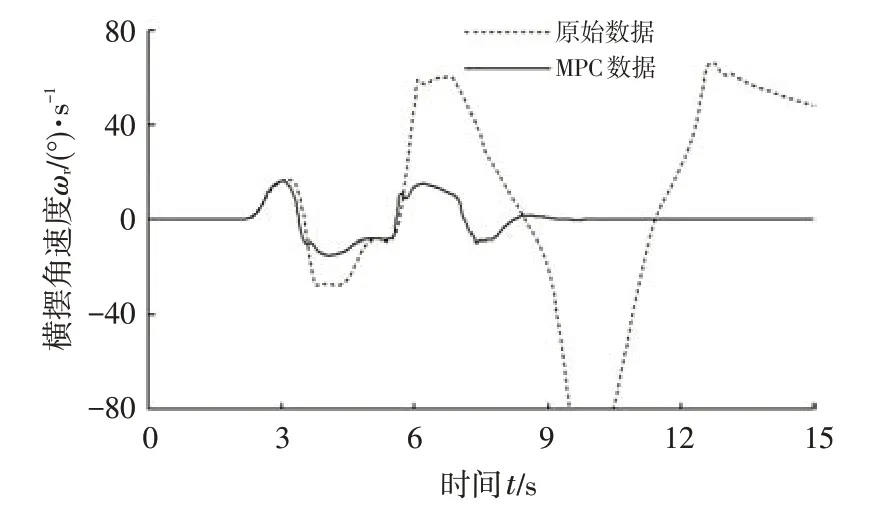
图6 横摆角速度变化情况对比（附着系数为0.25）

图7 给出了采用与未采用MPC 策略时车辆纵向速度的变化趋势（路面附着系数为0.25）。可以看出，未采用MPC策略时，在前6 s内，纵向车速由88 km/h缓慢降低而后急剧减小，尽管第10 s附近恢复至初始纵向车速的59.4%，但因为此时车身侧偏角和横摆角速度变化率过大，车辆已经丧失操纵稳定性，所以纵向车速骤降至0附近。采用MPC策略后，车辆纵向车速基本稳定于初始速度88 km/h 附近，这表明该控制策略有助于提高车辆在DLC工况下的操纵稳定性。

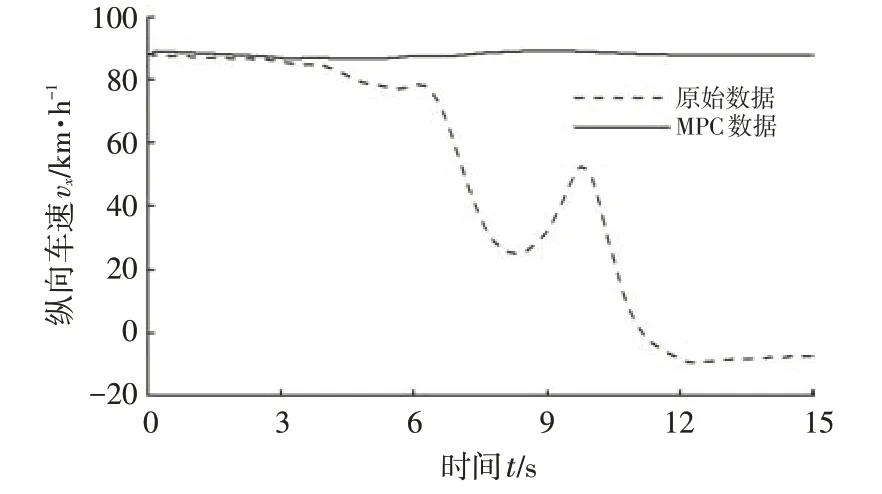
图7 车辆纵向速度变化情况对比（附着系数为0.25）

图8 和图9 分别给出了车辆纵向速度和侧向加速度、横摆角速度和车身侧偏角的对比曲线（路面附着系数为0.40）。由图8、图9可见，未采用MPC策略时，车辆在DLC 工况下约第5 s 以后纵向速度出现衰减波动，约第6 s 后加速度出现急剧波动，横摆角速度和车身侧偏角均出现了渐扩振荡，且随时间推移，振荡幅度进一步增大。采用MPC策略后，纵向车速可维持在90 km/h附近，侧向加速度可保持在0 附近，车辆横摆角速度和车身侧偏角分别稳定于-25～25(°)/s 和-2.5°～2.5°范围内，侧向稳定性得到明显改善。

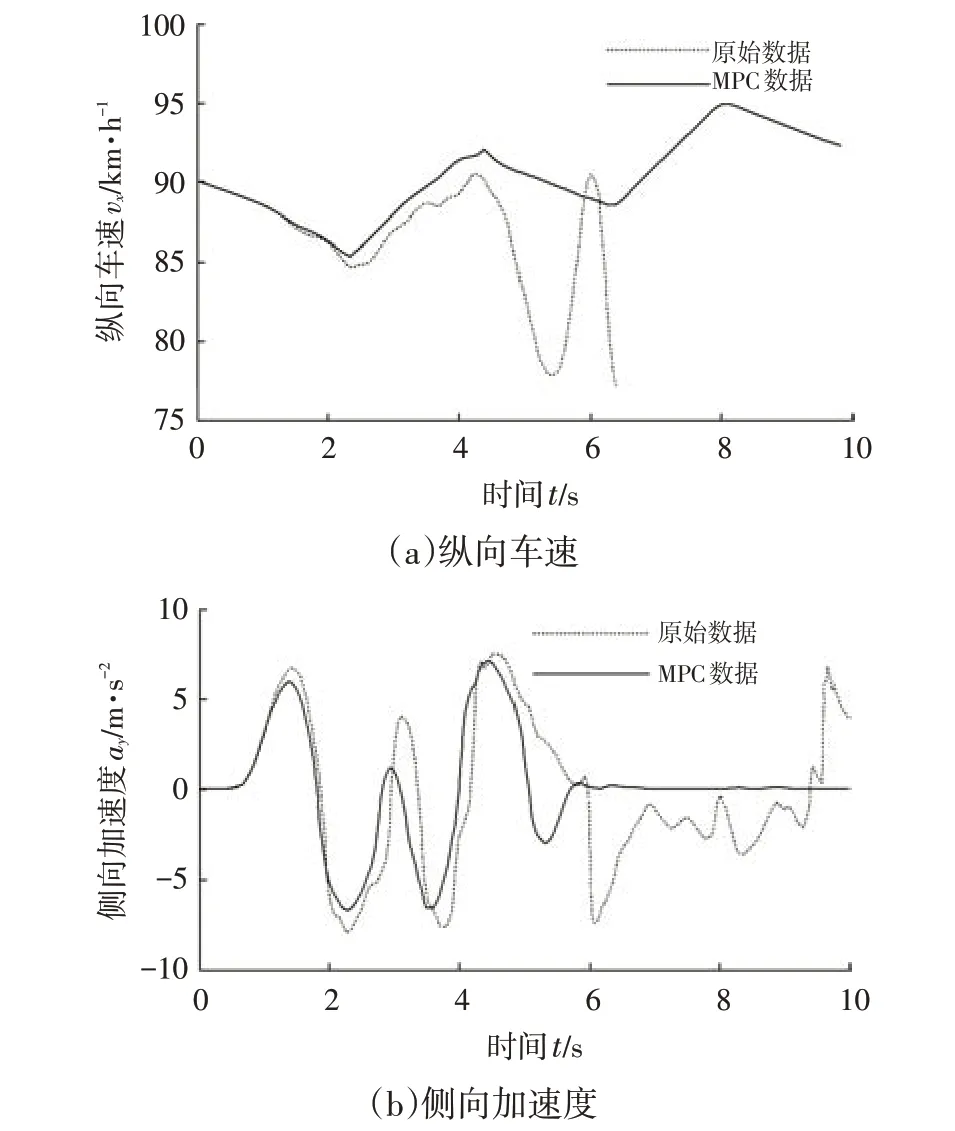
图8 车辆纵向速度和侧向加速度对比（附着系数为0.40）

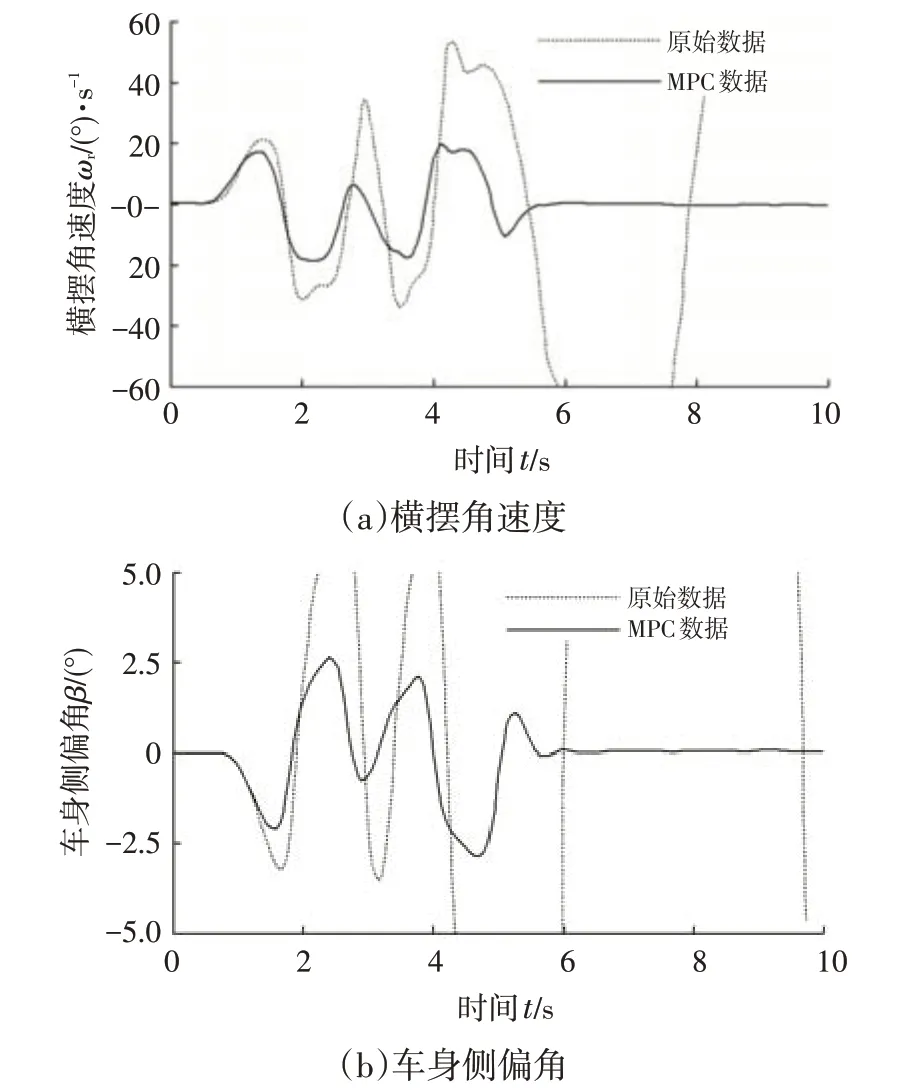
图9 横摆角速度和车身侧偏角对比（附着系数为0.40）

图10 给出了车辆行驶轨迹的对比曲线（路面附着系数为0.40）。可以看出，采用MPC 策略后，车辆在纵向距离100 m 和155 m 附近的侧向偏差分别减少37.5%和41.8%，实际行驶路径基本符合期望轨迹，表明该协同控制策略可明显改善车辆的动力学稳定性。

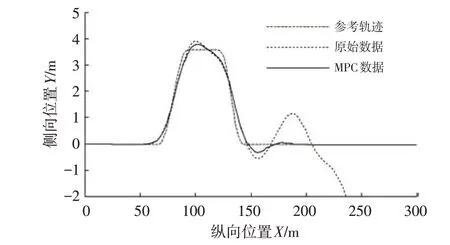
图10 车辆行驶轨迹对比（附着系数为0.40）

5 结束语

本文针对车辆侧向动力学稳定性控制问题，构建了基于MPC 的双层AFS 与DYC 协同控制器，决策层采用MPC 算法优化获得附加横摆力偶矩，执行层根据所优化的横摆力偶矩，采用AFS 与DYC 协调控制分配前轮附加转角或各轮缸制动压力，最后基于CarSim 和MATLAB/Simulink 联合仿真验证了该协同控制器在路面附着系数为0.25及0.40条件下的控制效果。

结果表明：在中低附着系数路面条件下，与无控制时对比，基于MPC的AFS-DYC 双层协调控制器可有效保持车辆DLC 工况下纵向车速不降低，并将车身侧偏角和横摆角速度抑制于稳定行驶范围内，进而减小行驶轨迹的横向偏差，因此该控制器可显著改善车辆操纵稳定性，明显提升横向动力学稳定性，最终抑制车辆由临界失稳态进入不可控的失稳态。