基于运行数据的公交客车动力系统参数优化*

赖辉平 郑正中 王少杰 侯亮 苏亮

（1.厦门大学，厦门 361104；2.厦门金龙联合汽车工业有限公司，厦门 361023）

主题词：动力系统参数优化 乘客人数 运行工况构建 最优拉丁超立方设计 混合动力客车

1 前言

随着网络、感测技术的进步，获取复杂装备的运行数据成为可能，将运行数据反馈至研发设计前端对提高产品性能具有重要意义[1]。传统优化设计大多在理想环境下进行，但复杂装备的实际运行环境会导致产品的真实输出与预期存在较大偏差[2]。

混合动力公交客车作为复杂装备产品，其动力系统的参数设置直接影响整车节油潜能，但制造商在产品设计中进行参数初选时一般侧重于满足车辆的动力性指标，容易忽略其对整车经济性的影响[3]。因此，在控制策略确定以及驾驶风格固定的基础上对混合动力系统参数进行优化设计尤为重要。He 等[4]将多岛遗传算法和序列二次规划算法相组合，建立了动力总成参数优化模型，得到了混合动力系统的最优部件组合方案。Zheng等[5]定义了由制造成本和能耗组成的目标，通过数据处理得到可反映公交车实际运行特点的工况，基于遗传算法得到了客车关键部件最优参数。曾小华等[6]通过多岛遗传算法对行星排特征参数和控制策略参数进行优化分析，提高了车辆的燃油经济性。Yildiz 等[7]在满足关键性能要求的基础上，结合粒子群优化（Particle Swarm Optimization，PSO）算法实现了混合动力汽车的动力部件优化设计。对于城市公交客车，其运营过程中工况和整车质量直接影响车辆的燃油经济性，但鲜有研究考虑瞬时整车质量对参数优化结果的影响。在实际运营中，乘客人数会随公交站点的上、下客情况发生改变，使得整车质量变化，若在动力系统参数优化时将整车质量设为定值，可能无法充分发挥混合动力系统的节能潜力。同时，基于标准工况对动力系统参数进行优化可能使得在真实运营环境下燃油经济性的改善效果与预期相差较大。

为此，本文将运行数据反馈至设计前端，提出运行数据驱动的混合动力客车动力系统参数优化方法。首先通过车联网运行数据构造具有代表性且符合实际特点的行驶工况，代替中国典型城市公交工况；其次，利用基于最优拉丁超立方设计的混合动力客车动力系统参数双层优化模型代替假设的固定载荷；最终，在满足动力性要求的基础上，充分发掘动力系统的节能潜力，验证所提出方法的有效性。

2 混合动力客车动力系统参数优化方法

产品在役运行数据相对于标准或试验数据在数据来源、数据分析目的、工况以及外部环境等因素上存在较大差异，通过对产品运行数据的挖掘分析，实现产品的优化设计，可以更好地满足实际需求[8]。本文给出运行数据驱动的混合动力客车动力系统参数优化方法的一般流程，如图1所示。

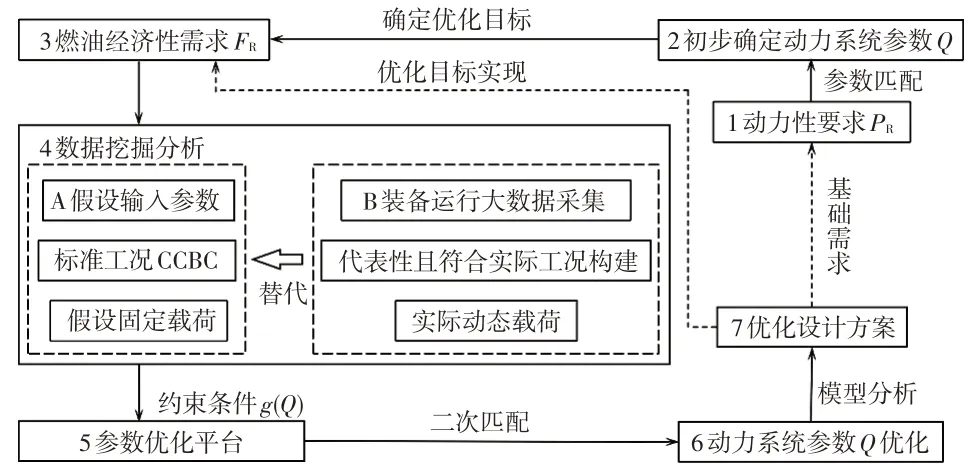
图1 运行数据驱动的混合动力客车动力系统参数优化方法

其中，传统客车优化设计的过程为：通过极限加速工况、爬坡工况和最高巡航速度工况等指标性参数匹配，选择满足基础动力性要求（Power Requirement，PR）的动力系统参数Q，在此基础上构建燃油经济性需求函数（Fuel economy Requirement，FR），搭建全局参数优化平台，并假设输入参数，包括中国典型城市公交工况（China City Bus Condition，CCBC）和固定载荷，结合MATLAB/Simulink 整车动力系统参数确定优化设计方案。传统优化设计未充分考虑城市实际运行工况以及乘客人数改变对动力系统优化设计的影响，由此导致客车的实际使用性能低于预期设计性能。然而，实际运行工况与标准工况相比，加、减速更为频繁，乘客人数也会发生明显改变。

车辆纵向动力学模型为：

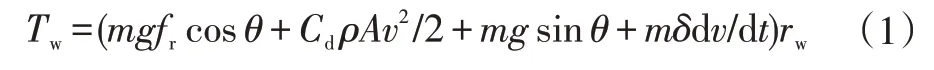
式中，Tw为车轮转矩；m为整车质量；fr为滚动阻力系数；g为重力加速度；θ为坡度；Cd为空气阻力系数；A为迎风面积；v为车速；δ为旋转质量换算系数；rw为轮胎半径；ρ为空气密度。

因此，充分考虑运行过程中工况和瞬时整车质量的影响对有效发挥动力系统节能潜力尤为重要。以插电式混合动力客车（Plug-in Hybrid Electric Bus，PHEB）动力系统参数优化设计为例，本文基于运行数据驱动的混合动力客车动力系统参数优化方法的框架设计参数优化模型，如图2 所示。获取车联网运行数据，构造具有代表性且符合实际行驶特点的某市城市公交客车工况并搭建基于最优拉丁超立方设计（Optimal Latin Hypercube Design，Opt-LHD）的混合动力客车动力系统参数双层优化模型，分别代替标准工况和假设的固定载荷。以公交站点位置为划分依据，利用核主成分分析（Kernel Principal Component Analysis，KPCA）和PSO K均值聚类算法得到具有代表性且符合实际运行特点的某市城市公交客车工况，将其作为输入工况。利用混合动力客车动力系统参数双层优化模型内层的Opt-LHD产生试验矩阵，即乘客人数，根据所构建的城市公交客车工况站点分布，转换试验矩阵为整车载荷时间序列，并将其与MATLAB/Simulink 整车模型和发动机最优控制策略相结合，以试验矩阵等效燃油消耗量均值的最小值为目标函数，等效燃油消耗量为：

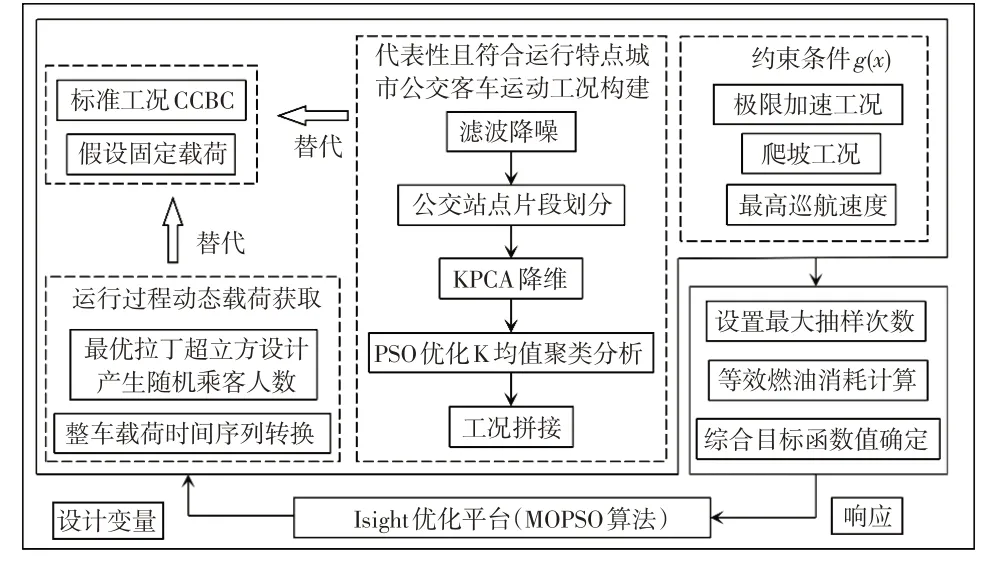
图2 PHEB动力系统参数优化模型

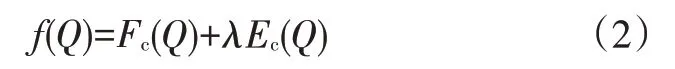
式中，Fc(Q)为燃油消耗量；Ec(Q)为电耗；λ为等效燃油系数。

本文的双层优化模型在Isight软件中搭建，通过试验设计（Design Of Experiments，DOE）、计算器、MATLAB以及优化模块实现，在优化模块中选择多目标粒子群算法（Multi-Objective Particle Swarm Optimization，MOPSO）作为外层算法，利用Bat批处理文件实现模型的调用。

3 城市公交客车行驶工况构建

3.1 数据获取与预处理

通过车联网平台获取大量的线路运行数据，以公交站点的位置作为行驶片段划分依据，搭建城市公交客车行驶片段数据库。由于城市公交客车运行过程复杂多变，本文利用数字滤波算法对行驶片段数据库进行去噪和平滑。为尽可能反映每个行驶片段的特征，选取8个特征参数构造特征参数矩阵[9]，如表1所示。

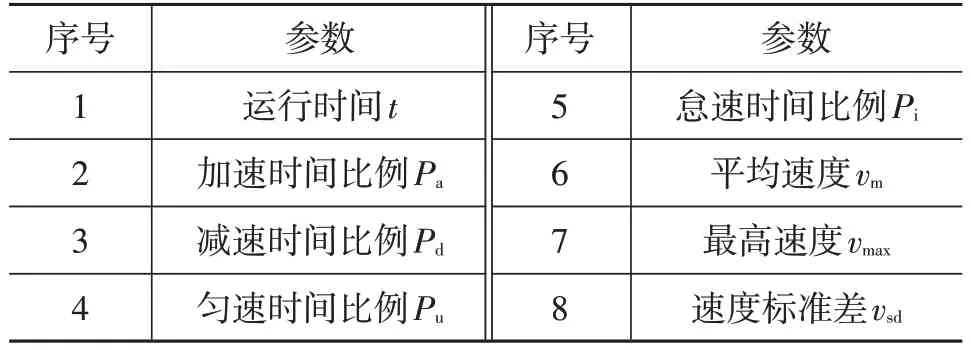
表1 反映行驶片段的典型特征参数

为消除不同量纲的影响，对特征参数矩阵进行标准化处理：

式中，aij、bij分别为标准化处理前、后第i个样本的第j个变量；E(ai)、D(ai)分别为标准化处理前第i个样本对应的均值和方差。

3.2 核主成分分析特征参数降维

为减少特征参数间相互干扰导致的信息重叠，本文采用KPCA进行特征参数降维，通过主成分信息来反映城市公交客车行驶片段的大部分特征，将特征参数矩阵转换为主成分信息。通过非线性映射将非线性可分的原始样本输入空间变换到一个线性可分的高维特征空间，然后在新的空间中完成主成分分析[10]。

首先对样本数据Xi进行非线性转变δ(Xi)，由此得到原始数据的协方差矩阵C：

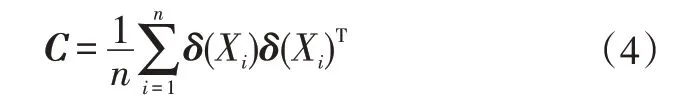
式中，n为样本数量。

此时引入非线性函数δ(Xk)，特征值μ和协方差矩阵的特征向量V满足以下关系：

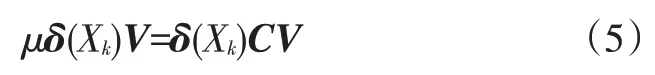
使得特征向量V能够由非线性函数表示为：

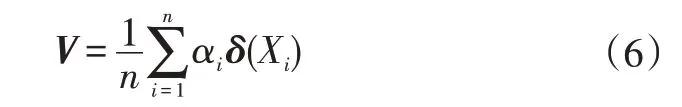
式中，αi为常数。

再引入核函数L=δ(Xk)δ(Xj)，将式（6）代入式（5），可以得到：

式中，α为核函数矩阵L的特征向量。

同时对其进行中心化处理，得到处理后的核函数：

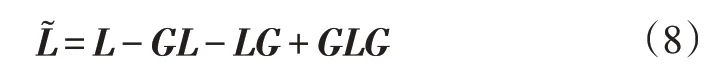
式中，G为n阶方阵。

对行驶片段的特征参数矩阵进行核主成分分析得到各主成分及其对应的累积贡献率，如表2 所示。前4个主成分的累积贡献率超过85%，同时主成分方差大于1[11]，即前4个主成分代表了行驶片段的大部分信息，故以对应的主成分得分矩阵作为后续聚类分析的输入数据。

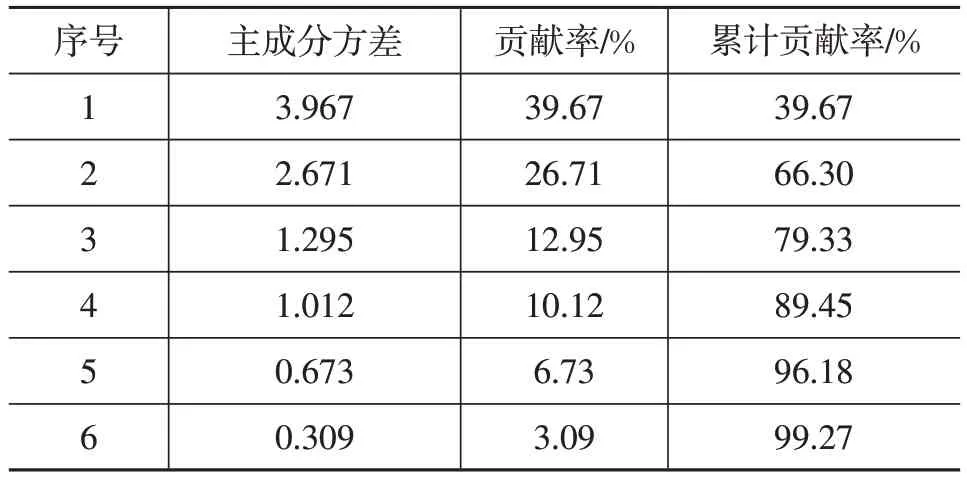
表2 主成分方差及贡献率

3.3 粒子群优化K均值聚类分析

K 均值聚类分析根据欧式距离将样本分配至不同的类中心，具有类内相似度高、类间相似度低的特点[12]。对核主成分分析得到的4 个主成分进行聚类分析时，由于传统的K 均值聚类容易陷入局部最优解，故利用全局寻优能力优秀的PSO 算法获得最优的聚类结果。PSO 算法[13]中粒子的速度和位置的更新过程为：

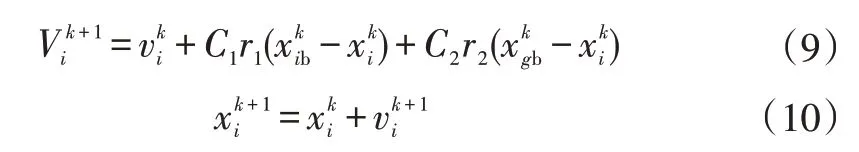
根据城市公交客车的行驶特点以及观察不同分类数目的聚类效果后，设置聚类数目为3[14]，由此得到3类行驶片段的样本集，并对其进行相关性分析：

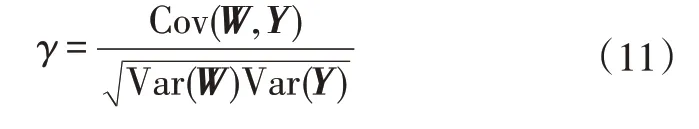
式中，vik、xik分别为第i个粒子第k次迭代的速度和位置；分别为第k次迭代时，第i个粒子的最佳位置和全局群的最佳位置；C1、C2分别为学习因子；r1、r2分别为随机生成的0～1范围内的实数；γ为相关系数；W为各主成分得分矩阵；Y为综合特征；Cov(W,Y)为W和Y的协方差；Var(W)、Var(Y)分别为W和Y的方差。

根据某市城市公交客车的站点实际平均设置情况，本文设置29个公交站点即28个行驶片段。将每类行驶片段样本对应的相关系数由大到小排列，按照3类样本集的比例大小依次进行拼接，构建具有代表性的某市城市公交客车行驶工况（Representative Bus Condition，RBC），如图3所示。其特征参数与标准工况CCBC和车联网实际采集数据的对比结果如表3所示，CCBC如图4所示。

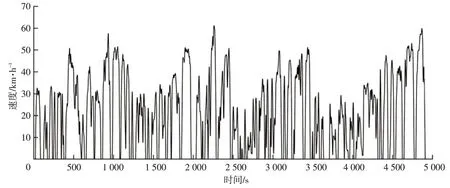
图3 某市城市公交客车行驶工况

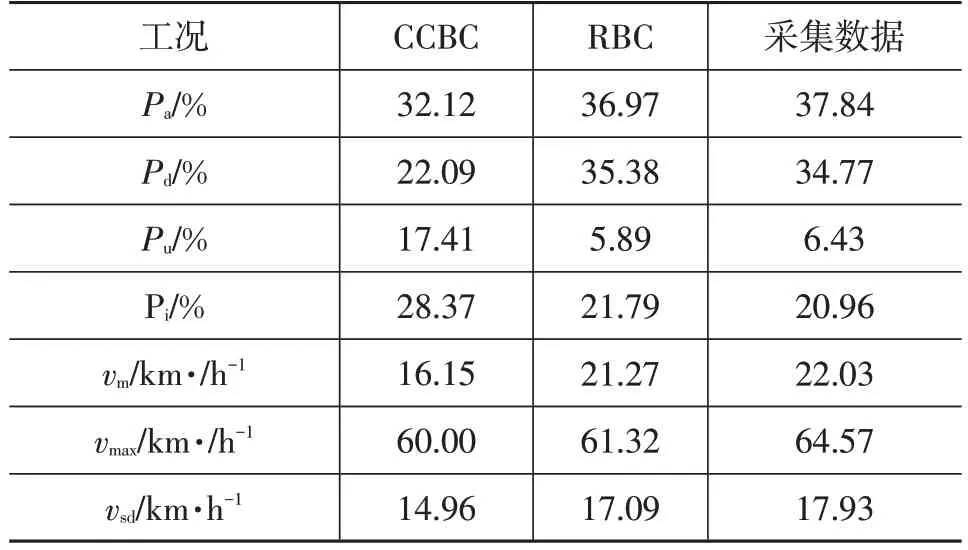
表3 RBC与CCBC及实际采集数据特征参数对比

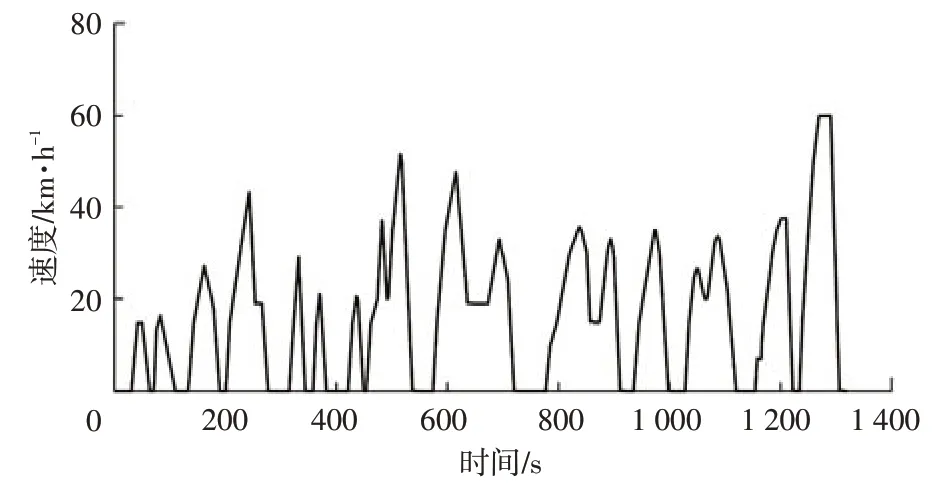
图4 CCBC标准行驶工况

可以发现，标准工况CCBC的各项特征参数与车联网实际采集数据有较大差异，所构建的RBC的加、减速变化情况较标准工况CCBC 更为频繁且RBC 的特征参数与实际采集数据相差较小。所构建的RBC各项特征参数与实际采集数据的相对误差分别为2.30%、1.75%、8.40%、3.93%、3.45%、4.96%和4.68%，均小于10%，说明所构建的RBC 能够真实反映道路的运行状况，具有代表性，较标准工况CCBC 更能充分、真实地体现该市城市公交客车的运行特征，因此将RBC 代替假设输入标准工况CCBC。

4 基于Opt-LHD的动力系统参数优化

4.1 优化模型搭建

在城市公交客车实际运营过程中，乘客人数随机变化，由此可能导致基于固定整车质量的动力系统参数优化得到的结果只为特定整车质量下的最优解，为了寻找不同整车质量下最优的混合动力系统参数，本文建立基于最优拉丁超立方设计的混合动力客车动力系统参数双层优化模型，用最优拉丁超立方设计产生运行过程中的动态载荷来代替假设的固定整车质量。其流程如图5所示，设计流程如下：

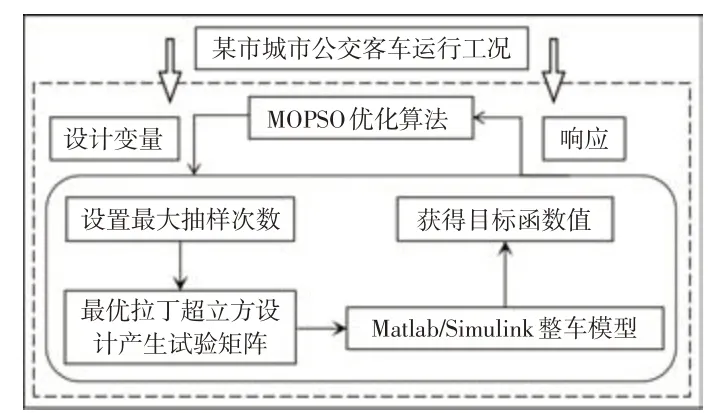
图5 双层优化模型设计流程

a.将构建的某市城市公交客车行驶工况作为目标工况，输入至MATLAB/Simulink整车模型；

b.基于外层的MOPSO 算法，在设计空间内提供控制因子传递至内层进行迭代；

c.通过内层的最优拉丁超立方设计实现乘客人数的随机产生，生成试验矩阵，并将其转换为整车质量时间序列；

d.将整车质量时间序列与MATLAB/Simulink 整车模型和发动机最优控制策略相结合，进行仿真分析，获得燃油消耗量结果，并把试验矩阵的均值作为优化的目标函数值；

e.内层产生响应传递至外层MOPSO 算法，求解目标函数最小值，若达到迭代次数上限，停止优化分析；反之，重复步骤b～e，直至到达停止条件。

以上流程在Isight 软件中实现，利用Bat 批处理文件实现各模块的串联，其平台设计如图6 所示。其中MOPSO算法是在PSO算法的基础上引入经验集策略实现的[15]。

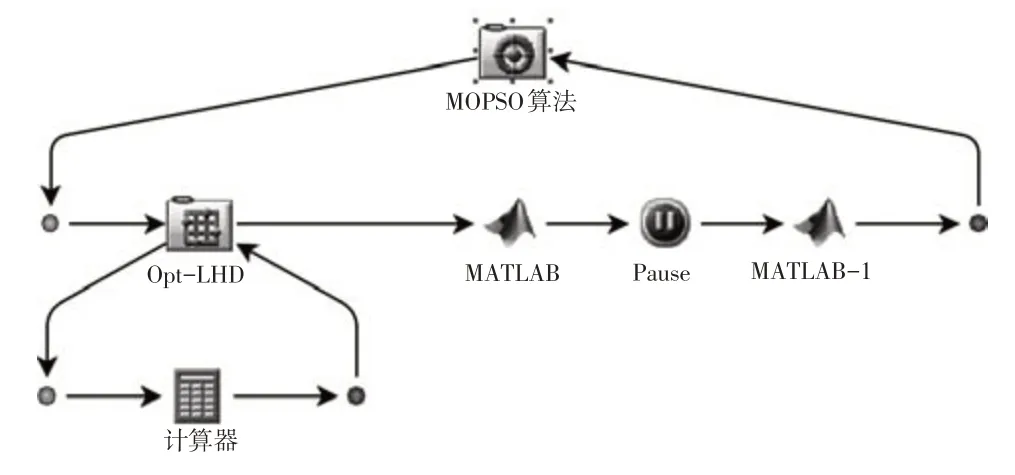
图6 双层优化模型Isight实现

4.2 功率分流式混合动力系统建模

基于传统的单行星排混合动力系统确定研究构型，结构如图7 所示，该系统包括行星排、发动机、电机MG1、电机MG2、离合器CL1、离合器CL2和固定速比减速器。

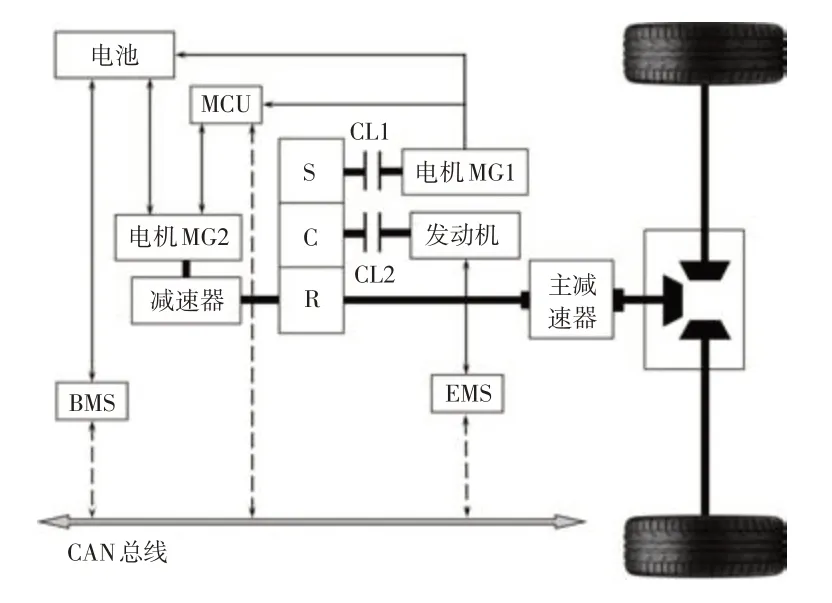
图7 混合动力系统构型

其中电机MG1和发动机分别通过离合器CL1和离合器CL2与行星排的太阳轮S和行星架C相连接，电机MG2 经过固定速比减速器连接行星排的齿圈R 和动力输出端，通过行星排的转速、转矩双解耦实现发动机和电机的共同驱动。利用离合器CL1的断开，实现双电机驱动，同时可以防止高速巡航时出现功率循环现象，通过离合器CL2 的断开可以增大纯电动的驱动范围。电机MG2 处的固定减速器能够有效防止高速时电机转速过高。根据城市公交客车的动力性能要求进行参数匹配，初步确定动力系统参数，如表4 所示。利用MATLAB/Simulink 建立PHEB 整车模型，包含发动机模型、电机模型、电池模型、行星排模型、车辆动力学模型、驾驶员模型和控制策略模型。

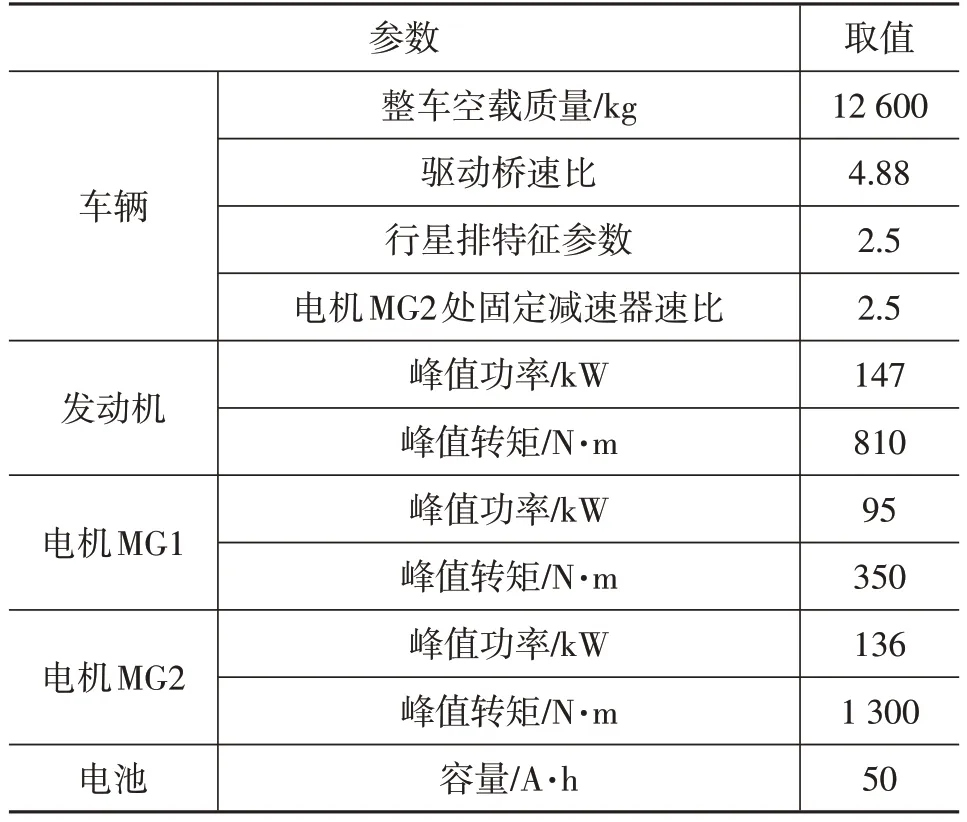
表4 动力系统计算参数

发动机模型和电机模型均采用试验建模法，通过发动机燃油消耗率和发动机转速与转矩MAP图描述发动机的动态特性。发动机燃油消耗率fe为：

式中，Te为发动机转矩；ne为发动机转速。

忽略动态特性和热交换过程对电机效率的影响，通过电机转速、转矩查表得到电机效率，电机的功率Pm为：

式中，Tm为电机转矩；ωm为电机转速；ηm为插值查表得到的电机效率。

电池的基本物理模型由一个具有单一内阻的静态等效电路推导得到，根据基尔霍夫定律得到电池荷电状态（State Of Charge，SOC）与电池电流的关系：

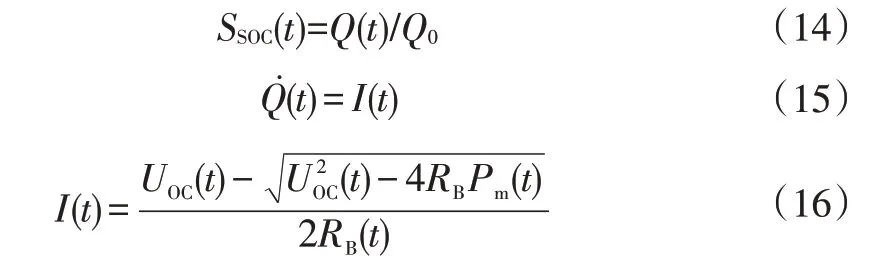
式中，SSOC(t)为当前时刻电池荷电状态；Q0、Q(t)分别为电池的初始容量和t时刻的电池容量；I(t)为电池电流；UOC(t)、RB分别为开路电压和电池内阻。

根据静力学关系和行星排内部转速、转矩关系建立行星排模型，输出轴的转矩、转速关系为：

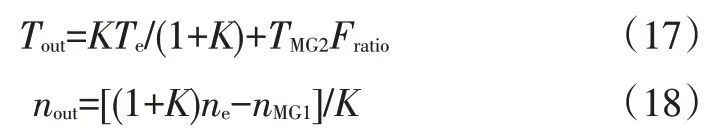
式中，K为行星排特征参数；Fratio为电机MG2处固定减速器速比；nMG1为电机MG1 的转速；Tout为输出轴转矩；nout为输出轴转速；TMG2为电机MG2的转矩。

结合输出轴转矩和车轮端速度搭建如式（1）所示的纵向动力学模型，驱动阻力由滚动阻力、空气阻力、坡度阻力和加速阻力构成。

采用发动机最优控制策略实现功率分流式混合动力系统的整体控制，将发动机控制在其最优工作区间，具有良好的实时性和鲁棒性[16]。根据不同功率需求，驱动模式可分为单电机驱动、双电机驱动和混合动力驱动模式，依据电池SOC和当前车速将制动模式分为机械制动和再生制动。

4.3 仿真分析

混合动力系统的参数设置直接影响整车的节油潜能，初选时侧重于满足城市公交客车的动力需求，忽略了其对经济性的影响。同时，混合动力系统的主要参数选择范围较大，说明混合动力客车动力系统参数还存在很大的优化空间。本文选择行星排特征参数和电机MG2 处固定减速器速比作为优化变量，以极限加速工况、爬坡工况和最高巡航速度工况作为约束条件，综合确定优化变量的取值分别为2.30～2.70和2.50～3.02。在城市公交客车实际运营过程中，乘客人数是随机变化的，无法通过车联网数据进行准确预测，因此将不同行驶片段的随机乘客人数作为噪声因子，采用最优拉丁超立方设计对噪声因子的设计空间进行采样，充分模拟在运行过程中可能出现的人数情况，设置最大乘客人数为60人，假设每位乘客的质量为70 kg，将其与城市公交客车空载质量相加即为运行过程中整车的质量：

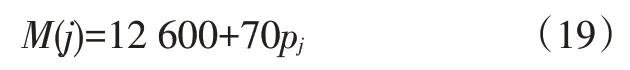
式中，M(j)为第j个公交站点后的整车质量；pj为第j个公交站点片段的乘客人数。

最优拉丁超立方设计改进了随机拉丁超立方设计的均匀性，并且在解决空间填充问题上具有更优的性能[17]。设置最优拉丁超立方设计的试验次数和最大迭代次数分别为100 次和300 次，即产生100 组整车质量时间序列和28×100的试验矩阵。按照设计步骤进行双层优化，行星排特征参数和电机MG2 处固定减速器速比的优化迭代过程如图8、图9所示，优化后的行星排特征参数和电机MG2 处减速器减速比分别为2.59 和2.83。

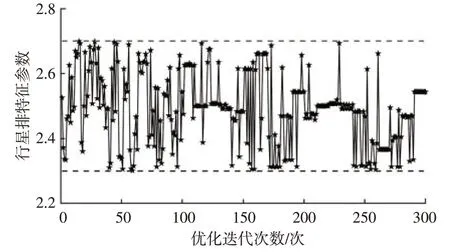
图8 基于Opt-LHD的行星排特征参数优化过程

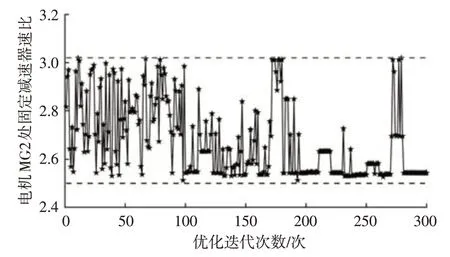
图9 基于Opt-LHD的MG2处固定减速器速比优化过程

4.4 优化结果分析

为了评估所提出方法的效果，验证基于最优拉丁超立方设计的动力系统参数双层优化模型对燃油经济性的改善水平，选择基于固定整车质量动力系统参数优化方法即未考虑乘客人数随机变化的优化方法和优化前的参数进行对比分析，结果分析的流程如图10所示，分别为建立基于固定整车质量的动力系统参数优化前的结果分析模型、基于固定整车质量的动力系统参数优化后的结果分析模型和基于最优拉丁超立方设计的结果分析。

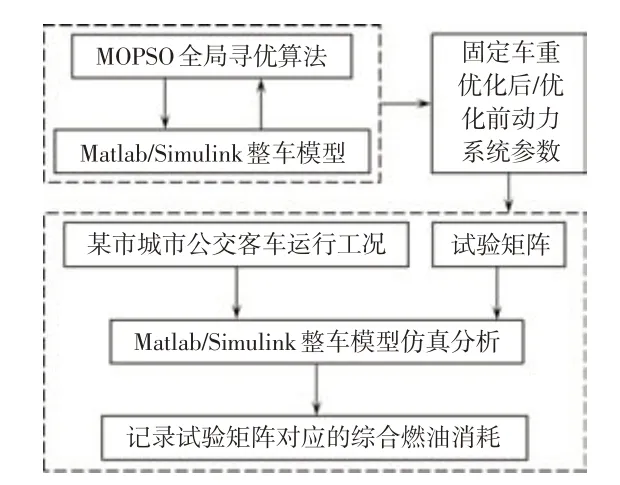
图10 结果分析流程

设置固定整车质量为14 000 kg，即乘客人数取20人，设置优化迭代次数为300 次，利用MOPSO 算法对PHEB的动力系统参数进行全局寻优，将优化后的结果输入至MATLAB/Simulink整车模型进行仿真验证，与最优拉丁超立方设计产生的试验矩阵相结合，仿真得到100 km燃油消耗量结果并计算其均值。每次迭代的对比结果如表5 所示，300 组试验矩阵对应的燃油消耗量均值的对比结果如表6 所示，可以发现，经基于最优拉丁超立方设计的动力系统参数双层优化模型优化后的100 km燃油消耗量均值较基于固定整车质量和优化前分别减少了1.47 L 和1.98 L，说明该模型能够有效提高燃油经济性，较传统不考虑随机乘客人数变化的优化方法更能发挥动力系统节能潜力，能够反映产品实际使用环境下的需求。

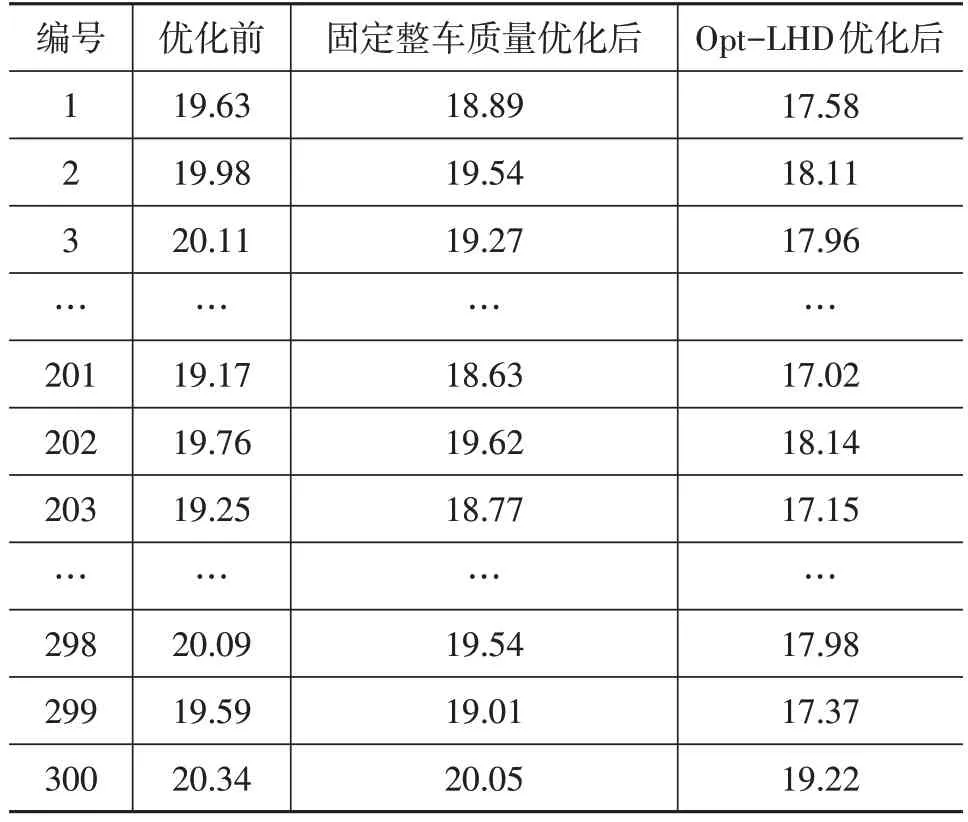
表5 试验矩阵100 km燃油消耗量结果 L

表6 300组试验矩阵燃油消耗量均值对比

为说明动力性满足情况和电池SOC的变化情况，以最优拉丁超立方设计产生的一个动态质量时间序列为例，经基于最优拉丁超立方设计的混合动力客车动力系统参数双层优化模型优化后的电池SOC 变化情况和车速跟随效果如图11、图12所示，实际车速和目标车速的均方根误差（Root Mean Squared Error，RMSE）为：

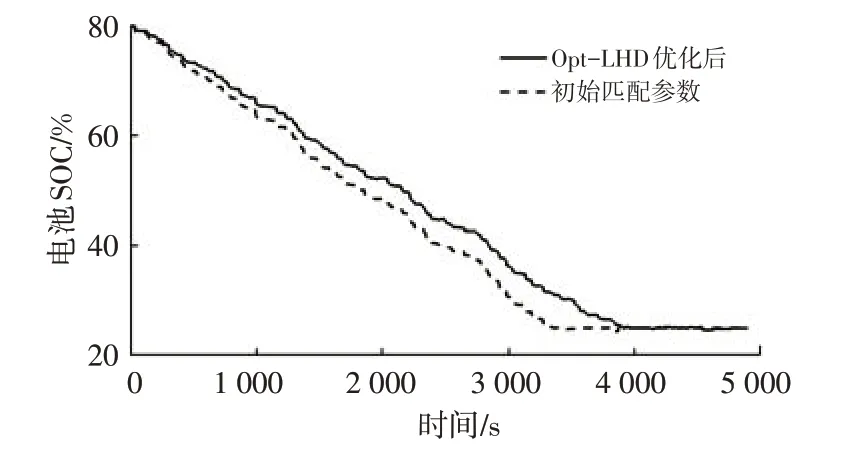
图11 电池SOC对比

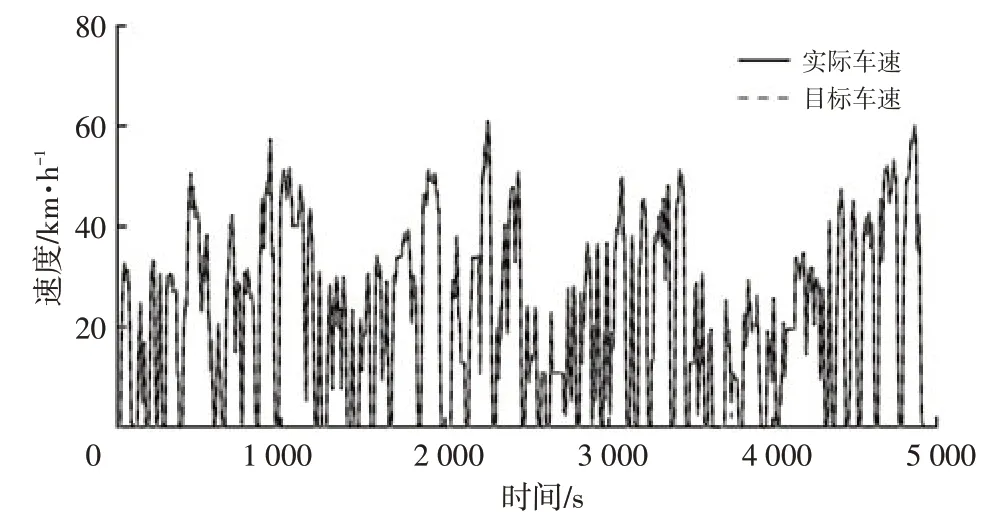
图12 车速跟随情况

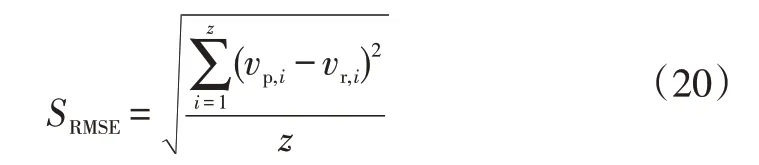
式中，SRMSE为均方根误差；vp,i和vr,i分别为实际车速和目标车速；z为所构建行驶工况时间样本数量。

实际车速和目标车速的均方根误差保持在0.15内，说明优化后的PHEB 动力系统参数能满足实际运行的动力需求。电池SOC较优化前下降平缓，说明电机能在更长时间内发挥辅助作用，实现动力系统的高效工作。

5 结束语

本文提出了一种基于运行数据驱动的混合动力客车动力系统参数优化方法流程，并在此基础上搭建了基于运行数据的PHEB动力系统参数优化模型，构建了具有代表性且符合实际特点的某市城市公交客车行驶工况（RBC），作为动力系统参数优化的目标工况。基于最优拉丁超立方设计的动力系统参数双层优化模型仿真结果表明，该模型优化结果较基于固定整车质量的动力系统参数优化结果和优化前100 km燃油消耗量分别平均减少了7.41%和9.97%，有效发挥了动力系统节能潜力，并验证了所提出模型方法的有效性。

下一步研究重点为，在基于运行数据的客车动力系统参数优化的基础上，利用机器学习、强化学习方法对控制策略进行升级改进，开展自适应优化控制方法研究，利用软件调控实现复杂交通环境下的自适应控制，通过驱动型控制策略对运行数据进行在线识别，提高城市复杂交通环境下城市公交客车的适应性。