基于单值中智集的改进VIKOR法及其应用

叶万红, 耿娟娟*, 徐东胜

(1.四川工业科技学院，电子信息与计算机工程学院, 四川，德阳 618500;2.西南石油大学，理学院, 四川，成都 610500)

0 引言

多属性决策是指在已有的决策信息下对备选方案进行排序或者择优，它在能源、政治、环境和商业等领域有着广泛的应用[1]。但在实际的现实生活中，由于存在很多不确定和不完整的信息，所以很多属性不是用精确的数来表示，而是用不精确的数或者语言来表示和描述。针对这种问题，ZADEH[2]首次提出了模糊集，它可以解决具有不确定信息的决策问题,但模糊集只有一个参数，无法解决较为复杂的决策问题；ATANASSOV[3]对模糊集进行了改进，提出了直觉模糊集和区间模糊集，但是精确度不高;SMARANDACHE等[4]提出了中智集的概念，它是模糊集和直觉模糊集的一种拓展，更具有广泛性，但是考虑到中智集是定义在非标准的子区间，不便于应用在工程和科学上;WANG等[5]提出了单值中智集，它是中智集的子类，利用真隶属度、假隶属度和不确定函数共同描述决策信息，可以方便地应用在工程和科学等领域内。近几年来，中智集与TOPSIS和TODIM法相结合，并应用在很多领域中[6-7]。

OPRICOVIC[8]首次提出了VIKOR的评价方法，由于VIKOR法能够考虑属性之间的相互冲突的特点，因此被很多学者用到多属性决策理论中。OPRICOVIC[9]将拓展的VIKOR评价方法和超序方法二者进行了比较，SANAYEI[10]给出了基于模糊集理论与VIKOR方法的多属性决策模型，并将此模型应用在供应商的选择问题中。ZHANG[11]使用拓展的TOPSIS法和VIKOR方法去处理不确定的多属性决策问题。LIAO[12]提出了一种基于犹豫模糊集环境下的VIKOR法。但是现有关于中智集环境下的VIKOR法的研究还比较少,因此为了解决上述问题，本文提出了一种基于单值中智集环境下的VIKOR评价方法并应用在供应商的选择问题中。首先给出了单值中智集的概念及运算；然后定义了相对距离，为了弥补VIKOR的不足，对它进行了改进；接着在单值中智集环境下，利用改进的VIKOR方法得出各个备选方案的排序；最后通过实例和比较分析说明该方法的有效性和合理性。

1 相关理论知识

1.1 单值中智集

定义1[5]令Y是一个非空集合，y为它的元素，若真隶属度函数uA(y)、不确定函数wA(y)及假隶属度函数vA(y)满足

uA(y):Y→[0,1]；wA(y):Y→[0,1]；vA(y):Y→[0,1],

则称集合A为Y上的单值中智集。

设A为定义在Y上的一个单值中智集，当Y连续时，A可以表示为

(1)

当Y离散时，A可以表示为

(2)

定义2[13]设X1,X2,…,Xn是论域Y上的单值中智数，记Xj=〈uXj,wXj,vXj〉，Xj的权重为ej(j=1,2,…,n)，单值中智集的加权平均算子定义如下：

(3)

1.2 两个单值中智集的距离公式

定义3[14]设A={〈uA(yi),wA(yi),vA(yi)〉}和B={〈uB(yi),wB(yi),vB(yi)〉}为2个单值中智集，A、B之间的标准Hamming距离和标准Euclidean距离分别定义如下：

(4)

(5)

2 基于单值中智改进VIKOR的低碳供应商模型选择

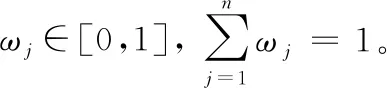
Step1 确定决策专家权重

根据评级的语言术语确定决策专家重要性的单值中智数，设第k位专家对应的单值中智数为Rk=〈uk,wk,vk〉，则决策专家的权重[7]为

(6)

Step2 构建聚合专家权重的单值中智决策矩阵R

利用定义1中式(1)构建聚合专家权重的单值中智决策矩阵R如下:

R=〈uij,wij,vij〉m×n=

(7)

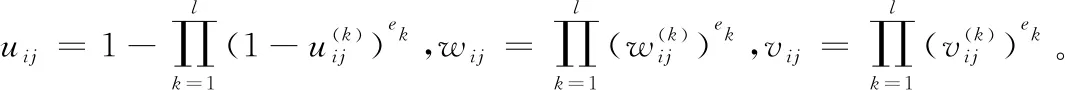
Step3 确定单值中智数正理想解方案X+和负理想方案X-

Step4 利用最小化方案与正理想解距离确定属性的权重

0≤ωj≤1,j=1,2,…,n

(10)

通过构造Lagrange函数对模型(10)的条件约束问题进行求解。设Lagrange乘数为λ，则Lagrange函数为

(11)

式(11)两端分别对ωj和λ求导可得：

(12)

式(12)是关于ωj(j=1,2,…,n)和λ的方程，解出权重值ω1,ω2,…,ωn，并对权重值进行标准化处理。

Step5 计算相对群体效用值ΔSi和相对个体遗憾值ΔRi

(13)

Step6 获取折衷评价值ΔQi

(14)

Step7 对ΔSi、ΔRi及ΔQi分别进行优劣排序，并确定最佳的低碳供应商

按照ΔSi、ΔRi及ΔQi的数值大小对备选的低碳供应商进行降序排列，得到3个排序序列ΔSδ、ΔRσ和ΔQσ。若X(1)是ΔQσ中排名第1的低碳供应商，如果它同时满足下面2个准则，则被视为最佳低碳供应商。

准则1 可接受优势准则

若X(2)是ΔQσ中排名第2的低碳供应商，那么ΔQσ(X(1))-ΔQσ(X(2))≥1/(m-1)。其中，m是低碳供应商的数目。

准则2 可接受稳定准则

若X(1)在序列ΔSσ或ΔRσ中排名也是第1，那么X(1)在决策中是稳定的。

3 实例分析

Step1 确定每位决策专家权重

通过式(6)计算出3位决策专家的权重向量为e={0.406,0.368,0.226}。

Step2 构建聚合专家权重的中智决策矩阵R

利用单值中智加权平均集结算子，将决策专家权重和每个备选方案的单值中智矩阵进行聚合，得到中智决策矩阵R=〈uij,wij,vij〉m×n。

这里仅仅以〈u11,w11,v11〉为代表给出计算过程，通过式(3)，计算可得：

w11=0.100.406·0.200.368·0.500.226=0.186

v11=0.100.406·0.150.368·0.500.226=0.167

同样的，可以计算出矩阵R中剩余的元素，于是得到了聚合专家权重的单值中智决策矩阵。

Step3 确定单值中智数:正理想解方案X+和负理想方案X-

根据式(8)和式(9)，求出正理想解方案X+和负理想方案X-：

Step4 利用最小化方案与正理想解距离确定属性的权重。

利用式(5)计算出方案与正理想方案之间的距离，结果代入式(10)，进而得到如下模型：

maxz=0.24ω1+0.13ω2+0.15ω3+0.19ω4

0≤ω1,ω2,ω3,ω4≤1

对上述模型利用LINGO软件可以得到属性的权重值为ω1=0.657 8，ω2=0.356 3，ω3=0.411 1，ω4=0.520 8。

标准化后的权重为ω1=0.338 0，ω2=0.183 1，ω3=0.211 3，ω4=0.267 6。

Step5 计算相对群体效用值ΔSi和相对个体遗憾值ΔRi

根据式(5)和式(13)，算出ΔSi和ΔRi的值，见表1。

Step6 获取折衷评价值ΔQi

由式(14)计算出4家供应商的折衷评价值ΔQi，在本例中选取λ=0.5，这就意味着采用折中均衡的方法进行方案的选择。计算结果见表1。

Step7 对ΔSi、ΔRi及ΔQi分别进行优劣排序，并确定最佳的低碳供应商

由表1可知，根据折衷评价值得到4家供应商的优先顺序为X4≻X1≻X3≻X2且妥协解为X4。

表1 单值中智集环境下的改进VIKOR方法的结果及排序

下面检验是否满足准则1、准则2：

(1) 由于ΔQσ(X4)-ΔQσ(X1)=0.338 3>1/3，故准则1满足;

(2) 根据ΔSi和ΔRi的值，供应商X4也是最佳妥协解，故准则2满足。

因此，供应商X4为4家备选低碳供应商中的最佳方案。

在使用中存在逆序性问题，而改进的VIKOR法避开了此问题，因此，改进的VIOKR法在实际的应用中有着较强的实用性、合理性和可行性。

4 总结

本文提出了一种基于单值中智数的改进VIKOR法的低碳供应商选择模型，首先，通过语言变量确定了决策专家权重，用最小化方案与正理想解距离确定了属性权重。其次，给出了相对距离的定义，并将其应用在VIKOR法的模型中，改进了VIKOR模型。最后，将改进的VIKOR方法拓展到单值中智集环境下，并通过低碳供应商的选择进行算例分析、灵敏度分析，验证了本文所提决策方法的有效性、稳定性和实用性。