(i,k)-步双极单值中智竞争图
韩晓影,李瑞娟,张新鸿
(1.山西大学 数学科学学院,太原 030006;2.太原科技大学 应用科学学院,太原 030024)
本文中涉及到的有向图是无环、无多重弧的简单有向图。

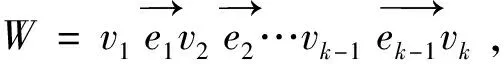
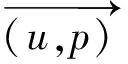

双极模糊集[3]是模糊集[4]的推广,它的隶属度为[-1,1].在双极模糊集中,一个元素的隶属度为0表示该元素与对应性质不相干,元素的隶属度为[0,1]表示该元素满足性质的程度,隶属度为[-1,0]表示该元素满足相反性质的程度。在许多领域中,运用双极信息是很常见的,其中正面信息被认为是可能的,而负面信息被认为是不可能的。例如当评估应聘者是否适合某职位时,正面信息表示应聘者适合该职位的程度,而负面信息表示应聘者不适合该职位的程度。从而引出了双极模糊图[5]。
中智集[6]是模糊集和直觉模糊集[7]的推广,它通过真实隶属函数、不确定隶属函数和失真隶属函数这三个函数定义。由于某些工程和科学问题非常复杂,1998年Smarandache提出了单值中智集[8]的概念。Ye提出了单值中智图[9]的概念。将双极模糊集和中智集结合在一起得到了双极单值中智集[10]。2018年Delietal提出了双极单值中智有向图[11]、双极单值中智竞争图、m-步双极单值中智经济竞争图等概念。由于现实中存在不同步的竞争关系,因此对(i,k)-步双极单值中智竞争图的研究是有必要的。模糊图的应用非常广泛,例如工程学[12],医学,人工智能等。在本文第四部分将举例(i,k)-步双极单值中智竞争图在市场竞争中的应用。
1 准备工作
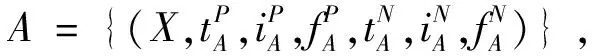


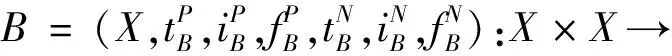
在本文中用x∧y表示min{x,y},用x∨y表示max{x,y}.
定义5双极单值中智有向图为D=(A,B),其中A为顶点集X上的双极单值中智集,B为顶点集X上的双极单值中智关系,且对所有u,v∈X有:



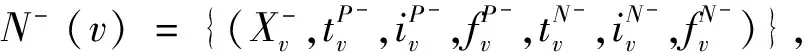
定义9双极单值中智有向图D=(A,B)中的双极单值中智竞争图为(D)=(A,R),其中双极单值中智顶点集与D的双极单值中智顶点集相同,在(D)中有(u,v)边当且仅当N+(u)∩N+(v)是D中一个非空双极单值中智集,(D)中边(u,v)的正真实隶属值、正不确定隶属值、正失真隶属值和负真实隶属值、负不确定隶属值、负失真隶属值分别为:




由m-步双极单值中智经济竞争图的定义,类似可得出m-步双极单值中智竞争图的定义。
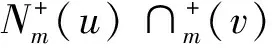
2 (i,k)-步双极单值中智竞争图




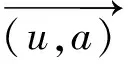
(N+(u)∩N+(v)),
(N+(u)∩N+(v)),
(N+(u)∩N+(v)),
(N+(u)∩N+(v)),
(N+(u)∩N+(v)),
(N+(u)∩N+(v)).

例1设D=(A,B)是双极单值中智有向图,如图1所示。

图1 双极单值中智有向图D
故D的(2,3)-步双极单值中智竞争图2,3(D)如图2所示。

图2 (2,3)-步双极单值中智竞争图2,3(D)
定理1设D=(A,B)是一个双极单值中智有向图,如果
只包含一个元素,则i,k(D)中的(u,v)边是独立强的当且仅当:
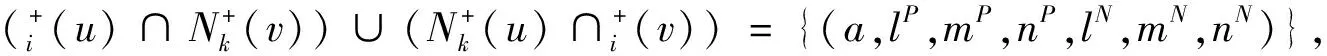
从而:
要使Ci,k(D)中的(u,v)边是独立强的当且仅当lP>0.5,mP>0.5,nP<0.5,lN<0.5,mN<0.5,nN>0.5,即:
定理2设D=(A,B)是一个双极单值中智有向图,如果i>|D|或k>|D|,则D的(i,k)-步双极单值中智竞争图i,k(D)中没有边。

因此Ci,k(D)中没有边。
下面介绍(i,k)-步双极单值中智有向图的竞争图与(i,k)-步双极单值中智竞争图之间的关系。
定理3若D=(A,B)是双极单值中智有向图,Di,k=(A,B′)是D的(i,k)-步双极单值中智有向图,则CC(Di,k)=Ci,k(D).




故在Ci,k(D)中有
从而:
因此证明了CC(Di,k)中的每条边在Ci,k(D)中都存在。同样Ci,k(D)中的每条边在CC(Di,k)中也都存在,因此CC(Di,k)=Ci,k(D).
3 应用

下面给出具体的例子。供销商a,b,c,d,e和它们之间的货运关系的正真实隶属值、正不确定隶属值、正失真隶属值和负真实隶属值、负不确定隶属值、负失真隶属值分别如表1,表2所示。
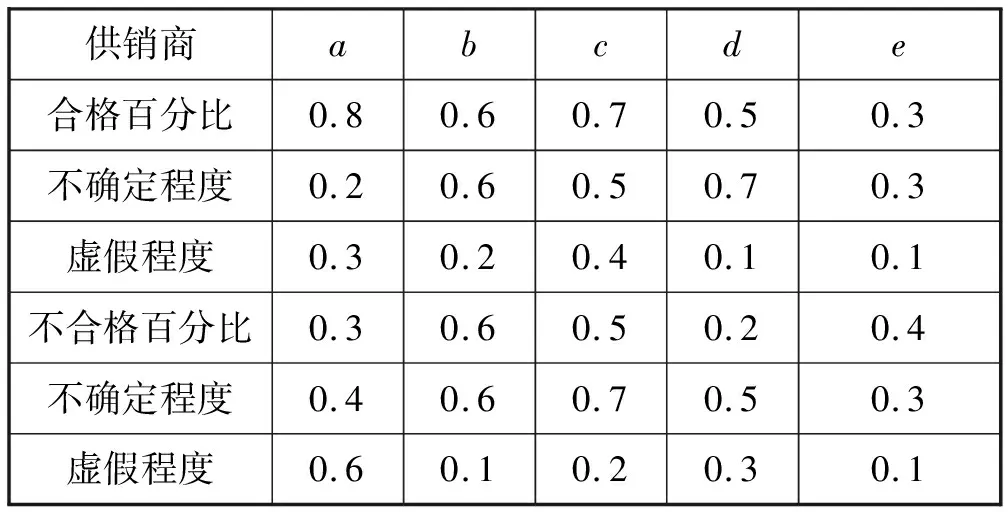
表1 每个供销商的各个隶属值

表2 供销关系的各个隶属值
转化为双极单值中智有向图如图3所示。
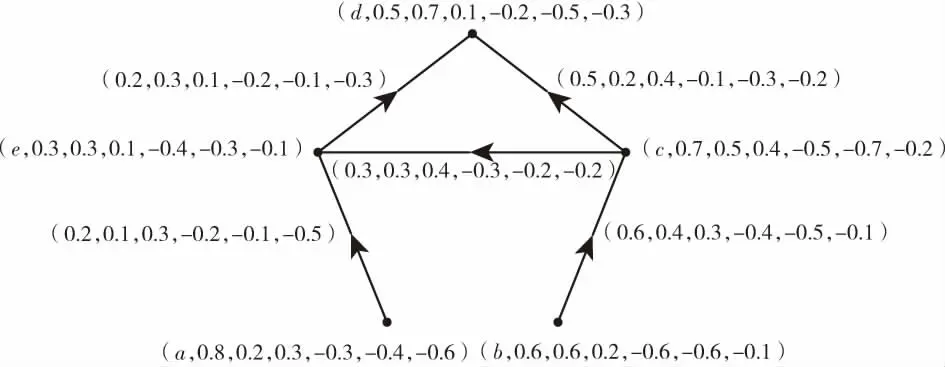
图3 极单值中智有向图D
在D中,每个供销商的2-步外邻集和3-步外邻集如表3所示。

表3 每个供销商的2-步外邻集和3-步外邻集
则:
{(d,0.2,0.1,0.4,-0.2,-0.1,-0.5)},
{(d,0.2,0.3,0.4,-0.2,-0.1,-0.3)}.
因此在D的(2,3)-步双极单值中智竞争图中有(a,b)边和(b,c)边,即供销商a与供销商b、供销商b与供销商c之间存在竞争关系且:

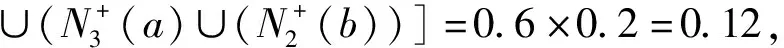

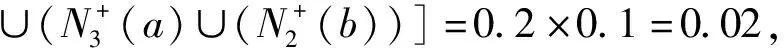
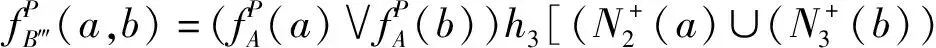


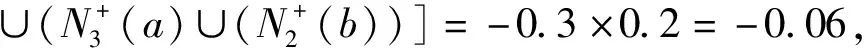
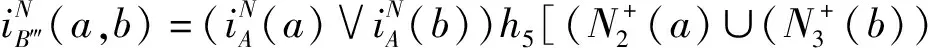
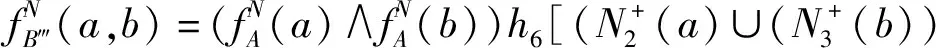

故D的(2,3)-步双极单值中智竞争图如图4所示。

图4 (2,3)-步双极单值中智竞争图2,3(D)
4 总结
本文介绍了(i,k)-步双极单值中智有向图和(i,k)-步双极单值中智竞争图的定义,建立了它们之间的关系,并举例说明(i,k)-步双极单值中智竞争图在市场竞争中的应用。

