无线充电系统电能传输距离的研究
郭 楠,宋卫平,宁爱平
(太原科技大学 电子信息工程学院,太原 030024)
无线充电技术(wireless charging technology)的实现,使得人类摆脱线缆的束缚,电能的使用方式变得更加宽广和灵活,深刻地影响人类的生活。2011年10月,“无线电能传输技术”专题学术沙龙的召开,更推动该项技术朝着成熟化、商业化的方向迈进[1]。与远距离的微波辐射式和短距离的电磁感应式相比,磁耦合谐振式无线电能传输技术(magnetic coupling resonance wireless power transmission,MCR-WPT)作为中距离无线电能传输技术的代表,有着较远的传输距离、较大的传输功率、较高的传输效率等特点,具有更为广阔的发展空间[2],因此受到了较多研究者的广泛关注。
近年来,国内外学者主要从电源器件[3-4]、拓扑结构[5]、线圈设计[6-7]、传输结构[8]、传输特性[9-10]等多方面展开研究。大量学者针对采用串联或者并联电容补偿的双线圈MCR-WPT进行了深入分析,耦合模理论和互感理论广泛用于分析系统的各项传输性能,然而,系统对距离的敏感度仍然是这项技术的一个瓶颈。在传统的双谐振线圈MCR-WPT中,随着距离的增大,两个谐振线圈之间的磁耦合逐渐减弱,导致系统的传输效率降低。本文采用带中继线圈的三线圈结构MCR-WPT来进一步改善这一问题[11]。首先从理论上推导出双线圈和三线圈结构中系统传输效率和传输距离的关系,然后通过编程仿真进行了一系列的分析,最后通过搭建Matlab模型,分别对两个系统的结果进行验证。
1 双线圈MCR-WPT系统传输距离的分析
从能量传输的角度来看,至少需要两个线圈来传输能量,双线圈结构就是使用两个线圈进行电能传输,串-串(SS)结构为其中的一种,也是最基本的一种拓扑结构,为了简便起见,本文以SS双线圈结构作为基础展开分析,其抽象模型如图1所示。从电路理论的角度出发,双线圈的等效电路图可以通过该抽象模型得出,如图2所示。

图1 两线圈模型图

图2 两线圈等效电路图

(1)
式(2)、式(3)分别为LC串联谐振角频率和耦合系数的表达式:
(2)
(3)
根据式(2)和式(3),式(1)进一步表示为:
(4)
通过求解式(4)得到:
(5)

双线圈结构的系统传输效率可以表示为负载消耗的功率与电源的输出功率之比[12],即:
(6)
将式(5)带入式(6),得到双线圈结构系统效率的完整表达式为:
η=
(7)
由式(7)看出,系统的输出效率与线圈自身参数、谐振角频率、系统工作角频率、负载阻值及耦合系数的大小有关。为了直观分析,本文在线圈自身参数及负载阻值确定的情况下,且线圈工作在谐振状态时,研究输出效率与系统工作角频率、耦合系数之间的变化规律。
根据Neumann公式[12]进行推导并结合耦合系数的定义得:
(8)
其中,r1、r2分别表示发射线圈和接收线圈的半径;d表示两线圈间的传输距离。
从公式(8)可以发现,在确定线圈本身的参数后,影响耦合系数的唯一因素是两个线圈之间的传输距离d.通过编程仿真来表达系统输出效率与谐振频率、传输距离三者之间的关系,仿真参数如表1所示,其中,发射线圈回路与接收线圈回路采用相同的参数。

表1 仿真参数
基于表1中的仿真参数,随着谐振频率和两线圈间距离的变化,系统的效率变化如图3所示。

图3 两线圈系统的效率变化图
从图3(a)可以看出,在两个线圈之间的距离逐渐增大的情况下,系统的传输效率呈逐渐降低的趋势,故总体传输效率与传输距离之间存在单调递减的关系。其中,当电源实际工作角频率与线圈谐振角频率相等,即ω=ω0=500 rad/s时,系统的效率要高于其他角频率下的值,并且达到最大效率工作状态,此时的传输效率随距离的变化如图3(b)所示,在距离为0.41 m之前,系统的传输效率较为稳定,且在0.41 m时,效率为93.3%,当距离超过0.41 m后,效率急剧下降。
2 三线圈MCR-WPT系统传输距离的分析
根据图3的分析结果发现,双线圈式MCR-WPT中,其效率对两线圈之间的距离较敏感,当传输效率超过一定的值之后,传输距离就会较小。中继线圈可以作为一个耦合增强器来引入到传统的双线圈MCR-WPT系统模型中,从而达到提高系统传输距离的目的。图4为加入中继线圈后的三线圈结构的抽象模型,其等效电路如图5所示。

图4 三线圈模型图
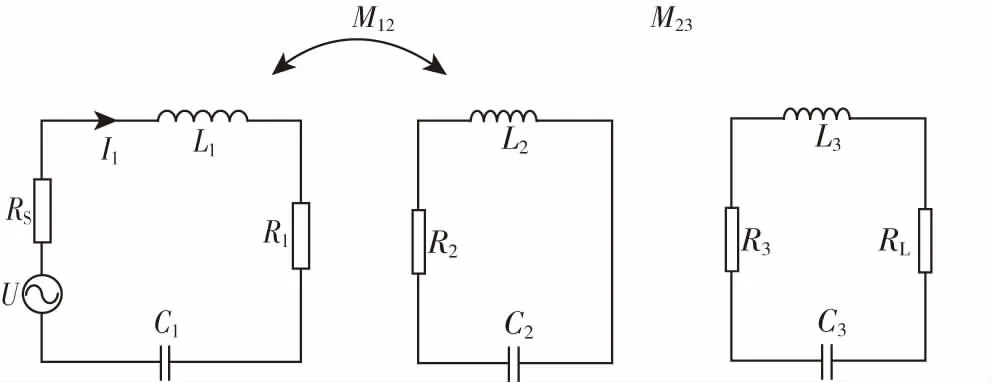
图5 三线圈等效电路图

(9)
通过解公式(9)求得:
(10)

对于该三线圈结构,其系统传输效率表示为:
η=
(11)
由式(11)看出,三线圈结构系统的输出效率除了与谐振频率,还与k12、k23有关,且k12对应发射线圈和中继线圈之间的距离d1,k23与中继线圈和接收线圈之间的距离d2相对应。
3 仿真实验及结果分析
式(11)的效率表达式也从理论上证实,可以通过改变d1和d2的方法,从而改变系统的效率。接下来首先研究传输效率随着d1和d2的变化关系,如图6(a)所示,然后在确定d1的基础上,研究随着总距离d的改变,输出效率的变化情况,其结果如图6(b)所示。且中继线圈回路的参数与上文表1中的参数取值相同,系统角频率工作在线圈谐振角频率。
从图6(a)可以看出随着d1和d2的增大,系统效率整体呈下降的趋势,其中,当d1固定时,随着d2的增大,效率为先增大后减小;当d2不变时,随着d1的增大,效率逐渐下降。为了更直观的表达系统效率随着发射线圈与接收线圈之间总距离的变化情况,图6(b)在确定d1的基础上,分别显示了线圈之间不同距离分别对应的传输效率,可以发现,随着总距离在逐渐增大,传输效率呈现出先增大后减小的趋势,与图6(a)所示的结果一致。当发射线圈与中继线圈之间的距离d1在逐渐增大的过程中,系统传输效率对应的最大值在逐渐降低。当d1为0.2 m,d2为0.41 m时,此时系统可以取得较高的传输效率为93.3%,与上文中的两线圈结构相比可发现,在同等较高效率的情况下,此时系统总的传输距离为0.61 m,比两线圈增大了0.2 m.因此,加入一个中继线圈能够在一定的程度上提高系统传输距离。

图6 三线圈系统效率变化图
根据等效电路图2和图5,在Matlab环境下分别搭建双线圈和三线圈结构的仿真电路模型,如图7所示。将双线圈系统模型中两线圈间的间距取值为0.41 m,在三线圈结构模型中,发射线圈与中继线圈之间的距离d1以及中继线圈与接收线圈间的距离d2分别取0.2 m、0.41 m,模型中其它参数的取值均与上文相同,仿真结果如图8所示。

图7 电路模型图

图8 电流仿真波形
从图8(a)中可明显得出,当系统为双线圈模型并且距离取值为0.41 m时,在发射回路中,电流I1的幅值为0.37 A,接收回路中,电流I2幅值为1.87 A,将数值代入上文的公式(4)、(5)中,进一步计算可求得此时系统的传输效率为93.3%,与图4所示的分析结果取得一致。图8(b)中,当系统为三线圈结构的模型且发射与接收线圈之间的总距离取值为0.61 m时,发射回路中的电流I1幅值为0.92 A,中继回路的电流I2幅值为0.57 A,接收回路的电流I3幅值为2.9 A,同理代入上文式(9)、(10)中,通过进一步计算得出系统的传输效率为93.3%,验证结果与图7所示结果相吻合。由此可以看出,在双线圈结构中加入一个无载、无源的中继回路,可以在系统传输效率较高且稳定的同时,有效地提高系统的传输距离。
4 结论
本文首先对传统双线圈结构MCR-WPT系统进行了理论分析,为了解决该系统传输距离较短这一问题,采用了带单中继线圈的三线圈结构,并对该结构展开研究,根据系统数学模型,从理论的公式推导和编程仿真方面进行一系列分析,并通过在Matlab环境中搭建模型验证,最后结果表明:当线圈的谐振频率与系统工作频率相等时,此时传输效率高于其他频率下的值,并且达到最大效率工作状态。双谐振线圈MCR-WPT系统传输距离在0.41 m之前时,传输效率较为稳定,且能达到93.3%以上,但当传输距离大于0.41 m后,传输效率则会急剧下降。在带有中继线圈的三负载MCR-WPT系统中,最大传输效率点则会随着d1的增大而逐渐降低,当d1为0.2 m,d2为0.41 m时,相比两线圈结构,在同等效率的情况下,系统的总传输距离增大了0.2 m.

