基于最小跳数改进的三维DV-Hop定位算法

胡 远，乔建华

(太原科技大学电子信息工程学院，太原 030024)

无线传感器网络(WSN)是指将大量的具有通信与计算能力的微小传感器节点，通过人工布设、空投、火炮投射等方法布置在预定的监控区域[1]，构成的智能自治监控网络系统，可以将感知和计算后的相关信息传输到计算机终端，实现对监测区域的信息采集和监控[2]。较早的定位技术只是局限于在二维平面区域内研究的，随着科学技术的发展和进步，二维定位算法已经不能满足许多定位需求，无线传感器网络定位技术也逐渐发展到三维空间网络中[3]。例如越来越多的建筑物的外形采用壳体，由于其特殊的外形给检查和维修带来了较大的麻烦，利用三维节点定位技术和传感器技术就可以对故障进行初步定位，给建筑物维修带来很大的便利。通过在地形不平整的山区地形布设无线传感器网络，从而可以运用三维定位技术来监控预防泥石流、山体滑坡等大型地质灾害的发生[4]。

近年来随着传感器网络定位技术的发展应用许多定位算法被提出，这些定位算法主要分为两类：基于距离的定位算法和无需距离的定位算法，前者主要利用到达时间(TOA)[5]、到达时间差(TDOA)、接收信号强度(RSSI)[6]等方法，距离信息容易受到多径衰落和环境的影响，另一方面功耗较高使得该算法无法大量使用。无需距离的定位算法主要有质心算法[7]、DV-Hop算法以及APIT 算法等，这些算法功耗小且可以满足大部分应用的定位需求，因此得到更多研究。董静薇等人针对DV-Hop算法的缺点，将基于距离和无需距离两种定位方法相结合，引入了RSSI测距技术对平均每跳距离计算进行修正，提高了定位精度[8]；刘桂琦等人使用改进的微分进化算法对DV-Hop进行改进，减小了定位误差[9]；任克强等人提出将二维双曲线法应用到三维空间定位，结果比原始算法定位精确[10]；刘志贵等人基于APIT算法提出一种APIT-3D算法并进行改进，使得定位算法应用更加广泛[11]；Xiao Chen等人在三维定位基础上提出粒子群优化技术的方法，较好的使用了群体智能算法的优点[12]。沈世凯等人提出了基于概率信息的锚节点选择方法，并采用二维双曲线函数来预测未知节点的位置，实验表明算法定位精度较高[13]。崔志华等人提出一种新的杜鹃搜索算法对DV-Hop算法定位性能进行优化改进，仿真结果表明改进后的算法具有更好的精度[14]。

本文在分析和学习二维DV-Hop基础上，进一步将此算法扩展到了三维无线传感器网络的定位中，并在此基础上提出了基于双通信半径的改进算法。以基于CC2530的无线传感器网络为例，无障碍无功放传输距离为(10～200)m，可以通过改变TXPOWER寄存器的值来改变发射功率大小得到两个通信半径，使得节点间的最小跳数更加接近真实值[15]，明显提高了三维DV-Hop定位精度。

1 三维DV-Hop定位算法

1.1 算法描述

三维DV-Hop定位算法主要通过节点的三维坐标计算来对立体空间中的一些目标进行定位研究[16]。

(1)获得所有节点之间的最小跳数值

开始定位时，锚节点i向网络中广播数据包，这些数据包主要包含锚节点i的标号、跳数值以及位置等信息，并将跳数初始值设置为0，接收到数据包的 节点首先检查自己是否接收过来自这个锚节点发出的信息。如果此前没有接收过该数据包，就把数据包中的跳数值保留下来，然后把该跳数值加一继续转发到网络中去；如果接收过，则进行跳数比较并仅保存跳数较小的跳数值再将跳数加一继续转发，直到所有节点都计算出到每个锚节点的最小跳数。

(2)计算未知节点的平均每跳距离

通过第一阶段网络中锚节点数据包洪泛后，每个锚节点都记录了与其它锚节点的所有跳数值和三维坐标，可以用公式(1)估算出每一跳的距离。

Hopsizei=

(1)

上式中表示锚节点i的平均每跳距离，式子中(xi,yi,zi)表示Hopsizei锚节点i的三维坐标，(xj,yj,zj)表示锚节点j的三维坐标，hij表示求出的锚节点i和j间的最小跳数。

(3)计算未知节点的坐标

计算出每一跳的距离后，每一个锚节点通过网络洪泛平均每跳距离，未知节点在计算与锚节点的距离时使用收到的第一个平均每跳距离，当未知节点得到4 个或4 个以上锚节点的距离后，可以选择用四边测量法或极大似然估计法来确定自己的位置坐标。

假设待定位节点U坐标为(x,y,z)，锚节点坐标为(xi,yi,zi)，两者之间所求距离用di表示，得到(2)式。

(2)

节点U的坐标可由下式求出：

X=(ATA)-1ATB

(3)

其中

A=

B=

1.2 三维DV-Hop定位算法示例

在图1中，U表示未知节点，L1,L2,L3,L4表示四个锚节点，根据前面的定位算法可以求出L2的平均每跳距离Hopsize2.

图1 DV-Hop算法示意图

Hopsize2=(40+60+20)/(2+5+1)=15 m

从拓扑图中可以看到未知节点到锚节点L1,L3,L4的最小跳数都为三跳，距离L2的最小跳数为两跳，根据1.1介绍的定位算法，可以求出节点U到周围四个锚节点的距离公式如下：

然后再应用极大似然估计法就可以估算出未知节点的位置。

2 三维DV-Hop算法存在的问题

在原始三维DV-Hop 定位算法中，网络中的所有节点都是随机抛撒的，节点的位置分布不均衡，尤其在三维空间定位分布更广泛，不同节点间的拓扑结构图大部分都不是直线路径，而是通过其他节点连接起来的，在计算节点间的距离时如果用直线路径求得的距离进行计算，就会与实际距离有较大的偏差，会对最终的定位效果产生消极影响。

原始三维算法在计算节点间距离时，使用收到的第一个锚节点的平均每跳距离与跳数相乘，但是在传感器网络中一个未知节点周围通常有多个锚节点，这样只考虑最近的锚节点而忽略其它锚节点对定位精度的影响，也会影响定位精度的准确性。

3 基于双通信半径的改进三维DV-Hop定位算法

3.1 双通信半径算法

DV-Hop算法定位时，只要在锚节点通信半径R广播范围内的所有节点的跳数都记为一跳，那么在求锚节点的校正距离时就会产生误差，从图2中看到，当区域中间锚节点数据在网络中传播时，四个未知节点都在其一跳的通信半径范围内，所以它们收到的跳数都会增加一，再进行转发，从图中很明显看出它们到锚节点的跳数是有较大差别的，这样用最小跳数乘以校正距离所得的节点间的距离与实际距离会有较大的误差，会对算法定位精确度造成较大影响。以双通信半径进行改进后，图2中节点1到锚节点的跳数就为0.5，节点2,3,4的跳数为1，计算出的跳数更加符合网络拓扑结构，从而定位精度提高。

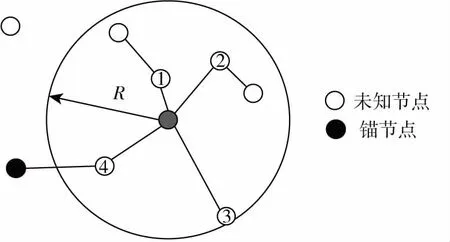
图2 节点一跳区域示意图

3.2 改进算法示例

在图1中，可以求出网络中未知节点U到L1,L2,L3,L4四个未知节点的最小跳数分别为3，2，3，3，在本文经过双通信半径广播以后，可以得到四个节点的最小跳数变为2.5，2，2.5，3，这样求出来的跳数比原始算法里的跳数更加接近真实值，经过计算可以得到未知节点到四个锚节点的距离公式如下：

从上面的计算结果可以看出,求出来的四个距离能较好反映网路中节点的真实拓扑结构，从而使定位结果更加精确。

3.3 改进算法的具体步骤

(1)计算节点间的最小跳数

定位开始时，节点的初始跳数为0，让锚节点以0.5R为通信半径广播自身位置信息，接收到信息的邻居节点将跳数值加上0.5；一段时间后，锚节点再以R为通信半径进行广播，当邻居节点接收到该信息后先判断是否接收过来自该节点的数据信息，如果没有则更新跳数，否则不更新跳数。邻居节点接收到信息以后继续以上过程转发数据。最后网络中所有节点都会记录到每个锚节点的最小跳数信息。

(2)计算未知节点与锚节点之间的距离

当通过第一步广播得到了锚节点与其他节点间的最小跳数以后，所有锚节点由公式(1)计算得到各个锚节点的校正距离，它们之间距离由跳数值与未知节点收到的第一个锚节点的平均每跳距离相乘求得，本文的改进算法可以使求得的距离更加精确，如图2中，未知节点1的跳数记为0.5，就比原始算法中的跳数为1更加接近真实值。

(3)根据以上求出的距离使用极大似然法计算节点位置。

3.4 改进算法的流程图

4 仿真实验与结果分析

本文使用MatlabR2014a软件对算法进行仿真。模拟在长、宽、高都为100 m的立体空间区域内，通过随机抛撒节点的方式自组织形成无线传感器网路，节点总数记为100个，实验通过给锚节点个数和通信半径设置不同数值来比较两种定位算法误差大小，由于无线传感器网络节点分布具有随机性，本文仿真是在经过150次实验求得的平均值，图3是在一次实验中三维空间网络中所有节点的分布情况。

图3 节点随机分布图

采用相对定位误差对两种算法定位性能做对比，公式如下:

(4)

相对定位误差的值越小，说明算法的定位精度越高，上式中(xi，yi，zi)表示估算出的未知节点坐标，(xo，yo，zo)是未知节点真实坐标。

图4设置网络中节点总数为100个，锚节点比例为20%，通信半径为50 m，两种点位算法的定位误差对比情况。从下面图中可以看到，除了极少数的几个节点以外，其他未知节点在改进算法的定位误差明显小于原始三维定位算法，且本文算法的定位误差更加稳定。

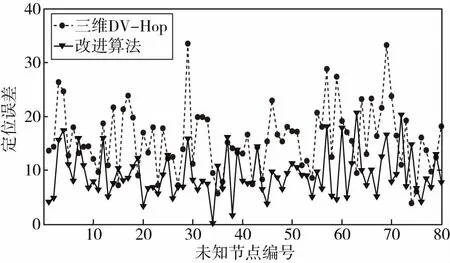
图4 两种算法未知节点误差对比图

图5设置网络中节点总数为100个，通信半径为50 m时，让锚节点个数从10个以5为步长增加到50个，通过仿真得到的误差对比图。从仿真结果看出，当网络中锚节点个数增加时，两种算法的定位误差逐渐变小，且改进算法定位误差远小于原始算法定位误差。

图5 不同锚节点比例定位误差对比图

图6是设置节点总数为100个，锚节点数为20个，通信半径从45 m增加到70 m时两种算法定位误差情况。当通信半径从45 m增大到70 m时，可以看到两种算法的定位误差都在变小。在任意通信半径下，改进的算法都在原有算法的基础上有了很明显的提高。这是因为随着通信半径的增大，未知节点获得的锚节点信息越多，从而锚节点计算出的平均每跳距离比较接近真实值，所以误差会变小。

图6 不同通信半径定位误差对比图

5 结论

本文经过研究原始三维定位算法及已有的改进算法，引入双通信半径来改变节点间最小跳数，使得节点间的跳数更加精确，能较好反映节点分布情况。通过仿真图像可以得到，随着锚节点个数和通信半径的增加，两种算法的定位误差都在减小，并且本文改进的算法比原始三维算法定位误差减小了10%左右。