一种改进的书写机器人曲线路径拟合方法
卢 冉,何秋生,王 垚
(太原科技大学 电子信息工程学院,太原 030024)
在机器人笛卡尔空间规划中[1],机器人末端的运动轨迹一般都是圆弧或者直线,对于一些形状复杂的曲线、曲面,传统的方法是将曲线划分为大量微小直线段或圆弧段,然后进行线性插补。在通过这些微线段的过程中机器人需频繁加减速,可能导致电机振动,降低机器人寿命;对大量微线段的运算处理也会增加系统的负担,影响实时性。针对这些缺陷,一些高档数控系统引入了样条插补功能。
不同于传统的小线段插补或圆弧段插补,样条插补无需将曲线离散化为大量微线段,可直接对参数曲线进行插补,不仅能减少工件的程序量,还能避免机器人的频繁加减速控制,为高速、高精、高质量加工提供了新思路[2-3]。
常用的样条曲线有三次样条曲线、B样条曲线和NURBS曲线等[4-5]。NURBS插补算法的研究一直是数控插补算法研究中的热点和重点[6-7]。目前已经有许多学者针对NURBS的拟合开展了大量研究工作。Yeh和Su等[8]采用了最小二乘法将离散的数据点拟合成连续的NUBRS曲线,然后进行样条插补。Wang和Yau[9]则采用三角形测试和双弦高误差测试识别出连续的加工区域,然后拟合成NURBS曲线进行插补。由于NURBS曲线并不能穿过每一个数据点,其拟合形状有时会与数据点的真实轮廓有一定差距,一些研究人员对此进行了改进。董甲甲[10]在三次均匀B样条曲线基础上进行改进,通过增加控制顶点,获得了一种新的通过型值点、首尾点的B样条曲线,获得了更高精度,且保留了传统B样条曲线局部性、凸包性。陈爽[11]通过曲线反算的方法生成了一条经过所有示教点的曲线,实验证明该方法能以较少的示教点生成所需的复杂曲线,提高了示教效率。孔庆博[12]提出了一种改进的5次多项式插值法,在5次多项式插值的基础上加入B样条插值,优化后的关节曲线更加光滑平稳,能较好地消除突变现象,避免了机器人在运动过程中的振动和冲击。
为了达到平滑路径,提高拟合精度的目的,本文分别分析了三次样条曲线和NURBS样条曲线的优缺点,以实验室六自由度机器人为研究对象,采用改进的曲线拟合方法规划机器人的末端路径,并进行曲线拟合实验,验证方法的有效性。
1 两种样条曲线插值算法
1.1 三次样条曲线
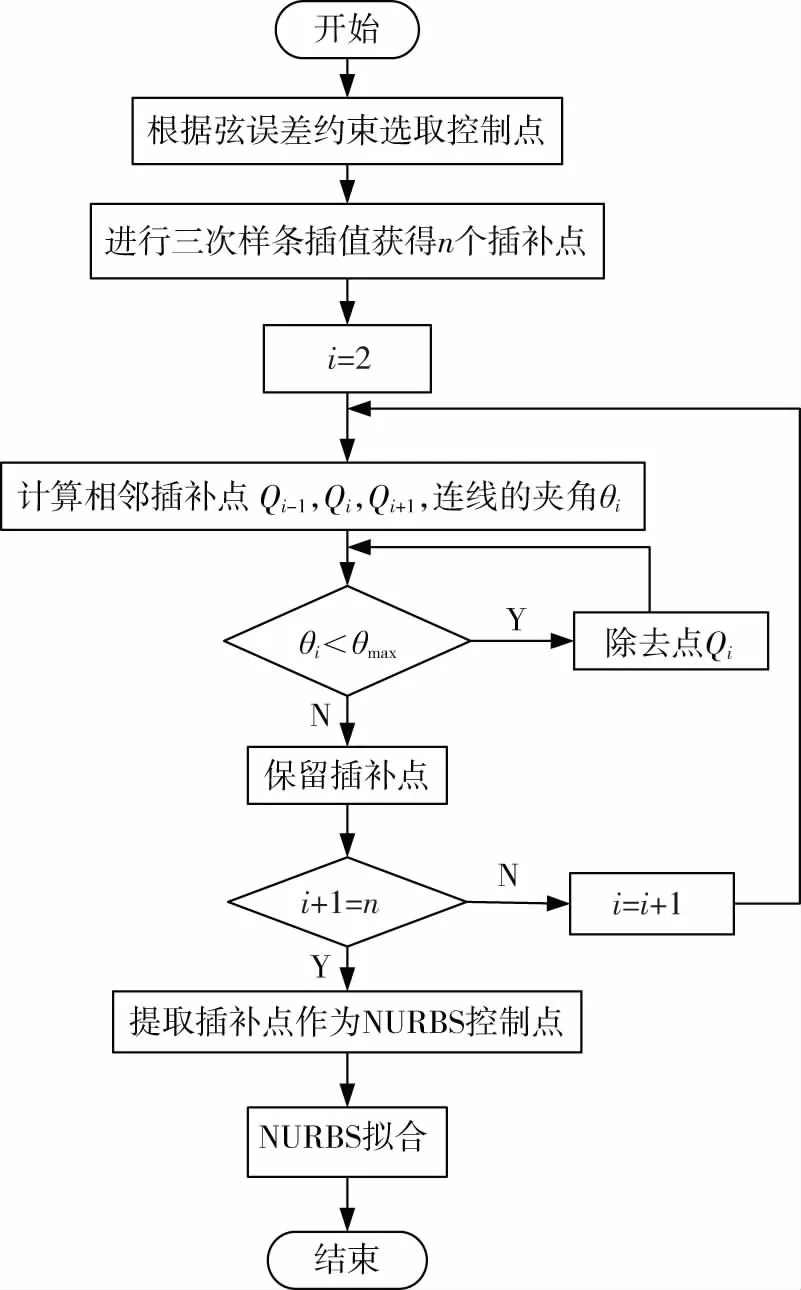
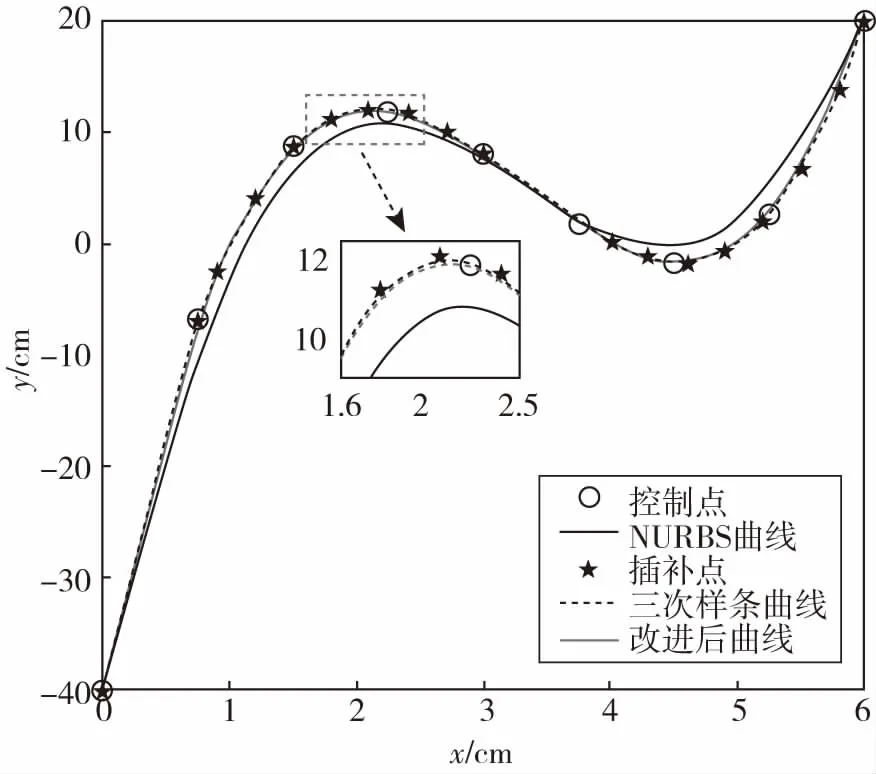
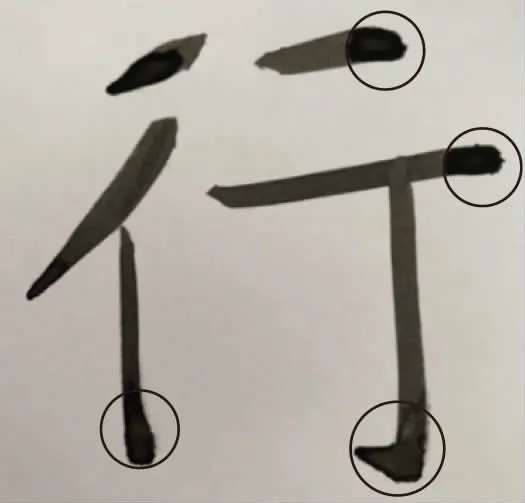
设区间在[a,b]内,通过一组插值节点将其分为小空间,a=x0 (1)在每一个结点上满足S(xi)=yi,(i=1,2,3,…,n-1); (2)在每一个子区间[xk-1,xk](k=1,2,…,n)上,S(xi)是一个不超过三次的多项式; (3)S(x),S′(x),S″(x)在[a,b]上连续。 则称S(x)为结点x上插值与y的三次样条插值函数。 三次样条曲线可以精确的穿过每一个数据点,但是三次样条曲线的局部性较差,任何一个数据点或坐标点位置的改变,会对整个样条曲线产生影响。而且随着路径点的增多,计算的复杂度也随之增大。 NURBS曲线是在贝塞尔曲线和普通B样条曲线的基础上发展来的,且很好的兼容了两种参数曲线。其原理是通过控制点组成的多边形来拟合曲线,能够通过控制顶点及权因子修改曲面与曲线的形状。NURBS曲线的方程可以表示成如下形式[14]。 (1) 其中,u为NURBS曲线的参数,di为控制点,ωi为对应控制点的权因子,Ni,k(u)为定义在非周期节点矢量U=[u0,u1,…,un+k+1]上的k次B样条基函数,基函数的递推公式为: (2) 若{ωi}={1,…,1},则NURBS曲线表达式变为B样条。 NURBS曲线的形状控制功能强大灵活,能统一精确地表示自由曲线和曲面,在曲线局部调整方面优于三次样条插值,但NURBS曲线并不会完整地经过每一个示教点,而对于高精度机器人运动控制系统中,常常需要能经过示教点的样条插值曲线。 对拟合后的曲线参数化,进行NURBS插值时,利用用弦长ΔLi逼近弧长ΔSi的方法。设当前插补点C(ui)理想进给速度为V(u,),理想的下一个插补点C(ui+1)的插补参数为ui+1.根据微分几何,沿曲线移动所需的速度为: (3) 通过上式,可以得到: (4) 本文采用一阶泰勒展开方法来进行参数求解。设T为插补周期,则可得: (5) 通过上式即可算出的参数ui+1对应的插补点C(ui+1)的位置。 为了确保拟合精度同时计算减小量,本文在选取控制点时引入了弦误差约束对方法进行改进。针对三次样条插值与NURBS插值的优缺点,本文采用了对三次样条形成的插补点进行筛选,筛选后的点作为NURBS的控制点的改进的拟合方法。 在进行曲线拟合前,需要选取控制点,为了保证拟合的精度,需要获得关键控制点。但如果控制点太多,小于最大弦误差,就会增加计算量。所以引入最大弦误差来除去多余控制点[13]。 图1所示为弦误差示意图,设Pi-1,Pi,Pi+1是三个相邻的控制点,li-1,li是连接这三个点的直线段。Pi-1,Pi,Pi+1三点可构成一个圆弧,设该圆的半径为R,通过图中几何关系,可得到弦误差σ1,σ2的计算公式为: 图1 弦误差示意图 δ1=R(1-cosβ) (6) δ2=R(1-cos(π-θi-β)) (7) 规定最大弦误差为σmax,如果弦误差σ1,σ2同时小于σmax,则控制点Pi为多余点,移除该点,继续计算下一组相邻控制点的弦误差,直到筛选完所有的控制点,则完成控制点的选取。 如图所示,相邻插补点Qi-1,Qi,Qi+1的连线形成夹角θi,θi的求解公式为: (8) 设定插补点连线间的最大允许夹角为σmax,如果θi<θmax,则移除插补点Qi,继续计算下一组相邻插补点连线的夹角,直到完成所有插补点的筛选,就可以作为NURBS曲线的控制点,其原理与控制点的选取相同。通过夹角约束筛选的插补点作为NURBS曲线的控制点,在达到精度的同时也可以减少计算量。 本文方法的整体流程如图2所示。方法的具体步骤为: 图2 插补点连线夹角示意图 (1)通过引入最大弦误差δmax从离散点中选取合适的控制点; (3)筛选的插补点作为NURBS函数的控制点,根据公式(1)生成NURBS样条曲线。 图3 总体方法流程图 (1)实验一: 在空间中任取九个控制点(0,-40)、(0.75,-6.9)、(1.5,8.75)、(2.25,12)、(3,8)、(3.75,1.71)、(4.5,-1.75)、(5.25,2.65)、(6,20),分别使用传统的NURBS、三次样条和改进的方法进行拟合。如图4所示,图中空心点为控制点,星型点为选取的插补点。 仿真结果如图4所示,通过NURBS拟合的曲线虽然光滑,但没有通过所有的控制点,拟合精度较低。通过插补点连线的夹角选取插补点后,生成的三次样条曲线虽然通过了每个控制点,但平滑性较差。而改进后的拟合曲线整体光滑,相对于三次样条插值减少了计算量,并且通过了每个控制点,提高了曲线拟合精度。 图4 拟合曲线仿真图 为了更清晰的表明本文拟合方法精度的提高,对拟合曲线与期望曲线的误差进行比较。图5和图6分别为传统NURBS曲线和改进曲线的拟合误差,结果表明改进后的方法减小了拟合误差,大大提高了曲线的拟合精度。 图5 NURBS曲线误差 图6 改进后曲线误差 (2)实验二: 根据弦误差提取图7中心形图形的21个控制点,分别使用NURBS、三次样条和改进的方法进行拟合。仿真结果如图8所示,NURBS拟合曲线与与原图形轮廓贴合程度相差较大,根据筛选的插补点拟合的三次样条曲线平滑性较差,本文方法拟合的曲线平滑且与原图轮廓更加贴合,拟合精度较高。 图7 心形图形 图8 心形拟合仿真图 为了更好的验证本方法的可行性和有效性,本文使用实验室现有Denso VP6242G机器人进行毛笔书写实验,图9为机器人实验平台。首先,根据机器人的工作空间选取合适的书写坐标范围,对字体进行轨迹规划,规划时考虑毛笔书法回笔等书写动作的需要,选取字体的关键离散点。然后对离散点进行插值拟合,生成平面的书写轨迹。 图9 机器人实验平台 图10为字体轨迹的仿真结果。考虑到书写动作的落笔、提笔与按笔,对z轴方向还需进行轨迹的设计与规划。把插值生成的插补点数据输入到机器人的simulink位姿矩阵模块。然后控制机器人做出相应的位姿移动进行书写实验。 图11为机器人实际的书写效果,图中圆圈所标记的书写弧度与图10中规划的圆弧轨迹相对应,如图所示达到了预计的弧度效果。结果表明,本文研究的方法能体现处毛笔书写行为中力度大小的变化,在绘制过程中能够较好的实现各种直线、曲线等书法轮廓的控制,字迹光滑,有良好的临摹效果。 图10 水平轨迹仿真 图11 机器人实际书写效果 本文主要对机器人末端路径规划中,使用传统曲线拟合方法拟合精度低、曲线局部性较差的问题,提出了改进的样条拟合的方法,即三次样条插值与非均匀有理B样条相结合的方法。通过Matlab仿真以及机器人书写实验验证,此方法可使机器人生成光滑的运动轨迹,还可以提高曲线拟合精度,使曲线通过每个控制点。1.2 NURBS曲线
1.3 样条曲线插补

2 曲线拟合方法的改进
2.1 控制点的选取

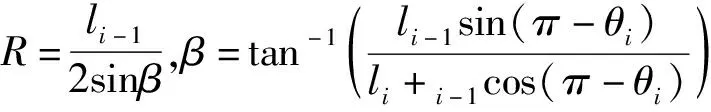
2.2 插补点筛选
2.3 方法整体思路


3 仿真实验与分析
3.1 曲线拟合仿真




3.2 机器人书写实验验证


4 结论

