等弦分割采样的球面插补算法研究

陈 玺，李传军

（1.天津科技大学机械工程学院，天津 300202；2.天津中德应用技术大学机械工程学院，天津 300350）

1 引言

机器人在运动过程中需要沿着特定轨迹运动，如直线、圆弧、球形等。现阶段球面插补算法大都是通过多段圆弧插补实现的，针对机器人的空间圆弧插补主要有矢量法［1-8］、坐标转换法［9-15］、等弧分割法［16］、积分法［17-18］等。所求的插补点需要用到坐标变换，积分运算，微分运算等，增加了运算量。因此对于球面插补算法需要一种计算简单，运算速度快，插补点精确的圆弧插补算法。

本论文提出一种基于等弦采样的新型空间圆弧插补算法，与其他算法相比运算时间大幅减小。通过仿真和样机实验，验证了插补算法的正确性。把这种新型空间圆弧算法应用到球球面插补中，求得空间球面的插补点并求出末端的位姿。通过MATLAB对机器人建模并仿真出球形灌木修剪过程，验证了该算法的有效、可行性。实现了不同尺寸球形灌木自动修剪的仿真。

2 空间圆弧插补算法

提出一种基于等弦采样的新型空间圆弧插补算法。给定空间任意不共线的三个点，即可求出圆心坐标P0与圆弧半径R。由于空间圆弧与弦长有映射关系。

给定圆心坐标，起始点和终止点坐标，插补圆弧的圆心角θ，即可求出插补点。此算法分为两种情况。圆弧的圆心角0 ＜θ＜π和π ＜θ＜2π。

（1）当圆弧圆心角为0 ＜θ＜π时

设给定某圆弧起始点为：Ps=(xs，ys，zs)，终止点为：Pe=(xe，ye，ze)，圆心坐标为：P0=(x0，y0，z0)，圆弧半径为R。则弦PsPe长度L为：

现根据圆弧起始点Ps、终止点Pe求插补点Pi的空间坐标，首先对弦PsPe等分，等分精度为ΔL，如图1（a）所示。

图1 空间圆弧插补原理Fig.1 Principle of Space Circular Interpolation

设圆弧上第i个插补点为Pi，则直线P0Pi与弦PsPe的交点为。Ps长度为：

（2）当圆弧圆心角为π ＜θ＜2π时

设给定某圆弧起始点为：Ps=(xs，ys，zs)，终止点为：Pe=(xe，ye，ze)，圆心坐标为：P0=(x0，y0，z0)，圆弧半径为R。可求得空间圆弧PeP0延长线上的点，空间圆弧PsP0延长线上的点如图1（b）所示：可以求得Pe与Ps直径对点坐标坐标。圆弧的圆心角均属于0 ＜θ＜π，每一段可根据圆心角0 ＜θ＜π时进行插补。

3 圆弧插补算法验证及计算效率分析对比

3.1 圆弧插补算法Matlab仿真验证

（1）当圆弧圆心角为0 ＜θ＜π的情况

设圆弧的起始点：Ps=(81.55，174.76，87.38)终止点：Pe=(42.81，162.68，66.75)，圆心：P0=(70，150，75)。设弦分割精度ΔL=0.1mm绘制圆弧轨迹，如图2（a）所示。

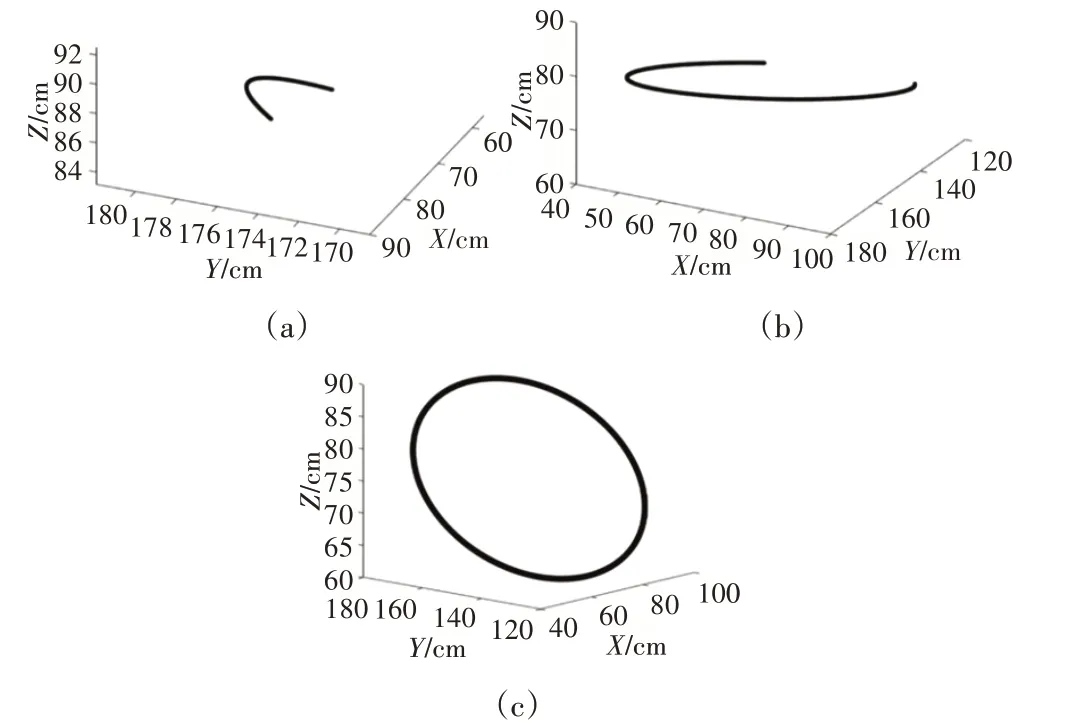
图2 圆弧插补轨迹Fig.2 Arc Interpolation Trajectory

（2）当圆弧圆心角为π ＜θ＜2π时情况

这指的是中国共产党在革命与建设过程中形成的思想、制度、文化等，如在革命战争年代与马克思主义相结合，并与时俱进形成的毛泽东思想、邓小平理论、三个代表、科学发展观、社会主义核心价值观等思想体系以及由此建立的中国特色社会主义制度。

设圆弧的起始点：Ps=(81.55，174.76，87.38)终止点：Pe=(97.18，137.31，34，75)，圆心：P0=(70，150，75)。则直线ps p0与圆弧的交点为=(42.81，162.68，66.75)，直线pe p0与圆弧的交点为P'e=(58.44，125.23，62.61)，设弦分割精度ΔL=0.1mm。绘制圆弧轨迹，如图2（b）所示。

（3）对于θ=2π的整圆情况

3.2 计算效率分析对比

为了验证提出的空间圆弧插补算法的计算效率，在Matlab中本算法与其他常见的算法文献［2、13、16］相比较。以图2（a）为例，在相同圆弧，插补点个数均为1000时，所用运算时间，如表1所示。测试操作系统为64 位Windows10，CPU 型号Intel（R）Core（TM）i7-7700@3.60GHz，32G内存。由表1可知，使用等弦分割采样圆弧插补算法计算插补点在计算时间上明显低于其他算法。

表1 几种常见的空间圆弧插补算法比较Tab.1 Comparison of Several Common Spatial Arc Interpolation Algorithms

3.3 插补算法样机验证

试验样机为五轴混联机器人，前两个自由度为SPU+U并联机构，后三个自由度为串联机构。控制器内嵌TwinCAT 3.1控制软件，可以将任何PC系统转换为PLC、NC模块的实时控制系统，其PLC内置运动控制库“Tc2_MC2”，使用PTP的方式通过外部位置发生器写入数值。实验采用记号笔在白纸上画出圆弧轨迹的方法对上述圆弧插补算法进行验证。机器人所画的圆弧轨迹，如图3所示。坐标单位为厘米，其中图3（a）为圆心角为0 ＜θ＜π，起始点、终止点、圆心坐标分别为PS=(-10，-150.1，135.3)、Pe=(0，-150.1，145.3)、P0=(0，-150.1，135.3)。图3（b）为圆心角π ＜θ＜2π，起始点、终止点、圆心坐标分别为Ps=(0，-150.1，145.3)、PS=(3.42，-150.1，125.9)、P0=(0，-150.1，135.3)。图3（c）为整圆，圆心坐标与半径为，P0=(0，-150.1，135.3)，R=30cm。

图3 样机验证Fig.3 Experiment Validation

图3机器人画出的圆弧轨迹验证了提出算法的可行性，正确性。

4 球面插补算法

机器人在工作的时候，末端需要沿特定的空间球面进行插补。空间球面插补可以看作机器人末端在空间上走了m段径向的半圆。与圆弧插补相比，球面插补所要求的插补点计算更复杂，提出的空间圆弧算法具有计算量小，插补点准确等特点。将提出的圆弧插补算法应用到机器人球面插补之中，求得球面插补点坐标。球面插补算法步骤如下：

（1）设给定空间球心坐标P0与球心半径R，如图4所示。平面M与基座标系z轴垂直并包含球心P0。可求得球面插补辅助点坐标P1-P6。

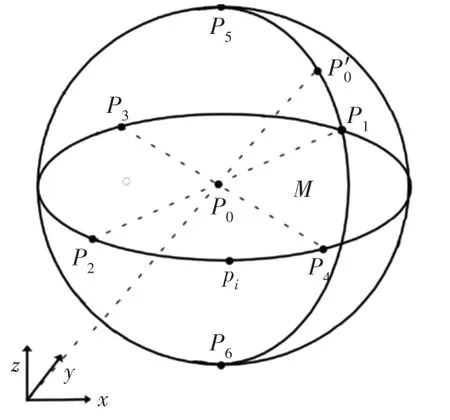
图4 球面插补点坐标示意图Fig.4 Spherical Interpolation Points

设ϕ=atan 2(y0，x0)。则P1-P6的坐标为：

（2）球面可以做m段径向半圆，使用等弦分割采样空间圆弧算法求得P1-P4所在球面大圆m+1个插补点坐标，用于计算机器人插补过程中每段径向半圆姿态。设第j个插补点为Pj=(xj，yj，zj)。则：

式中：ϕj—机器人末端单位向量在基座标上的投影夹角。

机器人末端姿态为：

（3）设每段径向半圆起始点与终止点为Pstart，Pend。Pstart=P5，Pend=P6。Pj为P1-P4所在球面大圆第j个插补点。令j=0。

①使用本算法计算圆弧PstarPj与圆弧PjPend组成的径向半圆中n+1个插补点坐标。

②求解机器人在圆弧PstarPj与圆弧PjPend插补过程中姿态。

③当机器人位于Pend并且j≠m+1时，交换Pstart，Pend。j=j+1时返回至第一步求解下一段径向半圆位姿。当机器人位于Pend并且j=m+1时，结束插补运动。

5 球面插补算法仿真

5.1 球面插补点仿真

设球心为P0=(30，-100，100)，球心半径为R=30cm，机器人末端在空间上走的径向的半圆数m=20，每段径向半圆插补次数n=100。则根据Matlab画出的球面插补点，如图5所示。

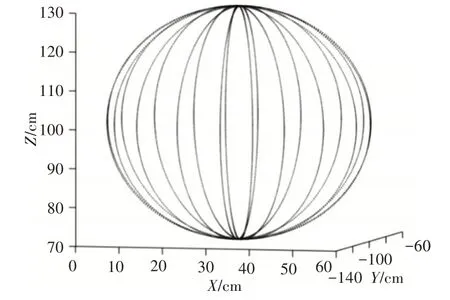
图5 球面插补点仿真图Fig.5 Spherical Interpolation Point Simulation

5.2 机器人球面插补运动仿真

通过已得到球面插补点坐标，末端姿态，球心P0=(30，-100，100)，球心半径R=30cm。使用Matlab Robotics Toolbox工具箱编程可以得到机器人球面插补运动仿真过程，如图6所示。

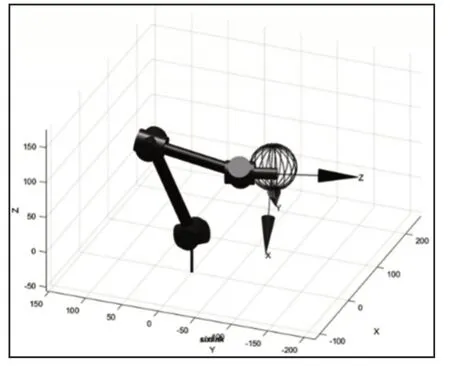
图6 机器人球面插补运动仿真Fig.6 Spherical Interpolation Motion Simulation of Robot

6 结论

（1）提出一种基于等弦分割采样的新型空间圆弧插补算法，为实现球面插补奠定理论基础。该算法根据弦长分割所求得插补点均在圆弧上，无需坐标变换，积分运算，微分运算等，简化了机器人插补过程中运算量。在Matlab中仿真并与其他常见算法进行对比，计算量大幅减小。通过样机实验，验证了上述插补算法的正确性。

（2）将这种新型空间算法应用到更为复杂空间球面插补，求解球面插补点坐标以及姿态，仿真出球面插补点。对实验室机器人进行仿真模拟出机器人在球面插补中的运动过程作出验证，实现了对不同尺寸球面插补仿真。