一种战时人力资源补充分析方法
李 旖,田 尧
(1.78123 部队,四川 成都 610031;2.78092 部队,四川 成都 610031)
关键字:人力资源补充;作战减员;系统分析;混合整数规划
1 概述
战时人力资源补充,是指参战人员发生减员(包括战伤、战死、心理问题不宜参战等)情况,通过多种运输手段,将备补人员输送至前线参战部队,对人力资源进行配强、增补、替换等。做好战时人力资源补充工作,对于提高作战效益、增强作战能力具有巨大增益作用。传统的战时人力资源补充,以简单的数学计算为主,考虑情形较为简单,备补点、运载工具、需求点等要素相互割裂,并未成系统地、成体系地加以分析。针对上述问题,本研究构建了一种战时人力资源补充系统分析框架,提出了人力资源补充模型,结合具体案例进行分析。
2 构建模型
按照参与要素划分,战时人力资源补充系统可分为需求点(参战部队)、备补点(后方部队和人力资源备补点)、运载工具(运输机、火车、货车和汽车等)、投送路线(公路、铁路和航线)和补充人员(各军兵种相关人员)。根据战时人力资源补充系统各要素的相互关系,可以刻画出系统的动态特征。
战时人力资源补充体系的目的,是为了优化补充体系结构,加快补充速度,提高补充效益。因此,模型的目标函数可以设计为整个体系运转的投送任务满足度最大或经济效益最高。目标函数(1)中DemandFulfilment 代表参战部队的人力资源满足度。
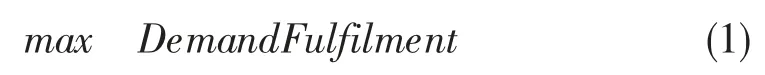
战时人力资源补充体系是否选择某个备补点i、后方部队j 作为补充调配对象,可以用约束函数(2)、(3)表示,Pi、Qj 为1 表示选择i,为0 表示不选择。

t 时刻,备补点i 原储备量XX(i,t-1),向参战部队k输送人员数量T(i,k,t),同时获得来自后方部队的有效补充R(j,i,t),用约束函数(4)表示。
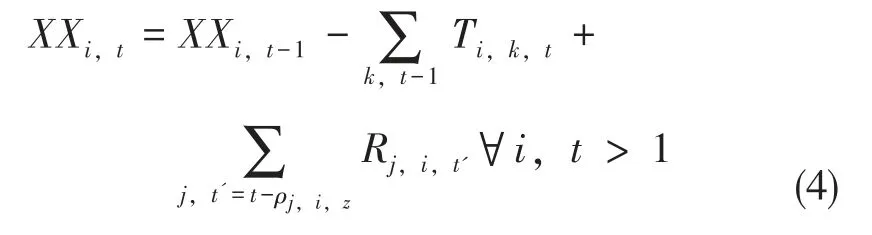
与备补点i 不同的是,除了向参战部队k 输送人员Sj,k,后方部队j 还需向备补点i 调配人力资源Sj,i,用约束函数(5)表示。
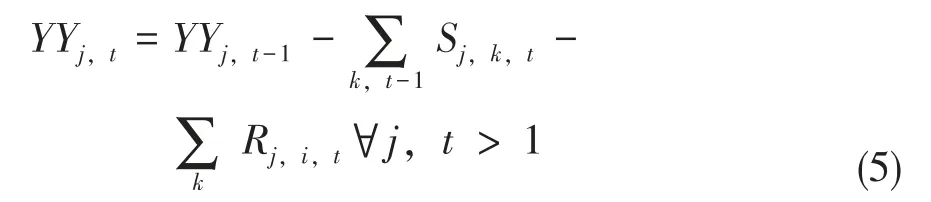
需要注意的是,t 时刻备补点i 向参战部队k 输送的人力资源数量Ti,k,t,不能超过自身的储备量XXi,t,同理于后方部队j,分别用约束函数(6)和(7)表示。

参战部队k 和备补点i 的人力资源需求满足量用Dk和Bi,未满足量用Dk'和Bi'表示,用约束(8)、(9)来描述参战部队和备补点的人力资源需求满足程度。
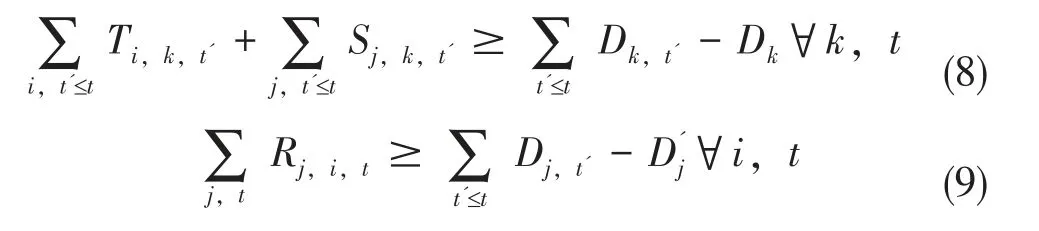
3 算例
设想一般战役作战场景,设定合理的参数值和变量值,代入上述构建的计算模型进行求解,并对计算结果进行分析。
3.1 参数设定
假定共有备补点6 个,后防部队5 个,参战部队5 个,运载工具共有2 类(包括空中投送和地面输送)。
后方部队和备补点人员最高储备数量见表1,假定各备补点和后防部队的最高储备量均相同,备补点、后防部队间的投送时间见表2,前方参战部队的人员需求量见表3。

表1 后方部队与备补点的最高储备量
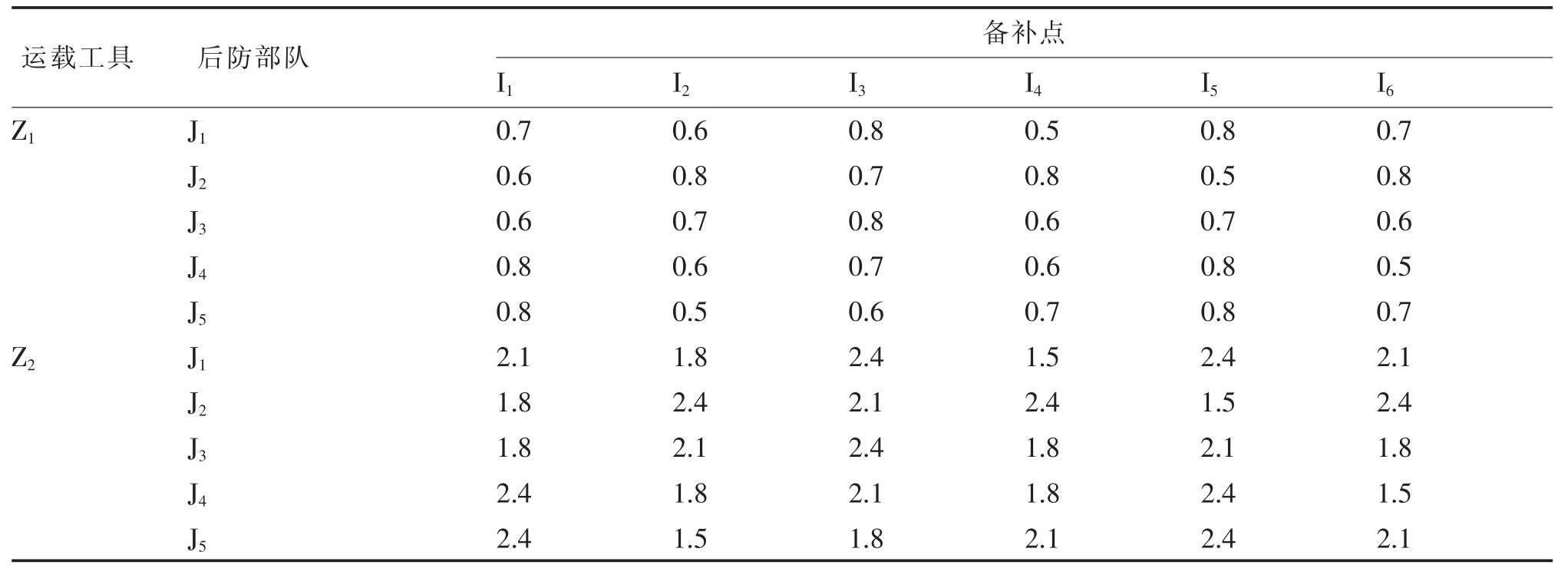
表2 后方部队与备补点之间的投送时间

表3 参战部队人力资源需求量
3.2 编程计算
上述构建的混合整数规划模型(MIPM)可应用LINGO17 进行建模计算。模型变量5562 个,其中整数变量5342 个,约束条件4992 个,经过53406 次迭代,共计28S,求得全局最优结果(Global Opt)。计算结果如图1 所示。

图1 一般战役人员补充分析模型计算结果
3.3 结果分析
经计算,参战部队的人员补充需求均得到满足。备补点和后方部队的选择见表4,5,备补点全部被选中,后方部队J2、J4、J5 作为人员提供点。参战部队的人力资源需求量较多,备补点的人员储备不足以满足前线的人员补充需求,需要调动后方部队方可完成投送任务,这种情况与计算结果相一致。

表4 一般战役备补点选择

表5 一般战役后方部队选择
在完成投送任务量方面,具体如图2 所示。备补点将自身储备人员全部派往前线,起到了承前启后的作用。后方部队承担了补充调配的大部分任务,占比高达70%。

图2 备补点与后方部队完成任务量及占比
在运输工具的选择方面,两种运载工具均使用,如图3 所示。人员补充的首要目标是保证能够快速补充到位,采用的策略是尽可能多运用备补点作为中转站进行人员调配,因此运载工具的选择上以工具Z2 为主;整个体系处于快速周转的状态,运载工具的出动频率很高,就形成了备补点派出的数量大于后方部队和备补点的情况。

图3 备补点与后方部队运载工具使用情况
4 结论展望
本文分析了战时人力资源补充系统的特点,划分参战部队、备补点、后方部队、运载工具等要素,构建了人力资源补充模型。同时对一般战役的人力资源补充问题进行分析,得出了符合作战特点本身的补充方式和具体措施,结果较为合理,并能够对补充策略提供辅助决策建议。接下来可以对模型进行进一步拓展:①对人员类型、时间变量、投送工具、人员需求等变量进行更细化、精确化描述;②引入松弛变量、灵敏参数等,进行冗余分析,改进优化模型,提高模型计算效率;③考虑引入二级备补点等变量,使模型精细程度更深。

