基于包含度的单值中智决策信息系统属性约简

陈盼盼，林梦雷

1.闽南师范大学 数学与统计学院，福建 漳州363000

2.数字福建气象大数据研究所，福建 漳州363000

1 引言

Pawlak于1982年提出的粗糙集理论[1]是一种用于建模和处理信息系统中不完备和不一致信息的重要数学工具。粗糙集模型主要是基于等价关系的一对上下近似算子的逼近。然而，在现实生活的许多问题中，由于等价关系要求严格，导致粗糙集模型无法应用。因此，文献[2]通过结合粗糙集和模糊集[3]，提出了粗糙模糊集和模糊粗糙集。同时，对于生活中的决策问题，粗糙模糊集和模糊粗糙集不能同时表示接受、反对和犹豫的程度，文献[4]将其概念推广到直觉模糊环境，提出了直觉模糊集。

作为模糊集和直觉模糊集的推广，Smarandache提出了中智集[5]的概念。中智集理论是一种新的数学工具，有助于处理不完全和不确定性问题，一个中智集包含了三个函数：隶属函数、不确定性函数和非隶属函数。这三个函数的评估程度都是相互独立的。通过结合中智集理论和粗糙集理论，文献[6]开创了一种新的混合数学结构称为粗糙中智集，并且研究了一些算子和性质。然而，从科学或工程的实际应用角度，粗糙中智集需要重新定义算子。因此，文献[7]提出了单值中智集，并给出了单值中智集的理论算子和各种性质。单值中智集是一种特殊的中智集，可以方便地用于处理实际问题[8]。由于单值中智集和粗糙集是处理不确定信息的两种不同的数学工具，为了同时利用两者的优点，文献[9]融合了单值中智集和粗糙集提出了单值中智粗糙集模型。粗糙集、中智集、单值中智集和一系列的融合模型在处理不精确信息方面起着重要的作用，并且这些模型都是建立在集合的等价关系、相似关系和广义二元等关系上，而利用集合的这些关系对实际问题进行决策时过于严苛，甚至无法进行合理的决策。因此，文献[10]利用集合的包含度对集合之间的包含关系进行度量，提出了基于包含度的粗糙集模型。目前一些专家学者也对粗糙集的包含度模型进行了推广，提出了基于包含度的直觉模糊粗糙集模型[11]。在此基础上，文献[12]提出了新的包含度犹豫模糊粗糙集模型。由于单值中智集可以看作是直觉模糊集的推广，可以方便地处理现实中的不确定性问题和决策问题。但从现有的文献发现，已有的单值中智集研究大多集中在直接对单值中智集进行多属性决策[13-14]，而随着各种信息技术的快速发展，这些用于多属性决策的海量数据中存在大量无关以及冗余信息。因此，属性约简对于单值中智集的多属性决策问题更具有实际意义。

2 单值中智集基本概念

定义1[7]设U为非空有限集合，U上的一个单值中智集͂是由U→[0,1]的3个有限子集的函数、和组 成。͂可 以 表 示 为或其中:U→[0,1]，:U→[0,1]和:U→[0,1]分别表示A͂的真实隶属函数、不确定隶属函数和虚假隶属函数，并满足

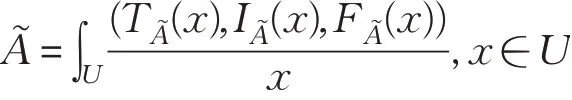
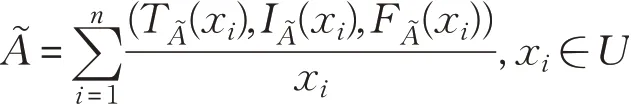
定义2[7]对任意的A͂,B͂∈SVNS(U)，有如下定义：

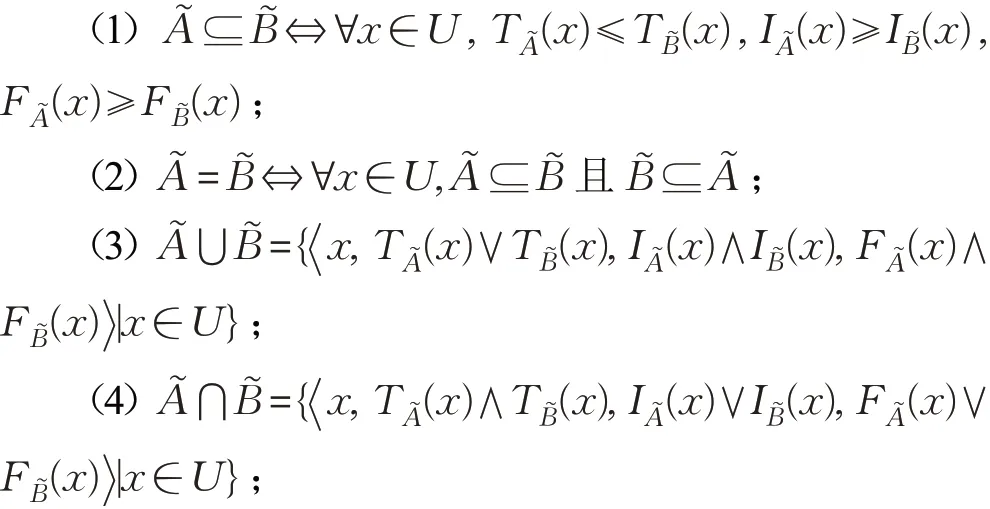
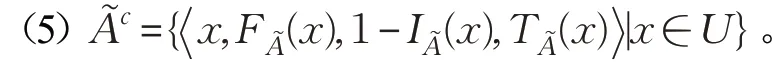
其中，“∨”和“∧”表示取最大和最小。

定理1[15]对任意的，有如下性质：

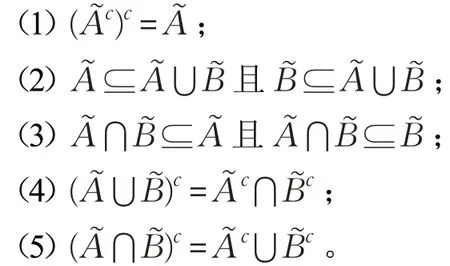
定义3[15]设U为非空有限集合，U上的一个单值中智关系定义为：

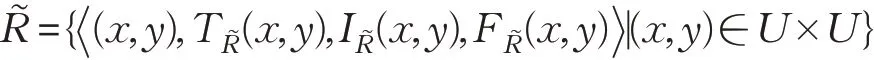
假设U={x1,x2,…,xn}，一个单值中智关系可以表示为矩阵，其中，矩阵中数对(i,j)位置表示xi和xj之间的单值中智数。

若单值中智关系R͂满足以下条件则称为单值中智相似关系：

3 基于包含度的单值中智决策信息系统属性约简

3.1 单值中智决策信息系统

定义4设U为非空有限集合，A={a1,a2,…,al}为条件属性集，表示分别由属性a1,a2,…,al诱导的单值中智相似关系，则S=(U,A)称为单值中智信息系统。若d为决策属性，则S=(U,A⋃d)称为单值中智决策信息系统。

假设论域U被决策属性d划分为U/d={d1,d2,…,dr}，故划分的决策类可表示为：

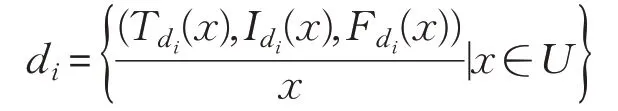
其中

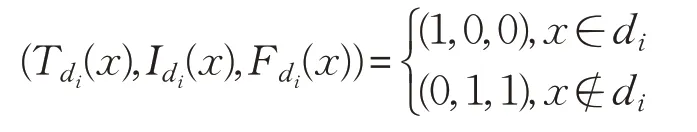
定义5给定S=(U,A⋃d),U/d={d1,d2,…,dr},表示由条件属性集A诱导的单值中智关系，∀x∈U，x的单值中智决策定义为：

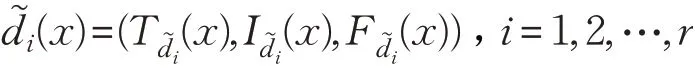
其中

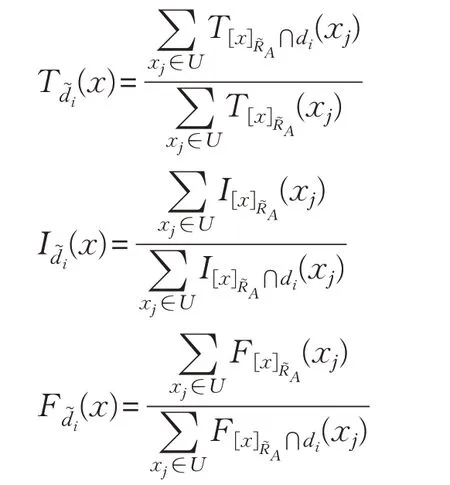
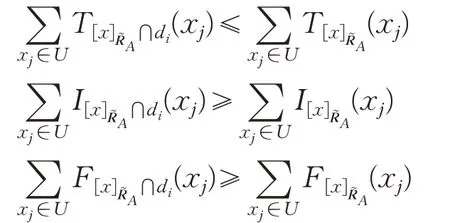
例1设论域U={x1,x2,x3,x4,x5}，条件属性集A={a1,a2,a3}，论域U被划分为U/d={d1,d2,d3}，其中d1={x1,x2}，d2={x3,x4}，d3={x5}，A诱导的单值中智关系为：

由已知有：

每个对象的单值中智相似类为：

由定义2的（4）可知：

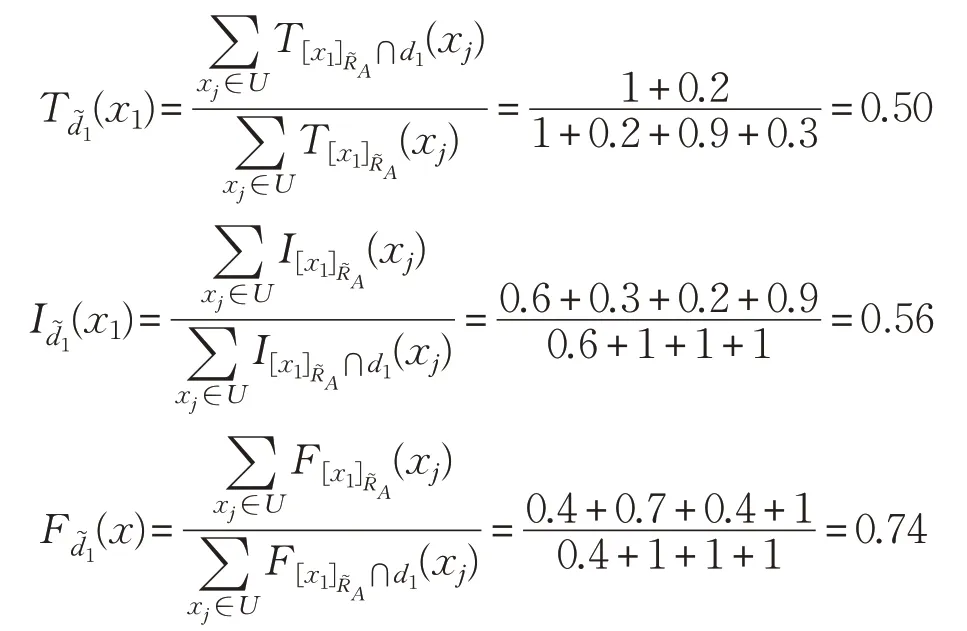
同理可求得：

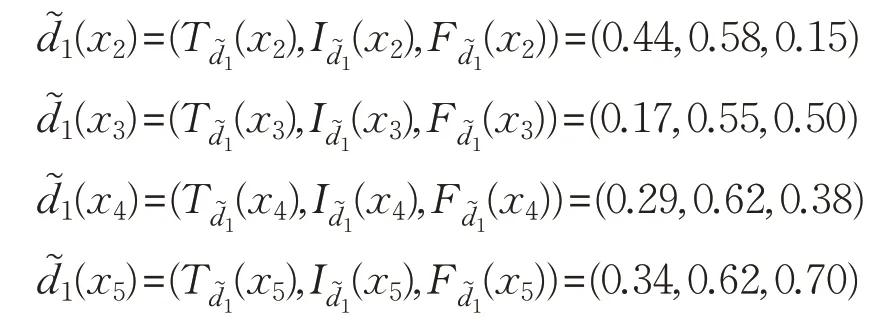
因此

同样可求得：

在应用粗糙集和模糊集理论处理生活中的实际问题时，往往用到集合的包含关系，而由于集合之间的包含关系过于苛刻，通常用集合包含度来度量。集合的包含度是集合包含关系的一种推广，是不确定理论中的一种重要度量工具。同样，单值中智集在处理生活中的决策问题时，利用单值中智包含度更有利于实际问题的解决。

3.2 单值中智包含度

定义6对于任意的A͂,B͂,C͂∈SVNS(U)，若映射D:SVNS(U)×SVNS(U)→[0,1]满足：

则称D为SVNS(U)上的包含度。

基于以上包含度的公理化定义，本文给出单值中智集包含度的两个计算公式，具体形式为：

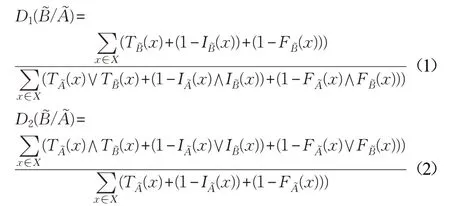
定理3公式（1）、（2）都是SVNS(U)上的包含度。

证明 以式（1）为例证明。

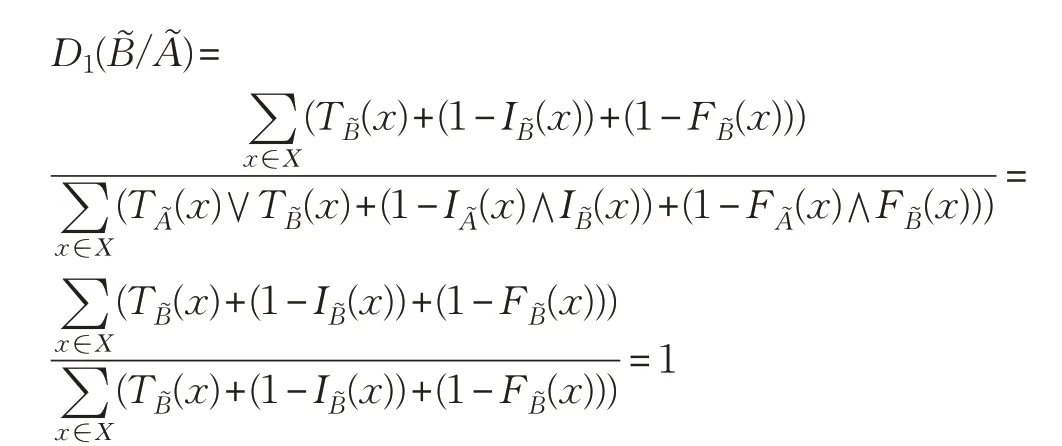
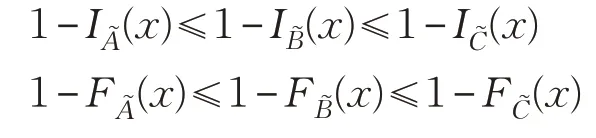
故

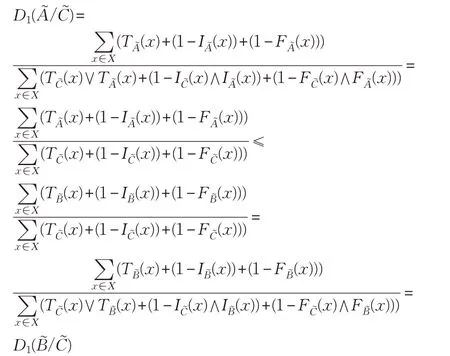
综上（1）～（3）可知，式（1）为SVNS(U)上的包含度。类似地，可以证明式（2）为SVNS(U)上的包含度。

接下来的证明和计算，均以式（1）为例进行，若采用式（2）则完全类似。

3.3 基于包含度的单值中智粗糙集模型及其性质

定义7对于单值中智决策信息系统S=(U,A⋃d)条件属性集A={a1,a2,…,al},U/d={d1,d2,…,dr}，单值中智相似关系，D为SVNS(U)上的包含度，则决策d关于B的近似空间定义为：

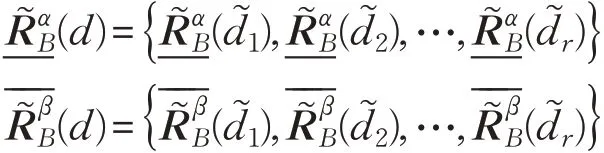
其中：

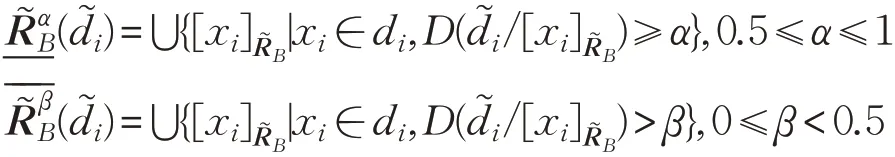
决策系统的正域定义为：

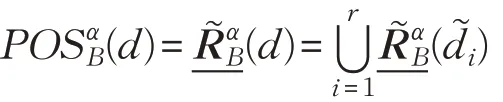
决策系统的边界定义为：

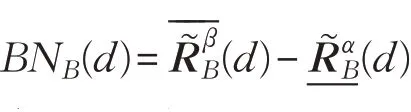
定理4设0.5≤α≤1，0≤β＜0.5，D为SVNS(U)上的包含度，则包含度近似算子满足下列性质：

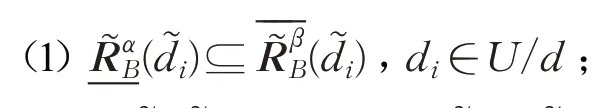
证明（1）对于任意α,β和决策类di∈U/d，由定义7可知显然成立。

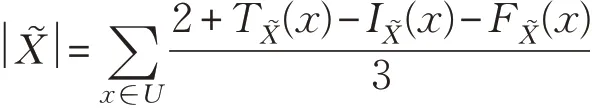
定理5对于任意的A͂,B͂∈SVNS(U)，有：

（3）同理（2）可证。

定义9给定单值中智决策信息系统S=(U,A⋃d),决策属性d对条件属性B⊆A的依赖度为：

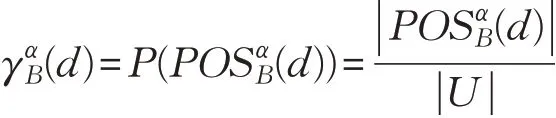
定理6给定单值中智决策信息系统S=(U,A⋃d),和包含度阈值α,B1,B2⊆A，如果，则：

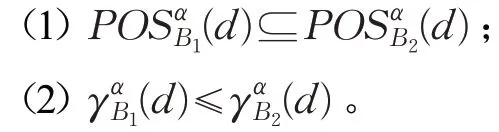
定义10给定单值中智决策信息系统S=(U,A⋃d),B⊆A，称B为该单值中智决策信息系统的约简，如果B满足：

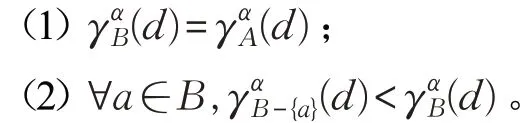
定义11给定单值中智决策信息系统S=(U,A⋃d),B⊆A且a∈A-B，单值中智属性a相对于条件属性集B的重要度定义为：

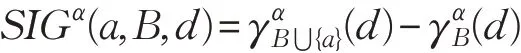
3.4 案例分析

根据定义11重要度的定义，下面给出基于单值中智正域的属性约简算法。该算法采用前向贪心搜索策略，以空集为起点，依次选择属性重要度最大的属性加入约简集中，直到增加任何属性，属性的依赖度不再增大为止。

算法1基于单值中智正域的属性约简算法

输入：S=(U,A⋃d)；

输出：约简B。

（1）初始化B=∅

（2）对任意ai∈A-B

计算SIGα(ai,B,d)=(d)-(d)

（3）选择属性ak，使其满足

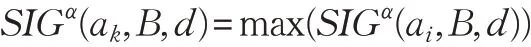
（4）if SIGα(ak,B,d)＞0

B⋃{ak}→B

返回第（2）步

else

返回B

end

根据以上算法，给出下面相应的实例进行计算单值中智决策信息系统的约简。

例2给定单值中智决策信息系统S=(U,A⋃d)，U={x1,x2,x3}，A={a1,a2,a3}，属性集诱导的单值中智相似关系分别为R͂a1,R͂a2,R͂a3，令α=0.7，且

决策属性d将论域划分为U/d={d1,d2},其中d1={x1,x2},d2={x3}，即决策为{͂}。由定义4有：

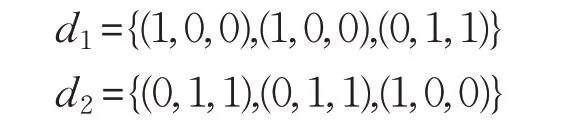
（1）根据算法1首先令B=∅，分别计算单值中智属性a1,a2,a3的重要度，对于属性a1有：

由以上定义可得：

利用例1方法有：

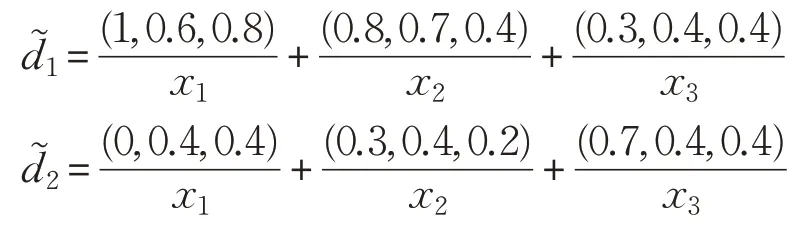
根据包含度计算公式（1）可得：

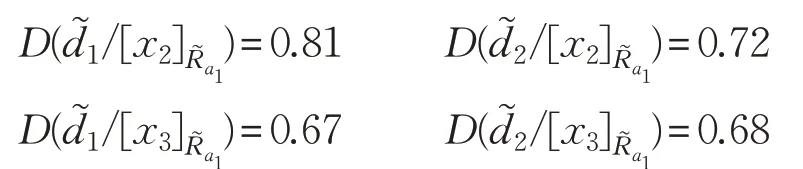
由于x1,x2∈d1,x3∈d2,且，故：

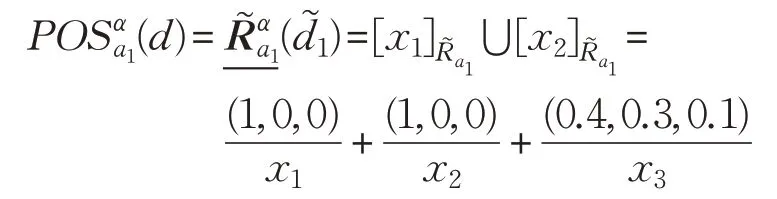
结合定义8和定义9得：

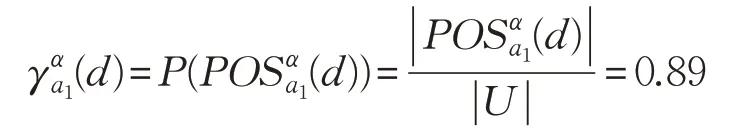
由此，SIGα(a1,B,d)=0.89。

对于属性a2有：

同理单值中智属性a1下的计算，可得：

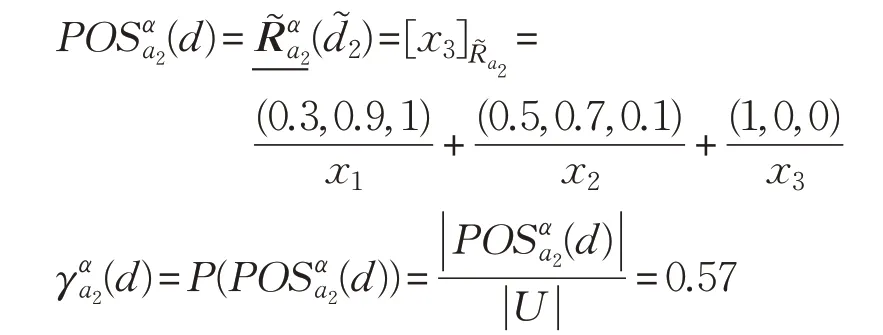
故SIGα(a2,B,d)=0.57。

对于属性a3有：

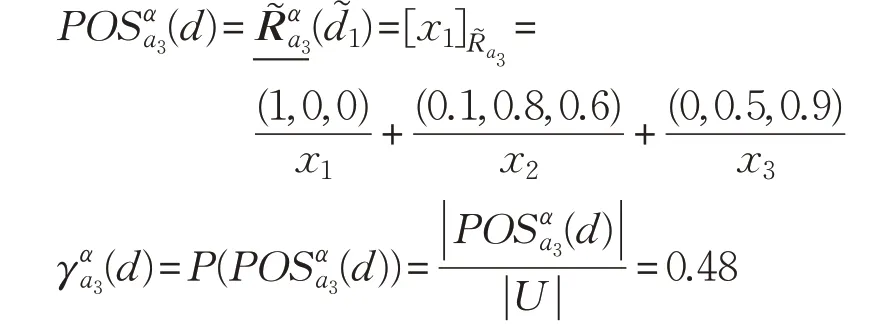
故SIGα(a3,B,d)=0.48。

（2）根据算法1的步骤（3），选择单值中智属性重要度最大的a1，令B=a1，A={a2,a3}，SIGα(a1,B,d)＞0。

同（1）可得：

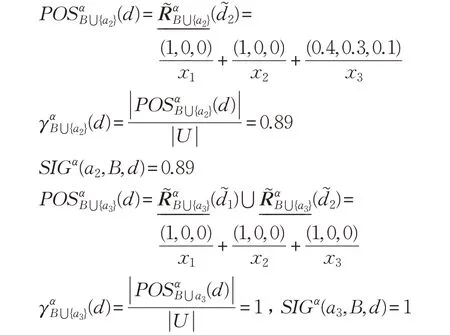
故SIGα(a3,B,d)=1-0.89=0.11,SIGα(a2,B,d)=0,因此，B={a1,a3},A={a2},由于SIGα(a2,B,d)=0,SIGα(a3,B,d)＞0。故该单值中智决策信息系统的约简为B={a1,a3}。

4 结束语

本文利用单值中智集可以同时描述真实、犹豫和非真实三方面不确定性信息的特点及集合之间的包含程度对不确定信息的度量，给出了单值中智集的包含度定义，并融合单值中智集的包含度和粗糙集进行建模，提出了基于包含度的单值中智粗糙集模型。该模型加入了变精度参数，使得在处理不确定性问题时能做出更合理的决策，同时降低问题的不确定性。最后，利用该模型对提出的单值中智决策信息系统进行属性约简。本文所提模型在处理不确定性问题方面的适用范围更强，应用领域更广泛。