织物瑕疵检测方法研究进展

田宸玮，王雪纯，杨嘉能，钱育蓉

1.新疆大学 软件学院，乌鲁木齐830000

2.中国石油吐哈油田分公司 勘探开发研究院，新疆 哈密839009

1 引言

织物是人们在日常生活中广泛使用的材料，由纺织纤维制成。纺织纤维由天然纤维如亚麻或羊毛等制成，或尼龙、人造纤维等化学纤维制成。织物瑕疵是指在工业化生产制造过程中织物表面出现的瑕疵缺陷。这些织物瑕疵主要由机器故障、纱线问题、不良加工、过度拉伸等问题引起的。严重的瑕疵问题会导致织物产品的滞销和经济损失[1]，而织物瑕疵的检测是一个旨在识别和定位这些瑕疵的质量控制过程。目前，纺织业界定的织物瑕疵有76种[2]。

在以往的检测方法中，人工检测是确保织物质量的唯一手段。人工检测的方法虽然可以做到即时纠正一些错误，但是疲劳会导致不可避免的人为错误，并且人工检测通常不会检测到较为微小的瑕疵。目前人工检测成功率仅为60%～75%[3]。因此，使用高效和稳定的计算机视觉来代替低效的人工视觉，实现织物瑕疵的自动化实时检测，具有重要的经济效益和现实意义。

目前实现织物瑕疵的实时在线检测存在以下挑战：（1）繁多的面料种类；（2）不同壁纸组的组合；（3）织物瑕疵与背景纹理相似；（4）整个检测过程效率较低。

本文根据不同的检测方法综述了瑕疵检测的研究进展，总结各个方法的优点与不足，并对未来的织物瑕疵检测研究方向进行了预测。

2 织物瑕疵检测

2.1 织物纹理图案放置规则

织物图案可以被看作是二维的纹理图案，但是并非所有的二维纹理都设计有图案。二维图案纹理由底层晶格确定，其规则由17个壁纸组控制[1]，如图1。在数学代数中，壁纸组也称为晶体组，是明确定义的。这样，不同组的图案纹理可以通过平移、旋转、反射、滑动镜像反射构成。这17组命名为p1、p2、pm、pg、cm、pmm、pmg、pgg、cmm、p4、p4m、p4g、p3、p3m1、p31m、p6和p6m，命名规则完整符号以p（Primitive cell）或c（Centred cell）开头，接数字n表示旋转对称的最高阶：1倍（none）、2倍、3倍、4倍或6倍。后两个符号表示相对于该图案的一个平移轴的对称性；如果有一个垂直于平移轴的反射面，则选择此轴为主轴（如果有两个满足条件的平移轴，则选择其中一个轴）。符号m（mirror）代表镜像，g（glide reflection）代表滑动，1（none）则代表无操作。

2.2 织物纹理图案放置规则

有两种定义检测成功率的方法，一种被定义为：

式中，样本包括有瑕疵样品和无瑕疵样品。

可以进一步定义检测率和误检率：

另一种检测成功率定义为：

式中，TP、FP、FN和TN的定义如表1所示。

表1 瑕疵检测中真阳性，假阳性，真阴性，假阴性的定义

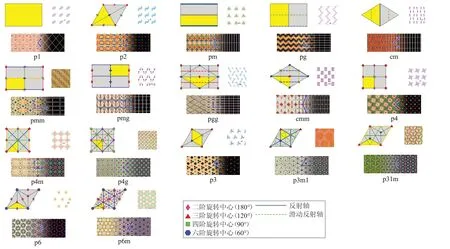
图1 17个壁纸组

根据目前的织物瑕疵检测方法分析，以下因素会影响检测成功率：（1）瑕疵本身与纹理表面相似；（2）瑕疵检测算法的复杂度；（3）照明：根据不同颜色的纺织品通过单色光照射可以更好地提取瑕疵特征；（4）图像采集方法：在使用数码相机采集的技术上使用红外、X光照射以及采集热成像后的织物图像。这些方法可能会在瑕疵检测中提高检测效率或检测率。

3 织物瑕疵检测方法

根据对图像处理原理的不同，分为以下四类：基于结构的方法、基于统计的方法、基于频谱的方法以及基于学习的方法，如图2所示，其中混合方法为基于以上四种方法的组合，并行方法旨在加速整体过程。本文主要对近几年织物瑕疵检测算法的最新研究进展进行分类探究和分析，列举各个方法与同类方法的不同之处，比较分析各种算法的优劣势。

3.1 织物纹理图案放置规则

基于结构的方法通常是将纹理视为纹理基元的组合，织物图案的纹理通过纹理基元的一些简单的放置规则组合来实现。纹理的结构分析主要由纹理放置规则的判断以及纹理元素的提取。

针对单一方向单一尺度下特征提取不明显的问题，Dhivya等[4]使用多方向多尺度的方法提取织物瑕疵的边缘图，轮廓特征由KNN分类器提取和分类，结果表明该方法较SVM、RBM和ELM产生了更好的性能结果。同样是在轮廓提取的过程中，孙波[5]在图像平滑处理时，通过迭代次数的增加，使得平滑图像中的织物纹理逐渐变淡，同时织物图像的细节得到较好的完整保留。显著纹理背景下因灰度级有限、对比度不明显导致织物图像疵点检测难度较大，针对此问题，石美红等[6]基于显著纹理特征进行了疵点检测，提出一种多尺度度量局部纹理粗糙度的自适应算法，首先计算局部纹理粗糙度特征的显著度(fc)：

式中，hn为灰度值n在图像中出现的频率。Sbest为最佳窗口的尺寸。

此算法的局部纹理粗糙度均值变化曲线是线性递增的，结合织物图像的视觉显著性分析，瑕疵与背景间的纹理区域灰度对比度有着明显的差异，根据局部纹理粗糙度定义对比度特征(fm)：

式中，g为最佳窗口下的灰度均值。

为进一步提高局部纹理的显著性特征，使用区域局部纹理最佳窗口的视觉显著性度量方法，根据最佳窗口计算方向特征(fd)：

式中，χ2表示卡方统计；是对四个方向边缘相应的二进制编码D进行灰度直方图统计得到的特征向量，其定义为：

式中，fij表示以(i,j)的像素点为中心，以Sbest为窗口大小的子图像；*为卷积运算；Tk为同等窗口大小的算子模板；；为平均特征向量，其计算公式为：

对每个特征子图进行归一化处理，然后据式（5）～式（7）按照式（10）加权融合得到视觉显著性特征图FR：

式中，ω1=(1-)2,为对应每个特征子图上除全局极值点后剩余点的平均值。

Zhu等[7]结合自相关函数的方法确定了织物图像的图案周期之后使用欧几里德距离来辨别有无瑕疵。自相关函数是提取信号周期的重要方法，它描述了随机信号在两个不同时刻之间的自相关程度，由于色纱在经纱和纬纱两个方向上的密度和布局不同，在两个方向上的周期也不同，定义纬纱方向(Cx,0)和经纱方向(C0,y)的自相关函数如下：

图2 织物瑕疵检测方法分类

式中，x=1,2,…,M,y=1,2,…,N,M和N为图像的宽度和高度，G(i,j)是像素坐标(i,j)的灰度值。由式（13）可求出，R G和B代表RGB颜色模型中的三个组件。

GLCM的欧式距离D定义如下：

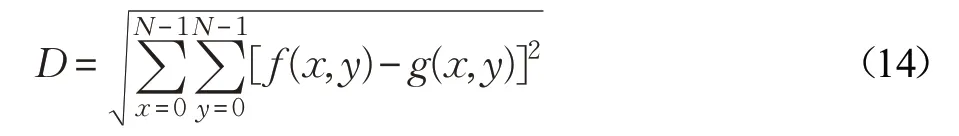
式中，f(x,y)表示待检测图像的GLCM，g(x,y)表示模板图像的GLCM，N表示图像的灰度，D值越小代表两个图像越相似。

自相关曲线的周期为纹理基元的大小，根据式（11）、（12）计算得到结果如图3所示，可看到该图像的纹理周期为26个像素（该图像为256×256像素的图像，通过人眼观察每行有20个方格，256/20×2=25.6≈26）。

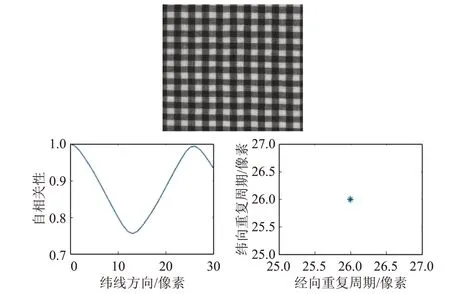
图3 织物瑕疵图像及其自相关函数周期

由于瑕疵会破坏染色织物的周期性，所以采用无瑕疵织物来提取织物的图案周期。该方法用于组织周期较小的色织面料时得到了较高的检测精度且拥有更好的适应性。检测出的目标瑕疵具有较好的一致性和完整性，可用于具有显著纹理背景的织物表面的瑕疵检测。织物瑕疵图像的显著性检测思想是将瑕疵区域定义为显著区域，其余纹理图案部分定义为低显著性区域。同样使用显著性检测的思想，李倩倩等[8]利用上下文的特点同时结合主成分分析法（PCA）对图像信息进行降维，结合Otsu阈值分割法分割瑕疵区域，能较好地抑制织物花纹背景对瑕疵检测的影响，分割出断头疵、破洞、跳花、污渍和打结五种类型的瑕疵。根据织物表面的结构性纹理特点，吴军[9]在分割阶段把采集图像分成大小两个窗口，在大窗口下将样本图像分解成经向子图和纬向子图，若检测无异常则进行小窗口下小波分解，从而识别出各类含有瑕疵的图像。

3.2 基于统计学方法的织物瑕疵检测

统计方法使用统计量来提取纹理特征，使用该特征描述织物纹理之间的相异性以及织物纹理整体结构的一致性。基于统计方法的疵点检测主要有：灰度共生矩阵、数学形态学、直方图统计法等方法。

3.2.1 灰度图像以及灰度共生矩阵

灰度图像中灰度急剧变化的区域通常是图像的边缘信息，借此吴军[10]基于灰度分布梯度，结合织物表面的结构性纹理特点，使用直方图均衡化增强灰度图像的对比度，针对数据处理量较大的问题，采用全值阈值法将灰度图像转成二值图像。该检测方法能较好且快速判断有无瑕疵，适应瑕疵范围广，对于经、纬向等方向类瑕疵、块状区域类瑕疵较明显，但对于棉球等点状类小瑕疵则检测效果不理想。灰度共生矩阵（GLCM）是通过研究灰度的空间相关特性来描述纹理的常用方法，在纹理分析、图像质量评价方面都有很重要的作用，原理如图4。

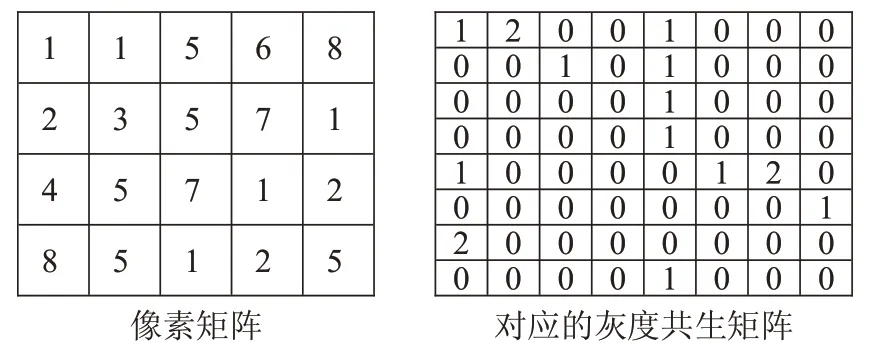
图4 像素矩阵以及灰度共生矩阵

图4 左侧图像为一个共有8个灰度级别的图像，数字代表灰度级，右侧是其对应的灰度共生矩阵。灰度共生矩阵坐标(x,y)值为n表示在像素矩阵中，在水平方向上，灰度值x的像素右侧相距一个像素值的像素灰度为y的个数有n个。

更改上述的方向以及距离可得到不同的灰度共生矩阵。总结来说，如图5所示，有四种不同方向的灰度共生矩阵。

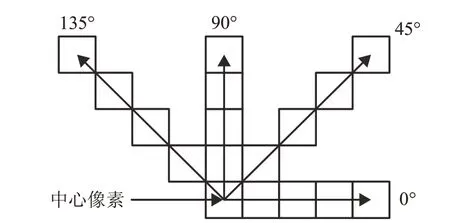
图5 灰度共生矩阵方向

Arnia等[11]提出了一种检测框架用于检测使用离散余弦变换（DCT）压缩后的图像，不同的压缩系数可以检测出不同的瑕疵类型，检测结果如图6所示，由于减少了计算量，故此方法比较适合于织物瑕疵的实时检测。

图6 文献[11]方法检测效果图

区别于传统线性构建GLCM的方式，董蓉等[12]根据灰度出现的概率进行量化，通过最优尺度方向学习获得参考非线性GLCM特征向量和自适应的二值化阈值，之后使用最优尺度方向参数进行非线性GLCM特征提取，并与参考特征向量匹配来定位瑕疵。该方法很大程度上凸显了瑕疵区域和非瑕疵区域，同时GLCM本身对噪声有很强的抗干扰能力，再结合自适应的二值化阈值，使得图像在未进行形态学滤波的情况下，也能准确地定位瑕疵区域。使用灰度图像以及灰度共生矩阵的各个文献所检测的瑕疵类型以及实验结果如表2所示。

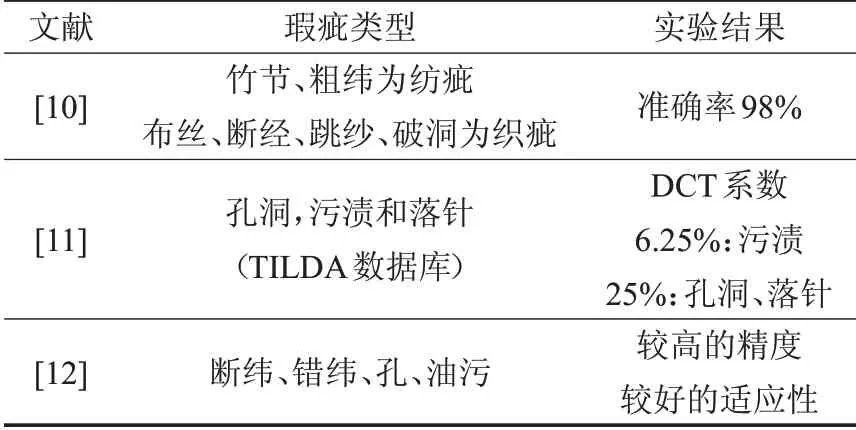
表2 灰度图像以及灰度共生矩阵方法比较

使用灰度共生矩阵的方法依据其特性可以使用不同的统计特征来表示记录各个像素之间的空间关系，不过多种的统计特征虽然可以保持较高的准确率但是随之的较大计算量不利于确定最优的偏移向量。但是相较于小波特征或者局部二值模式来说，灰度共生矩阵基本不受噪声影响，二值化后的结果不需要使用形态学滤波方法进行滤波。

3.2.2 数学形态学

数学形态学的操作有二值形态学和灰度形态学两种。腐蚀和膨胀是数学形态学的两个基本操作，二者通过结合又形成了开运算和闭运算。现阶段，基于形态学的图像处理已经成为图像处理比较核心的领域。

相比于Gabor滤波器，数学形态学在参数设置方面没有较高的要求，基于此特性，Jing等[13]根据形态成分的不同分离图像符号，保持了每个成分的信息，确保更精准的织物瑕疵定位。相同条件下，该方法检测率高于Gabor滤波器的检测算法。该方法不仅可以识别噪声还能保留瑕疵的信息和形态特征。检测结果如图7所示。

Rebhi等[14]基于局部同质性和数学形态学的方法设置以Ic(xc,yc)为中心，宽度为(2N+1)的方形窗口P，在窗口P中可以定义从中心像素到像素Pi的不同矢量：

图7 文献[13]方法检测效果图

式中，(xi,yi)是像素Pi的坐标，(xc,yc)是中心像素Pc的坐标，i是一个整数，范围：

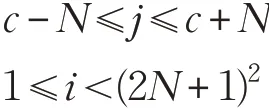
式中，N是一个整数，用来定义窗口P的大小。

图8是当N=2时，根据中心像素与周围任意像素连接的矢量Pi,c，向量fi定义为：

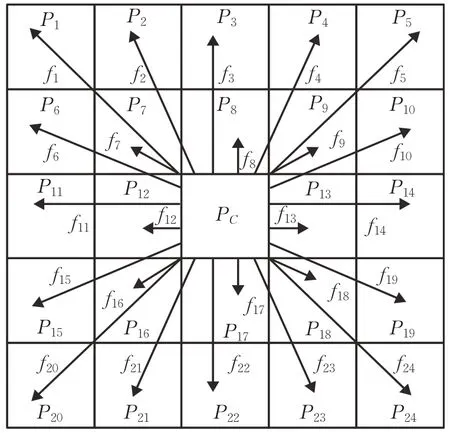
图8 用于计算5×5掩模的局部均匀性不同的矢量f i

首先使用开运算和闭运算尽可能消除织物图像中的纹理背景，再结合方形结构元素来提取织物瑕疵。因织物瑕疵种类繁多以及瑕疵尺寸的不确定造成检测效果差的问题，张波等[15]使用一种基于相对总变差模型和灰度自适应的数学形态学的方法，先通过相对总变差模型对纹理进行去除以及纹理与瑕疵的分离，再使用灰度自适应数学形态学对图像进行增强，针对瑕疵多样性以及尺寸不一的问题，该方法提高了不同瑕疵提取以及检测的通用性。区别于此，何峰等[16]使用一种窗口跳步形态学方法对织物图像进行腐蚀操作，通过瑕疵连通区域来确定瑕疵大小。检测效率较快速傅里叶变换特征点算法以及传统形态学算法相比有了很大的提高，实际工业生产环境下，实时检测速度超过80 m/min，疵点检测精度大小为0.1 mm，满足实际生产需求。使用数学形态学的各个文献所检测的瑕疵类型以及实验结果如表3所示。

数学形态发虽然较一些基于频谱分析的方法有较低的要求以及更好的效率，但是数学形态法的优点只有在织物纹理图案不具有周期性的前提下才能表现出来，也就说明了数学形态学的方法不适用于具有周期性纹理的织物图像。

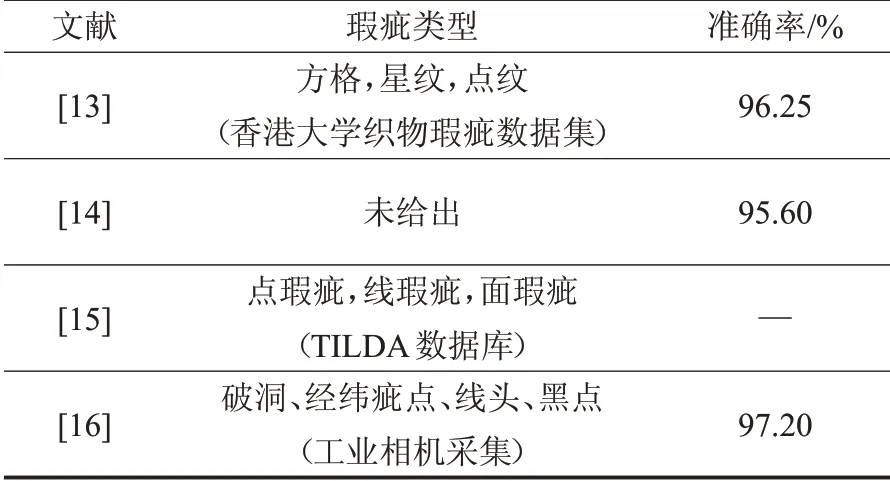
表3 数学形态学方法比较

3.2.3 直方图统计法

2.学业成绩测量。经查阅大量文献[1][2][3]，可知学生学业成绩的测量都以月考、期中、期末等大型考试中的语文、数学、英语三科的总分加权平均，即可当做学生的学业成绩。本调查中也采取相同的学业成绩认定方法，以七、八、高一、高二四个年段于同一时间测试的第一次月考成绩为参照标准。

直方图是一种质量分布图，可以展现灰度图像像素分布的情况。李春雷等[17]提出的应用方向梯度直方图（HOG）和低秩分解的织物瑕疵检测算法，将疵点图像均匀分块后提取HOG特征，取每块的这些特征作为该块的特征向量，特征提取分为四个步骤：Gamma校正、计算图像梯度、构建梯度直方图、组装HOG特征，将所有的特征向量组合成特征矩阵进行低秩分解，得到一个对应于背景的低秩矩阵和对应于瑕疵的稀疏矩阵，通过稀疏矩阵生成显著图。可以较好地将瑕疵与背景分离开，检测效果如图9所示。

另外，此方法刚开始均匀分块后的提取特征步骤如果是应用在实时检测方面可以考虑使用一些并行的方法来提高实时检测的效率，该方法为进一步研究在实时检测中应用提供了新的思路。

3.3 基于频谱分析方法的织物瑕疵检测

基于频谱分析的织物瑕疵检测方法是根据织物纹理基元的周期性与频谱特性相似的原理，将织物图像从空间域转换到频域后进行检测。

3.3.1 傅里叶变换

傅里叶变换具有较小计算量的特点。任何频率和幅度的正弦和余弦信号可以由傅里叶变换的总和表示，当傅里叶变换应用于一维空间中的图像时，空间方向相等，在连续形式中，傅里叶变换由二维给出：

式中，w1,w2是定义空间频率的频率变量，F是复值函数。

Yildiz等[18]在其实验中使用热像仪获取的图像作为输入图像来检测织物瑕疵并使用基于快速傅里叶变换（FFT）的算法，利用无瑕疵部分和瑕疵部分之间的热差异使得瑕疵部分变得明显这一特性来检测织物瑕疵。

傅里叶变换最明显的优点就是在于其提取的图像特征是频率分量，而这些频率分量在图像的缩放旋转等操作中不会改变。表明无法在空间域上定位织物瑕疵。

3.3.2 小波变换

小波变换的优点在于其可以使用不同的子小波来识别不同的织物瑕疵类型，并且在对原始图像进行压缩后也能保留较为完整的信息。较高的准确率同时也意味着成本较高。

3.3.3 Gabor滤波器

Gabor滤波器是一种边缘提取的线性滤波器，与人类视觉的频率和方向表达很像，所以很适合纹理的表达和分离。

针对具有周期性纹理的织物，Zhang等[20]基于总距离匹配函数和最优Gabor滤波器组的织物瑕疵检测模型，滤波器参数θ采用二进制粒子群算法（BPSO）进行优化，对于方向参数，目标函数由两个Gabor滤波器组成的滤波器组卷积的正常织物图像的能量及均值和方差组成，最后精确地分割瑕疵图像，获得了较之前同类型方法更清晰的图像，检测效果如图10所示。

图10 文献[20]方法检测效果图

Kang等[21]提出了两种检测印花织物的方法，一种是借助遗传算法来选择最佳Gabor滤波器的参数，另一种利用距离匹配来确定印花织物的单位。最优Gabor滤波器可以去除织物背景噪声并增强瑕疵信息，从而可以完成瑕疵分割。Gabor滤波器在检测不规则织物方面具有更好的性能。距离匹配方法在测量织物周期方面有较好的效果，Zhang[22]使用频率滤波将织物纹理和图案纹理分离，根据距离匹配函数来确定纹理的周期。Qu等[23]在瑕疵检测算法中主要包含训练和检测两个过程，根据图像的纹理周期，设置Gabor滤波器参数，当检测时，检测的织物图像首先通过两个不同尺度的Gabor滤波器进行处理。然后通过下采样处理进行大规模图像，再利用局部对比度归一化操作获得的特征，计算特征与标准的距离。通过融合两个尺度的检测距离，得到最终结果，相比于单一尺度检测算法有更低的计算量。利用复合差分演化（CoDE）优化Gabor滤波器参数，Tong等[24]对于给定的图像i(x,y)和一个k×k的Gabor滤波器掩模，通过卷积运算获得Gabor滤波输出，如式（18）所示：

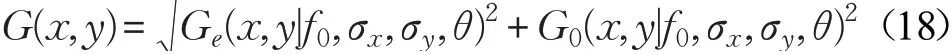
式中，G(x,y)是特征图像，是由平方非线性算子得到的，代表了滤波图像的局部能量值，特征图像在很大程度上依赖于参数，f0,σx,σy,θ的选择，这些参数提供了足够的自由度来设计具有各种形状、方向和频率特征的滤波器。

该优化问题是根据织物瑕疵和标准织物的特点设计的，实现织物瑕疵的最优特征提取。在Gabor滤波器优化中，对于每种类型织物，都需要一个无瑕疵织物图像if(x,y)和一个瑕疵图像id(x,y)，使用式（18）获得的特征图像分别用If(x,y)和Id(x,y)，这两个特征图每一个都被划分成p个不重叠的像素块，然后得到每个块的平均值和方差：

在这些像素块中，确定最大平均值和最小平均值，当输入图像被一个最佳的Gabor滤波器过滤时，瑕疵的响应将得到增强。所以，在Id所有的像素块中，umax对应的像素块是有瑕疵的，umin对应的像素块是无瑕疵的，为实现对瑕疵和无瑕疵区域的最佳区分，定义适应度函数为：

式中，S源自Fisher距离，最大的值产生最佳的分割效果，为使滤波后的方差尽可能低，采用的最终目标函数为：

结合阈值和融合操作，最优Gabor滤波器可以成功地分割原始图像背景中的瑕疵。使用最优滤波器而不是滤波器组显著降低了检测模型的计算成本。由于采集设备的原因，导致某些微小的瑕疵检测过程中会出现不连续的边缘，之后的学者可关注此方面。同样使用代替滤波器组的方法，为提高训练过程的性能，Li等[25]使用由随机漂移粒子群优化算法（RDPSO）确定的最优椭圆滤波器（EGF）代替最优滤波器。Jing等[26]使用两种基于Gabor滤波器和黄金图像相减法的方法。两者主要差别在于Gabor滤波器的选择上，第一种方法使用1 Hz中心频率和90°的Gabor滤波器，而第二种方法使用遗传算法自动选择最优Gabor滤波器。加上小波变换的黄金图像相减法。本文对比三种方法进行了比较，同时，在真实机器视觉检测系统中对上述三种方法的性能进行了测试，所提出的使用基于遗传算法确定Gabor滤波器和黄金图像相减的方法可以满足纺织行业的实际需求且较其余两者有更好的准确率。Chen等[27]将半峰值切线方法应用于Gabor滤波器的设计中以尽可能地覆盖瑕疵的频率，通过方向掩模选择两个最佳取向，并根据信噪比确定每个最佳取向的最佳尺度。但是作者提出的方法在织物损坏或者瑕疵区域与正常纹理颜色相近时，不能完全检测出瑕疵。王传桐等[28]结合非线性降维的等距映射算法（Isomap）以保持数据在空间中的几何结构，为了消除冗余信息以提高分类器的分类精度和瑕疵的检测精度，并对高维特征向量进行降维。使用Gabor滤波器的各个文献所检测的瑕疵类型以及实验结果如表4所示。

表4 Gabor滤波器方法比较

采用Gabor滤波器也是近期较多学者用来检测织物瑕疵的方法，Gabor滤波器的频率和方向决定了滤波器的大小和处理图像的位置，比较适合对织物纹理结构进行描述和分析，并且提供最佳的瑕疵检测空间域和频域，拥有较强的实用性，但是以上所有方法的前提都需要在选取了最优参数的最佳滤波器的基础上，但是最优滤波器的参数的选取较为困难且计算量较大。对于瑕疵区域与背景织物不同的织物有较好的检测性能。

3.4 基于学习的织物瑕疵检测

近年来随着计算机技术的发展，大多数行业包括纺织业都向着智能化方向改变，因此，基于学习的一些自动化方法也越来越受欢迎。并且，随着近几年深度学习的兴起，在织物疵点检测方面的应用也是越来越多。

神经网络具有映射任意复杂非线性关系的能力，Li等[29]使用一种紧凑的卷积神经网络结构，用于检测一些常见的织物瑕疵，所提出的架构使用具有多层感知器的若干微架构来优化网络。微架构的主要组成部分使用多尺度分析、滤波器分解和减少参数的技术构建，以提高紧凑模型中的检测精度。所提出的网络模型尺寸更小且在检测精度方面取得了优异的性能。同样使用多尺度分析的方法，Yapi等[30]使用监督学习利用多尺度轮廓波图像分解的统计建模来获取纹理特征，之后使用贝叶斯分类器（BC）进行瑕疵检测。该方法能够在纺织品纹理中实现高度精确的瑕疵检测和定位。Li等[31]使用基于Fisher准则的堆叠去噪自动编码机（FSCDA）由四个隐含层和一个softmax分类器组成。训练分为预训练和精调两阶段的方式进行。训练集是根据行业相机捕获的图像绘制构建的。每个去噪自动编码机（DA）都以不受限制的方式进行训练且DA的权重和偏差参数用于初始化FCSDA而非使用随机值。Rebhi等[32]利用局部同质性和神经网络检测织物瑕疵。首先计算一个新的同质性图像，然后利用离散余弦变换（DCT）于此图像并提取每个DCT块的不同代表性能量特征，这些能量特征将用于反向传播神经网络来检测织物瑕疵，检测效果如图11所示。

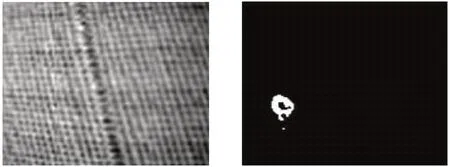
图11 文献[32]方法检测效果图

使用同样数据集的Abid等[33]使用织物纹理的多项式插值方法检测织物瑕疵，利用适当的插值多项式逼近不同的有瑕疵和无瑕疵图像区域，然后使用这些多项式的系数用于训练神经网络以检测和定位瑕疵区域。

Gao[34]研究了使用深度学习检测织物瑕疵的问题。提出了一种具有多卷积和最大汇聚层的卷积神经网络，在此网络中使用三个卷积层来提取不同的判别特征，为了减少参数规模，在池化层中激活功能后的特征映射被下采样为较小的特征映射。Zhang等[35]使用基于YOLOV2的方法，对比YOLO9000、YOLO-VOC和Tiny YOLO构建织物瑕疵检测模型。通过对比研究，选择YOLO-VOC，通过优化网络的超参数进一步进行模型改进。Yapi等[36]使用学习的方法是使用冗余轮廓变换（RCT）的织物图案统计表示。利用广义高斯（MOGG）的有限混合模型模拟了RCT系数的分布，该混合模型构成了区分有瑕疵和无瑕疵织物的统计特征。检测瑕疵区域和无瑕疵区域使用标记的织物样本训练贝叶斯分类器（BC）。Shuang等[37]使用无监督的基于学习的自动检测和定位织物瑕疵的方法，利用卷积去噪自编码网络在多个高斯金字塔层次上重建图像块，并从相应的分辨率通道合成检测结果。该方法只用少量无瑕疵样品进行培训，故利于无法收集大量织物图像的情况。同样使用无监督学习的方法，Susan[38]重新定义熵的异常值，并用它成功地定位高精度的纹理中的瑕疵或异常。通过高斯混合熵建模，自动化地找到瑕疵的最佳窗口大小。Tong[39]针对织物纹理复杂、瑕疵较小的织物，提出了一种由图像预处理、图像恢复和阈值操作组成的织物瑕疵检测模型。图像预处理提高了图像对比度，使瑕疵细节更加突出。在学习子词典的基础上，采用非局部集中稀疏表示模型对输入图像的无瑕疵版本进行估计，使可能的瑕疵可以通过阈值运算从估计图像的残差图像和输入图像中容易地分割出来。有瑕疵的织物图像通常由一个相对一致的背景纹理和一些稀疏的瑕疵组成，Cao[40]在一定的特征空间中将这些瑕疵表示为一个低秩矩阵加上一个稀疏矩阵。提出一种求解效率较高切基于最小二乘回归的子空间分割模型。吴莹[41]采用K-奇异值分解 KSVD）的方法训练得到一个自适应字典。利用该字典用于机织物纹理表征，重构正常的机织物纹理图像。在此基础上，采用阈值法检测织物瑕疵，其鉴别能力明显优于离散余弦变换（DCT）字典。使用基于学习的各个文献所检测的瑕疵类型以及实验结果如表5所示。

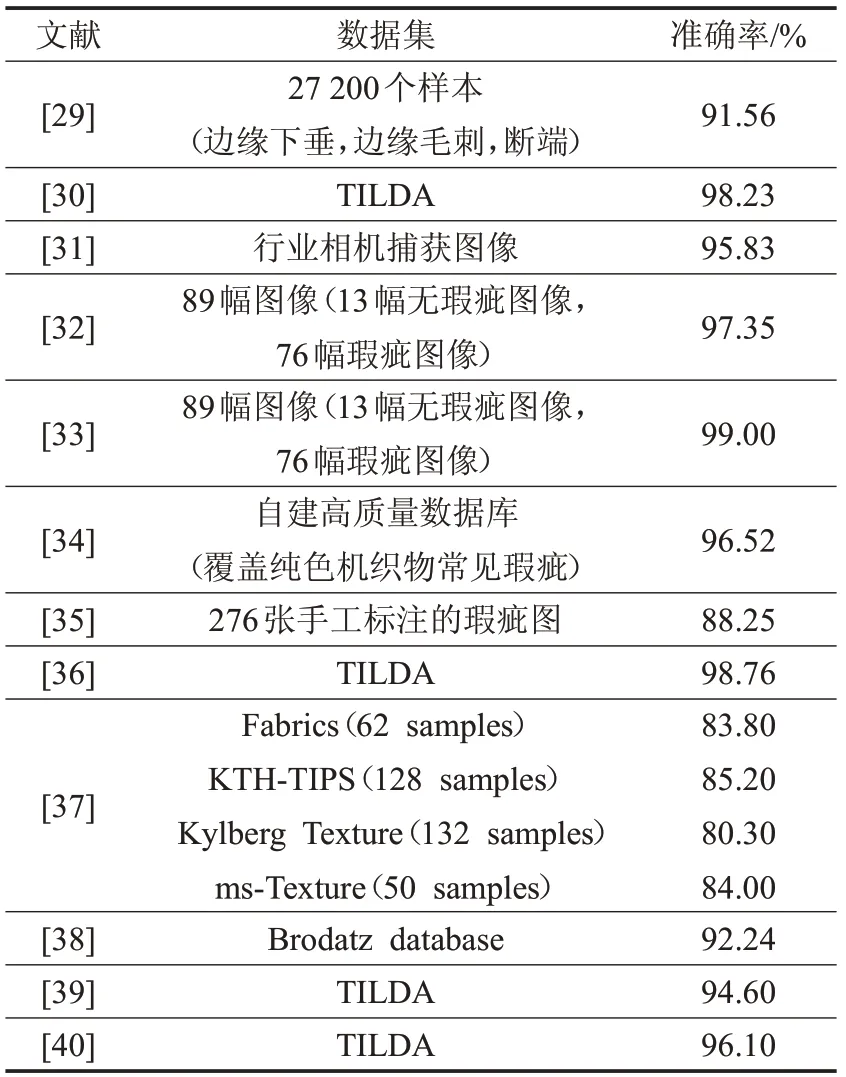
表5 基于学习方法比较

虽然学习的方法可以很好地拟合大量具有输入特征的非线性数据，但是多层的神经网络需要调整大量参数。即使擅长图像分类的深度学习，也并非是一个通用的分类技术。

3.5 混合方法

有色的织物采用相近的颜色光照射可以获得更好的结果，Bandara等[42]结合形态学运算和阈值的算法应用于织物瑕疵的特征提取，结果表明根据织物颜色使用相近颜色光照射可以更好地提取瑕疵特征，最后作者提到使用紫外线照明在检测油脂瑕疵时比其他照明更有效。所以，针对某些瑕疵使用一些非常规的图像采集方法可以更容易地分割瑕疵区域。Zhang[43]使用结合局部二值模式（LBP）和灰度共生矩阵的方法，使用LBP提取图像的局部特征信息，通过GLCM描述图像的整体纹理信息。最后，将两部分的特征信息作为BP神经网络的输入对瑕疵进行分类。Li等[44]采用金字塔小波算法对样本图像进行处理，分割图像使用基于最大期望的高斯混合模型获得了较好的分割效果。

织物瑕疵检测是一个多步骤的过程，针对每个步骤又有很多的方法可以使用，但是，在提高某些步骤准确率的同时需要考虑整个过程的效率是否会受影响。

3.6 图像处理中的并行方法

在织物瑕疵检测过程中的一些并行的方法，如：织物瑕疵的边缘检测可以使用并行的算法提高检测效率，王浩等[45]在GPU平台上提出基于统一计算架构（CUDA）的并行算法，实现了Retinex图像增强算法的并行处理，较串行算法速度提高了40倍，同样的平台，张晗等[46]为提高地质图像边缘检测算法的计算速度，对大尺寸的图像加速比可提高120倍以上。这为之后相关实验提高检测效率方面提供了新的思路。

4 结束语

随着科技不断的更新迭代，新的理论与方法不断被学者们提出来。本文总结了近年来织物瑕疵检测的一些主流方法，这些方法对应的文献以及优缺点如表6所示，但是，目前织物瑕疵检测的实时在线检测还面临巨大的挑战。结合目前的研究现状，未来织物瑕疵检测的问题将在以下几个方面展开：

（1）瑕疵检测算法的通用性。尽管不断有新的理论与方法被应用于织物瑕疵检测，但是大多数的理论与方法都只被应用于个别种类的瑕疵检测。但是，所有种类的织物都被分类为17个壁纸组。无论织物图案或纹理出现多么复杂，它都必须属于17个图案组中的一个。这大大降低了自动化织物检测方法的开发和验证的难度，为织物图案组开发的方法和结果应该具有共同的特征和属性。这种分类有助于处理纺织工业和市场中可用的各种织物。

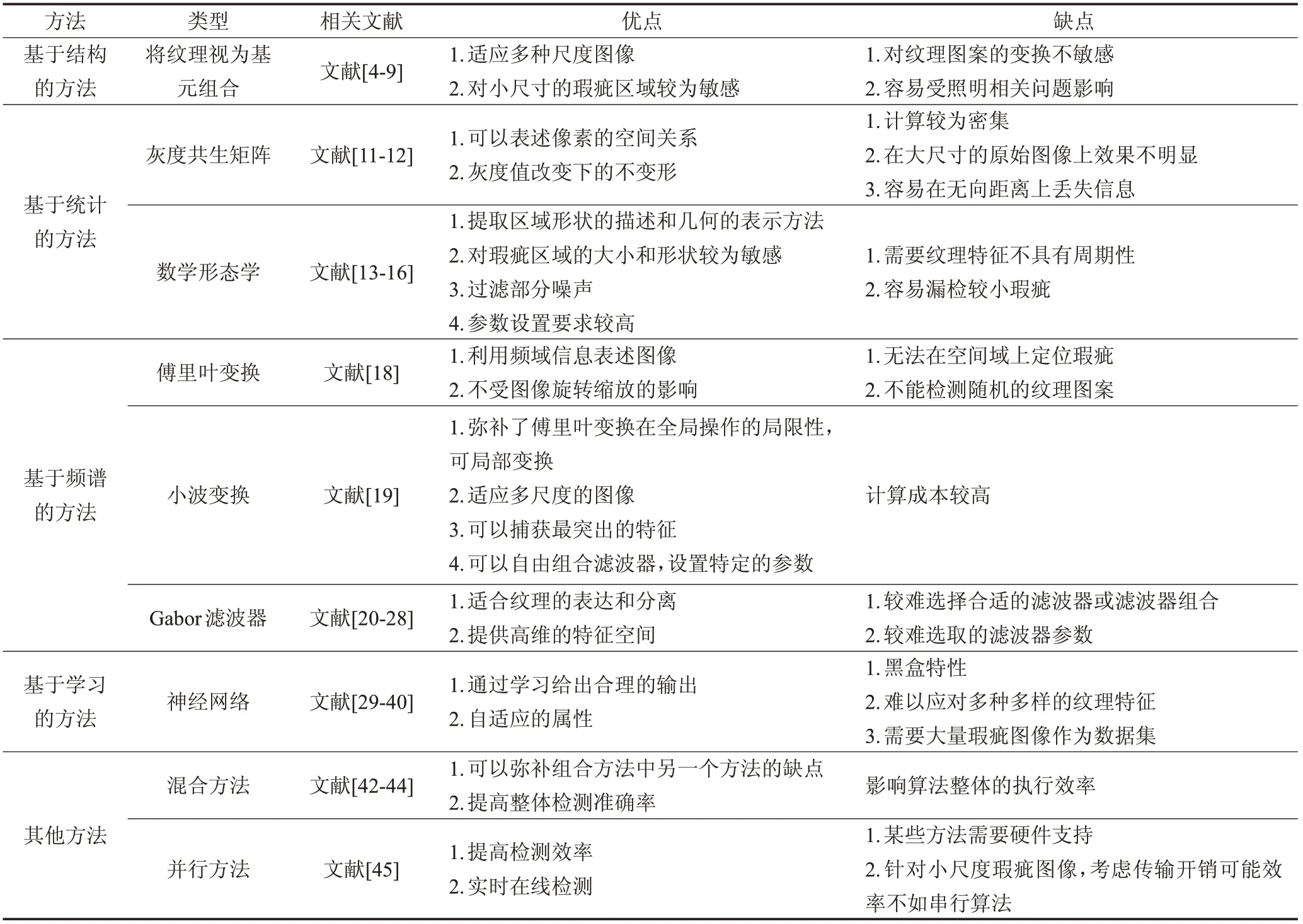
表6 织物瑕疵检测方法优缺点

大多数已发布的织物检测方法只能用于某些壁纸组，最典型的就是p1组，但在其他壁纸组上相关的实验较少。未来需要提出一种尽可能适用于多个壁纸组的瑕疵检测方法。还应在大型样本数据库上广泛评估该方法。

（2）覆盖瑕疵类型更全的织物瑕疵数据库。上一点也说到，大多数的算法只针对研究者手中的瑕疵数据库，而这些数据库在数量上和质量上存在一定差异。希望以后能有一个覆盖17个壁纸组的织物瑕疵数据库以及评价指标用来评估所提出方法的通用性以及可靠性。

（3）新的织物图像采集技术。结合以上分析来看，织物瑕疵检测的准确率以及效率取决于很多的因素，其中，织物图像的采集结果会影响织物检测的准确率与效率。例如使用特定的单色光照射，紫外线照射，红外线照射，以及采集热成像之后的图像等都有可能会对织物瑕疵检测效率带来积极的影响。

（4）多种检测方法的组合。使用混合方法的织物瑕疵检测可以获得更高的检测效率。针对不同方法的优缺点可以适当使用能弥补该方法缺点的方法来提高整体的检测效率。

（5）使用并行方法来提高织物瑕疵的实时检测效率。现阶段，目标识别的研究方向不再局限于提高准确率，识别效率的提高同样重要。目前，织物瑕疵检测大多使用串行算法来检测瑕疵，目前流行的CUDA可以为织物瑕疵的实时在线检测提供更好的支撑。