聚类混合型数据的密度峰值改进算法
谭 阳,唐德权,曹守富
1.湖南师范大学 数学与统计学院,长沙410081
2.湖南广播电视大学 网络技术系,长沙410004
3.湖南警察学院 信息技术系,长沙410138
1 引言
聚类作为一种重要的数据分析方法已在许多领域得到广泛应用,作为机器自动识别数据内在结构的研究重点[1],聚类的任务是在没有训练样本的情况下,仅利用样本间的相似性寻找样本集针对某个评判准则的最佳类别划分。随着聚类分析在金融、商业和社会学等领域的应用不断深入,使用的混合型数据进行聚类的算法研究备受关注[2]。在混合型数据中,大多数样本的特征表述采用连续型、分类型和顺序型属性[3],由于三种属性类型具有不同的特点,为混合型数据建立一个合理可行的相似性度量一直是国内、外学者们研究的重点[4-5]。
样本属性的编码以及相似性度量是设计针对混合数据的聚类算法的关键。对性质简单的数据聚类多使用源于K-means算法[6]的编码方式,即每个样本只对K个聚类中心进行编码,然后利用数据样本与聚类中心的相似程度进行簇类划分。因此,相似性度量对这类算法的性能具有重要影响。其中,最普遍的相似性度量为欧氏距离法,虽然以欧氏距离作为相似性度量,较经典的梯度下降的方式在全局最优化的性能上有了较大的提高,但是面对混合型这种在多重维度空间分布的数据,效果却不够理想。Huang等在文献[7]中提出了K-Prototype算法,该算法将样本属性划分为数值型和分类型,使不同的数据对象集合分别对应不同的属性维度集合,即将样本属性划分到不同的子空间,再进行欧氏距离的相似性度量,最后再将两者结合起来度量样本个体间的差异。虽然K-Prototype算法能够处理混合型数据集,但仍然存在与K-means算法相同的缺陷:算法对空间中分布为球体或超球体的数据具有较好的性能,而对空间分布复杂的数据则效果较差。这是基于欧氏距离相似性度量的缺陷所导致的必然结果[8]。
为此,国内外的研究者提出了各种改进方法。Maulik等在文献[9]中先通过遗传算法来确定特征空间中的聚类中心,再以这些中心来优化聚类的相似性度量,并以此提出了遗传聚类算法(Genetic Algorithmbased Clustering technique,GAC)。在文献[10]中Mei等针对数据的相似性分析提出了一种模糊聚类算法(The Proposed Fuzzy Cluster,PFC),该算法在聚类中采用权重机制对每个集群赋予权重值,以区分样本的基础数据结构,为后续的聚类过程提供先验知识。文献[11]中,Chatzis在模糊C均值聚类算法的基础上提出了(Fuzzy C-Means-type,FCM-type)算法,采用全概率相异性函数来处理混合属性数据,通过交叉熵使得模糊目标函数正则化,使其可以同时对混合型数据的数值型属性和分类型属性实施分类,实现了提高聚类精度的目的。赵兴旺等在文献[12]中利用类内和类间信息熵来度量各个属性在聚类过程中的作用,提出了基于信息熵的数据属性加权聚类算法,通过赋予不同的属性不同的权重,使得数据样本可以在较为统一的框架下更为客观地度量数据样本及样本与簇原型之间的相似性。目前,处理混合型数据的方式是将样本属性划分到不同的子空间中分别进行度量后再进行整合评价。但此举将分割样本属性的统一,导致属性评价的非一致;从而产生对样本的识别偏差,影响类簇划分的效果。
近年来,利用数据样本的最小邻域来发现任意形状的密度聚类方法受到了广泛的关注[13-14],这种基于密度聚类的方法具备在存有噪声的大数据集中找到任意形状的特性。Rodriguez等[15]提出了一种密度峰值聚类算法(Density Peaks Clustering algorithm,DPC),该算法通过利用决策图(decision graph)来快速选择聚类中心,不仅运行高效且具有能发现任意形状数据集并自动确定簇数的优点,但DPC算法的缺陷是其使用范围仅限于数值型数据集。为此,本文提出一种能够有效处理混合型数据的密度峰值聚类算法——海明度量的密度峰值聚类算法(Density Peak Clustering algorithm for Hamming metrics,DPCH),算法以二进制方式对样本的属性进行编码,再对属性编码施行海明差异评价,并依据不同属性的性质赋予不同的属性权重,以此度量样本间的相似程度。通过在统一的框架内对混合型数据实施相似性度量,可有效避免对样本属性的切割,算法以海明度量计算样本个体间密度和局部密度,以决策图的方式来发现混合数据集的聚类中心。仿真实验结果表明,算法可对混合型数据集进行有效的类簇识别。
2 基于海明密度峰值的混合数据聚类算法
混合型数据由于其度量函数的复杂性,使得早期的聚类算法难以对其进行有效的聚类。近年来,对混合型数据聚类的研究重点在如何度量数据样本之间的相似性;虽然通过类型划分属性的方式可以对样本属性的相似性进行分别度量,但始终不能满足多种数据类型在同一体系内进行评价和处理的要求。
2.1 规一化数据集
若存在一数据集,其中包含n个样本,数据集可表示为X={ x1,x2,…,xn},数据集中样本的属性数为d,分别为{ A1,A2,…,Ad}。以二进制对样本的全部属性进行编码,若样本的第R( R =1,2,…,d)个属性AR的二进制编码长度为LR,则属性AR的编码空间为BR={0,1}LR,且属性AR(AR⊆BR)为一有限点的集合。那么,对于第i(i=1,2,…,n)个样本xi的第R个属性表示为ARi,其编码长度为LRi;样本xi的另一属性J(R≠J)的二进制编码长度为LJi。就样本xi而言,依据其自身属性的性质来确定该属性的二进制编码长度,不同属性间的编码长度无需一致。但数据集中样本的同一属性AR的编码长度LRi,(i=1,2,…,n)一致,如图1所示(*表示属性编码长度)。
2.2 样本属性的海明距离
若样本xi(i=1,2,…,n)的第R个属性为AR,则样本xi的属性AR表示为xiR,xiR=r1,r2,…,rl,…,rLR称
rl(l=1,2,…,LR),rl∈{0,1}

图1 样本属性2维表
为属性编码元。对于任意两个样本xi与xj(xi,xj∈X)在任一属性AR下的海明距离度量hR(xi,xj)为:
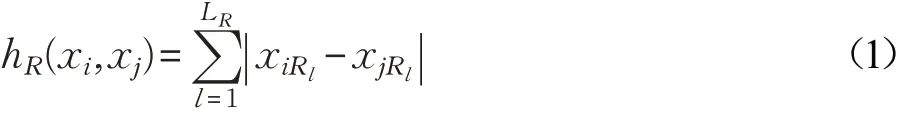
其中,xiRl表示样本xi在属性AR下的第l个属性编码元。由式(1)可知0≤hR(xi,xj)≤LR,hR(xi,xj)=hR(xj,xi)即hR是对称的,且只有在xiR=xjR时hR(xi,xj)=0。由式(1)取得样本属性的海明距离后,则任意两个样本之间海明距离为:
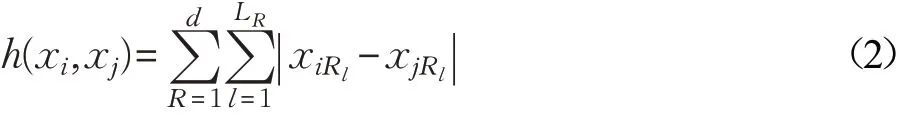
由式(1)可知,属性AR的编码长度LR对应该属性海明距离值hR的取值范围。显然,不同属性的取值范围并非一致,这必将导致样本整体评价的非一致性。另外,在实际聚类操作中经常需要凸显样本中一些重要的属性[12],但这些属性并不一定具有较长的二进制编码,因此,需要对不同属性赋予不同的系数以调整属性的权重。
2.3 属性权重
在实际数据集中样本的部分属性会对聚类结果产生很大影响。因此,通常也将属性的意义看作数据集相对于这个属性的不均匀程度[16]。若某一属性包含信息量较大,就该属性而言,数据集中样本的不均匀程度越高,该属性的重要性也就越大。若样本xi的第R个属性AR有2L个取值,分别为{aR1,aR2,…,aR2L}。在一般情况下,对于属性AR的熵值由式(3)进行计算:
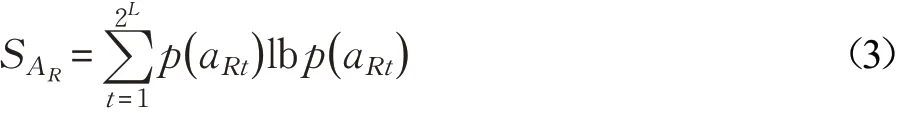
此时,将属性AR看作一个离散随机型变量,其概率分布如式(4)所示:

其中,P( AR=aRt)表示在整个数据集中属性AR的属性值为aRt的样本所占比例,其计算公式如式(5)所示:
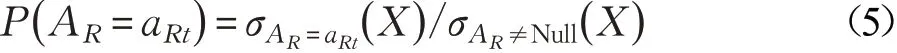
在完成全部属性{A1,A2,…,Ad}的评价后,属性AR的权重值αR由式(6)计算:

2.4 样本间的海明度量
混合型数据样本包含数值和分类两种属性,就分类属性而言其取值范围通常为一有限集中的离散值。传统方法是将其视作无序型数值,并进行简单的0-1匹配,忽略了分类属性值之间的关联性。这也是导致欧式距离和简单匹配方法对混合型数据划分效果不理想的主要原因。为此,通过忽略混合型数据属性的分类,将所有样本在统一编码条件下进行编码和评价,则可消除数值型和分类型属性之间的编码差异及评价体系差异。
设数据集X={x1,x2,…,xn}是一个由d个属性所描述的数据集,若在聚类过程中被指定划分为K个簇类,即C={C1,C2,…,CK},且1,2,…,K;i≠j)。在聚类混合型数据的结果中,簇类的熵值由类内样本属性的熵所确定,某个属性的不确定性程度越小则熵越小,表明该属性的信息量越大。同理,某一簇类在不同属性AR,(R=1,2,…,d)下数据分布的不确定程度越小,则该属性在该簇类中的不确定性越小,在聚类过程中该属性的作用程度越大。因此,在属性AR下,任意一个簇类CK∈C的类内熵WEC(CK,AR)
可表示为:
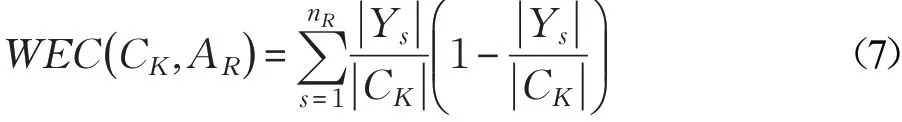
其中,nR表示在属性AR值域的个数, ||Ys表示在属性AR值域中的第s个取值Ys在簇类CK中出现的次数,|CK|表示簇类CK中样本的个数。簇类CK的类内熵表示类内数据分布的不确定程度,类内熵越小表明类内数据的相似程度越高。结合式(7)和式(2)可知,任意一个类CK的类内熵(CK,AR)与类内任意两样本间的海明距离有如下关系:
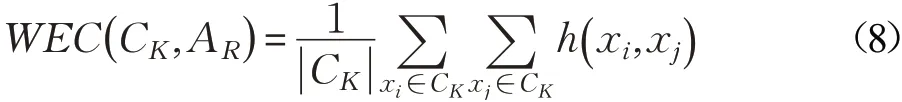
由式(8)可知,类内样本的差异值只取决于样本属性的海明差异,与属性的性质无关。以统一的编码对混合型数据进行海明度量,可消除不同属性表达类型之间度量量纲的差异性,避免了在多维空间中实施距离比较的复杂计算和评价不同属性类型的非一致性问题。
属性编码长度的不统一,会导致对样本整体评价的差异。虽然式(6)针对属性所含的信息量大小,给出了统一的权重值计算方法,免去了不同属性度量之间复杂的参数设置。但是,仍有必要对所有属性海明度量的取值范围进行规整,使其统一到固定的区间之内。对属性AR实行hR(xi,xj)/LR计算,将评价的取值范围规整到[0 ,1]区间内,满足属性评价的一致性要求。数据集X={ x1,x2,…,xn}中任意两个样本xi与xj( i≠j)之间的海明度量H(xi,xj)为:
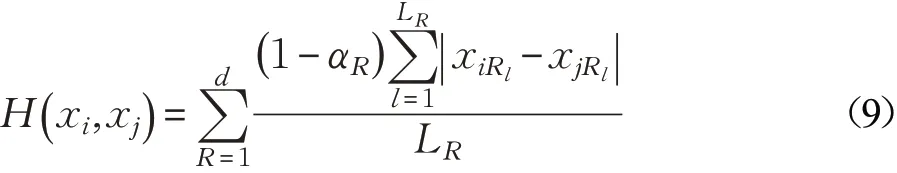
其中,1-αR表示属性AR的加权系数,属性AR的权重值αR越高,样本间的海明度量越低,样本间的相似性越高。混合型数据在统一编码条件下进行编码,以海明差异作为混合型样本的比较,将不同属性间的相似性转换成离散空间中编码的海明差异,能够更加宏观地反映混合数据中个体与簇类之间的差异性。
2.5 数据集的海明密度峰值聚类中心
Rodriguez等[15]提出的DPC算法是利用数据集中样本的密度信息来构建决策图,该算法不仅可以避免孤立样本和噪声对基类的影响,还能有效处理具有不规则形状的聚类和任意形状数据的特性。
2.5.1 构建决策图
数据集X中的样本xi(i=1,2,…,n),ρi表示为样本xi的局部海明密度,即除样本xi自身以外,与xi的海明度量小于Hc的样本个数。

其中:

参数Hc( Hc>0)为截断距离(cutoff distance)。
δi是样本xi到任何比其密度大的其他样本个体间的海明度量的最小值,设的一个降序排列,即满足ρq1≥ρq2≥…≥ρqn,则:
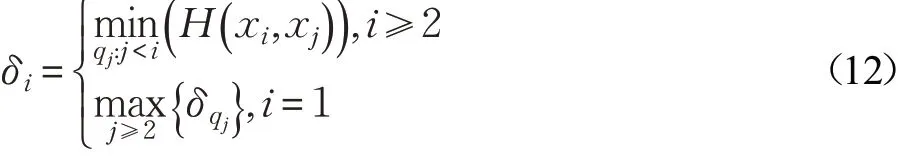
若某样本xi的ρi和δi的取值均较大,则该样本具有个体的局部海明密度较周围样本更大,且样本的簇中心离比自身密度更大样本的距离较远,即不同簇中心之间的距离相对较远。因此,利用以ρ为横轴δ为纵轴的决策图即可判断样本个体是否可以成为聚类中心。
2.5.2 截断参数的选择
通常DPC算法通过挑选合适的截断参数值,使数据集中所有样本的相邻平均数量处于0.01n~0.04n之间。对不同数据集进行聚类则需要采用不同的截断参数,通常截断参数的指定值是以人为经验来确定;这将导致难以确定对未知数据集聚类的截断参数[17]。为了解决这一问题,这里使用从数据集中自动提取截断参数的方法。文献[18]中提出了一种基于引力衍生的数据场,该数据场原理与空间中物体对其他物体施加引力并同时被其他物体吸引类似,即数据场内的数据都能独立地向外辐射能量并接受其他数据所辐射出的能量。基于此,本文采用数据空间中描述样本间共同的交互作用(编码的相似性)来计算截断参数。样本的势函数为:
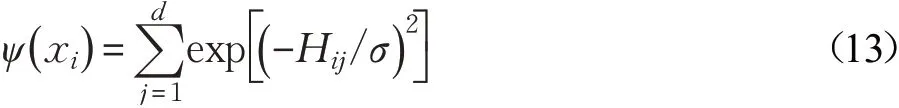
其中,Hij表示样本xi与其他样本xj之间的海明差异值,σ为场影响因子。
当数据场中的势函数和密度公式都取截断核函数时,样本xi在数据场中的势ψ( )xi和样本的熵等价,样本的势越大,熵值越高。则数据集的总熵值S为:
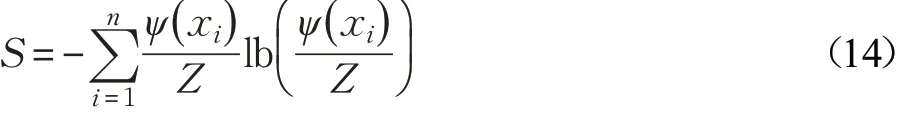
在数据域中样本的编码差异较为均匀,则表明数据集分布的不确定性较大,数据集的总体熵值较大。若样本的编码差异较大,则表明数据集分布的不确定性较小,数据集的总熵值较小,此时数据集更易于聚类划分。因此,通过计算使数据集总熵S达到最小的影响因子σ,即为对混合型数据集进行海明密度峰值聚类的最优截断参数Hc。
2.6 算法流程
若对数据集X指定K个簇类的聚类,则基于海明密度峰值的混合数据聚类算法(DPCH)的算法流程如下:
步骤1初始化数据集,对数据集X中的样本以二进制做规一化处理并计算所有属性的权重值α,根据式(7)计算样本间的海明度量H( xi,xj)。
步骤2用式(14)计算截断参数Hc,并分别用式(10)和式(12)计算每个数据样本xi的局部海明密度ρi和高密度距离δi。
步骤3构造以ρ为横轴,δ为纵轴的决策图。并选择前K个ρ×δ值较大的样本作为聚类中心点。
步骤4计算数据集中其他样本与K个聚类中心点的海明度量,并将与其海明度量最小的聚类中心划归一类。
步骤5依据ρ值的降序过滤噪声及离群样本,其密度不超过边界。
步骤6完成聚类并输出簇类标签。
由样本间海明密度信息所构造的DPCH算法的优势主要体现为:在统一的环境下对混合型数据集样本属性进行编码,消除了数值型和分类型属性之间编码及评价体系的差异;能够自适应混合型数据形状的分布,并且能自动确定簇的个数。通过数据场势函数自动计算的截断参数,避免了人为经验造成的差异,提升了聚类的准确率。
3 实验与结果分析
为分析DPCH的性能,本文选取K-Prototypes、GAC、FMC-type三种聚类算法进行性能比较。采用的测试数据集包括UCI库[19]中的混合型数据集和20-News groups库[20]中的文本数据集。并参照原文献中的数据参数,使用Python重写了所有对比算法。实验平台为:Core i5 3.3 GHz的CPU和8 GB的RAM。采用聚类准确率以及其稳定性(标准差)来共同评价,聚类的正确率(Clustering Accuracy,CA)为:

其中,n为样本总数,ai表示第i类中被正确归类的样本数。聚类正确率为聚类样本个数与数据集样本总数的比值。其结果为区间[ ]0,1内的正数,值越大表明聚类效果越好。
3.1 在UCI数据集上的比较
选取UCI数据库中5个具有代表性的混合型数据集(如表1所示)。
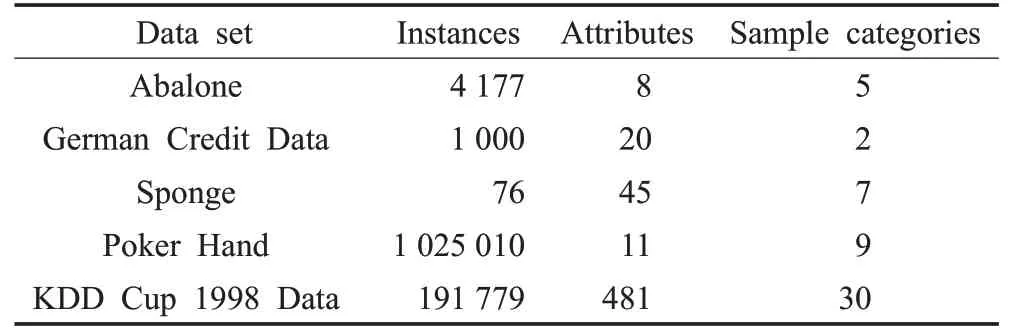
表1 实验中所使用的UCI数据集
4种对比算法分别对UCI中的5个混合型数据集独立运行50次,并对这5种算法在求解不同聚类问题时得到的聚类正确率平均值和标准差进行了比较(如表2所示)。
由表1可知,Abalone数据集样本数量较多且样本属性较少,DPCH容易从高密度区域中发现聚类中心,取得了与FMC-type算法接近的准确性。German Credit Data数据集是经典的混合型数据集,对其研究较为充分,因该数据集的簇类数较少,聚类中心易于确定,各对比算法均取得了较好的准确性。Sponge数据集的样本数量较少且样本属性相对较多,从表2中的结果来看,虽然DPCH的准确率较其他算法占优但仍不够理想。经分析,样本属性数量的增加会导致在二进制编码环境下样本个体的属性编码长度增加,从而在客观上增加样本的取值空间,导致各样本之间的海明差异量相对降低。同时,由于数据集中样本数量较少,DPCH对数据集的局部密度区分受限,影响算法对高密度中心的识别。Poker Hand数据集样本数量巨大,在测试中可以看出各对比算法的准确率均取得了较好的结果,这也表明样本数量的增加能够使DPCH更好地识别高密度中心。KDD Cup 1998 Data为样本数和样本属性数均巨大的数据集,DPCH相较其他对比算法准确率更具优势,这是因为其他对比算法是将数值型属性和分类型属性分别进行计算,并采用降低非占优属性对数据对象整体相似性的影响来进行相似性计算,因而会不断累积对不同属性类型的评价偏差。而DPCH能够针对混合型数据的特点,在统一评价体系内均衡的评价每一维属性,避免了对样本属性调整所带来的偏差,以此获得了较好的聚类质量。虽然表2中5个UCI数据集的4种对比算法均没有取得完全正确的聚类结果;但DPCH在聚类正确率这一指标上优于其他3种对比算法,表明DPCH能够有效聚类混合型数据且具有占优的性能。
聚类的准确率需要在数据类别已知的情况下才能计算,但实际情况中数据集所包含的类别通常是未知的,因此需要通过聚类后的类内距离和类间距离来衡量算法聚类的性能[18]。类内距离(Average distance Within class,AW)反映的是聚类后同一类别中数据关联的紧密程度,距离越小说明同类别数据的关联度越高。
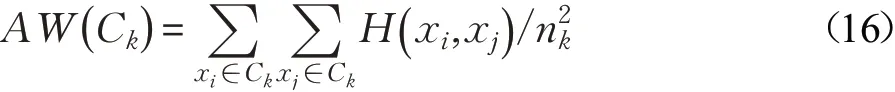
其中,Ck表示第k个类,nk表示第k个类内的样本数。
类间距离(Average Distance Between classes,AB)反映的是聚类后不同类别数据之间的分离程度,距离越大说明数据类别的分离度越高。
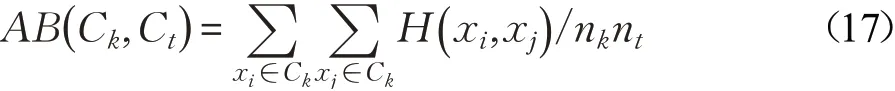
但AW值在不同数据集上的变化不一定表明聚类方法性能的改变,也可能是由数据样本本身的平均类内距离变化所致,因此文献[21]中提出一种综合平均类内距离及平均类间距离的聚类判别指数(Clustering Discriminant Index,CDI)为:
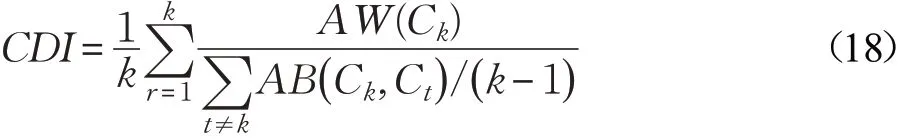
CDI的值由内类距离与类间距离的平均比率所决定,因此CDI值越小说明聚类算法对于样本的基础数据结构具有更好的识别。图2中为4种对比算法在5个UCI数据集上的CDI均值。图中可以看出,DPCH表现出在CDI值上的良好性能。
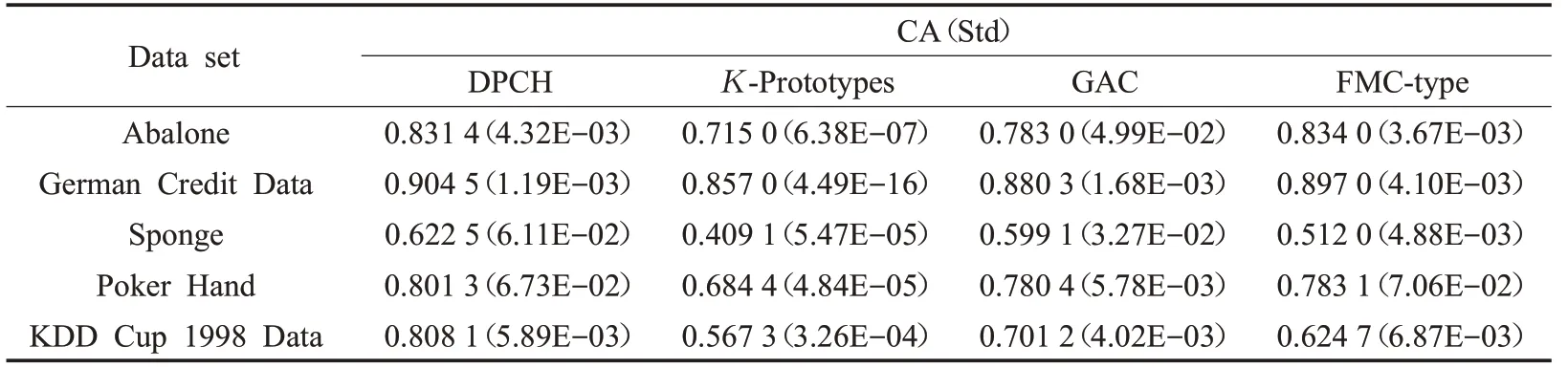
表2 4种算法在UCI数据集上的性能比较
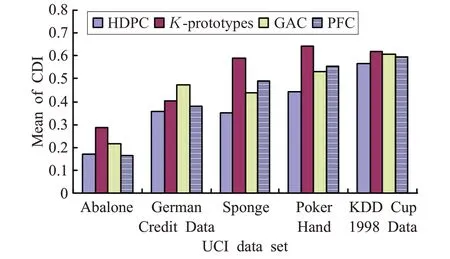
图2 4种对比算法CDI值的比较
3.2 对文本据集的测试情况
为进一步测试DPCH在文本型混合数据上的性能,本文选择采用真实文本数据(未做清洗)做为测试对象。数据来源于20-News groups库中所提供的数据集。该数据集包含了从20种新闻主题中抽取的20 000篇不同内容的消息,平均每个主题的内容为1 000篇新闻。当样本属性类别没有预先进行严格区分时,混合型数据集中不同的样本属性会对聚类结果产生较大影响。本文的测试中选取了20-News groups语料库中3组不同主题的新闻数据集,为了更好地测试聚类算法的性能,每组数据所选取的内容差异跨度较大。表3中数据集A(4)包含了从sci.med等4个主题获取的3 795篇新闻;数据集B(4)中包含了从comp.graphics等另外4个主题获取的3 499篇新闻;数据集C(6)中的5 328篇新闻来源于6个主题,其中包含了其他数据集中已采用过的数据,因此,数据集C(6)较其他两个数据集而言增加了更多的相似内容和重叠的语义信息,在数据信息一致性更高的情况下,会导致聚类难度的增加。
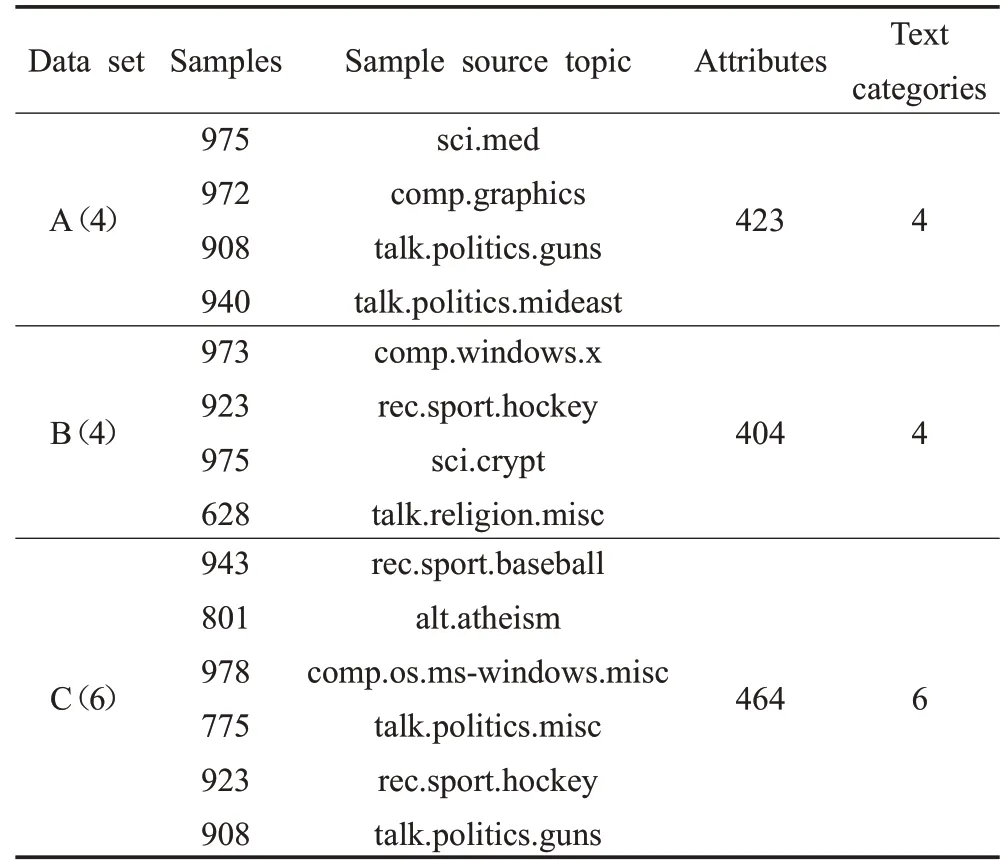
表3 实验中所使用的文本数据集
表4~表6分别给出了4种对比算法在真实文本数据集上的情况,其中包括准确度(CA)和聚类判别指数(CDI)的平均值及标准差。
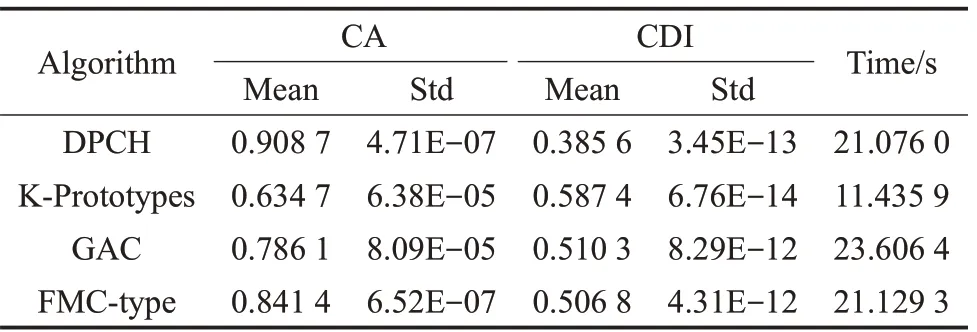
表4 在数据集A(4)上的聚类结果
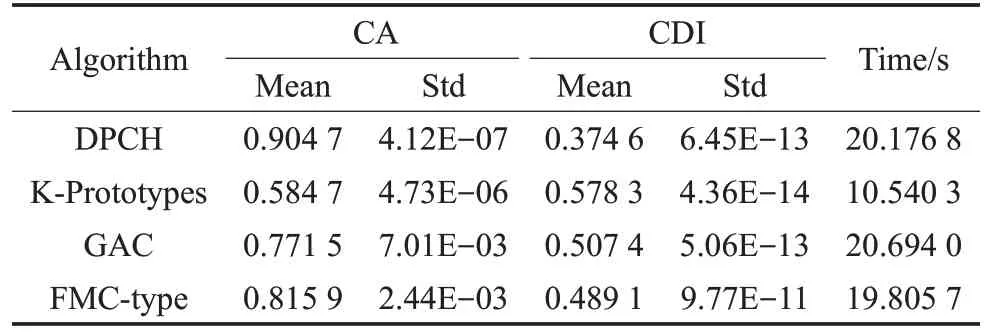
表5 在数据集B(4)上的聚类结果
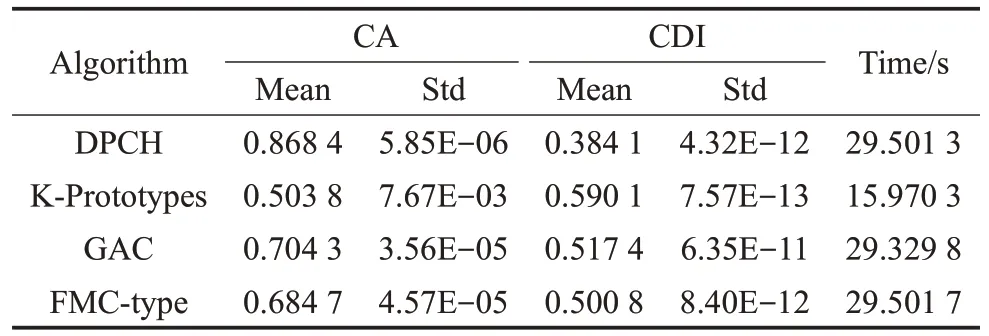
表6 在数据集C(6)上的聚类结果
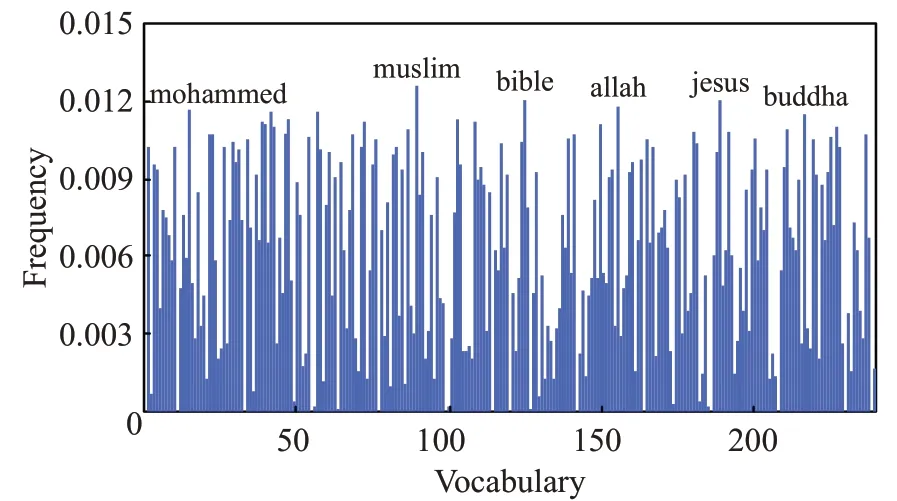
图3 DPCH在数据alt.atheism上的聚类结果
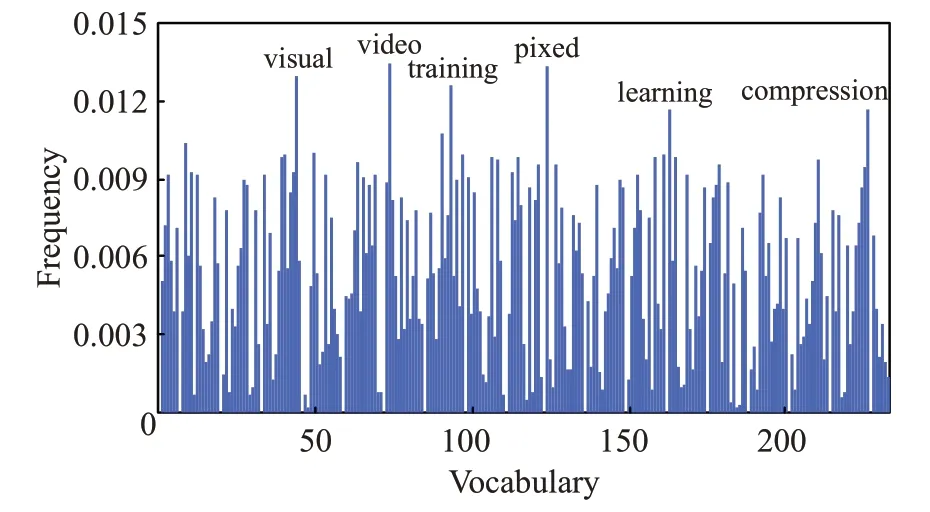
图4 DPCH在数据comp.graphics上的聚类结果
文本型混合数据集属于分类型属性占优的数据,且对词汇和语义的分析不能简单地通过数值比较或空间距离的方式来度量差异。表4~表6的结果表明,DPCH能够在文本型混合数据集上取得良好的聚类结果,除计算时间外,在聚类的准确率和聚类判别指数上均明显优于其他对比算法。在图3、图4中,进一步给出了DPCH算法在对文本型混合数据集聚类时,针对词汇样本频度特征的提取情况。在数据集“alt.atheism”及“comp.graphics”中提取了如:islam、muslim、video和pixel等高特征频度词汇。由此可见,基于海明度量的聚类算法不但可以有效聚类文本型混合数据,也可对数据集中具有较高特征频度的样本进行分辨,为理解数据结构组成及涵义提供支持。
4 结束语
本文提供了一种能够处理混合型数据的聚类算法。该方法通过二进制的方式对样本属性编码,数据集进行规一化处理。并在此基础上采用海明度量的方式来评价样本间相似度,通过构造统一的评价体系对混合型数据实施相似性度量,避免了对样本属性的切割。在聚类过程中受引力衍生的数据场的启发,通过计算数据样本属性的熵值,从数据集中自动提取截断参数的方法实施密度峰值的聚类。UCI数据集和文本型混合数据集上的对比测试结果表明,DPCH算法可更为准确地对混合型数据集进行类簇识别。

