突发事件下人群恐慌情绪感染模型与干预方法

吴新杰，王维莉，胡志华

上海海事大学 物流科学与工程研究院，上海201306

1 引言

随着城市交通系统的发展，地铁因准时、经济环保、高承载量等特点而成为城市交通系统的重要组成部分。近年来，地铁人员的高密度、高流动率已经成为许多地铁车站的运营常态。突发事件时人群因恐慌情绪的传播而导致的混乱极易引发踩踏等严重事故。例如：2015年4月20日上午8点30分，深圳黄贝岭地铁站站台上一名乘客晕倒，部分乘客见状误以为发生恐怖袭击，慌乱逃开。随着事发点人群的慌乱逃窜引起附近周围人群的恐慌而盲目跟随，导致小范围的拥挤和踩踏，造成12名乘客受伤入院。如何提高地铁等人群密集场所的突发事件管控能力已经成为城市应急管理的重要问题。

为合理高效地进行人群管控，需了解突发事件下集聚人群复杂的疏散行为。因此学者们从早期宏观的人群疏散行为研究中开始逐渐深入关注不同个体的疏散行为及其相互作用。如Blue等基于规则提出的元胞自动机模型[1-2]和Helbing基于力学规律提出的社会力模型[3]，反映了个体在紧急疏散中的交互作用，也模拟再现宏观人群疏散中的自组织行为。后有学者考虑行人的行为特征[4-6]，对以上代表性模型进行改进。如从心理学角度出发结合疏散人员的个性特征[6]，分析群体中情绪感染[7-10]等心理特征对个体决策行为的影响等，如基于评价理论的OCC情感模型、考虑个体个性因素的OCEAN模型皆曾引入到人群行为仿真中以分析情绪对个体认知与决策的影响。与传统的概率阈值型的基于流行病学原理的SIR情绪感染模型相比，基于OCC情绪感染模型能通过对外界认知进行定量计算个体的情感值，而基于OCEAN人格的情绪感染模型考虑到个体的差异性以及双向的交互。更重要的是SIR模型无法模拟单个恐慌源的情绪感染场景，而往往突发事件多数是由单个恐慌源引起的。针对突发事件时密集人群的管控问题，许多学者根据已发生事故的原因和视频分析等提出低成本高收益的预警机制[11-13]，如陈亮在大型活动公共安全风险防治中提出密集人群管理的结构化模型与原则；也有通过分析人群密度、人群状态、人群构成后提出人群预测、人流引导、预警系统、应急疏散和信息管理进行人群管控的办法；大部分研究是从踩踏事故中探究事故发生源，再构建拥挤踩踏事故智能化预警系统。这些研究缺乏针对疏散过程中的干预措施，以及干预措施对人群管理的影响机制分析。因此，本文以地铁站突发事件为背景，针对恐慌人群的情绪感染进行干预，基于社会力模型，模拟不同干预条件下人群疏散的行为演化规律。

2 情绪感染

2.1 个性与情绪感染

由于不同人格的个体具有不同的情绪感染能力，个体情绪的变化规律与个性特征之间存在着密切的关系。例如，具有较高责任感，更敏感的情绪变化和更具外向性的个体更容易出现情绪变化。目前对人格建模最主要的模型是Costa和McCrae提出的OCEAN模型。本文将人格OCEAN模型引入到传染病SIR模型中，建立基于个性化的情绪感染P-SIR模型分析地铁突发事件下对恐慌人群进行干预与无干预[14]时，人群疏散行为的演化规律与疏散动力学特征。

2.2 基于个性化P-SIR的情绪感染模型

在SIR传染病模型的基础上，将个体的情绪状态可分为三类：易感状态（S类），感染状态（I类）和免疫状态（R类），如表1所示。

表1 情绪值分类

P-SIR情绪感染模型中包含的因素，如表2所示。

表2 情绪感染参数

由于每个个体的个性有OCEAN模型的五个维度组成，因此对每个个体定义{ pO,pC,pE,pA,pN}五个因素，取值在[0 ,1]范围内。其中，感染能力与易感能力与个性的关系如表3所示。

表3 OCEAN个性模型

P-SIR情绪感染模型如下所示：

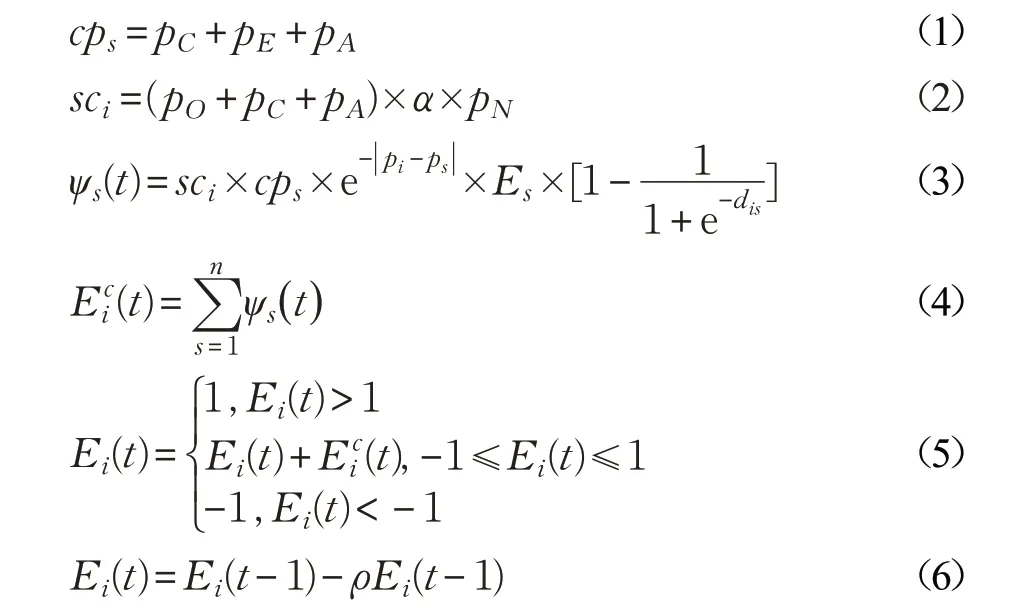
情绪感染模型公式中（1）～（5）表示个体i的自身情绪易感染能力与其周围的恐慌者S的感染能力作用下，个体i的情绪值E增加，并随着个体i与恐慌源S的距离增大，个体间的情绪增加程度变小[6]。式（6）表示在设备干预范围内，在下一个时间步长中，个体i的恐慌情绪值衰减[14]。

在初始恐慌源传播半径rc内，距离最近的敏感个体最先受到感染能力较强的恐慌源的影响触发恐慌情绪，进而作为新的恐慌源对其他个体进行情绪感染。当个体处于恐慌源的传播半径内时，个体的恐慌情绪值Ei(t )超过个体易感阈值T1时，则个体的情绪状态转化为易感状态（S类）；恐慌量持续累加超过个体恐慌阈值T2时，被转化为感染状态（I类），个体的情绪状态的计算如图1所示。当管理员开始干预时，在其干预范围内的个体的情绪状态转化为免疫状态（R类）。当设备干预时，在影响半径内只有一定比例的个体受到影响，情绪出现衰减。计算公式如（6）所示，衰减到低于易感阈值T1时，个体的情绪状态转化为免疫状态（R类）。

ψs(t)为单个感染源对易感个体的影响值，其中恐慌传播源的情绪感染能力cps与其行为表现、情感表达相关的责任感、外向性和亲和性有关。cps是静态值，一旦设定便不随场景改变。个体i对周围恐慌传播源的易感染能力sci是由个体i个性中与情感捕捉、理解力有关的探险性、外向性、亲和性、敏感度的维度决定。α为敏感参数，调整感染速率的参数值。

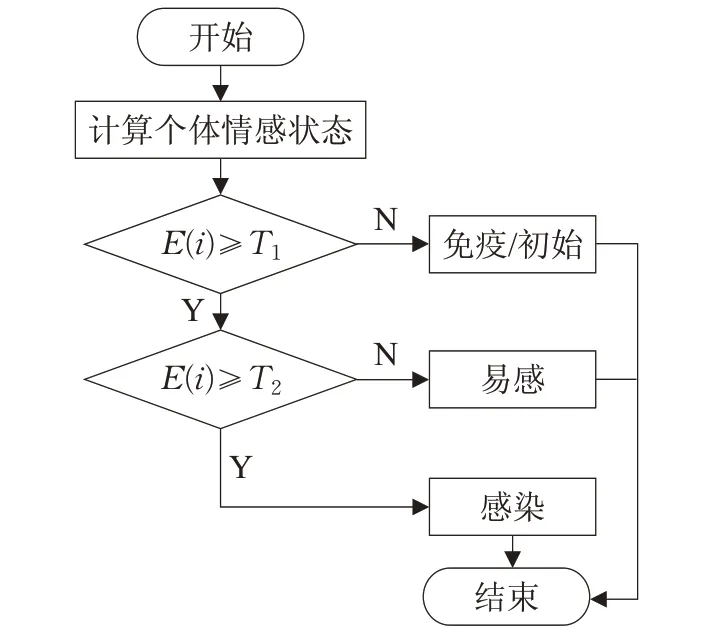
图1 情绪感染流程图

2.3 恐慌人群干预模型

在突发事件时，为了阻止恐慌情绪的传播造成不必要的生命财产损失，需要对恐慌人群进行管理与控制使其不造成更严重的后果，因此本文提出两种恐慌人群干预策略。

（1）管理员干预

管理员对现场人群进行情绪疏导，则能使其附近的恐慌人群的情绪得到平复，恢复冷静状态。假设管理员的作用半径为rc，在其范围内的个体转化为免疫状态（R类），不受其他个体的影响；离开作用半径后重新转化为S类。

（2）设备干预

当突发事件后，现场工作人员使用信息传播方法，如无线电和扬声器，对其影响半径rm内的所有人进行干预，平复人群的恐慌情绪并进行疏导。假设该范围内受影响的个体比例为ω，如公式（7）所示，与恐慌个体的pN人格有关，即保持自身消极情绪状态的持久倾向[15]。当pN≥0.5时，个体倾向于改变恐慌状态，pN＜0.5时，个体将保持恐慌状态。在设备干预范围内倾向于改变恐慌状态的个体情绪开始衰减，衰减因子为ρ。但仍会受到未改变恐慌状态个体的影响，而离开干预范围后情绪将不再衰减。

3 行为驱动下的运动模型

3.1 社会力模型

社会力模型是目前研究微观行人行为最广泛的模型之一，它是基于牛顿第二定律与加速度间的相互关系[3]。式（9）表示人的运动是由目标驱动力、行人间的相互作用力以及行人与墙的相互作用力三个力的合力驱动，三个力分别描述为式（10）～（14）。

社会力模型如下所示：

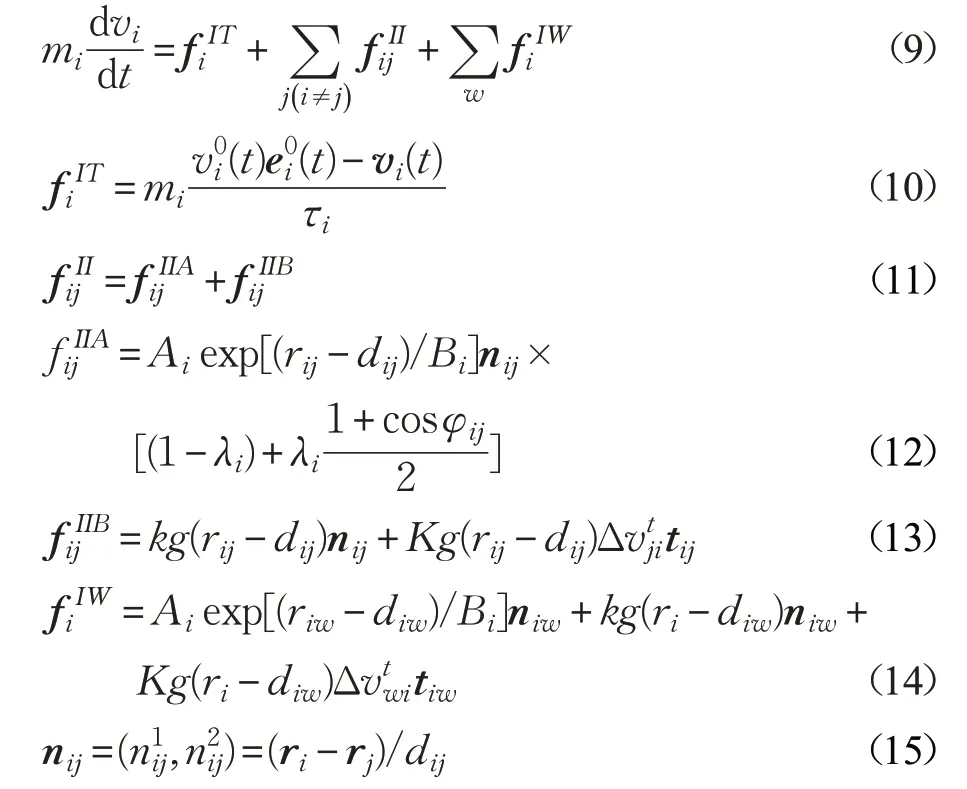
式（9）中，mi指行人的质量，是行人沿着单位矢量的方向的期望速度，τi为行人的从当前时间vi(t)加速到大小的相应时间。表示行人向目标行进的动力。式（11）中是由未接触时的心理排斥力和接触时的物理力组成行人间的相互作用力。其中物理力由身体挤压力以及滑动摩檫力组成。

式（12）中，λi是视觉影响因子，在当前行人前方的行人比后方影响程度大。φij表示行人i的速度方向与行人ij连线之间的夹角，λi表示视野区域里行人的相对位置对行人间相互作用的影响，0≤λi≤1，λ越大，表明视觉对社会力影响越大。心理排斥力主要有行人的心理安全距离和社会性决定。nij表示行人j指向行人i的单位矢量。Ai和Bi是两个常数。当两个体接触时，也即rij≥dij，物理力起到重要作用。式（14）中描述行人与障碍物的相互作用，表达式与类似。其中，diw为行人i与墙之间的距离。

3.2 基于恐慌情绪的社会力模型

恐慌人群的“不适应性”行为在引起冷静或焦虑人群的注意力的同时，也增加了其对恐慌人群的心理排斥力。本文考虑将冷静或焦虑人群所受的周边恐慌人群“恐慌源”产生的“排斥力”引入到社会力模型中[16]，这样，人在疏散时会主动远离恐慌人群。恐慌人群对行人个体产生的排斥力表示如公式（16）所示：

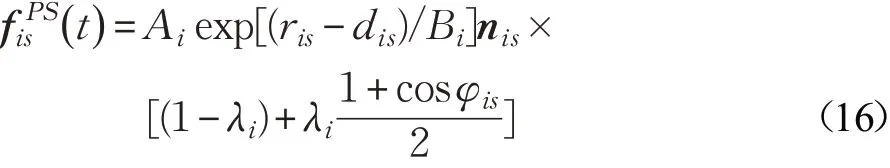
式（16）中，s表示感染源。可以看出，该公式与原始社会力中的排斥力的公式形式相似。提出社会力模型的Helbing等人在模拟恐慌人群的疏散实验时认为个体的恐慌情绪对期望运动速度和期望运动方向有影响，再现了恐慌者选择期望方向时跟随周围人群的“羊群效应”和“快即是慢效应”[3，17]。谢科范将恐慌情绪引入到社会力模型的自驱动力和行人间的相互作用力中模拟恐慌源周围的人群面对突发事件时向远离恐慌源的方向四散逃开的疏散过程，而且发现情绪超过某一阈值时，个体的运动状态呈现离散、随机性移动，与目标方向有一定偏离[14]。考虑到个体在疏散过程中自身驱动力和对恐慌源的心理排斥力都会受到恐慌情绪的影响，因此将恐慌情绪值引入到社会力模型中，整合后如下所示[14]：

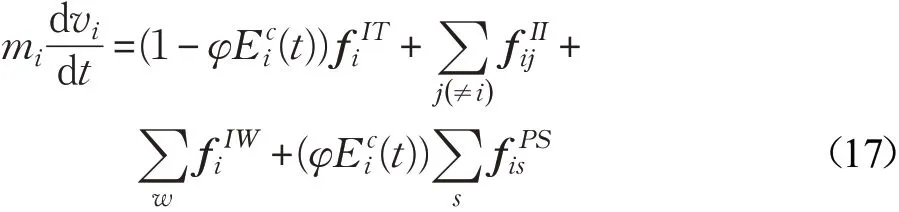
其中，φ=0.2为恐慌情绪系数，Eci(t)为个体从恐慌源感染恐慌情绪值。疏散个体在恐慌情绪的影响下，在与其他恐慌源保持相应的距离的前提下，向着出口方向运动。因此目标驱动力会受到恐慌情绪的影响，且与恐慌情绪系数有关[14]。

3.3 模型参数

本文模型的参数如表4所示，主要基于已有研究[3，17]确定，除此之外，其他参数通过敏感性分析校正后确定。

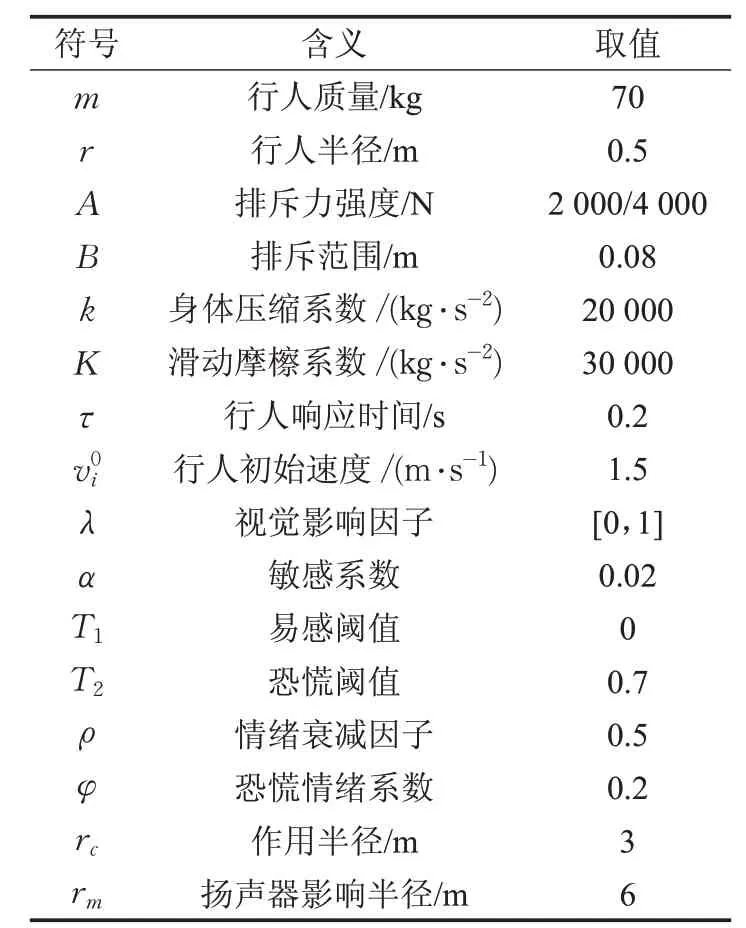
表4 模型参数

4 仿真及结果

4.1 仿真场景

仿真实验设置为一个16 m×8 m的地铁站通道，如图2所示，其中一个楼梯出口设置在中间位置，出口宽度设置为2 m，总人数为N。以随机位置和随机方向分配在该环境中。实验分析疏散过程中恐慌情绪感染效应和干预对疏散时间的影响，对给定的参数，每个场景开展50次的模拟，实验结果取平均值，以降低偶然误差带来的影响。

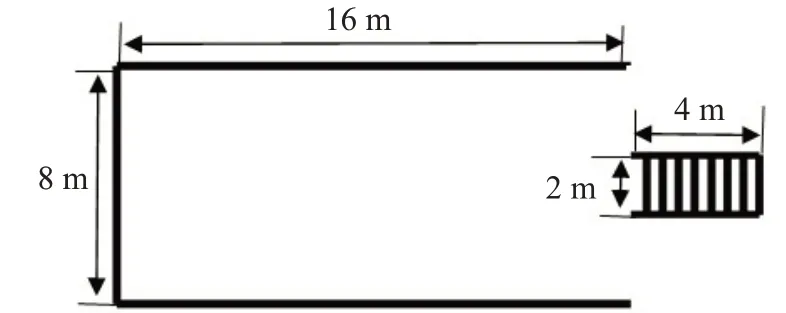
图2 实验环境图

4.2 实验结果分析

4.2.1 模型参数分析

为了研究疏散过程中的干预策略对疏散效率的影响，首先要了解无干预策略下人群在自由疏散过程中初始恐慌源位置对恐慌传播以及疏散效率的影响，以便于提出更佳的干预策略。

（1）敏感系数

根据实际恐慌疏散事件的观察与仿真模拟，在疏散过程中，系统中若不存在恐慌源时，疏散总时间为32 s。如果系统中存在恐慌传播源，恐慌情绪往往传播得非常快，恐慌感染数目达到最大值的时间只需要6～10 s[14]。通过仿真实验发现在P-SIR模型情绪感染模型中，敏感系数α的不同取值，对恐慌源传播时间影响不同。如图3所示，为了更加真实地模拟现实疏散场景，敏感系数取值在[0.02,0.05]范围内，由于在此范围内开始感染时间大致相同，而α=0.02时，恐慌感染数目达到最大值所用时间约为8 s，在实际观察数据6～10 s范围内。

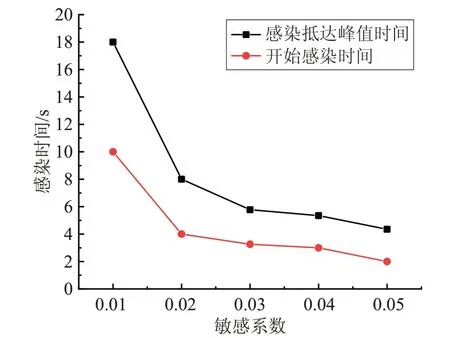
图3 敏感系数与情绪感染的影响

（2）感染能力与易感染能力

为了研究OCEAN模型中个性对疏散效率以及情绪感染速率的影响，分析影响情绪感染的两个关键因素：感染源的感染能力cp和未感染者的易感染能力sc，如图4所示。

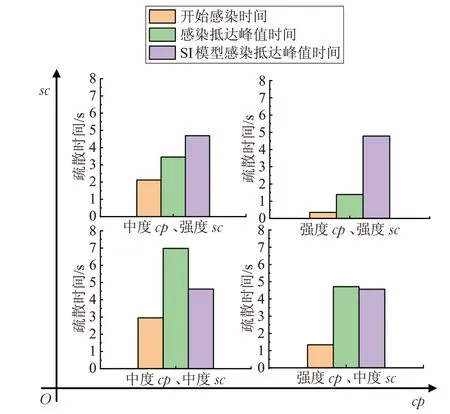
图4 关键因素、SI模型对情绪感染的影响

为了便于观察仿真模拟效果，选取特定个性的人群进行实验。例如，将恐慌源分为中度感染力、强度感染力两类人群，同时将未感染者分为中度易感染力和强度易感染力两类人群，其感染力与易感染力取值见表5。

表5 OCEAN模型关键因素

在疏散过程中，行为表现与面部表情较夸张的恐慌者更易引起恐慌情绪的传播，同时具有好奇心、善于理解他人的具有亲和性的行人更加容易被感染。对初始感染源与未感染者的个性进行分类初始化后，通过对比分析不同特定人群在情绪感染中对开始感染时间和感染抵达峰值时间的影响，以研究感染力与易感染力在OCEAN模型中重要作用。不同特定人群的交互能力对情绪感染的影响如图4中的前两列的条形柱：对于情感捕捉、理解力强的一类未感染者，更容易受恐慌源的影响。对于初始感染源而言，较强的感染力（即表现冲动、性格较外向）对情绪感染影响较大。感染源的感染能力与未感染者的易感染能力相互作用共同影响情绪传播的速率。从图中可知，相对比中度cp、中度sc分类人群，强度cp、中度sc分类人群的情感传染对开始感染时间和感染抵达峰值时间分别缩短了1.51s和2.27s。而对于强度cp、强度sc分类人群的情感传染更加迅速，开始感染时间在0.4s以内，感染抵达峰值时间在1.3s左右。对于这类易恐慌的未感染者和感染力强的初始恐慌源的疏散情况下很难对恐慌人群进行干预，尤其针对青少年，需要做好相应的预警机制以免造成严重后果。

为了分析本文基于个性化的P-SIR情绪感染模型相对于SI情绪感染模型的特点与优势。

将不考虑P-SIR情绪感染模型中的个体的个性因素。假设感染源的感染能力cps=1，未感染者的易感染能力sci=α（此时α=0.02为SI模型中的未感染者的感染率），即未感染者的感染概率相同。将P-SIR模型回归到原始的SI感染模型中，SI模型对情绪感染速率的影响如图4所示第三列紫色条形柱。从图4中可知，SI模型在忽视P-SIR情绪感染模型中个体的个性因素后，情绪感染抵达峰值的时间在4.5s左右，而基于个性化的P-SIR情绪感染模型在不同感染源的感染力与未感染者的易感染能力组合下情绪感染的速率不同。相对比情绪感染SI模型对宏观群体情绪状态的研究，基于个性化的P-SIR情绪感染模型能考虑到个体差异与双向交互作用对不同个体情绪进行定性定量分析，可模拟不同个性人群分布的特定场所，例如少年宫、电影院等。

4.2.2 无干预场景

（1）仿真实验

为观察初始恐慌源位置与出口的距离对恐慌情绪传播以及疏散效率的影响，分析初始恐慌源距离出口不同位置在疏散过程中对感染个体数的影响。

在自由疏散过程中，如图5所示，初始恐慌源对疏散效率的影响与恐慌源离出口的距离有关。当初始恐慌源在出口附近时，对疏散效率的影响与出口附近的人群密度有关。如图6所示，当初始恐慌源周围人群密度低于1.02人/m2时，对恐慌源的行走速度影响极小，可以提前离开疏散系统，因此出口附近的恐慌源周围密度较低时，对疏散系统的威胁很小，整个疏散时间大约等于正常的疏散时间。如表6所示不同人群密度下的疏散速度及步长[18]，当初始恐慌源周围人群密度不断增加时，将导致恐慌源的行走速度降低，不能顺利通过出口，导致恐慌源滞留在出口附近，当人群大量聚集在出口时，情绪感染迅速扩散，在距出口2m范围内恐慌感染个体数最大值达到91人，此时疏散时间最大为39.68s。随着恐慌源与出口之间的距离增加，疏散时间也在不断增加，由于初始恐慌源出现在疏散空间的中间位置时，由于恐慌源的前后人群都受其影响，导致感染人数不断增加，人群的目标驱动力受恐慌情绪的影响，造成了疏散时间延长至38s左右。恐慌源离出口较远时，距离出口较近的人群早一步离开疏散系统，使系统内潜在的易感人群数量不断减少，但如图7所示恐慌感染个体数依然在50人以上，疏散时间保持在36s左右。

（2）典型案例

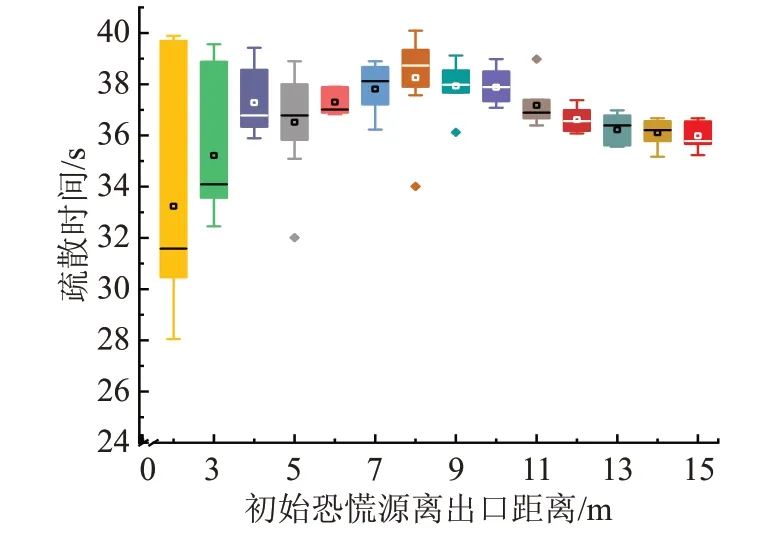
图5 初始恐慌源位置对疏散效率的影响

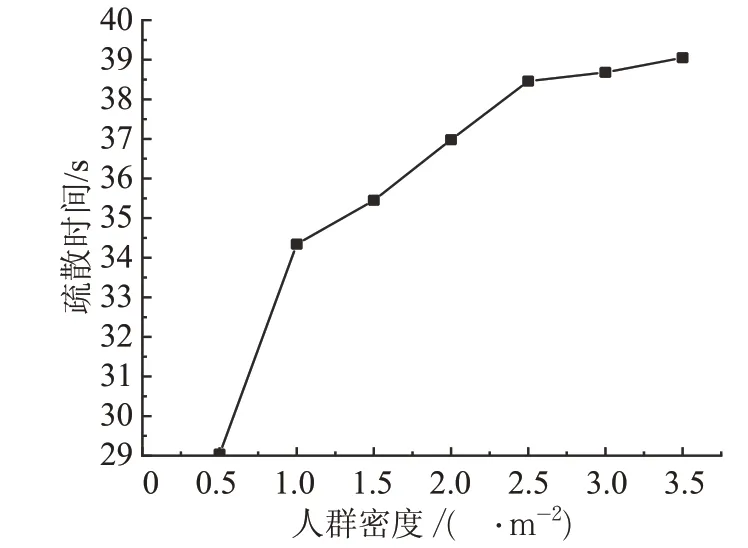
图6 出口位置人群密度对疏散效率的影响

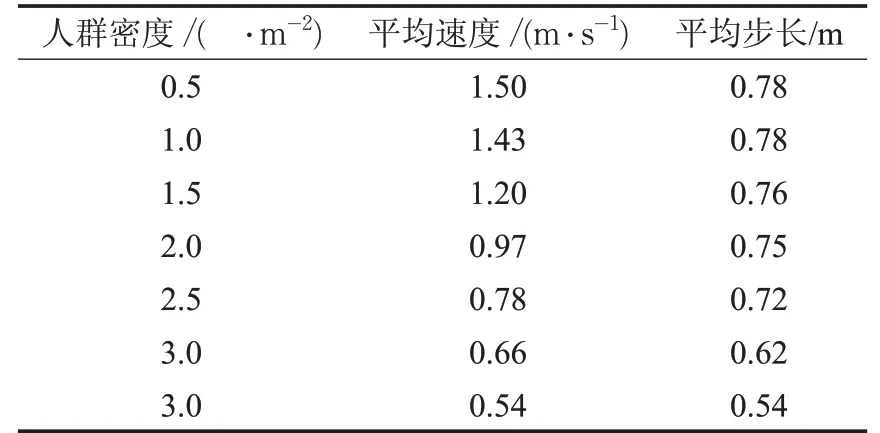
表6 不同人群密度下的疏散速度及步长

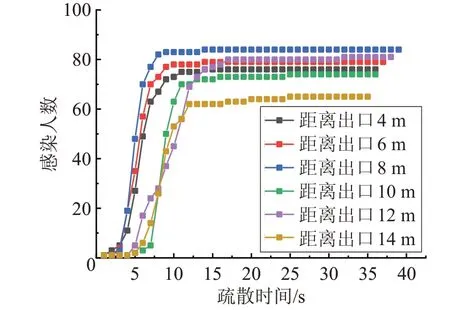
图7 初始恐慌源位置对感染人数的影响

为了有效说明模型对初始恐慌源以及情绪感染模拟的真实性，引入2017年8月13日在深圳地铁发生的恐慌拥挤事故作为案例对比，案例视频截图如图8所示，恐慌源是距出口2 m范围内的一名乘客，由于该名乘客的“异常行为”引起周围人群的注意，导致其周围部分乘客因恐慌情绪产生避让的“恐慌排斥力”和紧急逃离的恐慌行为。随着人群的运动，恐慌情绪继续向周围人群蔓延，产生新的恐慌源。从现实恐慌疏散事件的观察发现：恐慌情绪的传播速度极快，恐慌个体数达到最高值仅需要7 s，随着恐慌人数的增加，秩序更加混乱，人群在恐慌情绪的影响下，向出口方向奔跑。在疏散过程中，出现碰撞跌倒的现象。

图8 深圳地铁事故

4.2.3 对恐慌人群实施干预场景

随着集体行为识别技术以及对突发事件预警的智能系统的发展，可以很快速地对人群计数、视频场景理解、异常行为检测等问题做出反应。相应地对不同个性人群交互作用的研究，更加有助于对异常行为的检测与及时的干预[19]。

为了有效防止人群中的恐慌情绪传播，提高疏散效率，现场管理员以及智能监控系统应实时监控现场的异常行为并及时地进行干预。假设当疏散环境中恐慌个体比例超过阈值z时，相关人员将采用干预策略。根据无干预人群的疏散实验以及实际恐慌疏散实验的观察与仿真分析，当环境中存在恐慌源时，恐慌情绪往往蔓延得极快。如图9所示不同时刻的疏散场景，红色圆圈代表恐慌者，绿色圆圈代表初始无情绪状态的个体，黄色圆圈代表焦虑者。而当管理员要采取行动时，系统状况已经开始迅速恶化，因此应在恐慌开始恶化之前进行干预，即恐慌个体比例在40%时，采取干预，以减少恐慌个体的迅速扩散。

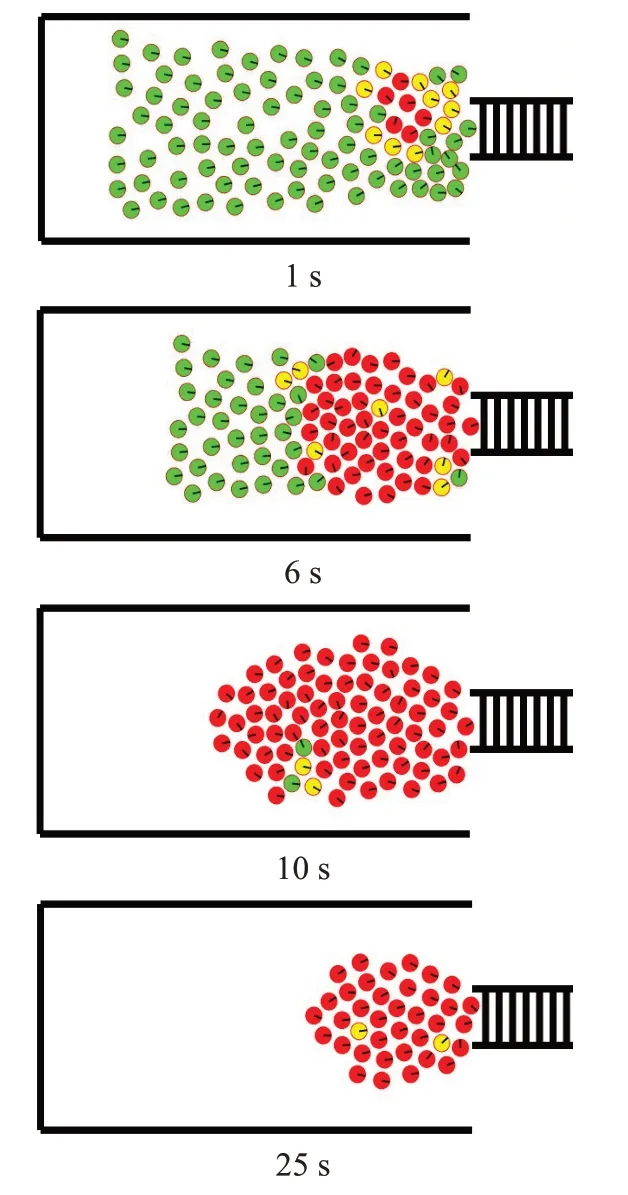
图9 t时刻的疏散场

（1）管理员干预

恐慌疏散的情况下，当恐慌感染个体达到最大值时，如图9所示，在出口附近形成大约11 m的拱形人群，相互拥挤着向出口方向疏散。为了最大限度地提高免疫效率，在距离出口12 m范围内，设置一个管理员，其作用半径rc为3 m，分析管理员的位置对疏散效率的影响，在管理员的干预范围内的个体成为免疫个体，不受其他个体情绪影响，而离开干预范围后，重新恢复易感状态。从图10可看出，当管理员与出口之间距离小于7 m时，恐慌撤离的时间显著减少，这意味着在恐慌个体比例超过阈值z时，恐慌人群主要集中在出口附近7 m范围内，在此干预范围内，疏散时间降低幅度较大。管理员对恐慌个体的干预效果如图11所示，管理员在5 m的出口范围内，恐慌个体的免疫数在70人左右，有效地提高了免疫效率。当管理员与出口之间的距离不断增加时，由于免疫人数不断减少，总疏散时间倾向于无干预情况下的疏散时间。

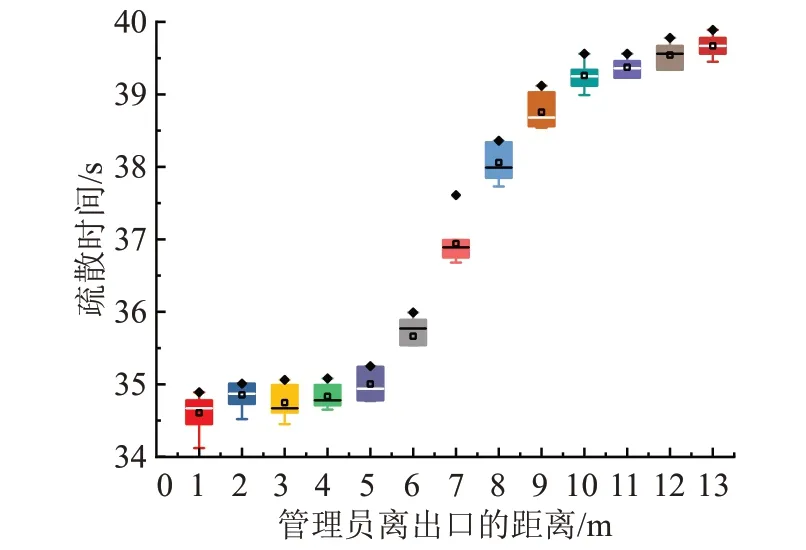
图10 管理员位置对疏散效率的影响

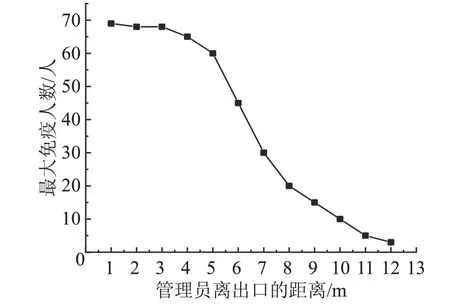
图11 管理员位置对最大免疫人数的影响

（2）设备干预

在紧急情况下，管理者通常很难及时达到最佳的干预位置，因此设备干预是最常见的应急管理方法。由于管理员的干预范围受自身以及环境噪声的影响而受到限制，而扬声器等设备的干预范围较大。扬声器的传播半径为6 m，设置扬声器在离出口6 m距离时，受到设备干预的个体情绪值出现衰减。如图12所示，当倾向改变自身状态的个体数越多，疏散时间越短。倾向改变自身状态的个体数占总人数比例ω为50%～100%时，疏散时间有显著降低。而ω为0%～40%时，对疏散效率影响不大，由于未改变情绪状态的新恐慌源仍对其他人群进行情绪感染。而ω在100%时，疏散效率最快，疏散时间比无设备干预时降低了6.5 s。在疏散过程中，疏散人员的自身因素在应急疏散中占有重要作用。

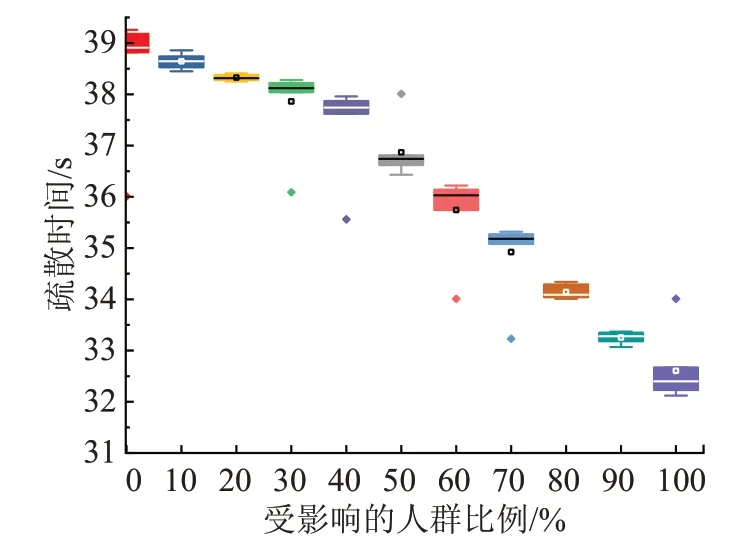
图12 设备干预对疏散效率的影响

管理源干预与设备干预策略结合人格OCEAN模型、基于个性化的P-SIR情绪感染模型、异常行为识别技术的智能监控系统，实现了干预的有效性与实践性。为了更好地进行智能监控以便及时地干预，需要深入研究人群在不同场合的人格分布以及个性与异常行为的关联性。

5 结束语

本文通过建立基于个性化的P-SIR情绪感染模型，模拟地铁站突发事件时的不同情绪状态下的应急疏散，分析在疏散过程中初始恐慌源不同位置对感染人数以及疏散效率的影响。为阻止恐慌情绪的传播，提出管理员干预和设备干预两种干预策略。研究发现：（1）初始恐慌源的位置对情绪感染具有明显的影响作用，在无干预时，初始恐慌源离出口的距离对情绪感染人数影响较大，而当恐慌源在出口附近时，出口附近的人群密度影响恐慌情绪的传播。当人群密度高于1.02人/m2时，出现情绪感染，随着密度的增加，感染人数也逐渐增加，最大值可达91人。（2）存在干预时，管理员的干预位置影响干预效果，当管理源离出口距离为7 m时，疏散时间下降幅度最大，而在离出口3 m范围内时，影响恐慌个体数最多，而且疏散时间最短。（3）设备干预时，干预效果与个体pN人格有关。当倾向改变自身状态的个体数越多，疏散效率越快。本文提出的基于个性化的P-SIR情绪感染模型以及干预策略的分析能为突发事件时的人群管控提供重要的理论支持。另外，相关部门也应开展疏散演练与突发事件发生时的应对演习，以增强对紧急事件的认知与处理能力。