基于粗糙集不确定度的特定类属性约简

吴婉琳， 张贤勇*， 莫智文

（1.四川师范大学 数学科学学院，四川 成都610066； 2.四川师范大学 智能信息与量子信息研究所，四川 成都610066）

粗糙集理论是一种不确定性分析理论，能够有效处理不精确、不完整、不一致数据，最终在决策表中提取决策规则或有用信息［1］.在粗糙集理论中，属性约简是核心内容与研究热点，其主要在保持相同分类能力的前提下进行冗余属性删除，从而达到数据表的优化处理.

决策表具有3层粒度结构［2］，在约简方面涉及到系统决策分类与局部决策类2种主体.传统的属性约简是决策分类约简，主要考虑所有决策类的整体优化.针对实际中存在的局部优化需求，特定类约简应运而生，并改进了决策分类约简的盲点.文献［3］基于正域首先建立特定类约简，文献［4-5］分别从信息度量与三支决策角度推进特定类约简，文献［6-8］分别从邻域粗糙集、三支概率、决策分布的角度深化了特定类约简.粗糙集的不确定性主要存在于边界域，因而基于边界域及其度量的属性约简具有基本的决策表不确定性处理功能.例如，文献［9］得到信息熵约简的边界域条件信息熵表示，文献［10］提出保持边界域划分的知识约简算法，文献［11］给出基于容差关系矩阵的决策表边界域的计算方法，文献［12］提出一种基于边界区域的特征选择算法，文献［13］提出基于粗糙边界域的约简.归纳可见，基于边界域的属性约简主要停留在决策分类约简，而相关的特定类约简罕见相关研究报道.

本文针对特定类属性约简，拟采用粗糙集边界的角度进行初步探讨.为此，主要针对已提出的“决策分类不确定度约简”［13］，对应提出“特定类不确定度约简”，并揭示两者的层次关系与约简关联.具体地，提取特定类的不确定度度量，依托粒化单调性来定义与研究特定类约简及其启发算法，并澄清“特定类不确定度约简”与“特定类正域约简”“决策分类不确定度约简”的关系，最后用决策表实例有效验证相关算法与约简关联.新建的“特定类不确定度约简”的研究框架如图1.

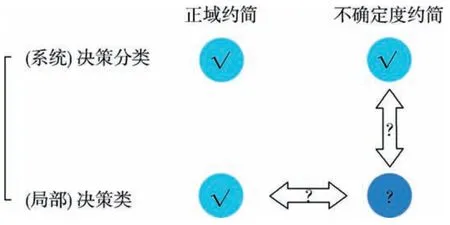
图1 特定类不确定度约简的研究框架Fig.1 The research framework of class-specific attribute reducts based on uncertainty degrees

1 预备知识

首先复习粗糙集约简基本概念，主要涉及决策表的“特定类正域约简”［3］与“决策分类不确定度约简”［13］2种基本模式.

粗糙集属性约简的基本形式背景是决策表

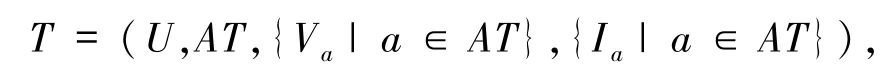
其中，U是非空有限论域，AT是属性集合（其包括不交的条件属性集C与决策属性集D），Va是属性a∈AT的值域，Ia：U→Va是相应信息函数.关于粒化，条件属性子集A⊆C与决策属性集D分别诱导出知识剖分

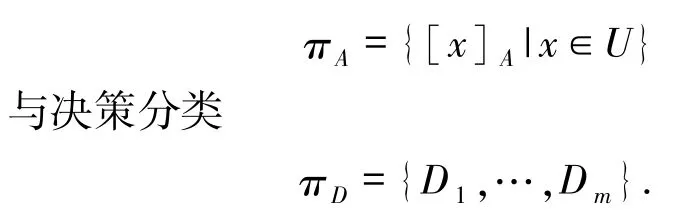
由此决策表具有3层粒度结构［2］，高层（πA，πD）与中层（πA，Dj）分别对应决策分类约简与特定类约简.下面，▯与‖分别表示补集与基数.

定义1［3］关于条件属性子集A⊆C，决策类Dj的正域、负域、边界域为：

定义1提供了粗糙集模型的基本区域与概念不确定性度量.由此，定义2采用决策类正域自然定义了特定类约简.类似地，可以采用决策分类正域定义决策分类约简.下面，基于不确定度来聚焦决策分类约简.

定义3［13］关于条件属性子集A⊆C，决策分类πD的不确定度为

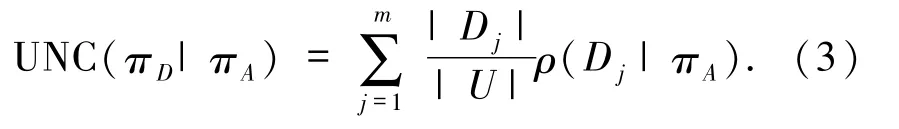
定义4［13］条件属性子集A⊆C为“决策分类不确定度约简”，若：

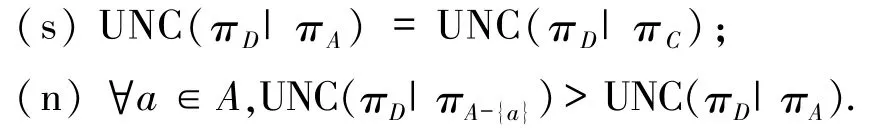
定义3提供了决策分类的不确定度，其来源于决策类粗糙度关于绝对基数比例的加权集成；该度量依托于边界结构从而成为一种基本不确定性度量，关联于知识对决策分类的解释能力［13］.不确定度能够刻画决策表的协调性.蕴含相容规则的决策表称为协调决策表，此时

此外，该度量具有粒化单调性［13］，从而定义4自然定义了“决策分类不确定度约简”.文献［13］还澄清了“决策分类不确定度约简”与“决策分类正域约简”（即代数约简）的派生关系，并依据属性重要度来开发了前向贪心约简算法.

2 特定类不确定度属性约简

在文献［13］“决策分类不确定度约简”基础上，建立“特定类不确定度约简”及其启发式约简算法，并提供相关实例说明.

2.1 约简构建为了定义“特定类不确定度约简”，需要首先确立特定类不确定度及其粒化单调性等性质.下面将决策分类不确定度进行层次分解，定义特定类不确定度.

定义5关于条件属性子集A⊆C，决策类Dj的不确度为

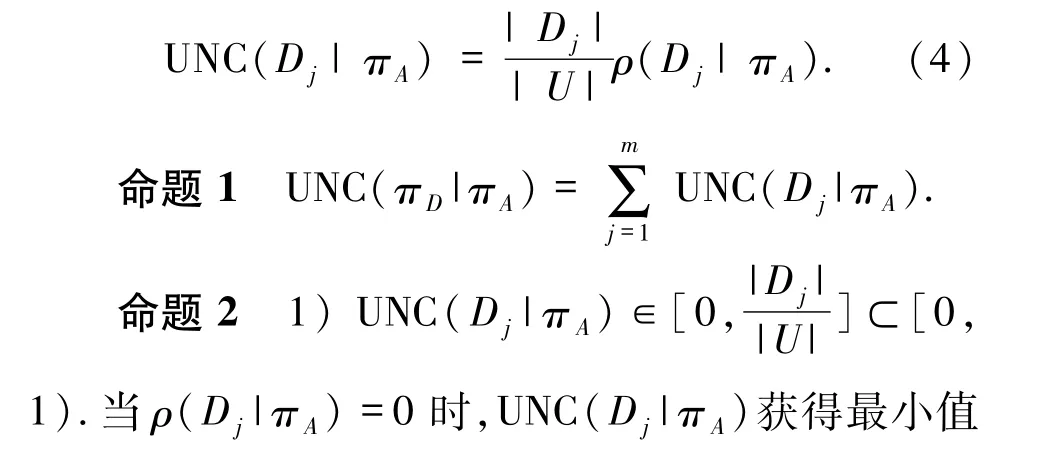
对比（3）和（4）式可见，决策类不确定度来源于决策分类不确定度的分解，而后者是关于所有决策类的层次集成（命题1）.从而，决策类不确定度具有关联于决策分类不确定度的语义与性质，但主要落实于特定决策类.

具体地，决策类不确定度是决策类粗糙度与决策类基数比例的乘积，主要关联于决策类边界从而表征不确定性，能够反向刻画知识对于决策类的解释能力，不确定度越小则解释能力越高.

命题2提供了决策类不确定度的基本性质，其相似于决策分类不确定度性质，但为后者奠定了层次基础与集成机制.其中，第1）条表明度量值域，相关的最值及其条件是显然的；第2）条依托条件属性集，揭示了决策类不确定度对于决策类协调性与不协调性的刻画，后者提出于文献［4］并用于分解决策表的协调性或不协调性；第3）条来源于粗糙度的粒化单调性，表明了决策类不确定度的粒化单调性.

基于决策类不确定度的度量语义与粒化单调性，下面提出相关的特定类约简及其算法，所建约简与存在的决策分类约简具有相似性.

定义6条件属性子集A⊆C为特定类Dj不确定度约简，若：

定义7设A⊆C且a∈C－A，属性a相对于A的重要度为

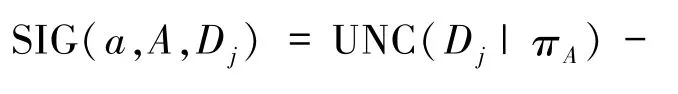
定义6提出了“特定类不确定度约简”，其中的决策类不确定度具有粒化单调性，可以用于启发式搜索.为此，定义7提出对应的属性重要度.

SIG（a，A，Dj）描述属性a加入到属性子集A之后导致的决策类Dj不确定度减少量，该度量能够体现a相对于A的重要性程度，其越大则属性重要性越大.由此，下面利用该属性重要度建立一个启发式约简算法，主要通过最大重要度寻找最优属性，以便最终快速获取一个“特定类不确定度约简”.

算法1 特定类不确定度约简算法.

输入：决策表T、关注的特定类标签j；

输出：特定类Dj不确定度约简A.

步骤1 设置A＝∅；

步骤2 计算UNC（Dj｜πC）；

步骤3 ∀a∈（C－A），计算属性重要度SIG（a，A，Dj），并靠前选择属性重要度最大的条件属性a并入A的尾部，即进行更新A←A∪｛a｝.如果此时有

算法1是一个前向贪心约简算法，其主要从空集开始增加属性，步骤3通过顺序选取最优属性让A快速满足定义6的约简充分性条件（s），而步骤4是后项删除过程，以确保A满足定义6的约简必要性条件（n），从而A是一个“特定类不确定度约简”，最终被有效输出.

2.2 实例说明提供一个决策表实例，用于分析特定类不确定度及“特定类不确定度约简”.

例1设表1所述二分类决策表T，其中

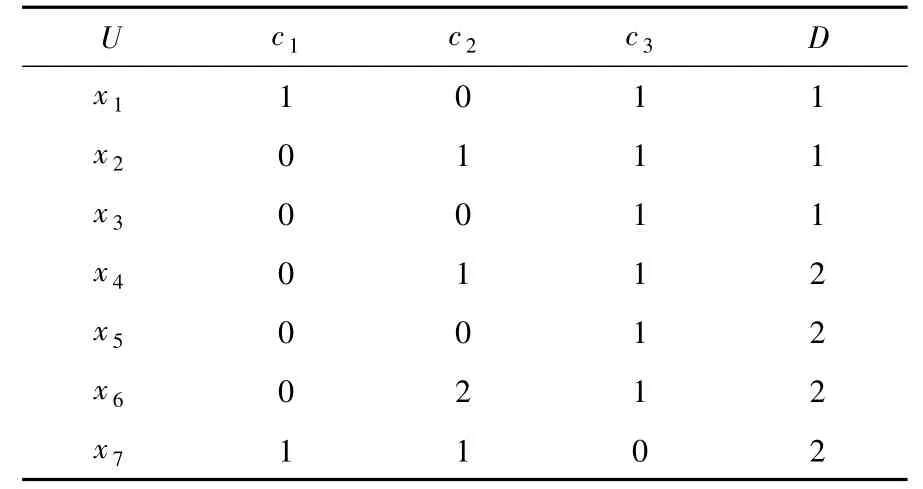
表1 实例决策1Tab.1 Example decision 1

此表是不协调的，其中的2个决策类也是不协调的.

而C的非0不确定度刚好对应决策类不协调性.此外，粒化单调性可通过属性层次链进行检验，例如：

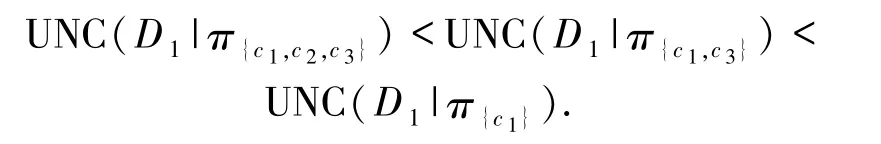
根据定义6与表2，可以得到所有“特定类不确定度”约简，即D1、D2类分别具有约简｛c1，c2｝、｛c1，c2｝.从算法1的角度来看，针对D1类，靠前选择不确定度最大的条件属性c1，其没有达到C的不确定度，此时｛c1｝的扩充有｛c1，c2｝和｛c1，c3｝2个选择，选择属性重要度最大的属性进行更新，得到A＝｛c1，c2｝，此时D1类不确定度达到C的不确定度0.34，即

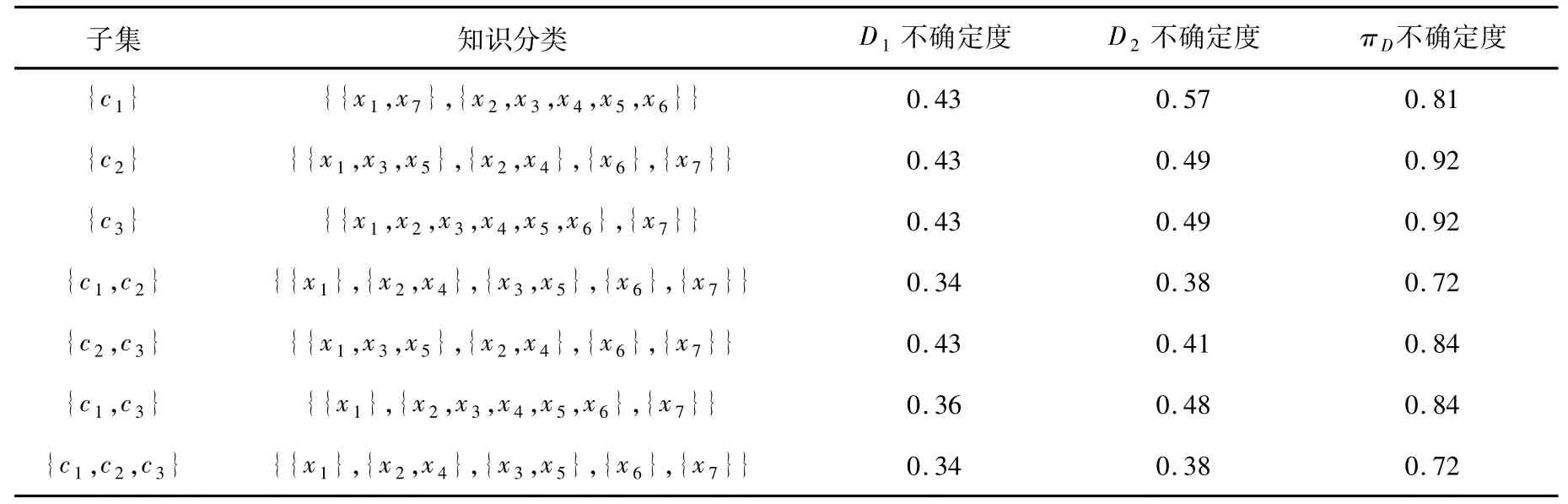
表2 基于幂集空间的不确定度Tab.2 Uncertainty degrees based on power set space

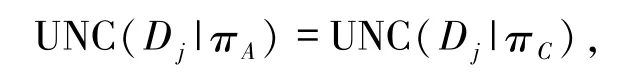
进入步骤4.向前遍历删除A中的每个属性a，有

进入步骤5，返回A，即D1类具有约简A＝｛c1，c2｝.类似可以得到D2类不确定度约简｛c1，c2｝，其与定义6计算结果一致.

3 特定类不确定度约简与2种存在约简的关系

如图1所示，下面探究“特定类不确定度约简”与“特定类正域约简”“决策分类不确定度约简”的关系，并提供相关实例分析.

3.1 约简关系首先揭示“特定类不确定度约简”与“特定类正域约简”的横向关联.

定理1若A是C“特定类Dj不确定度约简”，则

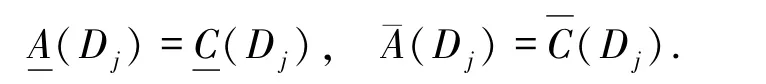
证明若A是C“特定类Dj不确定度约简”，根据定义6及（2）式，有

定理2若A是C的“特定类不确定度约简”，则A必定包含C的一个“特定类正域约简”.

证明若给定决策类是协调的，由定义6和命题2可知

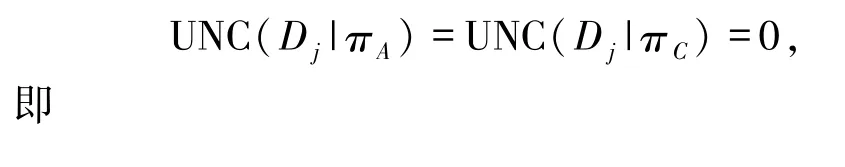
A包含C的一个“特定类正域约简”.证毕.

推论1若给定的决策类是协调的，则A是C的“特定类不确定度约简”等价于A是C的“特定类正域约简”.

证明基于单调性，约简必要条件中的元素表述式∀a∈A可以等价地修改为子集表达式∀A′⊂A，由此下面证明采用后者来叙述.

若A是C的“特定类不确定度约简”，由定理1可知

因此，A是C的“特定类正域约简”.

另一方面，若A是C的“特定类正域约简”，则

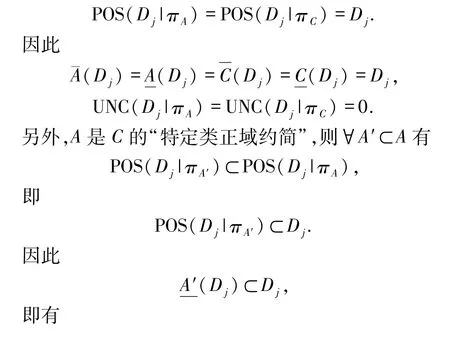
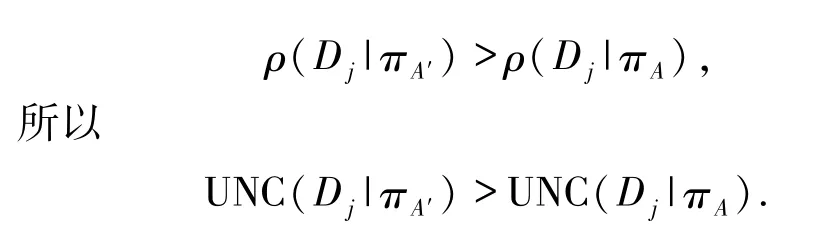
因此，A是C的“特定类不确定度约简”.证毕.

推论2若给定的决策类是不协调的，则A是C的“特定类正域约简”不一定等价于A是C的“特定类不确定度约简”.

证明由后面例2的D1决策类情况可证，证毕.

“特定类正域约简”保持正域，可能会造成边界域的扩大.基于定理1，引入的“特定类不确定度约简”能够有效保持决策类的上近似和下近似，故具有差异性与价值性.进一步，定理2提供了2种约简的关联，其中“特定类不确定度约简”更强一点.最后相关的推论1、2表明，在协调类时2种约简是等价的，不协调类才可能引起“特定类不确定度约简”强于且不同于“特定类正域约简”.

下面揭示“特定类不确定度约简”与“决策分类不确定度约简”的纵向关联.为此，2种约简集分别设为REDUNC（Dj）、REDUNC（πD）.利用文献［3］的思路与结果，可以得到如下基本结论.针对这2种约简，引理1表达约简条件的相关性，定理3表现约简的转换条件，定理4表明决策分类约简到特定类约简的派生性，定理5提供相反的特定类约简到决策分类约简的派生性.

引理1约简条件具有如下等价表示：

3.2 实例分析下面提供一个实例来计算相关约简，从而验证“特定类不确定度约简”与“特定类正域约简”、“决策分类不确定度约简”的关系.

例2设表3所述三分类决策表T，其中U＝｛x1，x2，…x12｝，C＝｛c1，c2，c3｝，D1＝｛x1，x2，x3，x4｝，D2＝｛x5，x6，x7，x8｝，D3＝｛x9，x10，x11，x12｝.

表3 实例决策2Tab.3 Example decision 2

此表是不协调决策表，其中的3个决策类都是不协调的.

根据定义（如定义2、4、6），可得2种正域约简与不确定度约简，相关的4种约简结果如表4.

表4 2种正域约简与不确定度约简Tab.4 Two types of positive region reducts and uncertainty degrees reducts

表4结果可以验证相关约简关系.针对D1类，有：

这表明“特定类不确定度约简”导致上下近似相等，这验证定理1；针对D1类，不确定度约简｛c1，c2｝和｛c2，c3｝中分别包含正域约简｛c1｝和｛c2，c3｝，这验证定理2；｛c1，c2｝是D1类不确定度约简，但不是正域约简，｛c1｝是正域约简，但不是不确定度约简，这验证了推论2的不等价性.同理可以验证其他2类情形，其中D2、D3类正域约简和不确定度约简都为｛c1｝.针对2种不确定度约简的纵向关系，主要验证相互派生的定理4与5.针对唯一决策分类不确定度约简A＝｛c1，c2｝，可以派生出分别适用于3个特定类约简：

4 结束语

针对不确定边界域相关的特定类属性约简，分解建立决策类的不确定度，进而提出“特定类不确定度属性约简”及其启发式算法，最终得到了“特定类不确定度约简”与“特定类正域约简”的横向联系以及与“决策分类不确定度约简”的纵向联系.由此，“特定类不确定度约简”改进了“特定类正域约简”，主要是在不协调决策类的情形下，同时其也为“决策分类不确定度约简”奠定了集成基础.基于不确定度的粒化单调性，还可以建立约简核概念，充当算法1的搜索起点从而提高算法搜索效率.