方程φe（φe（n））＝3Ω（n）（e＝3，4）的可解性

王爱钧， 廖群英

（四川师范大学 数学科学学院，四川 成都610066）

1 序言及主要结果

熟知，正整数n的欧拉函数φ（n）的值等于序列1，2，…，n中与n互素的整数个数［1-4］.文献［5-8］定义了正整数n的广义欧拉函数

此后，欧拉函数的研究变得更加丰富.吕志宏［9］研究了方程φ（n）＝2ω（n）和φ（φ（n））＝2ω（n）的可解性（ω（n）为正整数n的所有不同素因子个数）；马静［10］研究了方程φ（n）＝2tω（n）的可解性（t为正整数）；Zhang等［11］研究了方程φ（φ（n））＝2Ω（n）的解，并给出了该方程的全部奇数解，其中Ω（n）为正整数n的全部素因子个数（按重数计算）；田呈亮等［12］研究了方程φ（φ（n））＝2Ω（n）的可解性，并且给出了该方程的全部正整数解；俞红玲 等［13］研究了方程φ2（n）＝2ω（n）和φ2（φ2（n））＝2ω（n）的可解性，并且给出了这2个方程的全部正整数解；金明艳等［14］给出了方程φ2（n）＝2Ω（n）和φ2（φ2（n））＝2Ω（n）的全部正整数解.本文在此基础上，进一步研究方程

下面的定理1.1～1.4是对方程（1）的讨论，定理1.5～1.9则是对方程（2）的讨论.

定理1.1若αi＝0（1≤i≤k），或α≥2且αi≥1（1≤i≤k），则方程（1）无解.

定理1.2若α∈｛0，1｝且存在pi≡1（mod 3），则方程（1）有解，当且仅当α＝0，此时恰有唯一解n＝73.

定理1.3若α＝0且pi≡2（mod 3）（1≤i≤k），则如下条件之一成立时，方程（1）无解：

1）βj＝0（1≤j≤m）；

2）存在qj≡1（mod 3），或α0≥2且qj≡2（mod 3）（1≤j≤m）.

定理1.4若α＝1且pi≡2（mod 3）（1≤i≤k），则如下条件之一成立时，方程（1）无解：

1）βj＝0（1≤j≤m）；

2）存在qj≡1（mod 3），或α0≥2且qj≡2（mod 3）（1≤j≤m）.

定理1.5若αi＝0（1≤i≤k），则方程（2）无解.

定理1.6若α≥2且αi≥1（1≤i≤k），则如下条件之一成立时，方程（2）无解：

1）βj＝0（1≤j≤m）；

2）α0＝0，且βj≥1（1≤j≤m）.

定理1.7设α∈｛0，1｝且存在素数pi≡

1（mod 4）（1≤i≤k）.

1）若βj＝0（1≤j≤m），则方程（2）无解；

2）若α0＝0且βj≥1（1≤j≤m），则方程（2）的全部正整数解为n＝53 298.

定理1.8若α＝0且pi≡3（mod 4）（1≤i≤k），则如下条件之一成立时，方程（2）无解：

1）βj＝0（1≤j≤m）；

2）α0＝0，且βj≥1（1≤j≤m）.

定理1.9设α＝1且pi≡3（mod 4）（1≤i≤k），则如下条件之一成立时，方程（2）无解：

1）βj＝0（1≤j≤m）；

2）α0＝0，且βj≥1（1≤j≤m）.

2 主要结果的证明

为证明本文主要结果，需要以下几个引理.

（b）当b＝0时，等式化为（4t＋3）β－1（2t＋1）＝3，得到β＝1，t＝1，或β＝2，t＝0.又由于β为奇数，故β≠2，即β＝1，t＝1，则q＝7.

2）当β为偶数时，原方程等价于（4t＋3）β－1（2t＋1）＝2·3b－1.

（a）当b≥1时，等式两边模3得到tβ－1（2t＋1）≡2（mod 3）.于是

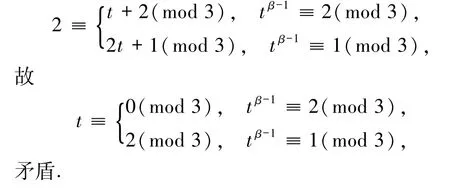
（b）当b＝0时，等式化为（4t＋3）β－1（2t＋1）＝1，得到β＝1且t＝0，与β为偶数矛盾.

综上可知，原方程有唯一解β＝1，b＝0且q＝7.

（b）若β≥1且βj＝0（1≤j≤m），则φ3（n）＝2α03β.若β＝1，则φ3（n）＝3·2α0.故由（3）式以及引理2.1知均为偶数.又由3Ω（n）为奇数，可知φ3（φ3（n））≠3Ω（n），故方程（1）无解.

定理1.2的证明1）当α＝0且存在pi≡1（mod 3）时，由引理2.1知

由于存在pi≡1（mod 3），即存在pi－1（1≤i≤k）为偶数，再由于qj是奇素数，可知α0≥1.

（a）若β＝βj＝0（1≤j≤m），则φ3（n）＝2α0.若α0＝1，则φ3（n）＝2.由（4）式得k＝1，p1＝7，且α1＝1，故n＝p1＝7且φ3（φ3（n））＝0.从而Ω（n）＝α1＝1，故3Ω（n）＝3≠0，即方程（1）无解.故α0≥2，则由（4）式及引理2.1可知

均为偶数.又由3Ω（n）为奇数可知φ3（φ3（n））≠3Ω（n），故方程（1）不成立.

（d）若β≥1且βj≥1（1≤j≤m），则由（4）式及引理2.1得

均为偶数.又由3Ω（n）为奇数可知φ3（φ3（n））≠3Ω（n），故方程（1）不成立.

2）当α＝1且存在pi≡1（mod 3）时，由引理2.1知

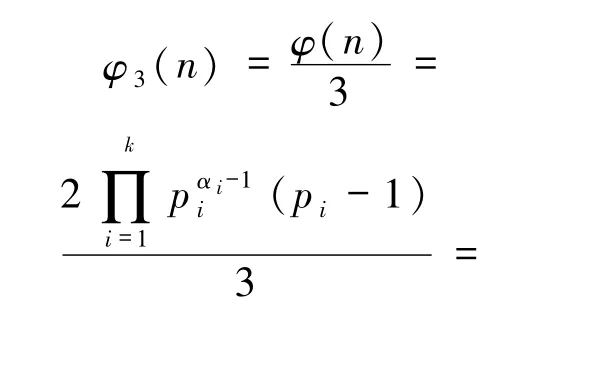
由于φ3（n）含有一个因子2，又存在pi≡1（mod 3），即存在pi－1（1≤i≤k）为偶数，故α0≥2.

（a）若β＝βj＝0（1≤j≤m），则φ3（n）＝2α0.从而由（5）式及引理2.1知

故方程（1）无解.

（d）若β≥1且βj≥1（1≤j≤m），则由（5）式及引理2.1得

均为偶数.又由3Ω（n）为奇数可知

φ3（φ3（n））≠3Ω（n），故方程（1）无解.

定理1.3的证明当α＝0且任意pi≡2（mod 3）时，故由引理2.1知

又3Ω（n）为奇数，故由方程（1）可知α0＝1，且3Ω（n）＝1，即Ω（n）＝0，故n＝1，此时φ3（φ3（1））＝0，矛盾.

定理1.4的证明当α＝1且任意pi≡2（mod 3）时，则由引理2.1知

1）若βj＝0（1≤j≤m），则φ3（n）＝3α0（α0≥0），故由广义欧拉函数的定义及引理2.1可知

又3Ω（n）为奇数，故由方程（1）知α0＝1且3Ω（n）＝1，即Ω（n）＝0，故n＝1，此时φ3（φ3（1））＝0，矛盾.

2）若存在qj≡1（mod 3）或α0≥2，且qj≡2（mod 3）（1≤j≤m），则由（7）式及引理2.1知

即方程（1）无解.

定理1.5的证明当αi＝0（1≤i≤k）时，n＝2α（α≥0），则由广义欧拉函数的定义及引理2.2可知

又由定义可知Ω（n）＝α，故3Ω（n）＝3α.由以上可知φ4（φ4（n））≠3Ω（n），故方程（2）无解.

定理1.6的证明当α≥2且αi≥1（1≤i≤k）时，由引理2.2知

又3Ω（n）为奇数，故由方程（2）可知α0＝2或3，且3Ω（n）＝1，即Ω（n）＝0，故n＝1，此时φ4（φ4（1））＝0，矛盾.

由等式两边奇偶性可知m＝1.当n＞4时，Ω（n）≥1，此时（9）式等价于

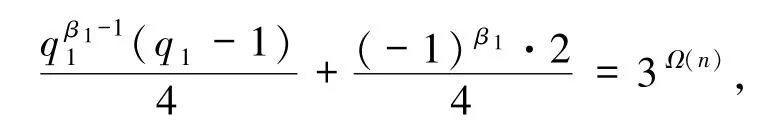
再由引理2.4知其无解，即方程（2）不成立.故必存在qj≡1（mod 4）（1≤j≤m），此时由（8）式及引理2.2知

若α1＝1，则由（10）式可知p1＝219＝3×73，与p1为素数矛盾，即方程（2）无解.

因此，α1≥2，此时若p1＝31，则断言

事实上，当α1＝2时，（11）式左边等于465，右边等于325，即（11）式成立.现设α1＝k时，（11）式成立.则α1＝k＋1时，

故（11）式成立.进而，若p1≥31，则由（11）式可得

即（10）式不成立.故p1＜31，又p1≡3（mod 4）为素数，故p1＝3，7，11，19，23.

p1＝3时，（10）式等价于3α1－1＝4·3α1＋2＋1，明显不成立.p1＝7时，（10）式等价于3·7α1－1＝4·3α1＋2＋1.易知α1＝2，3，4，5，6时，（10）式的左边等于21、147、1 029、7 203、50 421，相应的右边等于325、973、2 917、8 749、26 245，显然不成立.当α1≥7时，对α1作归纳证明，可知（10）式的左边恒大于右边，矛盾.p1＝11时，（10）式等价于5·11α1－1＝4·3α1＋2＋1.α1＝2，3，4时，（10）式的左边等于55、605、6 655，相应的右边等于325、973、2 917，显然不成立.当α1≥5时，对α1作归纳证明，可知（10）式的左边恒大于右边，仍然矛盾.p1＝19时，（10）式等价于9·19α1－1＝4·3α1＋2＋1.容易计算得到：α1＝2，3时，（10）式的左边等于171、3 249，相应的右边等于325、973，显然不成立.当α1≥4时，对α1作归纳证明，可知（10）式的左边恒大于右边，矛盾.p1＝23时，（10）式等价于11·23α1－1＝4·3α1＋2＋1.α1＝2，3时，（10）式左边等于253、5 819，相应的右边等于325、973，显然不成立.当α1≥4时，对α1作归纳证明，可知（10）式的左边恒大于右边，矛盾.

综上可知，方程（2）无解.

定理1.7的证明当α∈｛0，1｝且存在pi≡1（mod 4）（1≤i≤k）时，由引理2.2知

1）若βj＝0（1≤j≤m），则φ4（n）＝2α0（α0≥0），由广义欧拉函数的定义及引理2.2可知

又3Ω（n）为奇数，故由方程（2）可知α0＝2或3，且3Ω（n）＝1，即Ω（n）＝0，故n＝1，此时φ4（φ4（1））＝0，矛盾.

2）若α0＝0且βj≥1（1≤j≤m），则

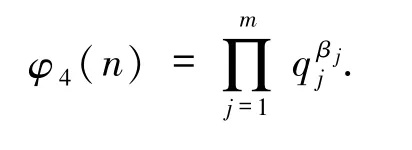
若qj≡3（mod 4）（1≤j≤m），则由引理2.2知

由等式两边奇偶性可知m＝1.当n＞4时，Ω（n）≥1，此时（13）式等价于

再由引理2.4知其无解，即方程（2）不成立.故必存在qj≡1（mod 4）（1≤j≤m），此时由（12）式及引理2.2知

事实上，α1＝2时，（15）式的左边等于39，右边等于37，即（15）式成立.现设α1＝k时（15）式成立.则α1＝k＋1时，

故（15）式成立.注意到p1≥13时，由（15）式可得

p1＝5时，由（16）式可知方程等价于5α1－1＝4·3α1＋1＋1.α1＝2，3，4，5，6，7，8，9时，（16）式左边等于5、25、125、625、3 125、15 625、78 125、390 625，相应的右边等于109、325、973、2 917、8 749、26 245、78 733、236 197，显然不成立.而α1≥10时，对α1作归纳证明可知（16）式的左边恒大于右边，仍然矛盾.故p1＝13，此时（16）式等价于3·13α1－1＝4·3α1＋1＋1.α1＝2，3时，（16）式左边等于39、507，相应的右边等于109、325，显然不成立.而α1≥4时，对α1作归纳证明，可知（16）式的左边恒大于右边，矛盾.

综上可知，方程（2）无解.

定理1.8的证明当α＝0且任意pi≡3（mod 4）（1≤i≤k）时，由引理2.2知

1）若βj＝0（1≤j≤m），则φ4（n）＝2α0（α0≥0），由广义欧拉函数的定义及引理2.2可知

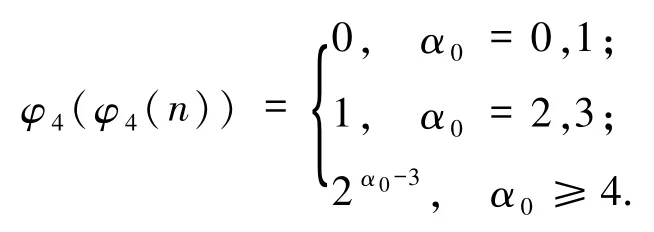
又3Ω（n）为奇数，故由方程（2）可知α0＝2或3，且3Ω（n）＝1，即Ω（n）＝0，故n＝1，此时φ4（φ4（1））＝0，矛盾.

2）若α0＝0且βj≥1（1≤j≤m），则

从而，β1＝1，q1＝4·3Ω（n）＋1，此时由（18）式得

若α1＝1，则由（20）式得到n＝p1＝55＝5·11，与p1为素数矛盾，即方程（2）无解.

因此，α1≥2，此时若p1＝19，则断言

事实上，α1＝2时，（21）式的左边等于86，右边等于37，即（21）式成立.设α1＝k时（21）式成立，即

α1＝2，3，4时，（20）式的左边等于11、73、515，相应的右边等于37、109、325，显然不成立.而α1≥5时，对α1作归纳证明可知（20）式的左边恒大于右边，仍然矛盾.故p1＝11，此时（20）式等价于

综上可知，方程（2）无解.

定理1.9的证明当α＝1且任意pi≡3（mod 4）（1≤i≤k）时，由引理2.2知

故m＝1，即

即（24）式不成立.故p1＜23，又p1≡3（mod 4）为素数，故p1＝3，7，11，19.

综上可知，方程（2）无解.

3 小结

基于φe（n）（e＝3，4）的准确计算公式，利用初等的 方 法 和 技 巧，研 究 了 方 程φe（φe（n））＝3Ω（n）（e＝3，4）的n的某些特定限制条件下的正整数解.对于n的其它分类情况，还有待进一步研究.