方程S（SL（n））＝φe（n）（e＝3，4，6）的可解性

王慧莉， 廖群英， 杜 珊

（四川师范大学 数学科学学院，四川 成都610066）

1 引言及主要结果

早在18世纪，杰出数学家欧拉就提出了著名的欧拉函数的概念.正整数n的欧拉函数φ（n）定义为序列1，2，…，n－1中与n互素的整数个数［1］.该函数在数论中具有重要的地位，并且在研究数论函数方程中应用十分广泛，早在20世纪70年代，欧拉函数就成为RSA公钥密码体制得以建立的重要数学工具之一.欧拉函数的出现引发了数学界对含有欧拉函数的数论方程的广为探讨.2002—2007年，Cai等［2］将欧拉函数进行推广，提出了广义欧拉函数的概念.对任意给定的正整数e，正整数n的广义欧拉函数φe（n）定义为序列中与n互素的数的个数，即

后来，人们根据Smarandache函数定义了伪Smarandache函数Z（n）和Smarandache LCM函数.其中，Smarandache LCM函数SL（n）定义为最小的正整数m，使得1，2，…，m的最小公倍数能被n整除［11］，即

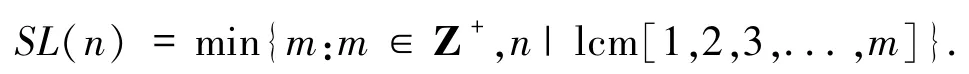
关于Smarandache函数的性质的研究，已有一些结果.例如：罗文力等［12］研究了Smarandache函数的准确计算公式以及相关数论方程，白海荣等［13］给出了Smarandache函数S（pα）的准确计算公式，并且给出了Smarandache函数的几类推广函数及其性质.基于Smarandache函数的性质，有很多关于Smarandache函数相关的方程问题的研究［14-18］.张利霞等［19-20］研究了函数方程S（SL（n））＝φe（n）（e＝1，2）的可解性，并得出它的所有正整数解；文献［21-22］研究了数论函数方程S（SL（n2））＝φe（n）（e＝1，2）的可解性，并得出它的所有正整数解；等等.最近，廖群英等［23］研究了函数方程S（SL（n2））＝φ3（n）的可解性，并给出了其全部正整数解.本文在此基础上，进一步讨论数论函数方程的问题，利用已有的广义欧拉函数的计算公式，讨论当e∈｛3，4，6｝时，广义欧拉函数与Smarandache函数S（n）和Smarandache LCM函数SL（n）的复合函数之间的关系，旨在讨论当e∈｛3，4，6｝时，数论函数方程

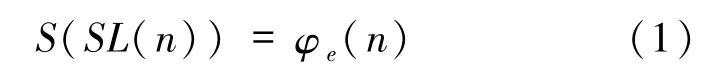
的可解性，并给出其全部正整数解，即证明如下主要结果.

2 相关引理

为叙述方便，设n为正整数，记Ω（n）为n的素因子个数（重复计数），ω（n）为n的不同的素因子的个数，并规定Ω（1）＝ω（1）＝0.为证明本文主要结果，需要以下几个引理.

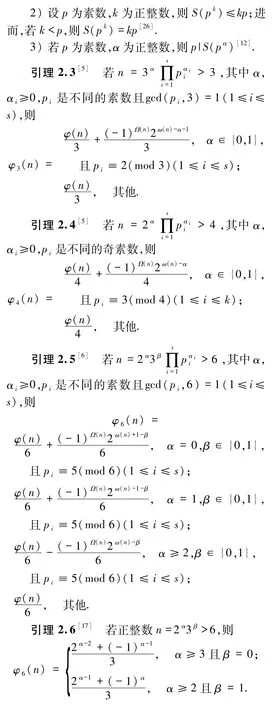
3 主要结果的证明

定理1.1的证明可直接计算知，n＝1，2，3均不是方程（1）的解.

综上所述，定理1.1得证.

定理1.2的证明可直接计算知，n＝1，2，3，4均不是方程（1）的解.

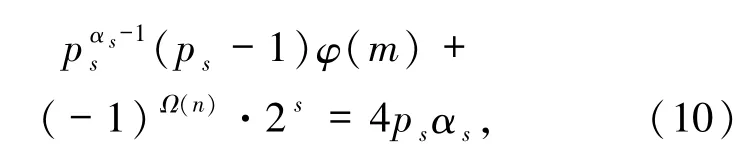
比较两边ps的个数可得αs＝1，此时（10）式即为（ps－1）φ（m）＋（－1）Ω（n）·2s＝4ps.又ps为奇素数，不妨设ps－1＝2r t，其中r≥1，gcd（2，t）＝1.此时（10）式即为

当r≥2时，显然s≥2，此时φ（m）为偶数，则方程（11）即为

对比（13）式两边的奇偶性可知s＝2，即2r－2tφ（m）＝2r t＋1＋（－1）Ω（n）＋1.若Ω（n）为偶数时，则2r－2tφ（m）＝2r t，即φ（m）＝4，故m＝5，8，10，12，相应地，n＝5ps，23ps，2×5ps，22×3ps，与题设矛盾.故Ω（n）为奇数，则2r－2tφ（m）＝2r t＋2，故2r－2t｜2，即t＝1，r＝2，3，此时ps＝5或9，与题设矛盾.

4 小结与展望

本文基于Smarandache函数、Smarandache LCM函数基本性质，以及φe（n）（e＝3，4，6）的准确计算公式，利用初等的方法和技巧，研究了数论方程S（SL（n））＝φe（n）（e＝3，4，6）的可解性，并确定了其全部正整数解.对于e＝3，4，6的情形，后续可以研究方程S（SL（n2））＝φe（n）（e＝3，4，6）的正整数解问题.