无限时滞随机泛函微分方程的一般衰减ψγ-稳定性

刘 羽， 李树勇

（1.四川师范大学 数学科学学院，四川 成都610066； 2.绵阳师范学院 数理学院，四川 绵阳621000）

随机泛函微分方程稳定性由于在实际应用中的重要作用长期被学者们所关注，各种稳定性，如指数稳定性、多项式稳定性、对数稳定性等被提出，相应的稳定性判定定理被建立［1-5］.针对不同的稳定性，Liu［6］提出了ψγ-稳定性概念，涵盖了上述各类稳定性，并建立了一系列稳定性结果.Razumikhin方法是一种重要的技巧，在随机泛函微分方程稳定性研究中发挥了重要的作用.从Mao［4］首先将Razumikhin技巧运用于随机泛函微分方程建立随机版本的Razumikhin型稳定性定理以来，学者们运用Razumikhin方法建立了各类随机泛函微分方程的Razumikhin稳定性定理［7-12］.如Liu等［9］运用Razumihin技巧研究具有无穷时滞的随机泛函微分方程稳定性，建立了该系统的Razumikhin型p阶矩ψγ稳定性定理和a.s.ψγ稳定性定理.然而，这些Razumikhin型定理通常是通过标量微分不等式描述的，但是，许多系统是多维的，因此使用分量Lyapunov函数方法研究随机微分方程的稳定性引起学者们的关注［13］，最近Liu［14］利用随机分析技巧和M矩阵性质建立随机泛函微分系统p阶指数稳定的分量Razumikhin型定理.Liu等［15］利用Razumikhin技巧和分量Lyapunov函数讨论随机泛函微分方程的输出状态稳定性，建立该随机泛函微分方程的Razumikhin型p阶矩指数输出状态稳定性定理.受他们思想的启发，本文将讨论一类具有无限时滞随机微分方程的具有一般衰减率的稳定性问题，利用Razumikhin技巧和分量Lyapunov函数方法，建立系统具有一般衰减率的p阶矩ψγ-稳定性和a.s.ψγ-稳定性定理，丰富了随机泛函微分方程稳定性的理论.

1 基本准备

设G为一个向量或矩阵，用G≥0表示G中所有元素非负，G≫0表示G中每个元素都为正.此外，记Zn×n＝｛A＝（aij）n×n：aij≤0，i≠j｝.若存在向量x≫0，使得矩阵Ax≫0，则称矩阵A∈Zn×n是一个非奇异M-矩阵.记ΩM（A）＝｛x∈Rn｜Ax≫0，x≫0｝.

2 主要结论

引理2.1若存在W1，…，Wn∈C1，2（R×Rd；R＋）满足以下条件：

（i）存在v∈K，使得

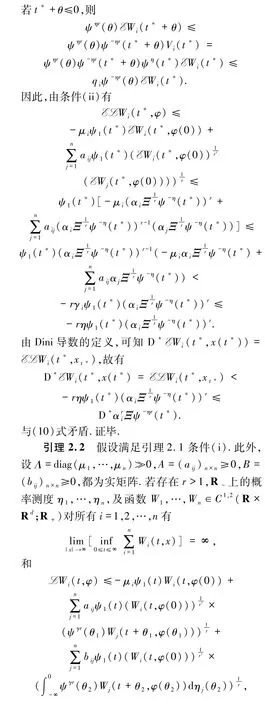
与（17）式矛盾.故对任意t≥0，有（12）式成立，得证.

定理2.3假设引理2.2的条件全部满足，并且存在常数C，p＞0，使得

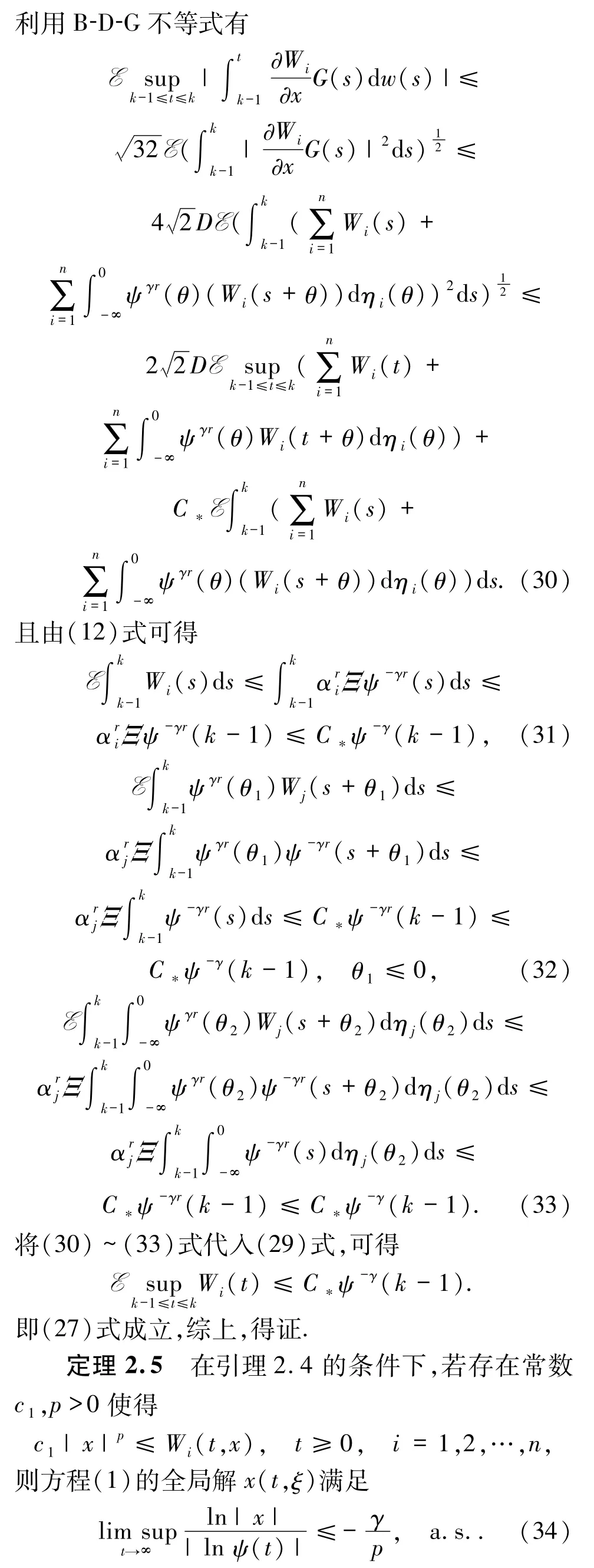
3 例子和数值模拟

计算可知μ－A是一个非负的M-矩阵，若取α1＝1，α2＝1.2，此时γ2＝0.032.由定理2.3可得，系统（25）的解x（t）是2阶矩ψγ-稳定的.

例子3.2令t≥0，考虑如下2维非自治系统

计算可知μ－（A＋B）是一个非负的M－矩阵，若取α1＝1，α2＝2，此时γ6＝0.050.

由于W1＋W2≥｜x1｜3或者｜x2｜6，所以由定理2.3知，系统（27）的平凡解关于x1是3阶矩ψγ-稳定，x2是6阶矩ψγ-稳定.