再谈数列一个性质的证明
2023-01-16 02:23江苏省昆山中学215300季刚祥吴祖燕
中学数学研究(江西) 2023年2期
江苏省昆山中学 (215300) 季刚祥 吴祖燕
性质如果各项均为正数的等比数列和一个等差数列,首项、末项、项数分别相等,那么等比数列的各项均不超过等差数列的对应项.
文[1]中,运用函数思想通过恰当的换元,将上述数列问题转化为一个与幂函数相关的不等式问题来解,并给出了函数不等式的几何解释.让读者既能感受到思路的巧妙、解法的合理又能体会到几何的直观,真的受益匪浅.在研读文[1]的过程中,笔者又得到了上述性质的另两种证法,现陈述如下,供大家参考.
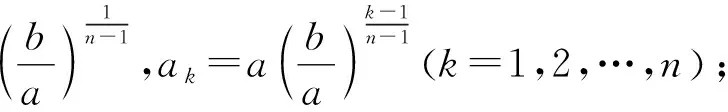
易知p=1,即a=b及x=0,即k=1以及x=1,即k=n时,不等式取等号.下证当p>0且p≠1,0 图1 (3)式是“指数函数y=px的图像在(0,1)这一段曲线上的任意一点P(x,px)与点Q(0,1)连线的斜率恒小于过曲线的两个端点(0,1)和(1,p)的弦的斜率”.因为y=px是凹函数,所以上述结论成立如图2所示. 图2 评注:(1)上述两种证法的共同点都是将数列 不等式转化为函数不等式来解决,揭示了事物的特殊性寓于普遍性这一辩证思想,解题的关键是巧妙变形、合理换元、科学构造,体现了化归转化及函数等基本的数学思想方法,同时两种解法的几何解释又从形的角度直观明了地验证了通过逻辑推理得到的数学事实.

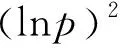


猜你喜欢
中学生数理化·七年级数学人教版(2021年12期)2021-12-31
新世纪智能(数学备考)(2021年9期)2021-11-24
新世纪智能(数学备考)(2021年9期)2021-11-24
新世纪智能(数学备考)(2020年9期)2021-01-04
天府数学(2020年3期)2020-09-10
河北理科教学研究(2020年1期)2020-07-24
中学教学参考·理科版(2017年8期)2018-02-24
中学生数理化·高三版(2017年2期)2017-04-21
福建中学数学(2017年1期)2017-04-21
福建中学数学(2016年8期)2016-12-03

