一道高三模拟题的思路探究与拓展*

江苏省海门中学 (226100) 樊陈卫

一、问题给出

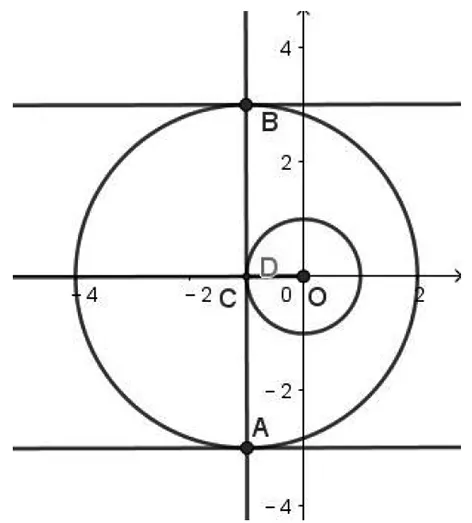
图1

图2

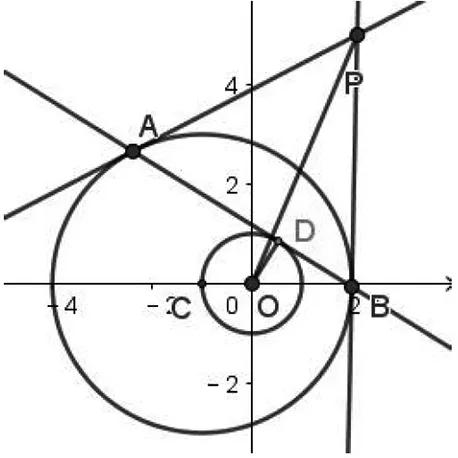
图3

对于本题的命题意图与学生临场表现的出入，作为任课教师，笔者首先感到欣慰的是学生没有被压轴题的位置所吓到，而是敢于面对勇于胜利，也贯彻了善于从特殊情形探索问题的结论和解决问题的思路这个数学思想方法.同时作为考后回顾，也有必要带领学生对这道题目进行深入的探究，获得对问题的本质理解.

二、结论证明

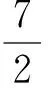
师：困难在于线段OP的长与点A、B为切点不容易直接关联，如何利用“点A、B为切点”这一条件？

生：应该连接CA、CP，CP与AB交点为M.如图4.

图4

师：很好，结合“点A、B为切点”这个条件看看有什么发现？

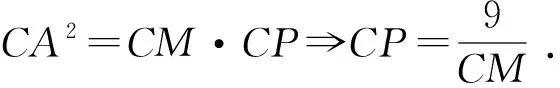
师：能不能先确定CM的范围，进一步确定CP的范围？

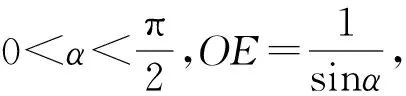
师：很好，这个结论从图上看显而易见，但说清楚逻辑关系也要费一番功夫的，它对我们要解决的问题有帮助吗？我们要求的是OP的最小值.

生：再考虑CP与OP的关系：OP≥CP-OC=CP-1.

师：CP与OP的关系还有其它的表达方式，由求解的问题确定选择上述关系.

师：很好.这个解法中CP连接已知和所求的桥梁，大家可以从CP的作用体会解题的思路.另外，从前面的解题过程中大家能感觉到动点P的轨迹是什么曲线吗？

生：感觉CP的长可以是无穷的，有可能是抛物线或双曲线？

师：到底是不是抛物线或双曲线，需要求出轨迹方程，要从解析几何的角度去探究了.

三、轨迹方程

思路1 直线l于圆O是切线，对于圆C是关于圆外点P的切点弦，可以从这两个角度表示出直线l的方程，解法如下：

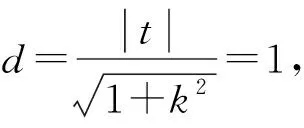
思路2 以CP为直径构造圆，由PA、PB为圆C的切线可得AB为两圆的相交弦，从而得到直线AB方程.

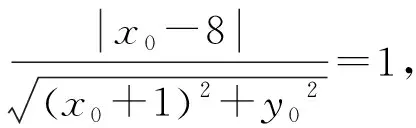
两个解法求轨迹方程的总体思路相似，都是设出动点坐标，再利用条件建立含有动点坐标的方程.区别之处是解法1直接由已知条件出发，思路比较自然，计算稍显繁琐；解法2巧妙构造圆方程，使得计算简捷明了.进一步思考如果两圆圆心重合，易得动点P的轨迹为圆，随着两圆情况的变化，动点P的轨迹如何变化？

四、圆锥曲线

要弄清各种情形下动点P的轨迹，需要对原问题进行一般化：

当a=r时，圆C的圆心在圆O上，轨迹方程①为抛物线r2y2-2aR2(x-a)-R4=0；

五、教学启示

这道题的解题教学过程给笔者如下启示：

首先教师不能只看学生解题结果对错，而是应该关注学生面对问题是怎么想的，做对了是怎么做对的，做错了是什么原因做错的，摸清了学生解题过程中的思维亮点和断点，教师的解题教学才能有的放矢，有明确的针对性.其次，解题教学中，教师要注意引导学生思考的艺术性，针对学生的思维断点，给学生指导下的普适性的提示，让学生能在师生的思维交流中有自己的思考活动.最后，教师应该认识到，高考题大多是将一般性问题特殊化，具体化，只要做好对问题的特殊性与一般性分析，看高考题就能把握其本质.