数列通项公式求法探秘
⦿广东省东莞市第七高级中学
马洪博
1 引言
研究数列问题,首先要研究数列的通项公式,当一个数列的通项公式确定后,这个数列的所有性质都可“浮出水面”.然而,数列的通项公式,如同函数的解析式一样,并非可轻而易举取得,需具体问题具体分析,并选择恰当的方法才可求出.求数列的通项公式有哪些基本方法?对此,笔者作了些肤浅的研究,并归纳出下文中的几种方法.
2 公式法
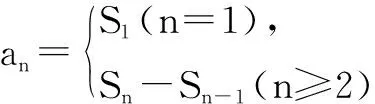
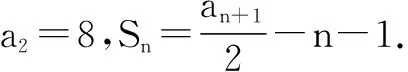
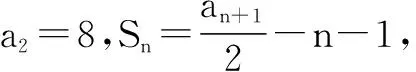
又因为a2=8=3a1+2,所以an+1=3an+2,n∈N*,于是an+1+1=3(an+1),故数列{an+1}是等比数列,且首项为a1+1=3,公比为3.所以an+1=3×3n-1=3n,故an=3n-1.
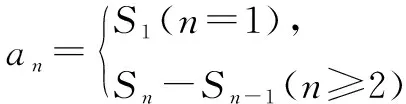
3 累加法
当已知数列中出现形如递推关系式an-an-1=f(n)(n≥2)时,一般可采用累加法求其通项公式,具体步骤:先对递推关系式an-an-1=f(n)(n≥2)中的n赋值,从2开始,一直赋值到n,于是共得到n-1个等式,然后将这n-1个等式的左右两边对应相加,并加以化简,再利用已知的首项,就可以求得数列{an}的通项公式.
例2已知数列{an}满足an+1=3an+2×3n+1,a1=3,求数列{an}的通项公式.
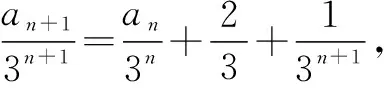
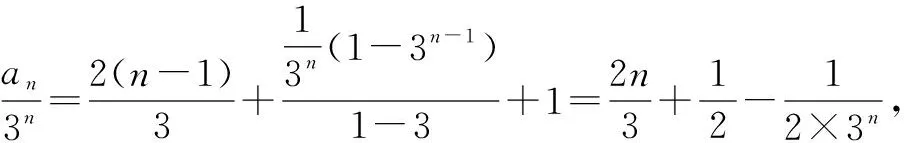
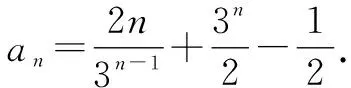
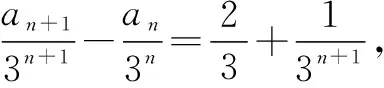
4 累乘法
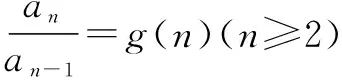
例3如果数列{an}满足an+1=2(n+1)5n×an,且a1=3,则数列{an}的通项公式是______.
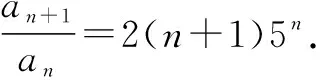
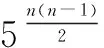
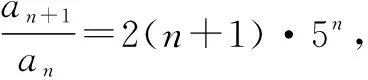
5 归纳法
观察、归纳、猜想、论证是数学研究的一般方法,这种方法也可以用在数列通项公式的求法上.探究时需先从特殊到一般,再从一般回到特殊.而猜想的结论的论证一般需用到数学归纳法.因此,这种解法还需要我们熟练掌握数学归纳法的原理和应用.
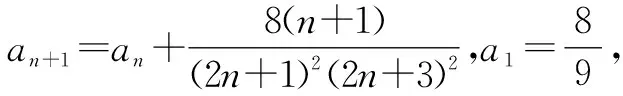
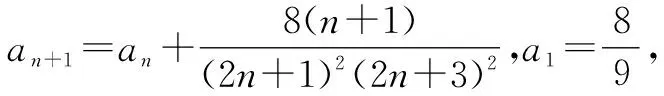
①
下面用数学归纳法证明这个猜想.
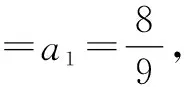

即当n=k+1时,猜想也成立.
根据(1)(2)可知,猜想对任何n∈N*都成立.
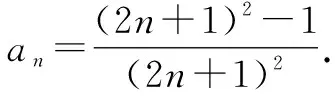
点评:先猜后证,是这种方法的基本思路,“猜”考查的是观察能力与归纳能力,“证”则考查了逻辑推理能力.这种方法较能体现数学核心素养,因此这类问题备受命题者青睐.
6 总结
当然,数列通项公式的求法还有很多,如对数变换法、迭代法、换元法和不动点法等,但无论哪种方法都并非凭空产生,只有认真审题,抓住题中给出的递推关系式的特征,才能发现与之相匹配的求解思路与解题方法.

