在质疑中提升思维的质量—一道关于圆的方程高考题的讲评
⦿湖南省宁乡市第一高级中学
唐新阳
1 问题的产生
在一次高三第一轮复习调研考试中,命题者采用了1997年的全国高考第25题.原题如下:
设圆满足:(1)截y轴所得弦长为2;(2)被x轴分成两段圆弧,其弧长的比为3∶1.在满足条件(1)(2)的所有圆中,求圆心到直线l:x-2y=0的距离最小的圆的方程.
本次调研中此题的得分率很低,因此,笔者针对这个题进行了讲评.
2 讲评的过程
由于学生已经做过,笔者先引导大家学习了该题的一个标准答案(参考答案中的一个答案).
解:设圆心C(a,b),半径为r,则可设圆的标准方程为(x-a)2+(y-b)2=r2.
由条件(1)可知
r2-a2=1
①
由条件(2)可知,劣弧所对的圆心角为90°,得
r2=2b2
②
由①②式知,2b2-a2=1
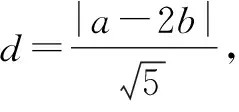
所以,圆的方程为(x-1)2+(y-1)2=2,或(x+1)2+(y+1)2=2.
2.1 质疑产生
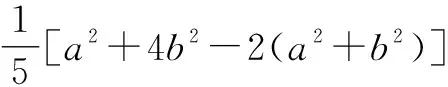
学生A:老师,我觉得这里利用重要不等式a2+b2≥2ab求d的最小值时,有很大的巧合性.如果将题目进行改动,则完全不是这种情况.
这时,教室里一阵哗然,因为他提出的想法是在直接质疑参考答案的科学性.同学们纷纷开始讨论.
师:好,请谈谈你的改动.
学生A:我们不妨把直线方程改为x-3y=0,得
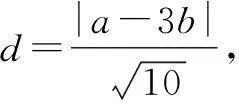
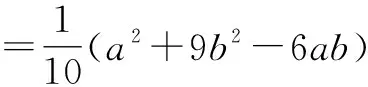
而这里-2a2+6b2不是定值,因此,这样是求不出d的最小值的.
看到这个结论,同学们开始思考这个问题更一般的解决方法.
2.2 问题的讨论与解决
学生B:老师,我找到了原题的一种更一般的解法.
学生B的解答如下:
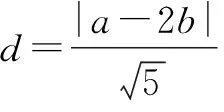
将a2=2b2-1代入整理,得
③
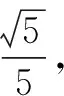
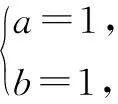
所以,圆的方程为(x-1)2+(y-1)2=2,或(x+1)2+(y+1)2=2.
学生B:这种解法对直线方程为x-3y=0也同样适用.这里我为什么这样做呢,因为平方不能解决根本问题,而去绝对值的方法除平方外还可以直接用定义,这里消元以后就转化为常见的一元二次方程在实数范围内恒有解的问题,从而淡化了这个题利用不等式解题的技巧性思路,是一种通法.
师:很好,你在质疑的过程中,将一个最值问题转化为二次方程有解的问题,利用判别式来求最值,这是我们处理含有二次式的最值问题常用的方法.只是要注意二次方程是在给定的变量范围内有解,这是一个常规方法,但要注意使用的条件.

因为2b2-a2=1,故可令
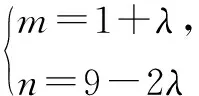
④
由ma2+nb2≥6ab,得mn=9.
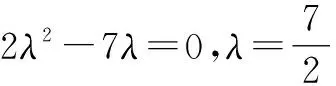
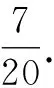
对于原题我们也可以用这个更一般的解法.
师:你的想法十分大胆,也十分有见地,能够将不等式的形式作出变形推广,利用待定系数法,凑配出定值,通过定值成立建立方程求解,这也是我们有时利用不等式求最值时常要用到的变形技巧.
此时同学们对学生A的解答交口称赞,投来佩服的目光.
学生C:假如我们得到的关于λ的方程没有实数解或者有两个都不为0的实数解怎么办呢?
同学们开始讨论,有人动笔计算其它不同的变式.最后学生A补充:事实上,不论怎么改,只要这个方程有解,它总是一个正数解和一个0.只不过暂时还没能证明,但我相信能证明出来.因为这个过程中的数量关系是等价转化的.
学生的积极性再一次被调动,学生D:A,B同学的方法很好,但我将圆的问题再一次回到几何中去处理,有一个很好的解释.这里注意到2b2-a2=1,而a,b分别是圆心C的横坐标与纵坐标,易知圆心C的轨迹方程为2y2-x2=1,可以将问题转化为求双曲线2y2-x2=1上到直线x-2y=0距离最小的点的坐标.不妨设有直线x-2y=k,则当该直线与双曲线相切时,这个切点即为点C.解答如下:
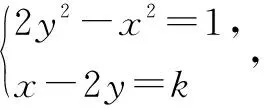
令Δ=8k2-8=0,得k=±1.
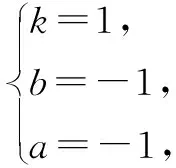
师:你的这种利用解析思想处理代数最值的方法很巧妙.有时我们得到二元变量的方程或不等式时,可以考虑是否能转化为平面内的曲线或区域,再去考虑要求的二元变量运算式所表示的几何图形与曲线或区域的位置关系,从而得到最值.
3 教后反思
本节课笔者只开了个头,但受到了同学们的质疑.在质疑过程中,同学们自主而又巧妙地解决这个问题.在这个过程中,学生思维得到了充分的“锻炼”,揭示了问题的本质,提升了解题能力.而笔者在反思教学过程时不禁想到,我们在对一节课进行预设时经验当然有很大的作用,但仅凭经验而不考虑学生思维实际以及学生能力的教学预设都是不成功的.这也同时提醒笔者,教学预设要多想几个“为什么”.

