高中数学错题管理实证探究

⦿福建省福安市第一中学

阮金锋

1 引言

错题管理指学生在遇到错题时，持有积极的态度，不逃避，并能及时、有效地采取一定的措施和策略对自己做错的题进行分析、归类等，从错误中学习，让错题发挥最大价值．

随着高中数学课程改革不断深化，数学核心素养的培养已成为当今教学的主旋律，核心素养是数学的灵魂，是课程目标的集中体现．数学学科素养有：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析．

在此背景下，本文探讨在高中数学学习中如何进行科学的、积极的、主动的、渗透核心素养的错题管理，以真正落实、提升学生的数学核心素养.

2 错题管理原则

(1)可操作性原则.错题管理是个系统管理工程,需要科学、可操作的管理方法与策略.

(2)关注、渗透核心素养原则．核心素养与错题反思相结合，相辅相成，错题管理中关注核心素养，通过错题反思提升核心素养．

(3)典型性原则．在错题管理中，没必要整理所有的错题，而只对典型错题进行整理便可．

3 错题管理策略

错题管理不是简单的订正，而是一个可操作的系统工程．其系统各环节密不可分、紧密相连、又相互影响，且渗透核心素养[1].笔者经过长期的教学实践，总结出一套错题管理策略流程，如图1：

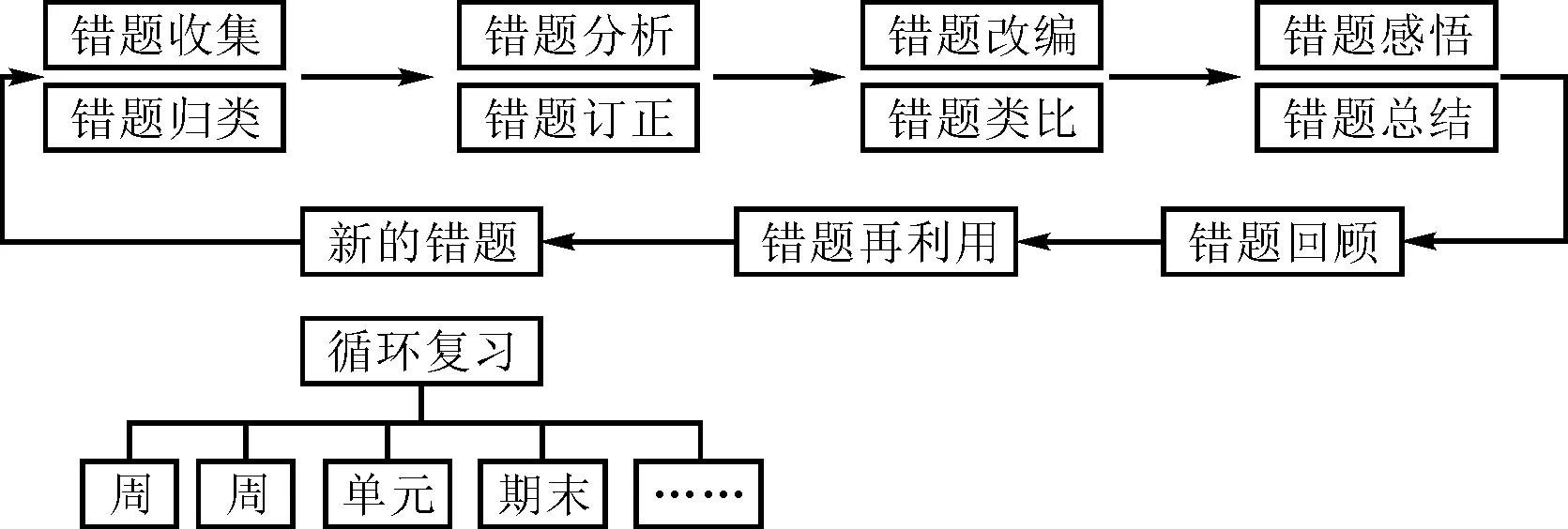
图1

3.1 错题收集、归类

错题的收集、归类，是错题管理的基础，往往没引起学生的重视．错题的收集、归类面对的问题是：收集怎样的错题，怎么收集？并不是所有的错题都得收集，应收集些典型的、有代表性的错题，且不是简单的堆积，而应进行整理、归类，使其系统化．建议可按以下标准分类：按书本目录——属于哪一章，哪一节；按题型——选择题、填空题、解答题；按知识点分类——函数、三角、数列、立几、解几等；按思维方法分类——概念、公式、定理、法则等；按渗透的核心素养分类——数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析．同一个错题，按不同的分类标准，可归于不同的类别，要求学生做目录，方便查找与使用，且方便进行二次错题管理．

3.2 错题分析、订正

错题分析、订正，是错题管理的重点，不是简单的照搬标准答案，旨在要指导学生分析错因，找准致错的症结，记录错题的切入点、思路的突破口，解题的技巧、解题步骤及小结等．并注释、写出自己解题时的思维过程，暴露出自己思维障碍产生的原因及根源的分析[2]．

3.3 错题改编、类比

错题改编、类比，是错题管理的难点，初始时往往需要教师的有效引导．教师可尝试改变错题的条件或结论，对错题进行改编，并寻找解决方案，触类旁通，举一反三，使知识系统化、思维娴熟化，真正提升核心素养．

3.4 错题感悟、总结

错题感悟、总结是错题管理的归纳总结环节，是经历前面错题的分析、订正、改编、类比后的感悟与收获．总结对错题的反思，可由具体题目出发，由点到面，总结一类题型；也可从思想方法上进行感悟，总结思想方法的运用；还可从解题方法上进行感悟，对解题方法进行总结，等等．

3.5 错题回顾、再利用

错题回顾、再利用，旨在对收集的错题经常性地进行回看、翻阅、消化，有计划地整理错题，并以现有的知识和能力对错题进行审视、分析，掌握运用.将已理解的、已掌握的错题标上记号，不清楚过段时间再分析．结合后续学习中新的错题，让一些错题再利用，形成动态系统[3]．

4 高中数学错题管理举例

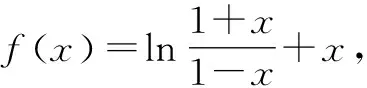
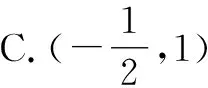
错题归类：函数、奇偶性、不等式、求范围、数形结合、直观与想象.

错题分析：

(2)对“数与式”的感知意识不够，捕捉不了函数及不等式背后蕴含的特征，不懂从函数的奇偶性着手．

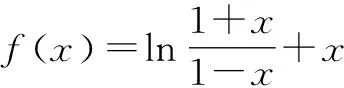
错题订正：

解析1：利用函数性质.

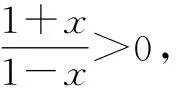
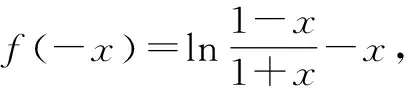
单调性：f(x)=ln(1+x)-ln(1-x)+x，可知f(x)在(-1,1)上为增函数．

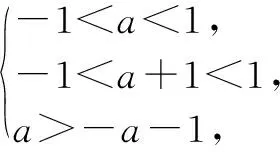
解析2：特值法.

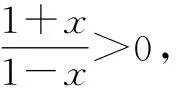
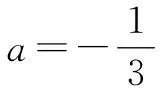
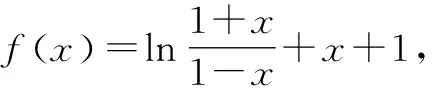
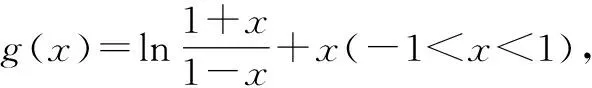
错题类比：

解析1:转化为奇函数.

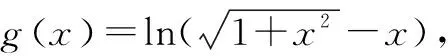
即g(a)+g(-a)=0.

所以f(a)+f(-a)=2.所以f(-a)=-2.

解析2:利用对称性.

由f(x)的对称中心为(0,1)⟺f(a)+f(-a)=2.

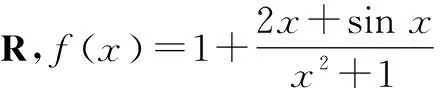
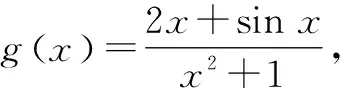
因为f(x)=1+g(x)的对称中心为(0,1).

所以M+N=2.

错题总结：

(1)对于函数，要有善于捕捉函数性质(奇偶性、单调性、周期性等)的意识；

(2)f(x)关于点(a,b)对称⟺f(a-x)+f(x+a)=2b.

5 结语

基于核心素养的高中数学错题管理，尝试以数学核心素养为视角，以错题管理为研究对象，充分利用错题收集、归类、分析、订正、改编、类比、感悟、总结、回顾、再利用等环节，探索科学的、积极的、主动的、渗透核心素养的错题管理方式，有一定的操作性及推广性．