巧用极化恒等式 妙解动态几何题

⦿重庆市忠县中学校

张 侣

⦿重庆市忠县中学校

胡江丽

平面向量是高中数学的基本内容，具有鲜明的独特性质(代数与几何的纽带)，现已成为人们研究的重点对象. 文献[1]表明极化恒等式建立了数量积与几何长度(数量)之间的联系，作为代数与几何的桥梁，具有化动(动点)为定(定点)、化动(动态)为静(静态)、化曲(曲线)为直(直线)、化普通为特殊之功效，应用十分灵活. 文献[2]也举例讨论了极化恒等式在部分解题中的应用.文献[3]以近几年高考试题、江苏省市级统考试题为例，对极化恒等式在数量积问题中的应用进行归纳剖析，探索其解题规律. 涉及动态几何中向量数量积的问题，运用常规方法很难找到求解问题的突破口，因而借助极化恒等式来求解就显得尤为重要.

1 极化恒等式的展示

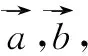
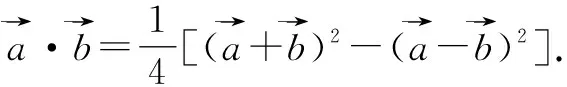
上式表明向量的数量积可以由向量的和、差运算的模来表示，该式将向量的数量积运算和向量的线性运算联系在一起，将不可度量的向量数量积关系转化为可度量、可计算的数量关系.

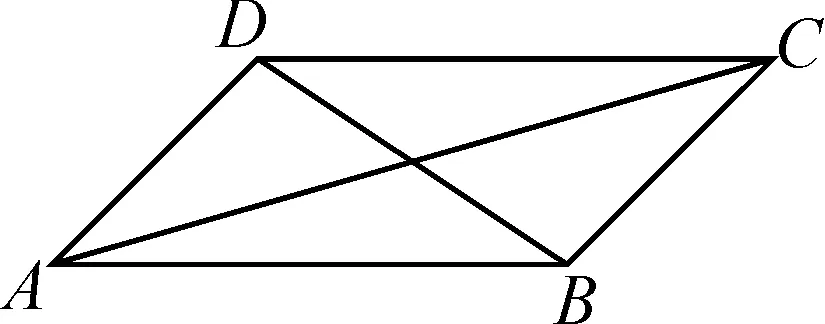
图1

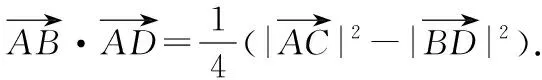
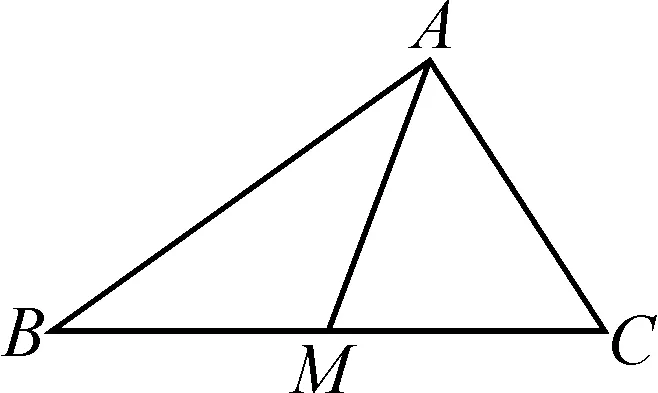
图2

推论2(极化恒等式的三角形模式)如图2，在ΔABC中，若M是BC的中点，则有

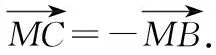
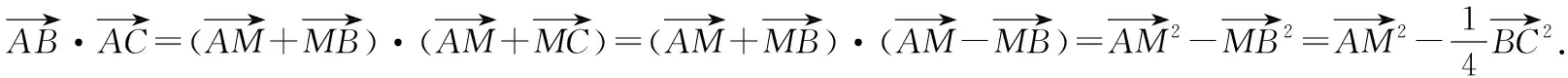
故得证.

2 极化恒等式的妙用

2.1 在平面几何中的妙用

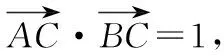
A.圆 B.椭圆 C.抛物线 D. 直线

分析：此题是通过给出平面的两个定点和向量数量积，求解动点的轨迹问题.问题设置简单，但考生很难快速解答，原因是虽然看起来破解此题的方法很多，有定义法、坐标运算等，但都涉及到大量的运算，不免给学生计算带来困难.若能借助平面向量的极化恒等式破解，则可事半功倍.

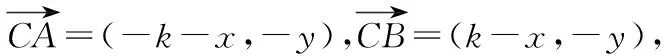
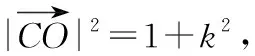
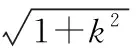
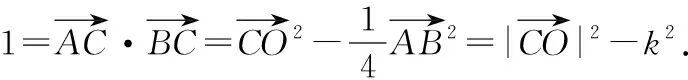
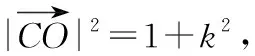
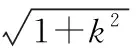
点评：此类问题的破解，因涉及思考方向不同，所获得求解方法也不同. 定义法和坐标法虽然容易想到，但难免出现大量的计算，容易造成计算错误. 而借助极化恒等式和圆的定义，问题的突破水到渠成. 根据问题的破解过程，可将原问题进行拓展，获得一般性结论.

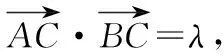
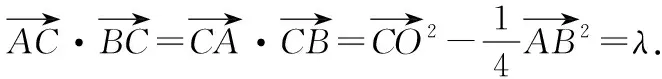
2.2 在立体几何中的妙用

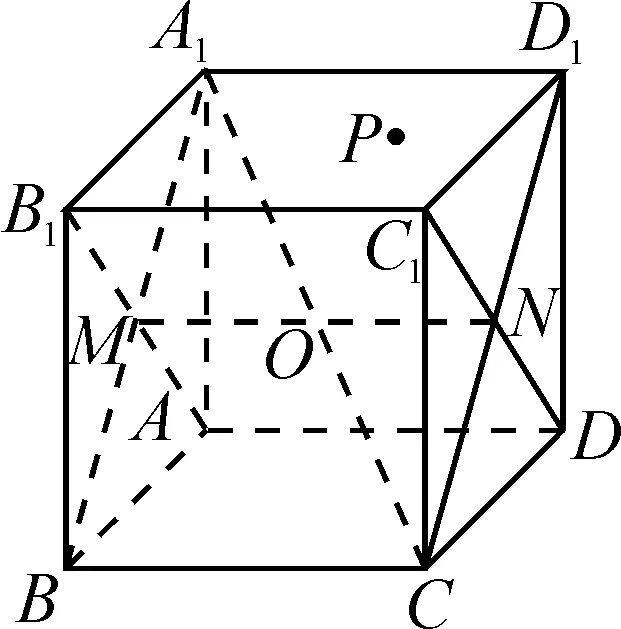
图3

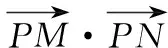
解法1：(一般解法)由题设知，当弦MN取到最长时，即MN为正方体ABCD-A1B1C1D1的内切球直径.

不妨设M,N为内切球与正方体在平面ABB1A1和平面CDD1C1的切点，易知点M,N分别为平面ABB1A1和平面CDD1C1的中心.

如图3，现以点A为坐标原点，以AB,AD,AA1所在的直线分别为x轴，y轴，z轴建立空间直角坐标系.

已知正方体ABCD-A1B1C1D1的棱长为2，则M(1,0,1),N(1,2,1)，设P(x,y,z)，此时

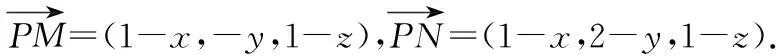
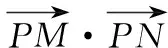
解法2：(极化恒等式)如图3，设球心为O，由题设知，当弦MN取到最长时，MN=2.

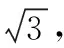
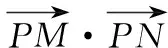
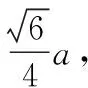
设外接球的球心为O，由极化恒等式得

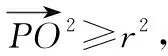
点评：以上两题都以正多面体为载体，结合球面上的两动点和正多面体上的动点，设置平面向量数量积问题.因问题中涉及多个动点，若按一般方法来处理很困难，但我们注意到此题中不管弦MN如何运动，球的直径始终为定值，由此借助极化恒等式，将多个动点转化为一个动点，使问题变得容易化解.

2.3 在解析几何中的妙用

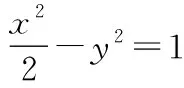
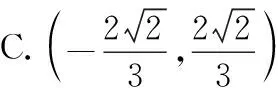
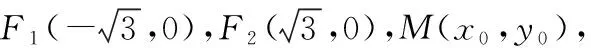
①

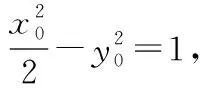
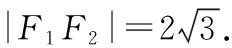
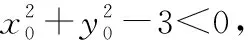
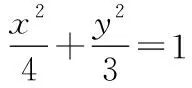
解法1：(一般解法)根据题意，设动点P(x0,y0)，A(x1,y1),B(-x1,-y1)，则

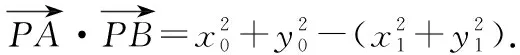
由于点P在抛物线上，点A,B在椭圆上，所以有

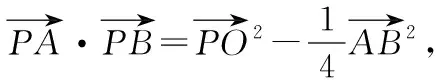
点评：在圆锥曲线中涉及向量数量积问题求解时，需结合问题本身的规律特点，合理处理向量关系，若采用一般方法破解，会涉及到方程消元，结合韦达定理将向量的数量积转化为坐标运算，此方法运算量一般都比较大，需要考生有扎实的运算能力. 若能巧妙地运用极化恒等式，可以减少运算，问题得以快速有效破解.

3 应用反思

本文研究用极化恒等式破解动态几何中的数量积问题，若用常用的方法(基底法，坐标法，几何意义法)有时在求解过程由于运算复杂会导致错误；若能根据图形特征，巧妙地运用极化恒等式进行思考与探究，很快就能找到问题的突破口. 这并不是追求高难度的解题技巧，而是想阐明极化恒等式也是处理向量数量积的一种常见思路. 向量是连接代数与几何的桥梁，由于向量中引入了坐标运算，使向量与代数运算密切相关，而几何运算就略显单薄，极化恒等式恰恰弥补了这个遗憾.极化恒等式把向量的数量积问题用形象的几何图形展示得完美无缺，实现了向量与几何、代数三者的有机结合，有利于培养学生的逻辑推理、直观想象能力和数学建模等素养.