一道高中数学会考题蕴含的多种解法与分析

夏顺友，仲崇轶，王常春，陈治友

（1.贵州师范学院 数学与大数据学院，贵州 贵阳 550018；2.遵义师范学院 数学学院，贵州 遵义 563006；3.贵阳学院 数学与信息科学学院，贵州 贵阳 550005）

贵州省2021 年12 月第43 题是以解析几何中圆为背景的最优化问题。题目如下：

已知圆O:x2+y2=r2(r＞0)过点。

（1）求圆O的方程；

（2）已知点A(-40)，，B(2,0) 点M是圆O上任意一点，求的最大值，并求出此时点M的坐标。

该题蕴含了一类线性目标函数在二次约束条件下的最大值问题。

该题第一问略去分析，针对第二问蕴含的类似问题以及一般问题的多种解法进行陈述并解析，再对题目蕴含的一般二次约束条件下的线性目标函数的最大值问题的多种一般解法进行论述。

1 多种解法与分析

本节不针对原题进行多种解法陈述与分析，只对下面类似问题进行。

已知圆O:x2＋y2=4上任意一点M，和点A(-2，0)，B(4，0)，求的最大值，并求出此时点M的坐标。

设M的坐标为(x,y)，则x2＋y2=4，则

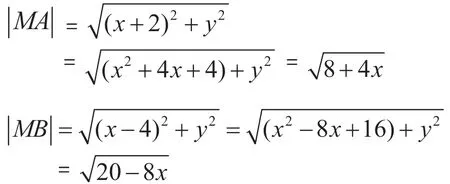
解法一：利用均值不等式求解

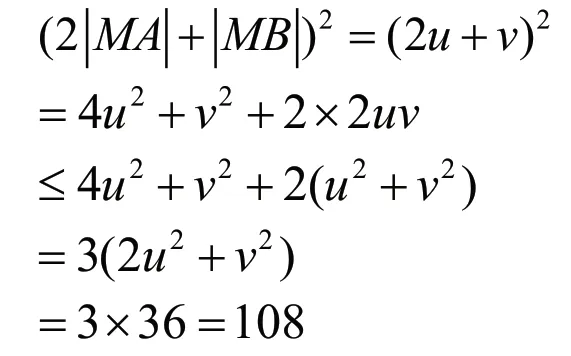
20-8x=12，8+4x=12

由此得x=1代入x2+y2=4得y=。

注1.1 均值不等式主要对“等积问题”、“等周问题”，即“n个正数的乘积为常数，则当它们相等时它们的和有最小值”“n个正数的和为常数，则当它们相等时它们的乘积有最大值”。该题所使用的方法和针对的问题有较好技巧。下面给出一个较一般例子与做法。

求约束条件 6u2+4v2＝25下z=3u+2v的最大值。

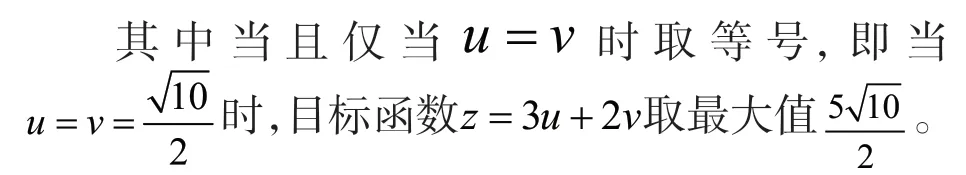
解法二：化为一元函数最值求解

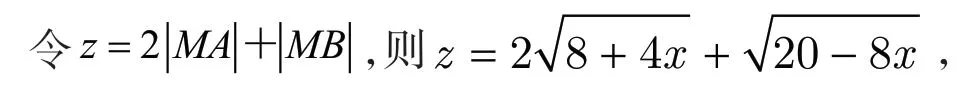
其中－2≤x≤2，z是x的函数，为求z的最大值，先求z对x的一阶导数

解法三：拉格朗日乘数法

拉格朗日函数为：

注1。2 作为 2u2+v2=36约束下对二元目标函数f(u,v)=2u＋v最大值求解通用方法就是拉格朗日乘数法。如果不整体代换，直接对下述问题：

约束条件x2＋y2=4下，求解目标函数

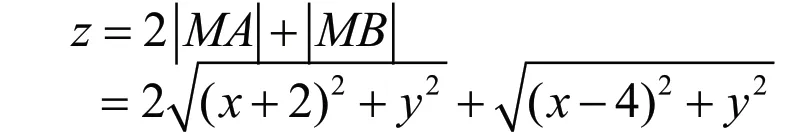
的最大值，也可以直接利用拉格朗日乘数法，此处不做求解。

解法四：判别式法求解

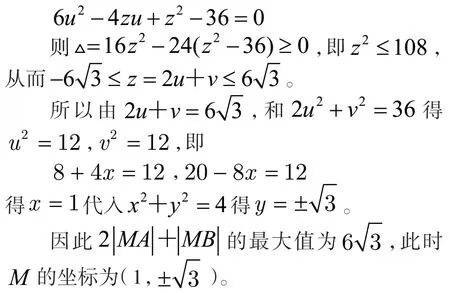
解法五：凸规划结合判别式求解

注1.3 解法四和解法五都用判别式法，但是解法四是利用有解做，而解法五是利用凸规划思想，再利用几何意义的相切而做。

解法六：利用三元柯西不等式求解

解法七：利用二元柯西不等式求解

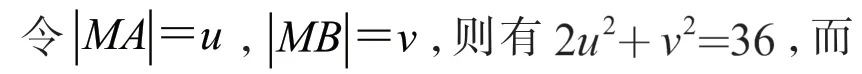
解法八：参数换元结合三角函数求解

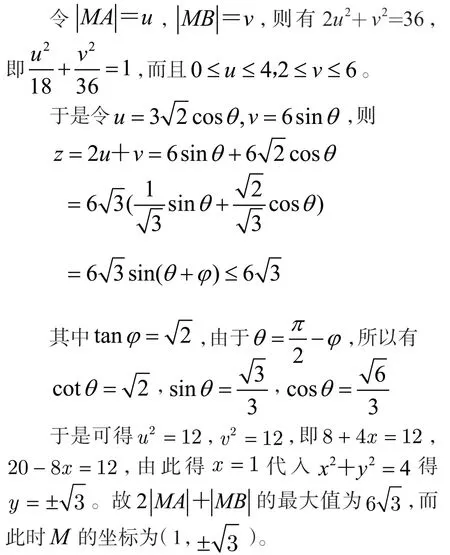
注1.5 该解法先代换一次，再利用参数方程化为三角函数求解，问题变得简化。如果不做第一次代换，直接对问题：

约束条件x2＋y2=4下，求解目标函数

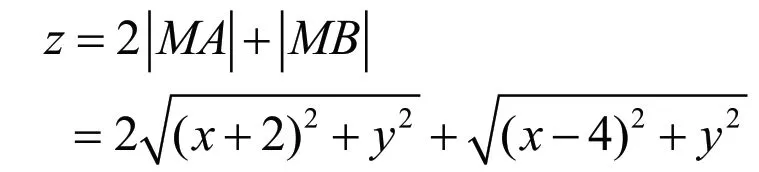
的最大值。

令x=2cosθ,y=2sinθ把目标函数转化为三角函数求解也可以，会复杂得多。

解法九：化为一元函数最值求解

注1.6 该方法与解法二有一些不同之处。解法二在原问题上进行，而解法九是做代换后做。

解法十：梯度法求解

注1.7 梯度反映了多元函数值递增最快的方向。因为目标函数是二元线性函数是平面，约束是椭圆柱面，它们的交线是封闭的椭圆。显然有最高点和最低点，对应相应的最大值与最小值。

2 一般问题与解法

本节对原题所蕴含的更一般的多元线性目标函数在二次约束条件下的最大值问题模型和求解方法进行阐述。

一般数学模型：

其中b＞0，a1≠0,a2≠0,...,an≠0，且

b1＞0,b2＞0,...,bn＞0

该模型求解的方法一是拉格朗日乘数法，其次是柯西不等式方法，再是利用均值不等式方法。

3 会考情况与解题教学实践情况

该会考题两问，每问5 分，参加人数70064，本题平均得分在包含零分卷时是3.45 分，如果不包含零分卷，则平均得分是5.19 分，这说明考生们基本上都掌握了圆的标准方程的初步知识，但对圆外两点与圆上一点的距离之和取最大值的求法掌握得普遍差一些。得分情况见下表：

该题在数学与应用数学专业本科生解题教学训练课程中有很好的培养学生的创新思维能力（见［6］）。另外文献［4］和文献［5］中的题也可以增加本文中的梯度法和拉格朗日乘数法，此处不再详述。