基于空间自相关模型的农业经济演化分析

吴 笛

（大连财经学院，辽宁 大连 116622）

我国以农立国，农业发展与人民生活水平直接相关，在国家经济增长中占据了重要位置。随着我国经济进入新常态，要实现经济的持续增长，提高低收入人群的经济能力有着重要意义，因此提高农业经济增长是这一阶段的重要任务［1］。然而农业经济增长不仅有关经济学问题，同时会受到复杂的自然环境影响，以及地理环境因素限制。当前对农业经济增长的影响因素分析多是集中在实物投入、技术变量、制度变量等方面，少有涉及农业经济发展的地理因素分析［2］。空间计量经济学在当前被应用于众多经济增长研究中，其利用地理相关性分析提高了经济分析的垂直深度，对于区域经济政策制定有着直接帮助［3］。本文利用空间分析工具，探索农业发展和经济增长在地理空间上的演化规律。

1 基于空间自相关的农业经济演化分析

1.1 农业经济视角下的空间自相关

在地理空间中，事物之间必然存在着关联性，越邻近的事物关联越紧密。空间自相关是对探索性空间数据进行临近效应分析，从而发掘其在空间全局或局部上的分布特性［4］。以图1 为例，它以简单图形对空间自相关进行了描述。（a）为正空间自相关，即在确定区域内，随距离缩小，研究对象的相似特性明显聚集；（b）为负空间自相关，即在确定区域内，随距离缩小，研究对象的相异特性明显聚集。在空间自相关程度高的区域，相邻空间单元的SAA 大，不相邻空间单元的SAA 小，则是正空间自相关；反之则是负空间自相关。进一步来看，在研究区域内，研究对象的特征集聚说明空间自相关程度高；反之则空间自相关度低。

图1 空间自相关示意图

空间权矩阵（Spatial Weight Matrix，SWM）是描述事物关联程度的工具，它包括邻接矩阵和距离矩阵两种类型［5］。邻接矩阵的依据是事物的空间相邻关系，如图2 所示。在图2 中，（a）表示共点连接，即空间单元A 与B 有共用点；（b）表示共边连接，即空间单元A 与B 有共用边；（c）表示共边点连接，即空间单元A 与B 有共用点和共用边。

图2 三种空间相邻关系

设地区i,j，且研究区域内共n个地区。对二元对称空间权重矩阵作下式定义，其中WT=W。

对W*进行行标准化操作，并得到邻接矩阵W，其中wij=。

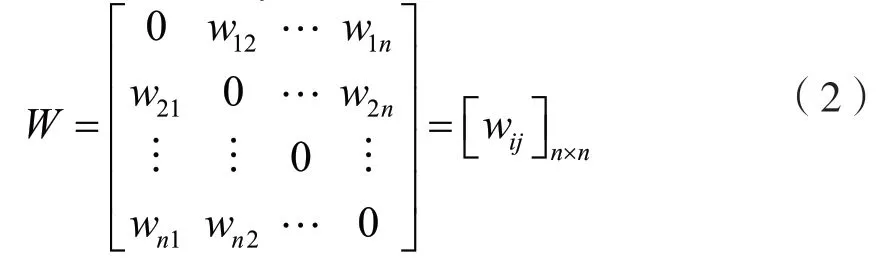
距离矩阵则是通过空间单元中心之间的欧几里得直线距离描述空间相邻关系，这里不再赘述。

1.2 空间自相关的测度方法

对事物的空间自相关性进行判断时，需要用到以下几种方法。全局Moran’s I 能反映空间整体的分布情况，局部Moran’s I 则反映了局部空间的分布情况［6］。设地区i,j,k,h∈n；用S0表示空间权重矩阵的元素和；xi和平均值分别表示观测值和所有观测值的均值，全局Moran’s I 和局部Moran’s I 的计算公式如下。

若I＞0，则正空间自相关；若I＜0，则负空间自相关；若I=0，则空间不相关。对空间权重矩阵进行行标准化处理后，I∈[-1,1]。由此可知，I值趋于-1 或1，是研究对象区域集聚的表现，空间自相关程度高；I值趋于 -1/(n-1)，是研究对象在区域随机分布的表现，空间自相关程度低［7］。局部莫兰指数与全局莫兰指数类似。

检验空间分布的随机性，需要统计量P 值和Z 得分。Z 得分（Z-scores）反映了数据集的离散程度，P 值（Probability-Value，Pr）则反映了空间分布的发生概率［8］。设零假设H0：空间总体随机分布。零假设是否接受，可以判断空间是否具有相关性。公式（4）为Z 得分式。

当检验对象为全局或局部空间时，有下述关系存在，其中N 和R 分别表示正态条件和随机条件。

正态或随机条件下，全局Moran’s I 的方差计算式如下。

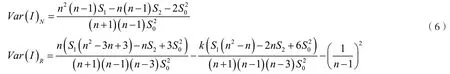
相应地，局部Moran’s I 的方差计算式如公式（7）:

所有局部Moran’s I 的均值即全局Moran’s I。图3 为Moran’s I 空间自相关四象限图。设显著性水平为α。正空间自相关对应结果为Z(I)＞Zα/2；负空间自相关对应结果为Z(I)＜-Zα/2；空间不相关对应结果为 -Zα/2≤Z(I)≤Zα/2［9］。局部检验与之类似。在局部检验且空间呈正相关性时，若相邻空间单元的Moran’s I 均很高，则为热点（Hot Spots），用High-High 表示；若相邻空间单元的Moran’s I 均很低，则为冷点（Cold Spots），用Low-Low 表示。在局部检验且空间呈负相关性时，即Z(Ii)＜-Zα/2，此时邻接的空间单元观测值出现较大差异，用High-Low 或Low-High 表示。正相关性反映了空间扩散效应，负相关性则反映了空间互斥效应。

图3 Moran’s I 空间自相关四象限图

上述检验方式仅能从Moran’s I 角度进行检验，为测度局部空间冷点区和热点区的分布，本研究还结合了局部关联指数Getis-Ord’s Gi*进行分析，其计算公式如下所示［10］。

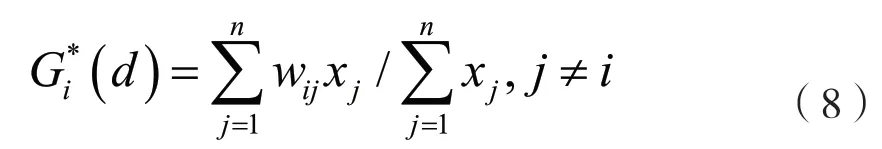
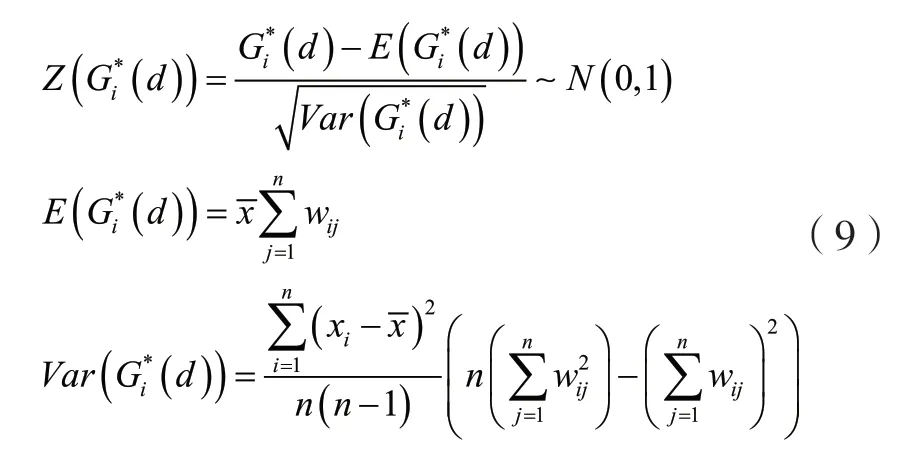
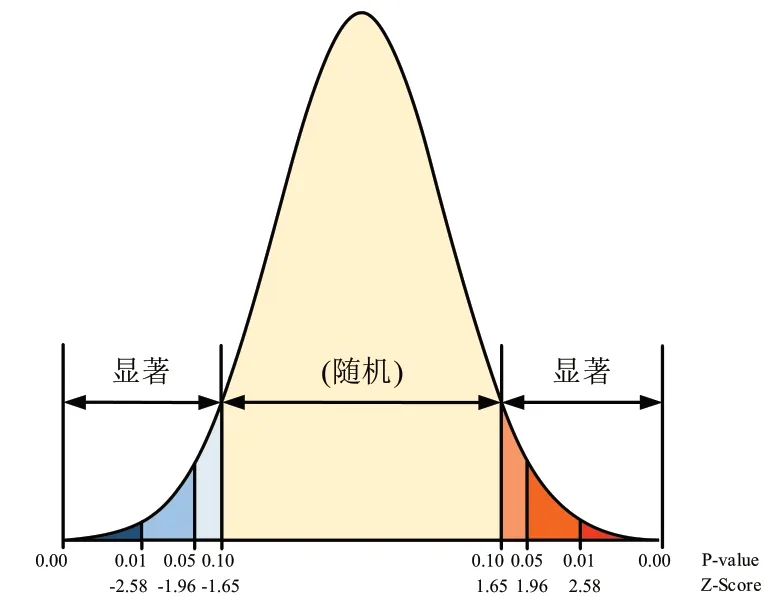
图4 P 值和Z 得分的关系

1.3 农业经济计量的空间自回归模型构建

经济问题通常运用计量回归模型进行分析，若将空间相关性纳入模型中，则可以空间自回归模型解决问题。图5 对空间误差模型和空间滞后模型进行了形象表述。ε是随机误差项，空间误差模型是将区域局部特征之间的随机误差纳入考虑，空间滞后模型则是将误差考虑到研究区域的内生交互作用中。

图5 空间误差模型（A）和空间滞后模型（B）

先提出无空间效应的空间个体面板数据模型，其数学表达式如下：

对被解释变量yit，在时间维度t上，µ为空间个体效应，影响它的解释变量为Xit。对农业经济而言，将第一产业增值作为被解释变量，则影响它的解释变量有多种。

以式（10）为基础，设解释变量为农业机械总动力xa，乡村从业人员xb，农用化肥施用量xc，农作物播种面积dx，平均气温变化xe，降雨量变化xf。

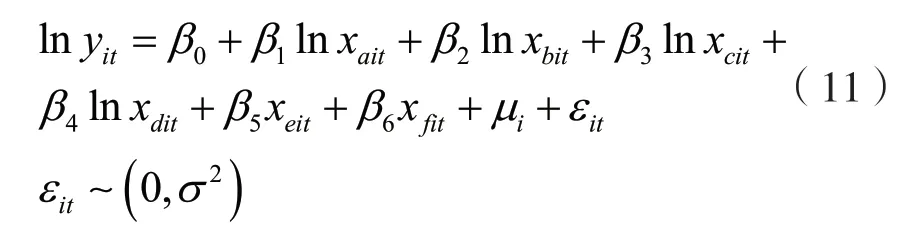
在式（11）中，平均气温和降水量变化存在负值情况，因此不取对数。在农业发展中，施用化肥是一面双刃剑，因此将化肥过度施用量xg考虑在内，并得到下述模型。

在考虑气温对农业的影响时，本研究由最高气温Tmax、最低气温Tmin、平均气温Tmean构造了如下指标，以衡量气温变化。

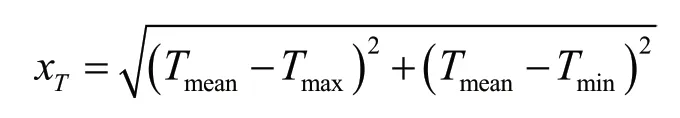
同时，为了反映降雨量变化对农业经济的影响，这里提出了降雨量变化指标。

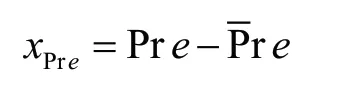
采用优化后的气温及降雨量变化指标对式（12）进行改进，得到下述方程。

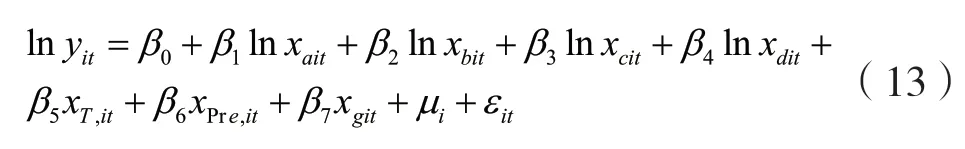
以2010-2018 年我国的农业经济增长数据为例，对式（11）、（12）、（13）进行检验，统计量通过0.01 的显著性水平检验，因此采用固定效应的空间面板杜宾模型。空间杜宾模型如下所示。

从式（14）可以看出空间杜宾模型反映了三层含义，第一层是被解释变量在其局部空间与相邻空间存在自相关性;第二层是局部空间的被解释变量与自变量互为相关;第三层是局部空间被解释变量与相邻空间自变量存在自相关性。

2 基于空间相关性模型的我国农业经济演化实证分析

2.1 基于全局Moran’s I 的我国农业经济空间演化分析

判断农业经济在研究地区的空间自相关性，是探讨其空间演化规律的基础。以2018 年的农业经济情况为例，对我国第一产业增加值进行探索性空间数据分析，研究其是否存在空间聚集现象。图6 为我国农业经济的空间分布图，（a）为第一产业增加值对数形式的数据分析结果；（b）为农业经济局部关联指数的分析结果。在图6（a）中，以Jenks 自然断开法将第一产业增值分为八种类型，并用不同颜色示意。从图中可以看出，我国西部地区和中北部地区均属于第一产业产值较弱的地区；在我国中东部地区，第一产业的产值明显较高；整体看来，低产值区和高产值区出现空间集聚现象。

图6 我国农业经济的空间分布

在图6（b）中，局部关联指数Getis-Ord’s G 能够更为准确地判断局部地区农业经济的聚集情况。西部地区表现出显著低值聚集，东部沿海地区呈现出明显的高值聚集；除此之外，在-1.64～1.65 这一区间，农业经济发展无显著的空间集聚现象，这一情况在中东部区域存在。整体看来，Getis-Ord’s G 的判断结果与Moran’s I基本一致。从上述结果分析来看，第一产业增加值的对数形式表现出空间集聚现象，但其未能反映出农业经济的空间聚集类型。接下来将采用Geoda1.4.0 各地区数据进行全局自相关分析，分析结果如图7 所示，其中（a）为全局Moran’s I 指数的四象限图，（b）为全局Moran’s I 的置换检验。

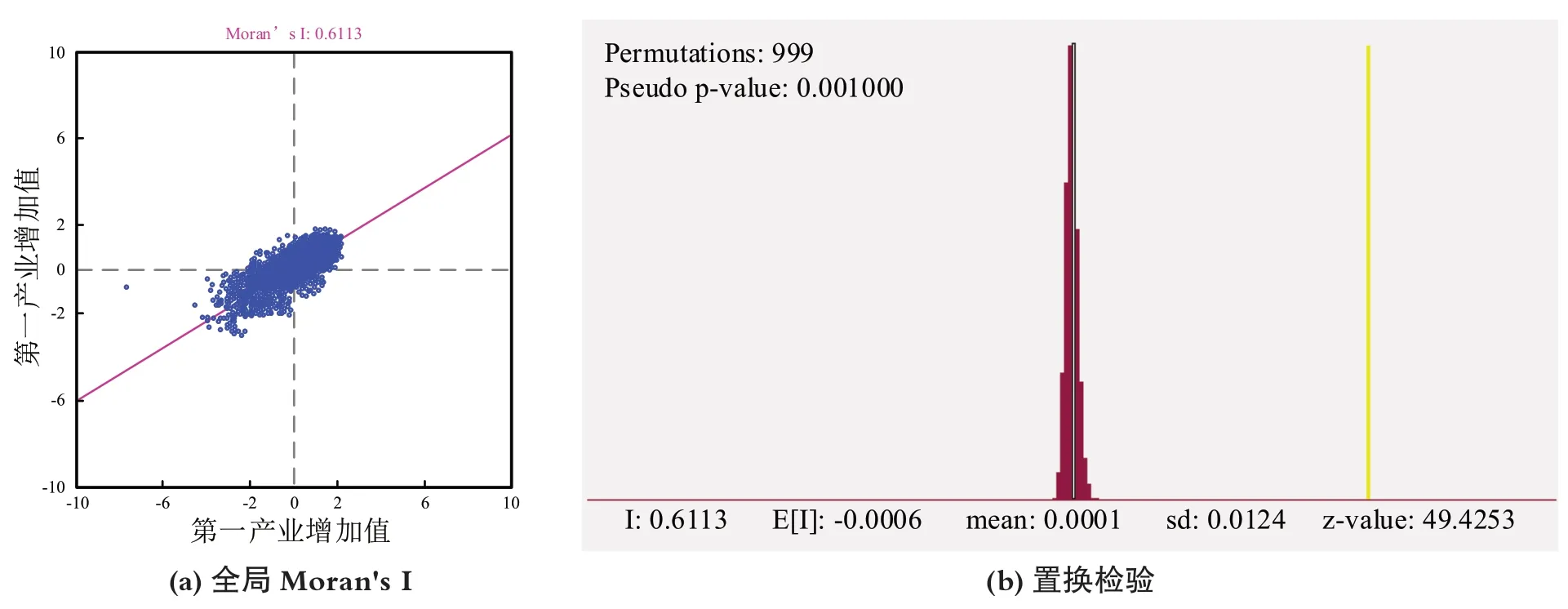
图7 我国农业经济的全局Moran’s I 指数

图7 结果显示，点在第一、三象限集中分布，处于这两个象限的点表现为空间正自相关性；全局Moran’s I 值为0.6113，P 值结果通过了0.01的显著性水平检验，这说明空间分布非随机现象。由此可知，我国农业经济在99.9%的置信度下，存在显著的正空间自相关性，农业经济的相似特征集聚。

2.2 基于H 省农业经济的局部空间演化分析

以H 省为例，对其农业经济数据进行分析。图8 为H 省的局部Moran’s I 散点图，其中（a）为2010 年的数据，（b）为2018 年的数据。从图8中各地区农业经济情况的空间分布来看，位于第一、三象限的地区分别为High-High 分布和Low-Low 分布，它们与相邻地区的农业经济情况为正空间自相关；位于第二、四象限的地区分别为Low-High 分布和High-Low 分布，它们与相邻地区的农业经济情况为负空间自相关；与2010 年相比，2018 年H 省各地区的农业经济情况呈现出更为显著的空间效应。

图9 为H 省农业经济的LISA 图形，其中（a）为2010 年的数据，（b）为2018 年的数据。从图中可以发现，H 省的High-High 热点区较多，呈现出“U”形空间形态，分布在H 省南部；H 省的Low-Low 冷点区较少，位于中部和北部；Low-High 区较多，且其稳定分布于H 省中部和北部；High-Low区仅一个，位于H 省西部。整体来看，从2010 年到2018 年，H 省的热点区和冷点区表现为增加、聚集两种趋势，热点区的“U”形空间形态呈现为收拢形势，冷点区数量增加。这说明H 省的农业经济空间效应趋于稳定，空间关系逐渐成熟。这一结果与图8 的分析结果基本一致。

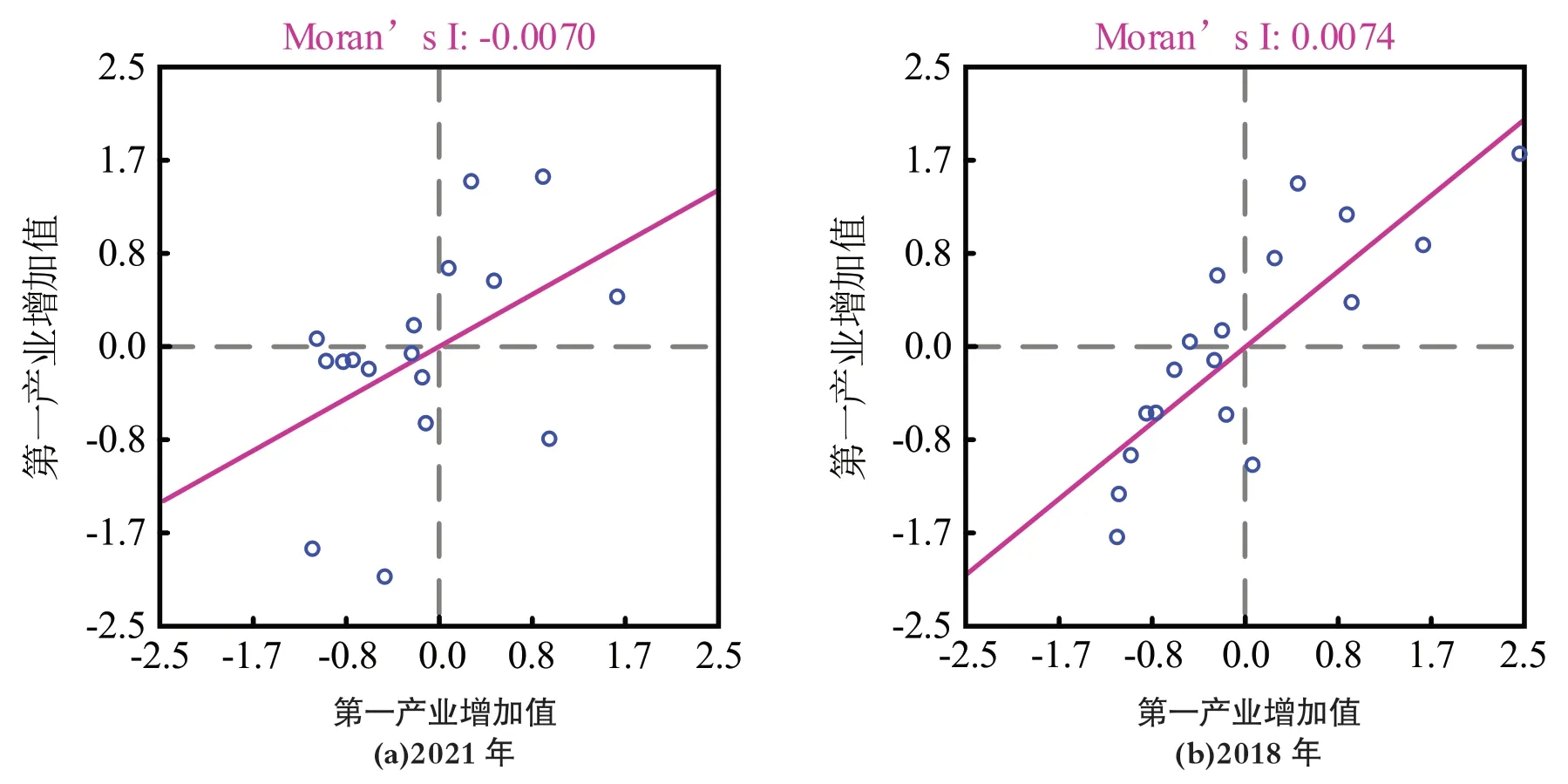
图8 H 省农业经济的局部Moran’s I 散点图

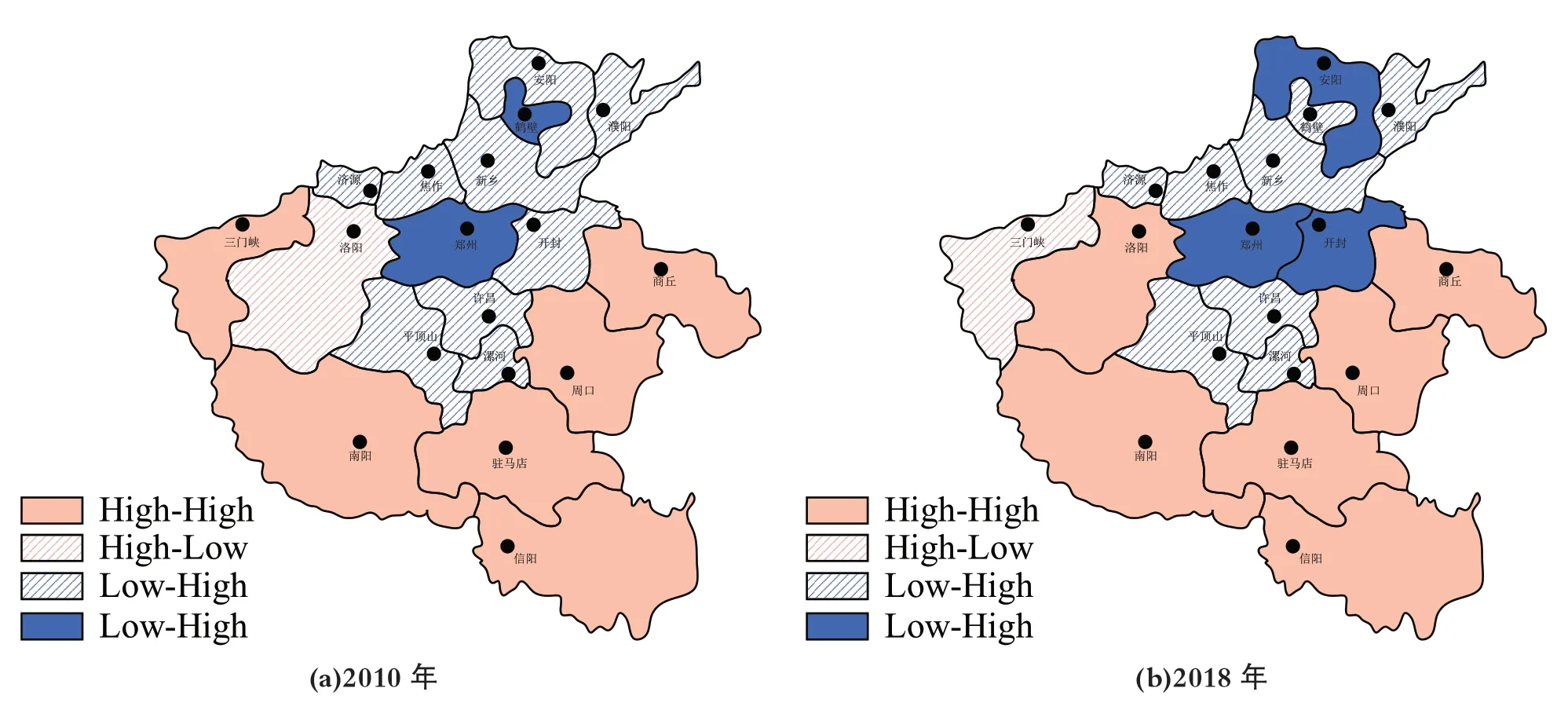
图9 H 省农业经济的LISA 图形

综上所述，我国农业经济发展情况呈现出显著的空间集聚现象。从全局来看，农业经济的空间演化表现为东部地区高值聚集、西部和中北部地区低值聚集，且空间正自相关性显著。以H 省为例进行局部空间演化分析，H 省的农业经济热点区多分布于南部和东部，H 省中部和北部多呈现出负空间相关性，农业经济的空间格局逐渐稳定。将这两种结果进行联合分析，可以发现H 省农业经济的空间演化形势与我国农业经济的全局演化形势存在一定的差异性，这是由于H 省位于我国的中东部地区。另一方面，这也可以看出，我国农业经济在南北方向上呈现出南高北低的演化形势。

3 结论

为探索我国农业经济增长在地理空间上的演化规律，本研究采用空间自相关分析和空间自回归模型对农业经济增长数据进行处理，以实际数据进行了实证分析。研究结果显示，我国农业经济呈现出东部地区高值聚集、西部和中北部地区低值聚集的演化形势，第一产业的产值整体呈现出东高西低、南高北低的梯形趋势。以H 省为例进行局部空间演化分析，H 省南部呈现出正空间自相关性的“U”形高值聚集；H 省中部和北部表现为负空间自相关性；整体来看，H 省的农业经济空间格局表现出增加、聚集的趋势。本研究所提出的农业经济空间自相关模型表现出良好的分析效果，不仅为区域农业经济发展的政策制定提供了依据，而且为农业经济的多维度空间数据分析奠定了基础。