一道立体几何问题的多视角探究

汪 梅

(江苏省昆山市柏庐高级中学)

立体几何问题可以考查学生的空间想象能力、运算能力、识图能力.角度和距离是立体几何中两个重要的度量,其中线面角的概念和求法既是教学的重难点,也是高考的高频考点.学生在解决线面角问题时会面临两个选择:运用几何法(传统方法)求解或运用向量法求解.在运用几何法解题时学生常感到作图难,角不好找;在运用向量法解题时学生可能会遇到个别点的坐标不好求,从而导致解题失败.本文以一道立体几何题为载体,从几何法和坐标法这两种视角深刻分析这类题的解决方法.

1 试题呈现

题目如图1所示,在四面体ABCD中,已知△ABD是边长为2 的等边三角形,△BCD是以点C为直角顶点的等腰直角三角形,E为线段AB的中点,G为线段BD的中点,F为线段BD上的点.

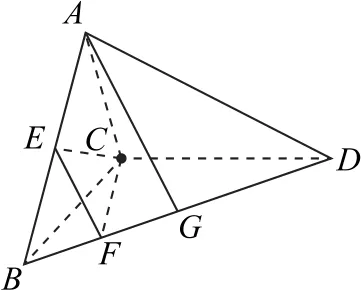
图1

(1)若AG∥平面CEF,求线段CF的长;

(2)若二面角A-BD-C的大小为30°,求CE与平面ABD所成角的大小.

2 解法探究

在第(1)问中,由线面平行的性质定理可得AG∥EF,从而得出F为BG的中点,进而可以在△BCD中求出CF.

在第(2)问中,首先要找出二面角A-BD-C的平面角,若用几何法求CE与平面ABD所成角的大小,需要作出线面角或用等积法求出C到平面ABD的距离,但是四面体ABCD的体积不易求出;若用坐标法求解,那么如何建系及求出点A的坐标是难点.

视角1几何法

分析1真作高真求高策略:运用射影法作出斜线在平面内的射影,进而将线面角转化为线线角,最终转化为求三角形中的角.先作出线面角,再在具体直角三角形中求解.

解法1如图2所示,连接CG,因为△BCD与△ABD是共用同一条底边BD的等腰三角形,且G为BD的中点,所以AG⊥BD,CG⊥BD.

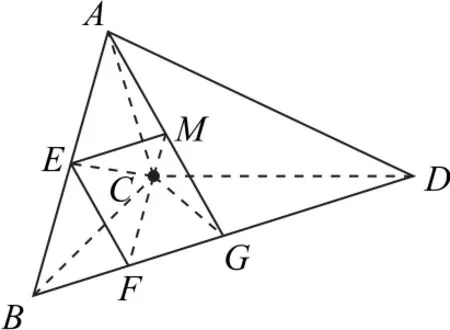
图2

又因为CG⊂平面BCD,AG⊂平面ABD,所以∠AGC为二面角A-BD-C的平面角,所以∠AGC＝30°,得AG＝,CG＝1,过点C作CM⊥AG,垂足为M,连接EM.

因为AG⊥BD,CG⊥BD,AG∩CG＝G,AG⊂平面ACG,CG⊂平面ACG,所以BD⊥平面ACG,因为CM⊂平面ACG,所以BD⊥CM.因为BD∩AG＝G,BD⊂平面ABD,AG⊂平面ABD,所以CM⊥平面ABD,所以ME为CE在平面ABD内的射影,故∠CEM为CE与平面ABD所成角.

点评本题属于中档题,注重对四基(基础知识、基本技能、基本思想、基本活动经验)的考查,体现了基础性、综合性、应用性、创新性的特点.几何法以逻辑推理作为工具解决问题.用几何法解题首先要掌握二面角平面角的作图方法,厘清图中面面、线面间的关系,分析出平面ACG和平面ABD的垂直关系是能否直接作出线面角的关键.

转换视角若作射影有难度,线面角不易直接求得,可运用等体积法间接求出点到平面的距离.

分析2假作高真求高策略:等体积法,求点到平面的距离(此时无须关注垂足的具体位置).

解法2同解法1可求得∠AGC＝30°.

点评有些学生对二面角平面角及线面角概念理解不到位,可能作不出二面角A-BD-C的平面角,更作不出线面角.视角2中很多学生想不到用转化法求三棱锥C-ABD的体积.新高考全国卷注重对立体几何中传统方法的考查,事实证明遇到立体几何问题就建立空间直角坐标系运用向量法求解不一定是最好的方法,所以多掌握一些解题方法是有益处的.方法单一,仅凭借一种方法应对所有的题目有时是吃亏的.对比以上两个视角,视角1利用面面垂直的性质直接作出了线面角,视角2利用等体积法求出点到平面的距离,但是视角1体现了数学中“多思少算”的理念,所以要求学生在平时的训练中优化自己的运算.

转换视角有时无论是直接作图还是运用等积法都不易求出高,此时可以考虑借助空间向量解决问题,因为向量是研究几何问题的有效工具.

视角2向量法

分析3直线与平面所成的角,可以转化为直线的方向向量与平面的法向量的夹角.若直线的方向向量与平面法向量夹角为锐角,则对应线面角是其余角;若两向量夹角为钝角,则线面角为其补角的余角.

解法3如图3 所示,连接CG.在等边△ABD中,G为BD的中点,所以AG⊥BD.又因为△BCD是以点C为直角顶点的等腰直角三角形,G为线段BD的中点,所以CG⊥BD,所以∠AGC为二面角A-BD-C的平面角,所以∠AGC＝30°.

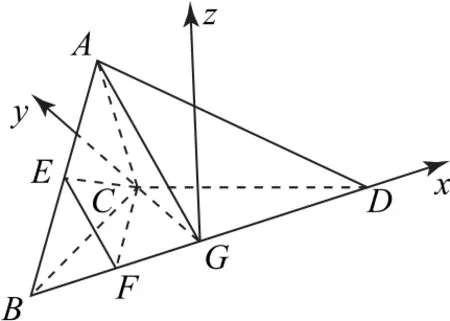
图3

又0°≤θ≤90°,所以θ＝45°,故CE与平面ABD所成角的大小为45°.

点评z轴的建立是本题的关键,笔者认为最好能找出底面的垂面,利用面面垂直的性质可知只要在垂面内作交线的垂线就可以作出z轴.不难发现,视角1中的几何法无疑是本题最简单的解法.

3 问题的拓展

变式在边长为2的菱形ABCD中,∠BAD＝60°,点E是边AB的中点(如图4),将△ADE沿DE折起到△A1DE的位置,连接A1B,A1C,得到四棱锥A1-BCDE(如图5).

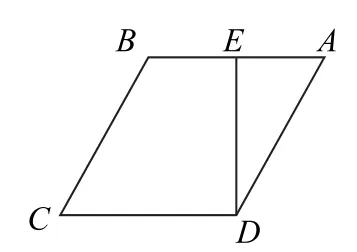
图4

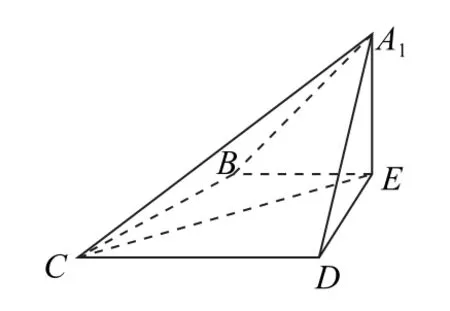
图5

(1)证明:平面A1BE⊥平面BCDE;

(2)若A1E⊥BE,连接CE,求直线CE与平面A1CD所成角的正弦值.

解析(1)证明过程略.

(2)方法1真作高真求高策略

如图6所示,易证CD⊥平面A1DE.因为CD⊂平面A1CD,所以平面A1CD⊥平面A1DE.

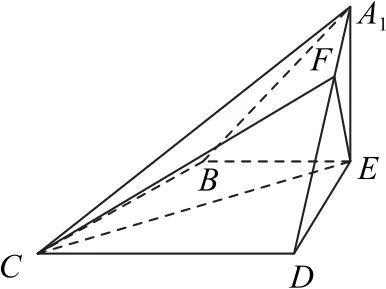
图6

因为平面A1CD∩平 面A1DE＝A1D,在△A1CD中,过E作EF⊥A1D于F,连接CF,则∠ECF是直线CE与平面A1CD所成角.

方法2假作高真求高策略

因为A1E⊥BE,A1E⊥DE,BE∩DE＝E,BE⊂平面BCDE,DE⊂平面BCDE,所以A1E⊥平面BCDE.因为CD⊂平面BCDE,所以A1E⊥CD,因 为CD⊥DE,DE∩A1E＝E,DE⊂平 面A1DE,A1E⊂平面A1DE,所以CD⊥平面A1DE.因为A1D⊂平面A1DE,所以CD⊥A1D,又因为CD＝A1D＝2,所以S△A1CD＝2.

方法3向量策略(建系法)

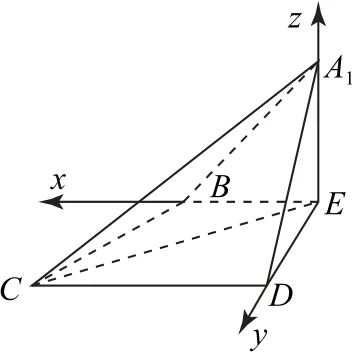
图7

设平面A1CD的一个法向量为n＝(x,y,z),则

4 解题反思

新高考注重对学生能力的考查,强调知识之间的关联与延伸,强调对学科关键能力尤其是对思维认知能力的考查.该类型题目对数学中逻辑推理能力、直观想象能力、数据分析与处理能力等均有涉及,注重对数学核心素养的考查.

立体几何中综合法求角关键是“找、作、化”,不论是找出所求角还是作出所求角,最后一定要归到一个可解的三角形中求解.

注重非特殊图形情况下建系训练,真正掌握运用空间向量的方法解决问题,而不是只会套路性地解题.运用空间向量法求解问题时,要避免建系不当或者是因为运算错误造成失分.

(完)