例谈一元二次方程的异化与同构在初高中数学中的运用

俞 纲 张文俊 李毅梅

(云南省昆明市第三中学)

解方程是学生在初中就学习过的内容,但很多时候,我们对方程的使用只注重如何根据方程的标准形式求出方程的根,而忽视对方程结构的灵活运用.纵观近年的中考和高考试题,有不少题都需要通过对方程结构的灵活运用来寻找计算的突破口,这值得学生重视.

1 方程结构的异化使用

例1(2021年云南中考卷24)已知抛物线y＝－2x2＋bx＋c经过点(0,－2),当x＜－4时,y随x的增大而增大,当x＞－4时,y随x的增大而减小.设r是抛物线y＝－2x2＋bx＋c与x轴的交点(交点也称公共点)的横坐标,m＝

(1)求b,c的值;

(2)求证:r4－2r2＋1＝60r2;

(3)以下结论:m＜1,m＝1,m＞1,你认为哪个正确? 请证明你认为正确的那个结论.

解析(1)b＝－16,c＝－2(求解过程略).

(2)由于方程r2＋8r＋1＝0的根比较复杂,且r不指定是哪一个根,因此不能简单运用求根公式或根与系数的关系直接解决,要将方程有针对性地“异”化为其他形式进行求解.

点评上述两题难倒很多学生,大家想不到要将标准的一元二次方程异化为其他形式进行求解,因此“吐槽”此题很偏很怪,完全不是一元二次方程的典型问题,甚至很多高中学生都无从下手.其实这些题并不是很难,只是学生对于方程的使用过于机械与死板,缺乏对方程的结构与形式进行有针对性的变形,缺乏灵活运用的意识.其实这种意识在高中也是必须具备的,如函数中的隐零点问题就是这种思想的运用.当然,除了要注意把一个方程异化为其他形式之外,我们还要注意能在多个形式类似的方程中发现其共同的结构本质,从而同构出相同的方程.

2 方程结构的同构使用

(1)求椭圆C的标准方程;

(2)若动点P(x0,y0)为椭圆外一点,且点P到椭圆C的两条切线相互垂直,求点P的轨迹方程.

当过点P的两条切线均与坐标轴垂直时,P的坐标为(±3,±2),此时点P也在圆x2＋y2＝13上.

综上,点P的轨迹方程为x2＋y2＝13.

点评求解该题的技巧在于两条切线所满足的条件是相同的,从而两切线斜率所满足的等式是相同的结构,从而同构出一个一元二次方程,并运用根与系数的关系来转化,避免了复杂的计算.

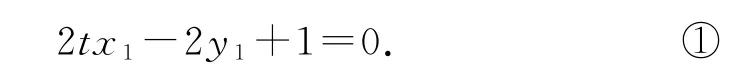
同理,切线DB的方程为

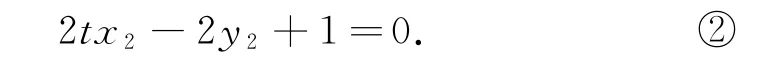
把式①与式②分别看作关于x1,y1和x2,y2的二元一次方程,它们结构相同,我们同构得2tx－2y＋1＝0,则A(x1,y1),B(x2,y2)都满足该二元一次方程,而两个不同点确定唯一一条直线,所以直线AB方程为2tx－2y＋1＝0,直线AB恒过定点

点评求解该题的技巧在于并没有用A,B两点坐标来表示直线AB的方程,而是从直线DA的方程和直线DB的方程同构出一个二元一次方程,以此作为直线AB的方程,避免了复杂的计算.

例5(2021年全国甲卷理20)抛物线C的顶点为坐标原点O.焦点在x轴上,直线l:x＝1 交C于P,Q两点,且OP⊥OQ.已知点M(2,0),且圆M与l相切.

(1)求抛物线C和圆M的方程;

(2)设A1,A2,A3是C上的三个点,直线A1A2,A1A3均与圆M相切.判断直线A2A3与圆M的位置关系,并说明理由.

(1)抛物线C:y2＝x,圆M:(x－2)2＋y2＝1(求解过程略).

所以直线A2A3与圆M相切.当直线斜率不存在时,可以验证该结论也成立.

综上,若直线A1A2,A1A3与圆M相切,则直线A2A3与圆M相切.

点评方法1的关键是把式①整理为关于y2的一元二次方程,从而同构出关于y的一元二次方程,且认定y2,y3为该方程的两根,借助根与系数的关系完成计算.其实我们也可以把式①整理为关于x2,y2的二元一次方程来使用.

变式已知抛物线y2＝2px上的点M(m,0)(m＞0),是否存在以M为圆心,r为半径的圆M,使得对于C上三个点A1,A2,A3,当直线A1A2,A1A3均与圆M相切时,必有直线A2A3与圆M也相切?若存在,则圆M的半径r与m有何关系?

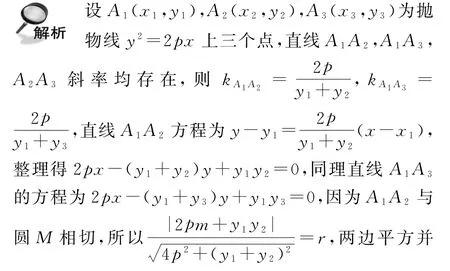
由式①得2pm－2pr＝r2,把该式代入式②化简,可得16p3r4＝16p3r4恒成立;把2pm－2pr＝r2代入式③化简,可得(2pr3)2＝4p2r6恒成立.由此可得,若直线A1A2,A1A3均与圆M相切,当r满足r2＋2pr－2pm＝0时,必有直线A2A3与圆M也相切.

当有直线斜率不存在时,可以验证该结论也成立,即满足条件的圆其实有很多个,只要当r满足r2＋2pr－2pm＝0即可.

点评其实例5的本质就是彭赛列闭合定理的一类特殊情况,变式相当于用初等数学的方法对这类特殊情况进行了一般化的证明,而这种同构思想也正是我们解决圆锥曲线问题的一种重要技巧.

方程的异化与同构本质都是对方程结构的灵活运用,其实这种思想在数学中是极其重要的,特别地,在数学中用迭代算法求根、用不动点法求通项公式等时都会使用.要想运用好该思想,我们必须明确目的,根据目的进行针对性转化,从而更好地利用方程的结构巧妙地解决问题.

(完)