三棱锥外接球常见题型分析及解题策略

龙成芳

(贵州省天柱民族中学)

立体几何的外接球问题是高考考查的热点,能集中考查数学核心素养的逻辑推理、数学建模、直观想象和数学运算等,同时也容易创设情境,所以这类题是值得重视的.这类题型主要集中于三棱锥的外接球,这是一种常规题型,在解题方面有很多研究结果,也分得很细,但本人认为分两类即可:一类是存在一条棱和表面垂直的三棱锥,这是最常见的一种;另一类是没有棱和表面垂直的三棱锥,这又具体表现在正三棱锥、一条棱所对的所有角均为直角的三棱锥、已知二面角的三棱锥和长方体面对角线为棱的三棱锥.

解决这类问题的核心思想是确定球心位置,所以解题的关键在于寻找外接球的球心,要确定外接球球心,首先要明确三棱锥和球的关系:三棱锥是球的内接三棱锥.如果以三棱锥的任何一个表面为截面对球进行切割,得到球的截面一定是圆,这个圆同时也是三棱锥这个表面三角形的外接圆,若把这个圆的圆心与球心连接起来,这条线必然和截面垂直,即直线和三棱锥的这个表面垂直.反过来,在三棱锥的表面找到这个面的外接圆圆心,作该面的垂线,则三棱锥的外接球球心必然在这条垂线上.这是解决这类问题的主要依据,也是核心所在.

1 有棱和表面垂直的三棱锥外接球问题

例1已知三棱锥A-BCD的所有顶点都在球O的球面上,且AB⊥平面BCD,AB＝＝AD＝4,CD＝2,则球O的表面积为( ).

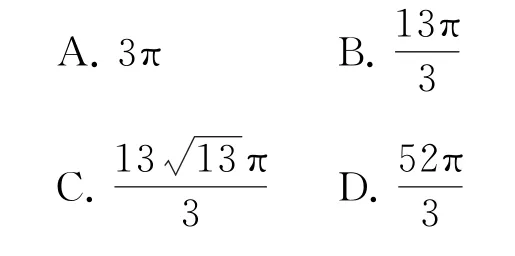
分析如图1所示,题目明确已知在三棱锥A-BCD中,AB⊥平面BCD,由此题型得以确定,接下来就是找球O的球心,根据三棱锥与球O的位置关系,找到△BCD的外心,记为O1,过点O1作平面BCD的垂线l,则三棱锥A-BCD的外接球球心定在直线l上.由已知得l∥AB,故有AB,从而选择以O,O1和三棱锥A-BCD的任意一个顶点构造一个三角形,通过解这个三角形就能求出球O的半径.

图1

解找到△BCD的外心,记为O1,过点O1作平面BCD的垂线,记为l,在直线l上找一个异于点O1的点O,连接O1C和OC,如图2所示.

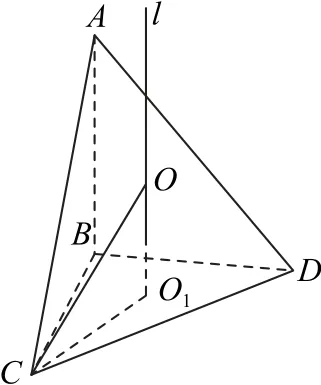
图2

点评这类题型是三棱锥外接球问题中最常见的一种,题目的主要特征是三棱锥的一条棱和表面垂直,建立解题模型的主要依据是球截面圆的圆心和球心的连线与截面垂直,以此确定球心;根据球心与三棱锥的顶点的连线为半径构造三角形,通过解三角形可以求出半径.值得注意的是要会识别,识别的标志是“线面垂直”,即三棱锥的棱和表面垂直,在寻找棱和表面垂直时,要从不同的角度观察,有的题目甚至不会明确告诉棱和表面垂直的关系,需要去发现和证明.同时,这里的“线面垂直”中的线一定是三棱锥的棱,面是三棱锥的表面.在找三角形的外心时,正三角形的外心是三角形的中心,直角三角形的外心是斜边的中点,一般三角形的外心比较难找,但可以借助正弦定理解决,后面几种题型也是一样.

2 正三棱锥的外接球问题

例2在正三棱锥P-ABC中,已知AB＝4,求三棱锥P-ABC的外接球的体积.

分析因为是正三棱锥P-ABC,所以△ABC是等边三角形,则△ABC的“三心合一”,故顶点P在底面的射影与△ABC外心重合.若过△ABC的外心作平面ABC的垂线,则必过点P,且外接球球心也必然在垂线上,然后构造三角形求半径即可.

解如图3 所示,找到△ABC的外心,记为点O1,连接PO1,则有PO1⊥平面ABC,在线段PO1上找一点,记为O,连接线段OB,O1B.

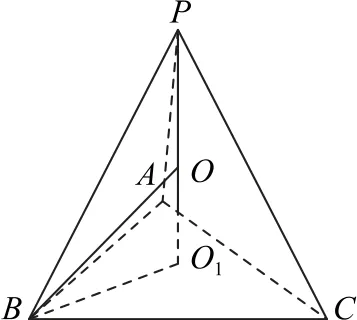
图3

因为点O1是△ABC的中心,所以

点评正三棱锥也包括正四面体,正四面体也是一个正方体的面对角线组成的三棱锥,所以正方体的面对角线组成的三棱锥不作为一种题型研究,这类题型的特征很明显,就是正三棱锥.在实际解题中,可以直接过顶点作底面(正三角形)的垂线,垂足就是底面三角形的外心.当然,上面我们是直接把球心放在底面的上方计算的,球心也有可能在下方,判断外接球球心在三棱锥底面上方还是下方,主要根据三棱锥的高和外接球半径的大小关系.当R＞h时,球心在底面下方;当R＜h时,球心在底面上方.实际上,根据以上计算方法,不管球心在底面上方还是下方,对计算结果没有影响.

3 三棱锥中一条棱所对的所有角均为直角的外接球问题

例3如图4所示,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,PA＝AB＝BC＝3,则该三棱锥外接球的表面积为( ).

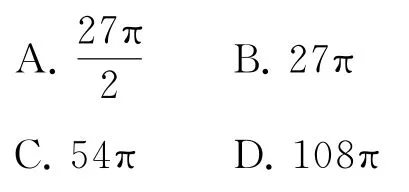
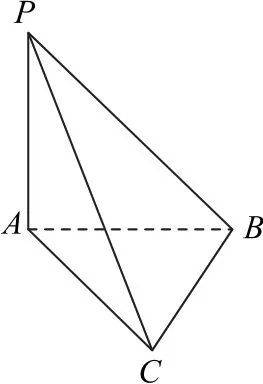
图4

分析由于PA⊥平面ABC,故可以按照例1的方法来求解,但在这里主要体现一下另一种独特解法.题目有AB⊥BC,所以∠PBC＝∠PAC＝90°,也就是说在三棱锥P-ABC中,棱PC所对的角均为直角,根据直径所对的角为直角,可知PC就是三棱锥P-ABC外接球的直径.

解因为PA⊥平面ABC,所以PA⊥AC,PA⊥BC.又因为AB⊥BC,所以BC⊥平面PAB,故有PB⊥BC,所以PC就是三棱锥P-ABC外接球的直径,则

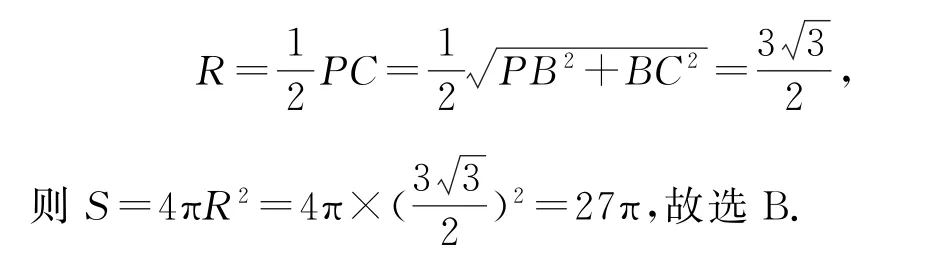
点评题型识别标志是三棱锥中有棱所对的角均为直角,值得说明的是这里三棱锥的棱所对的角的顶点必须是三棱锥的顶点,建立数学模型的依据是球的直径所对的“球周角”为直角.

4 已知二面角的三棱锥外接球问题

例4如图5所示,在平行四边形ABCD中,若AC＝AB＝4,∠BAD＝120°,将△ABC沿对角线AC翻折至△AB1C所在的位置,使得二面角B1-AC-D的大小为120°,则过A,B1,C,D四点的外接球的表面积为________.

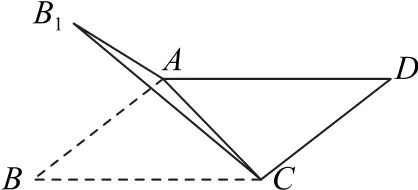
图5

分析这种题型的特征是有“二面角B1-AC-D的大小为120°”,所以解题要围绕这一点.由△ACD和△AB1C均为正三角形,过△ACD的外心O1作平面ACD的垂线,球心必然在垂线上;同样过△AB1C的外心O2作平面AB1C的垂线,球心也必然在垂线上,则两条垂线的交点O就是外接球球心,过点O1作O1M⊥AC交AC于M,构造△OO1M和△OCM,解出OC即可.

解如图6 所示,找到△ACD的外心O1,过点O1作平面ACD的垂线,找到△AB1C的外心O2,过点O2作平面ACD的垂线,两垂线交于一点O,则点O为三棱锥B1-ACD外接球的球心.过点O1作AC的垂线,垂足为M,连接OC,OM,O1M.

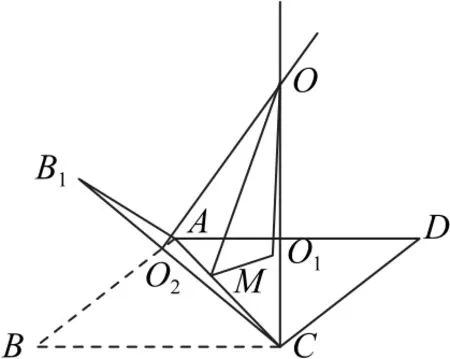
图6

因为△ACD是等边三角形,所以点O1为重心,则

又二面角B1-AC-D的大小为120°,所以∠OMO1＝60°,则

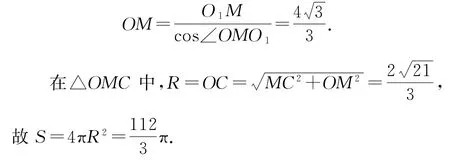
点评这种题型稍微复杂一点,识别标志是在三棱锥中,已知两个表面的二面角大小,建模的主要依据就是过三棱锥的表面外心作垂线,球心必在垂线上,如果作两条及以上这样的垂线,交点必为球心.

5 长方体的面对角线构成三棱锥的外接球问题

例5如图7所示,在三棱锥P-ABC中,PA＝＝AC＝2,PC＝AB＝,则 三棱锥P-ABC外接球的体积为( ).

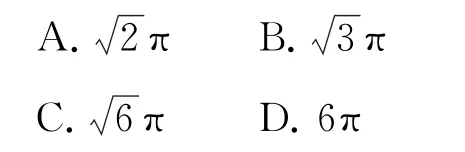
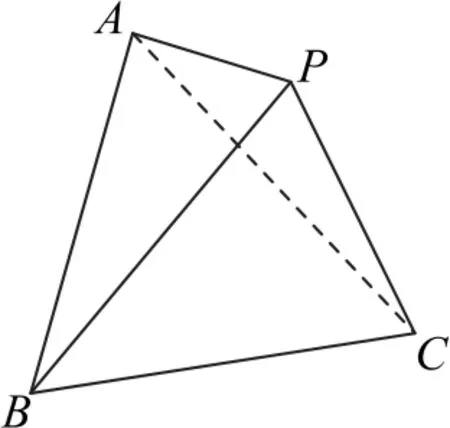
图7

分析这种题型首先要会识别,主要的特征是三棱锥相对的各组棱长相等.解这种题只需要将三棱锥放入长方体中,利用长方体的面对角线分别求出长方体的长、宽、高,再用体对角线公式求出长方体的体对角线,即为三棱锥外接球直径.

点评这种题的识别标志是三棱锥的三组对棱分别相等,建模的主要依据是要把这个三棱锥放入对应的长方体中,三棱锥的对应棱是所在长方体的面对角线.

以上就是三棱锥的外接球相关问题的五种常见题型,题型没有过于细分,方法也没有所谓秒杀的技巧,是对知识的直接体现,是笔者长期教学中的一点经验,希望能起到抛砖引玉的作用.

链接练习

1.已知三棱锥P-ABC的四个顶点在球O的球面上,PA＝PB＝PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF＝90°,则球O的体积为( ).

2.已知三棱锥P-ABC中,PA＝PB＝1,AB＝BC,∠APB＝∠ABC＝90°,若二面角P-AB-C的大 小为120°,则三棱锥P-ABC的外接球的表面积为( ).

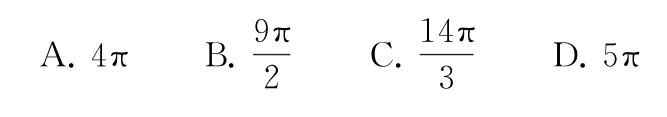
3.如图8所示,已知球O的面上四点A,B,C,D,DA⊥平面ABC.AB⊥BC,DA＝AB＝BC＝,则球O的体积等于_________.

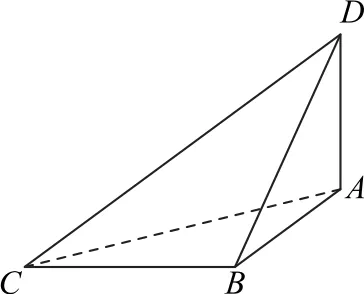
图8

4.已知三棱锥A-BCD中,AB⊥平面BCD,∠BCD＝90°,AB＝BC＝2,CD＝,则三棱锥的外接球的体积为________.

链接练习参考答案

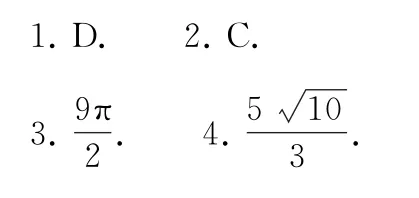
(完)