激活思维,提高效率——妙解正方体中的动点问题

王丽君 孙丕训(特级教师)

(北京陈经纶中学)

立体几何中的动点问题一直是高考典型的难点问题,对学生的逻辑推理和直观想象等核心素养要求较高.而正方体是学生最熟悉的几何模型,所以高考试题中频繁出现以正方体为载体的位置关系计数类问题、动点轨迹类问题、向量的数量积的取值范围问题、构建新的几何体问题等.如何打破思维常规,巧妙应对这些创新的小题? 对此笔者通过归纳整理、列举典例,以高三试题中的压轴题为例进行剖析.

1 位置关系计数类

1.1 平行

例1如图1所示,已知点E,F分别是正方体ABCD-A1B1C1D1的棱AB,AA1的中点,点M,N分别是线段D1E与C1F上的点,则满足与平面ABCD平行的直线MN有( ).

图1

A.0条 B.1条 C.2条 D.无数条

解析这是一道双动点问题,D1E与C1F是两条异面直线,M,N分别是线段D1E与C1F上的点.因为是正方体,容易想到建立空间直角坐标系,设出M,N的坐标,要使MN∥平面ABCD,只需MN与平面ABCD的法向量D1D垂直.不难得出有无数解,从而满足条件的直线MN有无数条.若不动笔算,可以转换思路:显然C1D1∥平面ABCD,过点F可作一个平面与平面ABCD平行且与线段D1E交于一点,这样已经找出2条了,然后让平面ABCD向上运动,从点F开始后,它总会和线段D1E,C1F分别有1个交点,即为点M,N,这样的平面有无数多个,因此,与平面ABCD平行的直线MN有无数条,故选D.

变式已知E,F分别为正方体ABCDA1B1C1D1的棱AB,AA1上的点,且AE＝mAB,AF＝nAA1,m,n∈(0,1),M,N分别为线段D1E和C1F上的点,则与平面ABCD平行的直线MN有( ).

A.1条 B.3条 C.6条 D.无数条

答案D.

1.2 垂直

例2如图2 所示,已知点E,F分别是正方体ABCD-A1B1C1D1的 棱AB,AA1的中点,点M,N分别是线段D1E与C1F上的点,则与平面ABCD垂直的直线MN有( ).

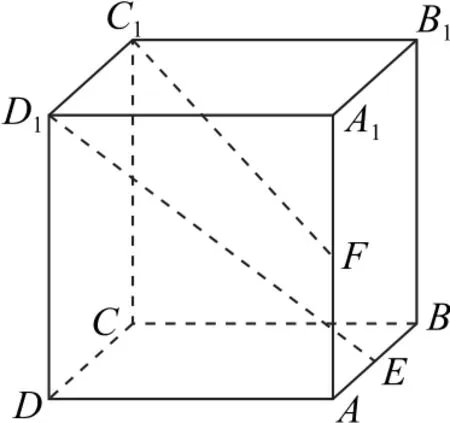
图2

A.0条 B.1条

C.2条 D.无数条

解析本题情境与例1 类似,问题变化为垂直关系,可类比思考:显然DD1⊥平面ABCD,让DD1沿着D1E的方向运动,则这条动直线和线段C1F只有1个交点,交点为线段D1E和C1F在平面ABCD的投影的交点,即线段DE和AC的交点H(如图3),故选B.

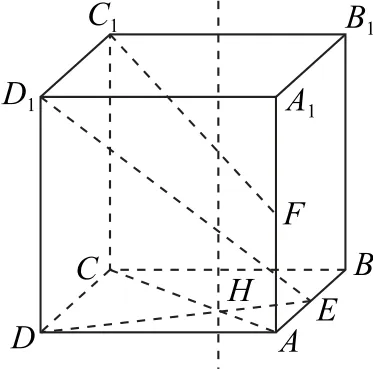
图3

变式已知E,F分别为正方体ABCD-A1B1C1D1的棱AB,AA1上的点,且AE＝mAB,AF＝nAA1,m,n∈(0,1),M,N分别为线段D1E和C1F上的点,则与平面ABCD垂直的直线MN有( ).

A.1条 B.3条 C.6条 D.无数条

答案A.

点评对于上述平行、垂直的关系问题,可以通过移动平面和直线,产生一部分相对静态的位置和不变的量,从而达到“以动制动”的效果.

1.3 等距离

例3与正方体ABCD-A1B1C1D1的三条棱AB,CC1,A1D1所在直线的距离相等的点( ).

A.有且只有1个 B.有且只有2个

C.有且只有3个 D.有无数个

解析由特殊位置想到点B1,D到三条棱AB,CC1,A1D1所在直线的距离都为棱长.根据对称性,想到B1D的中点(也是正方体的中心)到三条棱AB,CC1,A1D1所在直线的距离都为棱长的倍,那么线段B1D上的其他的点可以吗? 设点J是线段B1D上的任意一点,且DJ＝λDB1,λ∈(0,1),设正方体的棱长为1.作JK⊥平面ABCD,KL⊥AD,延长LK交BC于M,则KM⊥BC,如图4 所示,易知点J到棱AB所在直线的距离为,点J到棱CC1所在直线的距离为

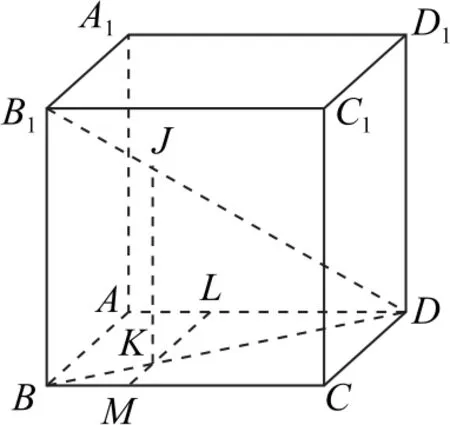
图4

同理可得点J到棱A1D1所在直线的距离为,即线段B1D上的任意一点都满足题意,故选D.

1.4 等夹角

例4如图5所示,过正方体ABCD-A1B1C1D1的顶点A作直线l,使l与直线AB,AD,AA1所成角都相等,这样的直线l可以作( ).

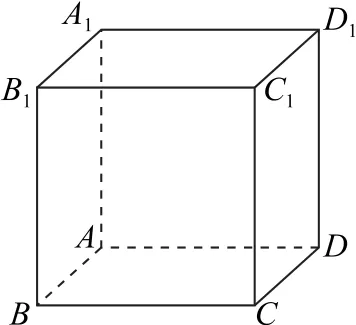
图5

A.1条 B.2条

C.3条 D.4条

解析与直线AB,AD所成角都相等的直线在∠BAD(或其补角)的角平分面上.同理与直线AD,AA1所成角都相等的直线在∠A1AD(或其补角)的角平分面上.这两组角平分面的交线为过点A的4条直线,这样相当于再补3个过点A的全等正方体(如图6),以A为顶点的4条体对角线所在直线即为符合要求的4条直线,故选D.

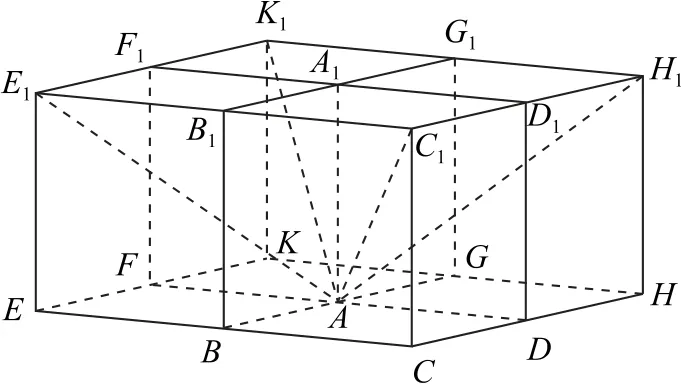
图6

变式在正方体ABCD-A1B1C1D1中,记过点A与直线AB,直线AD,直线AA1所成角都相等的直线条数为m,过点A与三个平面AB1,AC,AD1所成角都相等的直线的条数为n,则下面结论正确的是( ).

A.m＝1,n＝1 B.m＝4,n＝1

C.m＝3,n＝4 D.m＝4,n＝4

答案D.

点评解决这两类问题通常都是从特殊到一般,先想到一个位置,类比迁移进而会得到其他的位置,并思考如下问题:空间中到两个点距离相等的轨迹是什么,到两条直线距离相等的点的轨迹什么,到两个面距离相等的点的轨迹什么,与两条直线夹角相等的点的轨迹什么?这样的整体观念更有助于解决立体几何动点问题.

2 动点轨迹类问题

2.1 形状问题

例5如图7所示,在正方体ABCD-A1B1C1D1中,已知点P为底面ABCD上的动点,PE⊥A1C于E,且PA＝PE,则点P的轨迹是( ).

图7

A.线段

B.圆弧

C.椭圆的一部分

D.抛物线的一部分

解析如图8 所示,连接A1P,则PA＝PE,AA1⊥AP,PE⊥A1C,故Rt△A1AP≌Rt△A1EP,因此AA1＝A1E,所以点E是定点,又因为PA＝PE,所以点P在线段AE的中垂面与平面ABCD的交线上,所以轨迹是线段,故选A.

图8

2.2 面积定值问题

例6已知正方体ABCD-A1B1C1D1(如图9)的棱长为2,E是棱D1C1的中点,点F在正方体内部或正方体的表面上,且EF∥平面A1BC1,则动点F的轨迹所形成的区域面积是( ).

图9

解析如图10 所示,只需过点E作与平面A1BC1平行的平面,即在平面A1B1C1D1上过点E作EH∥A1C1,在平面CDD1C1上过点E作EN∥A1B.因为两条相交直线确定一个平面,所以只需把平面HEN延伸,找到与正方体ABCD-A1B1C1D1的交线即可,即点F的轨迹所形成的区域是边长为的正六边形EHGQMN,其面积为3,故选C.

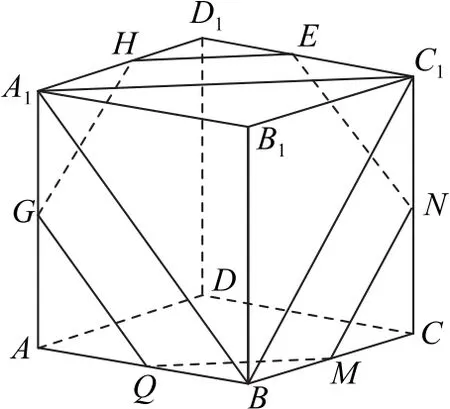
图10

变式已知正方体ABCD-A1B1C1D1的棱长为2,P是底面ABCD上的动点,PA≥PC1,则满足条件的点P构成的图形的面积等于( ).

解析要知道动点P的轨迹,可先考虑临界值,当PA＝PC1时,点P在线段AC1的中垂面上,即在正六边形EFGHMN(如图11)上,因为PA≥PC1,所以动点P的轨迹为△CHM边界及其内部,故选A.

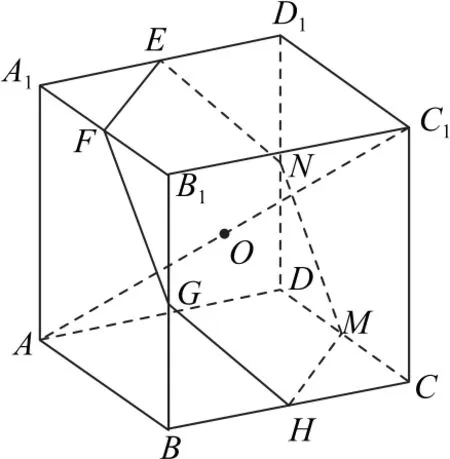
图11

2.3 长度范围问题

例7如图12所示,点M,N分别是棱长为2的正方体ABCD-A1B1C1D1中棱BC,CC1的中点,动点P在正方形BCC1B1(包括边界)内运动.若PA1∥平面AMN,则PA1长度的范围是( ).

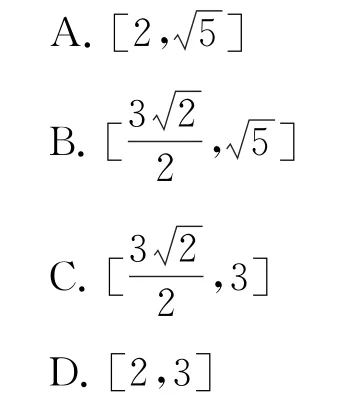
图12

解析要求PA1长度的范围,首先要知道动点P的轨迹,因为PA1∥平面AMN,所 以只需过点A1作一个与平面AMN平行的平面.如图13所示,取B1C1的中点E,取B1B的中点F,则A1E∥AM,EF∥MN,因此平面A1EF∥平面AMN,所以动点P的轨迹为线段EF,故选B.

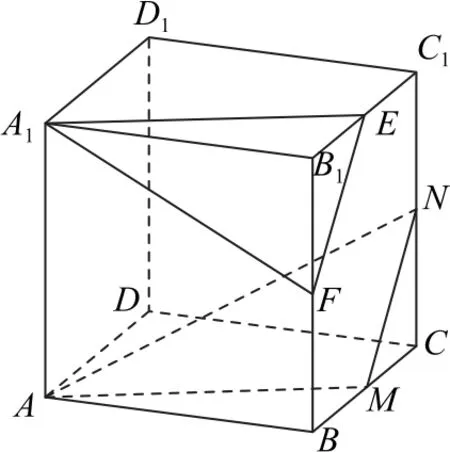
图13

2.4 面积最值问题

例8如图14所示,已知正方体ABCDA1B1C1D1的棱长为2,点O为底面ABCD的中心,点P在侧面BB1C1C的边界及其内部运动.若D1O⊥OP,则△D1C1P面积的最大值为( ).

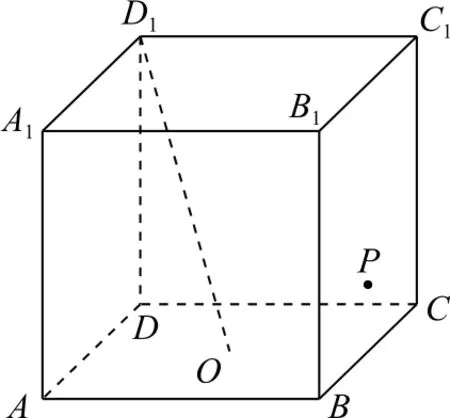
图14

解析本题首先需要知道点P的轨迹,已知D1O⊥OP,只需过点O作出D1O的垂面,显然D1O⊥AC,下一步只需过点A(或C)作直线l⊥D1O即可,如图15 所示,因为D1O在平面ABB1A1的投影为A1F,由三垂线定理知,取B1B的中点E,则AE⊥A1F,即AE⊥D1O,所以D1O⊥平面ACE.又点P在侧面BB1C1C的边界及其内部运动,所以点P的轨迹为线段CE.因此△D1C1P面积的最大值即为点C1与线段CE上的点连线段的最大值,显然为C1E＝,故选C.

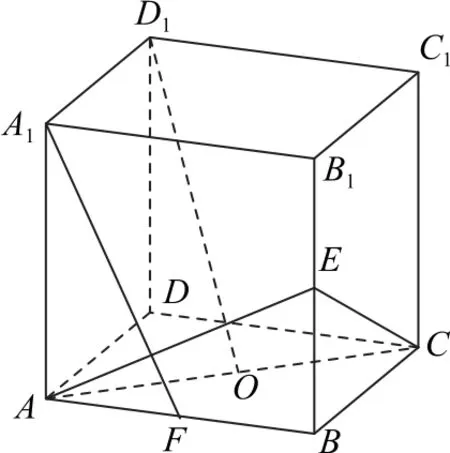
图15

变式1正方体ABCD-A1B1C1D1的棱长为2,点O为底面ABCD的中心,点P在侧面BB1C1C的边界及其内部运动.若D1O⊥OP,则△D1C1P面积的最小值为( ).

答案B.

变式2如图16 所示,在正方体ABCDA1B1C1D1中,M,N分别是棱AB,BB1的中点,点P在体对角线CA1上运动.当△PMN的面积取得最小值时,点P的位置是( ).

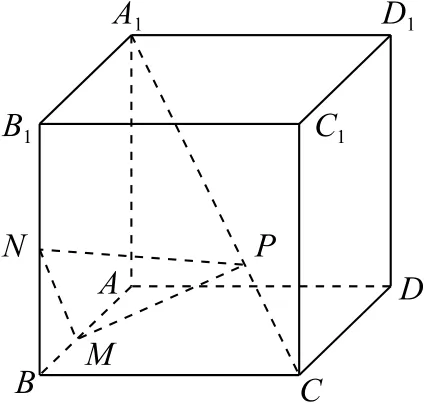
图16

A.线段CA1的三等分点,且靠近点A1

B.线段CA1的中点

C.线段CA1的三等分点,且靠近点C

D.线段CA1的四等分点,且靠近点C

答案B.

点评求解轨迹类问题的第1 步就是要确定动点轨迹的位置,一般都需要通过线面平行、线面垂直的判定、性质定理进行推理,确定位置后再计算长度、面积等.

3 向量的数量积的取值范围类问题

例9点P是棱长为1 的正方体ABCDA1B1C1D1的底面A1B1C1D1上一点,则的取值范围是( ).

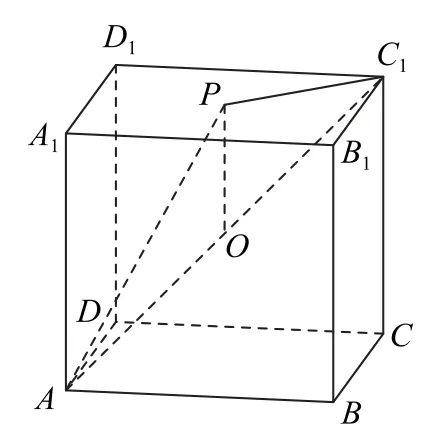
图17

变式如图18所示,正方体ABCD-A1B1C1D1的棱长为1,若动点_P在线段BD1上运动,则的取值范围是________.

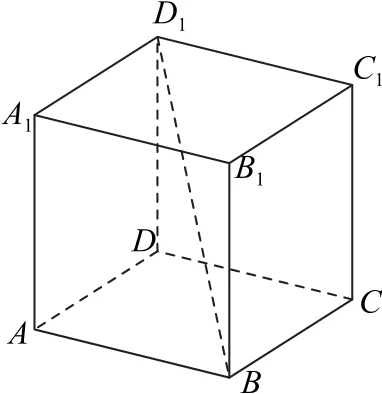
图18

答案[0,1].

点评坐标法是求解向量的数量积问题的基本方法,但本题用极化恒等式与数形结合能快速解题.

4 构建新的几何体求值问题

例10如图19所示,正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱,若此三棱柱另一底面三个顶点也都在该正方体的表面上,则这个正三棱柱的高h为_________.

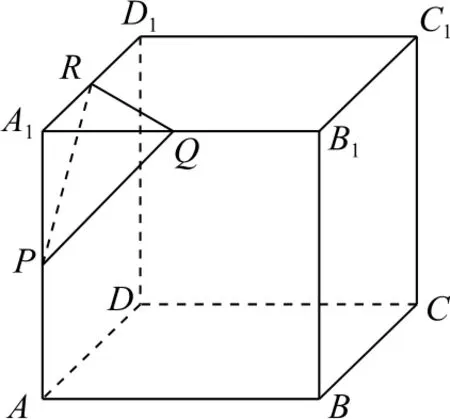
图19

解析如图20 所示,因为体对角线A1C⊥平面PQR,所以只需过P作PP1∥A1C交平面ABCD于点P1.同理,可以分别作QQ1∥A1C,RR1∥A1C,所 以得到正三棱柱PQRP1Q1R1,该正三棱柱的高为

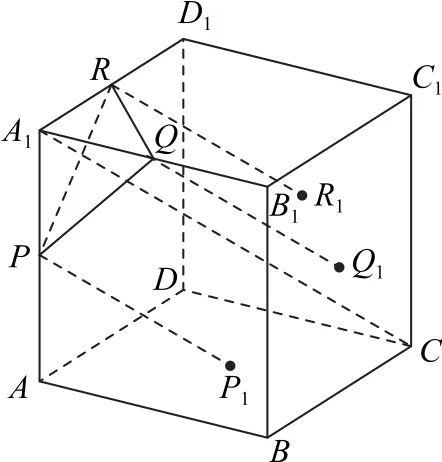
图20

变式以棱长为1的正方体各面的中心为顶点构成一个正八面体,再以这个正八面体各面的中心为顶点构成一个小正方体,那么该小正方体的棱长为( ).

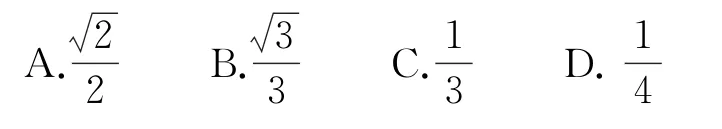
答案C.

点评这类问题抓住新的几何体特点,紧扣定义,并充分利用正方体的体对角线与面AB1D1垂直的性质解决问题.

(完)