几何推理,坐标运算
——一道动态立体几何题的探究
周 波
(山东省济南市章丘区第五中学)
周 波
(山东省济南市章丘区第五中学)
多选题是新高考中体现“破定势,考真功,分层次”的一种创新题型,可以很好地考查学生“四基”的落实情况,区分数学能力,备受各方关注.而涉及立体几何知识的多选题,更是其中常见的基础题之一.多选题的创新设置,可以很好地考查立体几何中点线面的位置关系、长度或距离、夹角以及面积、体积等问题,以及动点、折叠、旋转等动态问题.
1 问题呈现
题目(多选题)如图1 所示,已知直四棱柱ABCD-EFGH的底面是边长为4 的正方形,CG=m,点M为CG的中点,点P为底面EFGH上的动点,则( ).

图1
A.当m=4时,存在点P满足PA+PM=8
B.当m=4时,存在唯一的点P满足∠APM=
C.当m=4 时,满足BP⊥AM的点P的轨迹长度为
D.当m=时,满足∠APM=的点P的轨迹长度为
分析此题是一道立体几何中的动态问题,以长方体为背景进行巧妙设置,常见的解题思路有两种:
1)建立空间直角坐标系,利用坐标法进行求解,考查数学运算能力;
2)利用几何法,通过综合分析处理与求解,考查推理论证能力.
解法1(坐标法)以D为坐标原点,分别以射线DA,DC,DH所在直线为x轴,y轴,z轴的正半轴,建立空间直角坐标系D-xyz,如图2所示,则D(0,0,0),A(4,0,0),B(4,4,0),C(0,4,0),M(0,4,),设P(x,y,m).
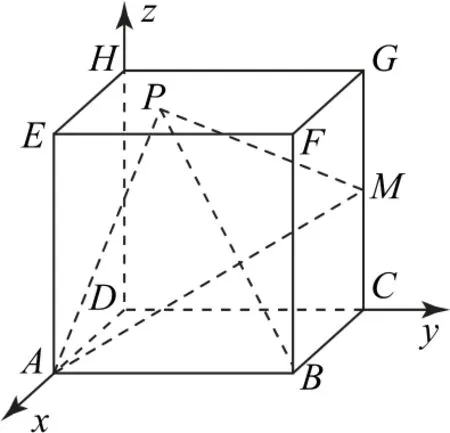
图2
对于选项A,当m=4时,设点M(0,4,2)关于平面EFGH的对称点为M1,则M1(0,4,6),故|PA|+|PM|=|PA|+|PM1|≥,故选项A 错误.


综上,选BCD.
点评坐标法是大家比较熟悉的一种方法,借助长方体这个特殊立体几何模型,合理构建空间直角坐标系,通过确定点的坐标以及向量的坐标运算,结合数量积的应用来分析与转化,实现问题的坐标代数化处理.
解法2(几何法)对于选项A,当m=4时,设点M关于平面EFGH的对称点为M1,则CM1=6,所以PA+PM=PA+PM1≥AM1=,故选项A 错误.
对于选项 B,当m=4 时,可得AM==6,由于线段AM的中点O到平面EFGH的距离为3,所以以点O为球心,3为半径的球与平面EFGH相切于正方形EFGH的中心O′,即存在唯一的点P(此时点P与点O′重合)满足∠APM=,故选项B正确.


综上,选BCD.
点评几何法是解决立体几何问题中的一种常用方法,通过点线面的位置关系以及对应边、角等的大小关系,利用立体几何、平面几何的相关知识加以分析与处理,合理巧妙解决对应的立体几何问题,对空间想象、逻辑推理以及数学运算等方面的能力要求较高.
2 变式拓展
变式1(多选题)如图3所示,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥平面ABCD,SA=AB,O,P分别是AC,SC的中点,M是棱SD上的动点,则( ).

图3
A.OM⊥AP
B.存在点M,使得OM∥平面SBC
C.存在点M,使得直线OM与AB所成角为30°
D.点M到平面ABCD与平面SAB的距离之和为定值
答案ABD.
变式2(多选题)如图4所示,已知正方体ABCDEFGH的棱长为2,M为棱CG的中点,P为底面EFGH上的动点,则( ).

图4
A.存在点P,使得AP+PM=4
B.存在唯一点P,使得AP⊥PM
C.当AM⊥BP时,点P的轨迹长度为
D.当点P为底面EFGH的中心时,三棱锥P-ABM的外接球体积为
答案BCD.
(完)

