立体几何中的易错点分析

方 奔

(安徽省蒙城县第六中学)

立体几何问题中经常出现一些容易致误的问题,本文针对立体几何问题中的典型问题进行分析,并对这些问题中的易错点进行分析,从而能有效地避免“雷区”.

1 忽视空间线面位置的多重性

例1已知α,β是空间中两个不同的平面,m,n是空间中两条不同的直线,则下列说法中正确的是( ).

①m∥α,n∥β,且m∥n,则α∥β;

②m∥α,n∥β,且m⊥n,则α⊥β;

③m⊥α,n⊥β,且m∥n,则α∥β;

④m⊥α,n⊥β,且m⊥n,则α⊥β.

A.①②③B.①③④

C.②④ D.③④

解析对于①,当m∥α,n∥β,且m∥n时,有α∥β或α,β相交,所以①错误.对于②,当m∥α,n∥β,且m⊥n时,有α⊥β或α∥β或α,β相交且不垂直,所以②错误.对于③,当m⊥α,n⊥β,且m∥n时,得出m⊥β,所以α∥β,③正确.对于④,当m⊥α,n⊥β,且m⊥n时,α⊥β成立,所以④正确.

综上,正确的命题序号是③④,故选D.

点评本题考查了空间中线面平行与垂直关系的判断.本题易错选B,误用一组线线平行去推面面平行.判断空间中线面、面面位置关系时易忽略空间线面位置关系的多样性.破解此类问题的关键是熟知空间中的线线、线面、面面位置关系的判定与性质,要注意定理条件的完整性.除此之外,还可以借助一些特殊载体,如长方体、三棱锥等,将相关的直线、平面放到相应载体中观察,使得空间线面、面面的位置关系得到多视角的验证.

2 忽视平面图形翻折前后的显性关系

例2如图1 所示,在矩形ABCD中,AB＝2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则 在△ADE翻折过程中,给出以下命题:

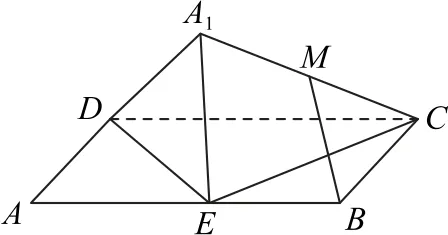
图1

①存在某个位置,使BM∥平面A1DE;

②存在某个位置,使DE⊥A1C;

③线段BM的长是定值;

④存在某个位置,使MB⊥平面A1CD.其中所有正确命题的编号是( ).

A.①② B.①③C.②④ D.①③④

解析如图2所示,取A1D的中点N,连接MN,NE,则MN∥CD,MN＝CD.又EB∥CD,E为边AB的中点,所以,MN∥EB,MN＝EB,所以四边形MNEB是平行四边形,故BM∥NE.又BM⊄平面A1DE,NE⊂平面A1DE,所以BM∥平面A1DE,故①正确.

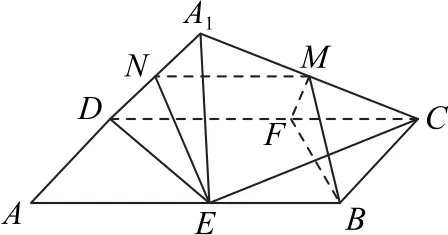
图2

设AB＝2AD＝2,则DE＝CE＝,所以DE2＋CE2＝CD2,故DE⊥CE.若DE⊥A1C成立,因为CE∩A1C＝C,CE⊂平面A1CE,A1C⊂平面A1CE,则DE⊥平 面A1CE,DE⊥A1E,这 与∠DEA1＝∠AED＝45°矛盾,所以DE与A1C不可能垂直,故②错误.

因为BM＝NE,所以BM长为定值,故③正确.

过M作CD的垂线,垂足为F,连接MF,BF,若BM⊥平面A1CD,则BM⊥CD.又CD⊥MF,BM∩MF＝M,BM⊂平面BMF,MF⊂平面BMF,所以CD⊥平面BMF,CD⊥BF,这与BC⊥CD矛盾,故④错误.

综上,选B.

点评本题易错点在于不能明确翻折问题中的变与不变,翻折问题的核心是“折痕”,一条折痕把平面图形分成两部分,与折痕平行或垂直的线段翻折前后平行关系或垂直关系不变.一般情况下,如果一个量的两个要素在折痕同侧,则在翻折前后量是不变的;如果一个量的两个要素在折痕两侧,则在翻折前后量是变化的.

3 未准确把握平面几何中的结论

例3下列命题中正确的个数为( ).

①平行于同一直线的两直线平行;

②平行于同一平面的两直线平行;

③平行于同一直线的两平面平行;

④平行于同一平面的两平面平行.

A.1 B.2 C.3 D.4

解析由平行线的传递性知平行于同一直线的两直线平行,故①正确.平行于同一平面的两直线平行、相交、异面都有可能,故②错误.平行于同一直线的两平面平行、相交都有可能,故③错误.平行于同一平面的两平面平行,故④正确.综上,选B.

点评有关位置关系在平面几何中成立的某些结论,在空间中任意地推广、拓展,有时得出的结论是不成立的.

4 无法准确确定球心的位置

例4在三棱锥P-ABC中,平面PAB⊥平面ABC,△ABC是边长为6 的等边三角形,△PAB是以AB为斜边的等腰直角三角形,则该三棱锥外接球的表面积为________.

解析如图3 所示,在等边△ABC中,取AB的中点F,设△ABC的中心为O,由AB＝6,可得

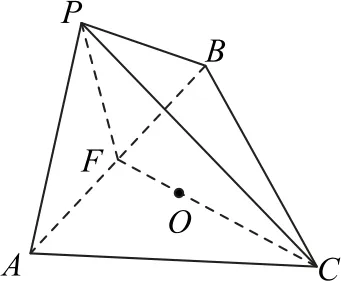
图3

因为△PAB是以AB为斜边的等腰直角三角形,所以PF⊥AB.又平面PAB⊥平面ABC,所以PF⊥平面ABC,PF⊥OF,OP＝,则O为棱锥P-ABC外接球的球心,外接球半径R＝OC＝,所以该三棱锥外接球的表面积为4π×＝48π.

点评空间想象能力差,无法准确作出图像,无法确定球心位置,是求解球与几何体相接问题容易失误的主要原因.

5 误将两向量关系与线面关系等同

例5如图4所示,已知四棱锥P-ABCD的底面是直角梯形,AB∥DC,∠DAB＝90°,PD⊥底 面ABCD,且PD＝DA＝CD＝2AB＝2,点M为PC的中点.

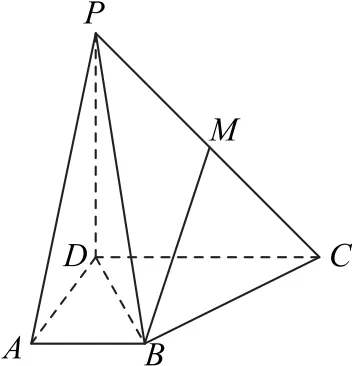
图4

(1)求证:BM∥ 平面PAD;

(2)在平面PAD内找一点N,使MN⊥平面PBD.

解析(1)由 于PD⊥底面ABCD,CD∥AB,CD⊥AD,故以D为原点,DA,DC,DP分别为x轴、y轴、z轴建立如图5所示的空间直角坐标系D-xyz.

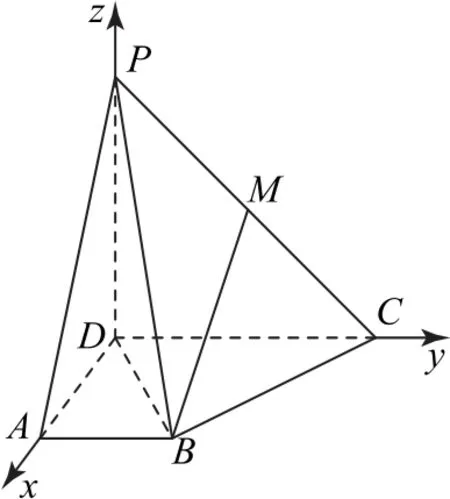
图5

因为PD＝CD＝DA＝2AB＝2,所以A(2,0,0),B(2,1,0),C(0,2,0),P(0,0,2),M(0,1,1).

(完)