例析几何体外接球问题

孙朝鹏

(云南省曲靖市会泽县第一中学校)

对近10年的高考数学试题进行分析,不难发现与立体几何相关的问题常常会出现球的身影,但对于学生而言几何体的外接球和内切球问题具有一定的难度.求解几何体的外接球问题关键在于确定球心位置及球体半径,根据几何体的空间结构特点可以分为不同的外接球模型.本文主要介绍四种不同的三棱锥外接球模型,给学生提供更多几何体外接球问题的求解思路,以便于学习和参考.

1 墙角模型

墙角模型具体是指问题中三棱锥的三条棱满足两两互相垂直条件,求解时可将其补形为长方体(或正方体),进一步按照长方体(或正方体)的外接球思路求解.墙角模型是根据补形后的几何体结构特点形似墙角而命名.

例1在正三棱锥S-ABC中,M,E分别是棱SC,BC的中点,且AM⊥ME,若侧棱SA＝2,则正三棱锥S-ABC外接球的表面积为_________.

解析如图1所示,取AB,BC的中点D,E,连接AE,CD,AE,CD交于点H,连接SH,则点H是底面正△ABC的垂心,所以SH⊥平面ABC,SH⊥AB.

图1

又CD⊥AB,SH∩CD＝H,所 以AB⊥平 面SCD,所以AB⊥SC.同理,BC⊥SA,AC⊥SB,即正三棱锥对棱互相垂直.

如图2 所 示,因 为AM⊥ME,SB∥ME,所 以AM⊥SB.因为AC⊥SB,AM∩AC＝A,所以SB⊥平面SAC,SB⊥SA,SB⊥SC,而SA⊥BC,SB∩BC＝B,所以SA⊥平面SBC,即SA⊥SC,故三棱锥侧棱两两垂直.

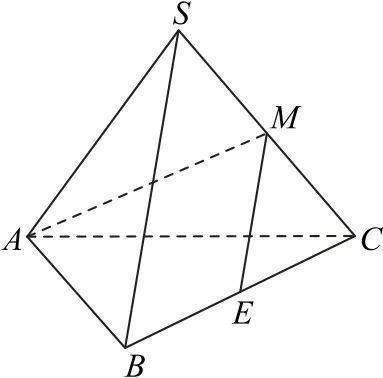
图2

令三棱锥S-ABC的外接球半径为R,如图3 所示,可知正方体的边长 为SA＝SB＝SC＝,则,即R2＝9,S＝4πR2＝36π,故三棱锥S-ABC外接球的表面积为36.

图3

2 对棱相等模型

对棱相等模型实质上是指三组异面棱长相等的三棱锥,可借助这三组棱长求解外接球半径.常见的求解步骤如下:

1)根据问题已知条件,找到三组不在同一平面却相等的棱长,分别求出对应的长度x,y,z;

2)根据勾股定理和墙角模型中的公式2R＝(a,b,c分别为长方体的长、宽、高),将其转化为与棱长x,y,z有关的等式;

3)凭借推导得到R2＝,将棱长代入求得外接球半径.

例2如图4所示,在三棱锥A-BCD中,AB＝CD＝2,AD＝BC＝3,AC＝BD＝4,则三棱锥A-BCD外接球的表面积为_________.

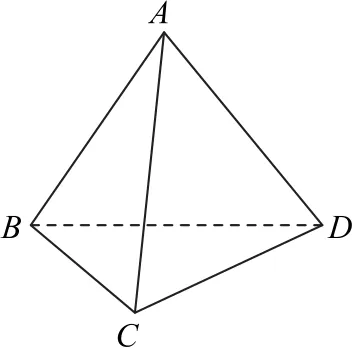
图4

图5

3 垂面模型

垂面模型主要是指锥体有关平面与底面垂直,则此时锥体外接球的球心一定在该平面上,球心的投影为底面外接圆的圆心,根据这些几何关系寻找等价关系式,即可求出锥体外接球的半径.应用垂面模型解答锥体的外接球问题,常见求解步骤如下:

1)在锥体中找到与底面垂直的平面,判断锥体外接球球心O的位置;

2)求解底面图形的外接圆圆心O1与半径r;

3)由于OO1,r,R构成直角三角形,根据勾股定理求出R的大小,即可知锥体外接球的半径及其他值的大小.

例3一个几何体的三视图如图6所示,则该几何体的外接球表面积为( ).

图6

A.3π B.2π

图7

立体几何是高中数学重要的内容,几何体的外接球问题是立体几何中常见的问题.解答有关几何体的外接球问题时,可以尝试运用上述模型进行解答.全面掌握立体几何外接球模型有助于高效解答问题,从而提升解题效率.学习、理解并运用这些不同的外接球模型解答相关问题,也是高中数学的重要学习内容之一.

链接练习

1.正三棱锥A-BCD内接于球O,且底面边长为3,侧棱长为2,则球O的表面积为_________.

2.一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为,底面周长为3,则这个球的体积为________.

3.若长方体外接球体积为36π,则该长方体的表面积最大为________.

4.已知等边△ABC的边长4,且M,N分别为AB,AC的中点,沿着MN将△ABC折成直二面角,则四棱锥A-MNCB外接球的表面积为_________.

链接练习参考答案

(完)