借力空间向量法,巧解折叠问题

魏孝菊

(山东省临沂第一中学)

处理立体几何中有关折叠问题的关键是抓住折叠前后两个图形的特征关系,厘清哪些量发生了变化,哪些量没有发生变化,然后充分利用空间向量法,化繁为简,这样可以有效降低试题难度.显然,解题的起点是考查空间想象能力,落点是考查数学运算求解能力.

1 面面垂直问题

根据折叠后的图形,建立空间直角坐标系,借助空间向量法灵活处理面面垂直问题,其关键是将面面垂直等价转化为两个平面的法向量垂直.

例1如图1 所示,在梯形CEPD中,PD＝8,CE＝6,A为线段PD的中点,ABCD为正方形,现沿AB进行折叠,使得平面PABE⊥平面ABCD,得_到如图2所示的几何体.已知当点F满足(0＜λ＜1)时,平面DEF⊥平面PCE,求λ的值.

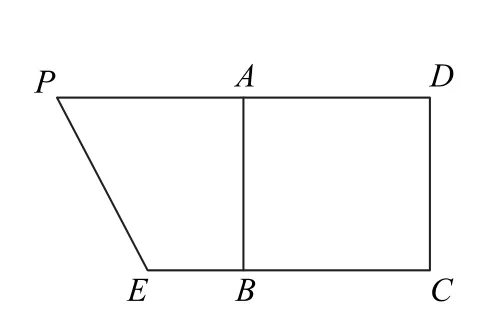
图1

图2

解析如图3 所示,建立空间直角坐标系A-xyz,则 点C(4,4,0),E(4,0,2),P(0,0,4),D(0,4,0).设点F(a,0,0),则＝(4－a,0,2),＝(4,－4,2).

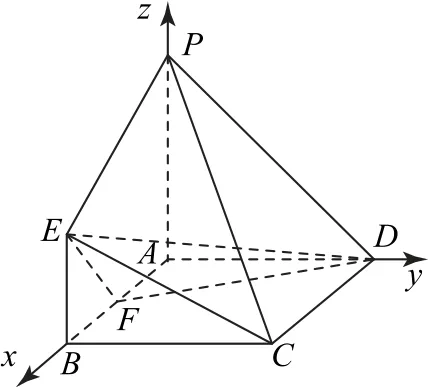
图3

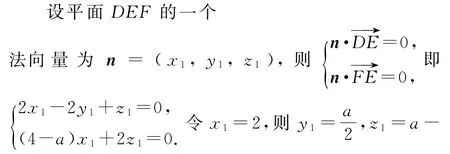
点评一般地,建立空间直角坐标系求平面的法向量时,可以灵活利用待定系数法;特别地,若直线与平面垂直,则容易求得该平面的法向量坐标.

2 线面角问题

根据折叠后的图形,适当建立空间直角坐标系,借助空间向量法灵活处理有关线面角问题,关键是求解平面的法向量、直线的方向向量以及准确利用线面角公式.

例2已知△ABC与△BCD所在平面互相垂直(如图4),且∠BAC＝∠BCD＝90°,AB＝AC,CB＝CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.在翻折后的图形(如图5)中,求直线AP与平面ACQ所成角的大小.

图4

图5

解析取BC的中点O,BD的中点E,建立如图6所示的空间直角坐标系.

图6

不妨设BC＝2,P(x,1－x,0),则A(0,0,1),D(－1,2,0),O(－1,0,0).于是,由|AP|＝|DP|,得x2＋(1－x)2＋1＝(x＋1)2＋(x＋1)2,解得x＝0,所以P(0,1,0)(即P,E重合),故＝(0,1,－1).

点评本题以翻折为载体设置问题,具有一定的难度,求解的关键在于通过适当作辅助线,灵活建立空间直角坐标系,并充分利用平面的法向量巧求线面角.

3 面面角问题

根据折叠后的图形,适当建立空间直角坐标系,借助空间向量法灵活求解二面角的余弦值.方法1是先得到二面角的平面角,再转化为求解具有共同起点的两个向量的夹角的余弦值;方法2是先得到两个平面的法向量,再转化为利用法向量夹角的余弦值巧解目标问题.

例3如图7所示,给出平面图形ABB1A1C1C,其中BB1C1C是矩形,BC＝2,BB1＝4,AB＝AC＝.现将该平面图形分别沿BC和B1C1折叠,使△ABC和△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A1A,A1B,A1C,得到如图8所示的空间图形,试求二面角A-BC-A1的余弦值.

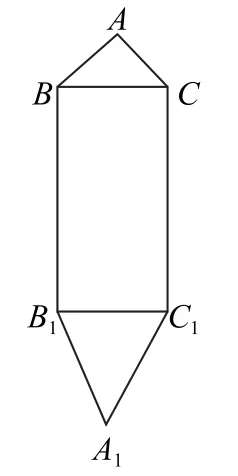
图7

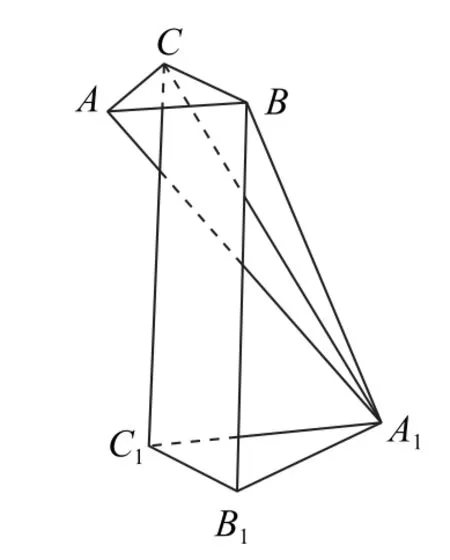
图8

解析设BC,B1C1的中点分别为D和D1,连接A1D1,DD1,AD.由BB1C1C是矩形,知DD1⊥B1C1.又因为平面BB1C1C⊥平面A1B1C1,所以DD1⊥平面A1B1C1.

又由A1B1＝A1C1,知A1D1⊥B1C1,故以D1为坐标原点,建立如图9所示的空间直角坐标系D1-xyz,则由题设可得A1D1＝2,AD＝1.

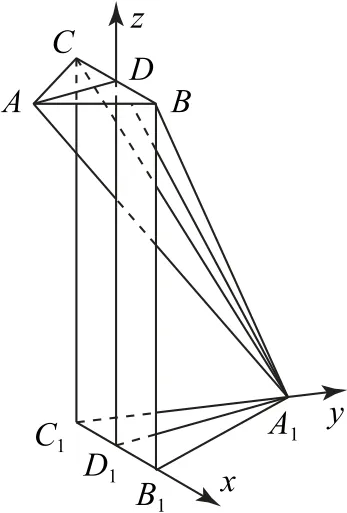
图9

根据等腰三角形“三线合一”的性质易知AD⊥BC,A1D1⊥B1C1,又△ABC和△A1B1C1所在平面都与平面BB1C1C垂直,所以AD⊥平面BB1C1C,A1D1⊥平 面BB1C1C,于 是AD∥A1D1,所以A(0,－1,4),B(1,0,4),A1(0,2,0),C(－1,0,4),D(0,0,4).

连接A1D,则易知BC⊥AD,BC⊥DA1,可得BC⊥平面A1AD,所以BC⊥A1D,所以∠ADA1为二面角A-BC-A1的平面角.

点评本题求解二面角的余弦值,灵活运用了上述方法1.感兴趣的读者还可利用上述方法2进行求解.

通过本文我们可进一步感悟折叠问题的求解过程,加强空间向量知识在解题中的灵活运用,提高空间想象能力、运算求解能力以及数形结合能力,进而提升数学核心素养.

(完)