二面角的平面角的求法面面观

2023-01-07 15:05张平

高中数理化 2022年23期

张平

(广东省珠海市实验中学)

二面角的平面角是立体几何中的一个核心概念,也是高考的重点考查目标.因此厘清如何求解二面角的平面角,明晰求解二面角平面角的常用途径与方法便显得尤为重要.本文在归纳总结二面角的平面角问题求解的主要方法与解题步骤的基础上,结合一道相关试题对每种方法进行了具体分析应用,以期在丰富与完善读者解决此类问题的方法的同时,培养结合题目条件灵活选择方法的意识,提升解决问题的能力.

1 二面角平面角的定义

从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫二面角的棱,这两个半平面叫做二面角的面.在二面角的棱上任取一点O,以点O为垂足,分别在两个半平面内作垂直于棱的射线OA,OB,则射线OA,OB构成的角∠AOB叫做二面角的平面角.根据二面角平面角的定义知∠AOB∈[0,π].

2 二面角平面角的常用求法

2.1 射影面积法

已知平面α内的平面图形Γ的面积为S,它在平面β内的射影Γ′的面积为S′,设平面α与平面β所成二面角的平面角为θ,则当时,当时,cosθ＝

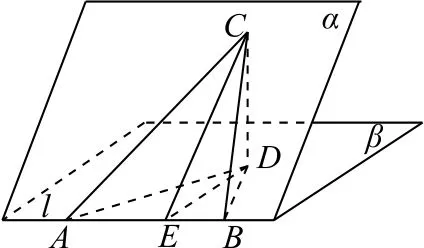
图1

2.2 几何法

1)定义法

用定义法求解二面角平面角的基本步骤为“一找、二算、三得出结论”,首先,结合已知条件及线面垂直关系,作出二面角的平面角,如图1中的∠CED;其次,利用直角三角形计算求解,即求∠CED的三角函数值或角度;最后,根据题目要求得出结论.

2)距离法

由图1知在Rt△DEC中,sin∠CED＝,进而问题转化为分别求平面α内一点C到平面β的距离与到棱l的距离即可.

2.3 坐标法(法向量法)

2.4 向量法(空间向量法)

根据此公式知要求二面角平面角的余弦值,只需在两个半平面内分别“找出”不在棱上的一点,如图2中的点C,D,再分别求出CD,以及点C,D到棱l的距离AC,BD及棱l上两垂足间的距离AB即可.

图2

3 应用举例

题目如图3所示,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PD＝PA＝,PC＝3.

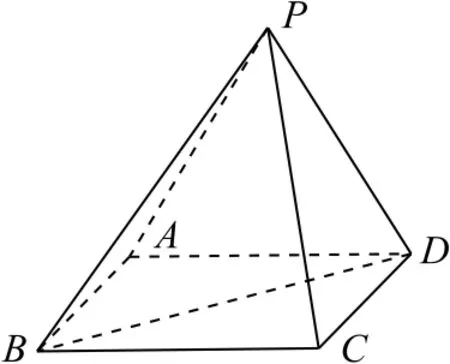
图3

(1)证明:平面PAD⊥平面ABCD;

(2)求二面角B-PD-A的余弦值.

分析第(1)问较为简单,证明过程略.本文用上述方法重点求解第(2)问.

解法1射影面积法

解法2定义法

由解法1 知AB⊥平面PAD,则AB⊥PD.如图4所示,过点A作AM⊥PD于M,连接BM,则AB⊥AM.易证PD⊥平面MAB,从而PD⊥BM,则∠AMB为二面角B-PD-A的平面角.在△PAD中,PD＝PA＝,AD＝2,所以S△APD＝2,AM＝,在Rt△BAM中,有

图4

解法3距离法

由解法1 知AB⊥平面PAD,则点B到平面PAD的距离AB＝2,由解法2知BM⊥PD于M,且BM＝,结合图形知二面角B-PD-A为锐二面角,设二面角B-PD-A的平面角为θ,则

点评解法1～解法3主要是从几何的角度进行求解,而前提是挖掘了“AB⊥平面PAD”这一关键信息,但对这一信息如何使用,有不同的思考与选择.不同的使用方式导致解题方法的区别,体现思维的发散性.

解法4坐标法

图5

结合图形知二面角B-PD-A为锐二面角,则二面角B-PD-A的余弦值为.

点评解法4 是利用坐标法进行求解,首先是将“平面PAD⊥平面ABCD”转化为线面垂直关系,实现建立空间直角坐标系的基本要求,其次是坐标原点与坐标轴的选择,要便于点的坐标表示.其好处在于将几何问题“代数化”,“弱化”了对空间想象能力的考查.

解法5空间向量法

解法6空间向量法

如图6 所示,在△PAD中,过点A作AM⊥PD于M,由解法2可知AM＝,在Rt△PAM中,有

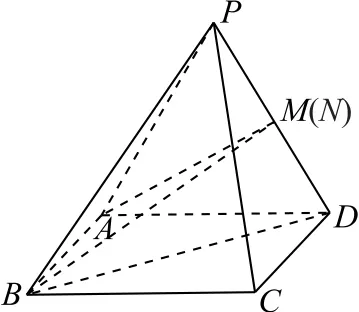
图6

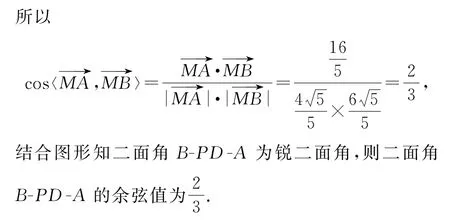
点评解法5～解法7均是利用空间向量法进行求解,虽侧重点有所不同,但均是以“在两个半平面内找与棱垂直的向量”为中心,借助平面向量基本定理、空间向量基本定理及相关运算性质求解.解法5结合坐标法进行运算,简捷快速,解法6与解法7则凸显向量运算性质的应用.

求解二面角的平面角方法众多,首先,要理解掌握常用的求解方法与策略,其次,要具体问题具体分析,通过对题目条件的深入分析、思考与挖掘,找到已知信息与求解方法之间联系的桥梁.同时结合图形特点确定最优求解路径,使用最便捷的方法,快速求解,在提升解题能力的同时完善与发展数学学科素养.

(完)