GeoGebra与高中数学课程融合探究
——以圆锥曲线与方程为例
陈俊艺
(福建省晋江市毓英中学,福建晋江,362251)
圆锥曲线与方程是平面解析几何中的重要内容,重点研究圆锥曲线方程的建立以及利用方程研究曲线的几何性质.基本思路是基于所研究图形的几何特性,建立适当的坐标系,并代数化表达几何图形,借助代数运算变形等手段分析图形的代数表征,获得并解释代数结论,了解几何图形的性质并解决问题.《普通高中数学课程标准(2017年版)》指出:“教师应注重信息技术与数学课程的深度融合, 实现传统教学手段难以达到的效果.” Geogebra是一款兼具代数与几何功能的动态作图软件,在圆锥曲线教学中通过Geogebra直观展示图形的变化过程,探索运动变化过程中的不变性与规律性,再通过代数的方法加以证明. 引导学生关注数学本质,重视数学实验,帮助他们理解数学.下面通过几个案例,探究GeoGebra与高中数学课程融合的方式.
1 案例分析
1.1 轨迹问题
探究动点的轨迹问题是解析几何中的教学重点和难点,如何根据已知条件,寻找点运动的规律,构建出轨迹,求出轨迹方程,对学生的数学抽象和数学建模素养都有较高的要求.借助GeoGebra可以把轨迹的形成过程动态地呈现出来,实现问题的可视化探究,这是传统教学方式比较难于达到的.
案例1圆O的半径为定长r,A是圆O内一定点,P是圆O上任意一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是什么?为什么?
教学分析:我们可以先通过实验观察,直觉地猜想出轨迹,再进行严格的逻辑证明.
具体操作:
(1) 在绘图区的空白位置使用“圆(圆心与一点)”工具绘制圆O,在圆O内任取一点A,同时在圆O上任取一点P;
(2) 使用“线段”工具绘出线段AP,使用“直线”工具绘出OP;
(3) 使用“中垂线”工具,点击线段AP,得到中垂线l;
(4) 使用“交点”工具绘制直线l与OP的交点Q;
(5) 使用“轨迹”工具,依次点选点Q和点P,得到点Q的轨迹,通过观察可以得出点Q的轨迹是一个椭圆(如图1所示).

图1
代数证明:因为|QP|=|QA|,而|QO|+|QA|=|QO|+|QP|=r(定值).
因A在圆内,所以|OA|<|OP|=r.
由椭圆的定义知,点Q的轨迹是以O,A为焦点的椭圆.
借助GeoGebra我们还可以探究以下变式:
变式:将线段OP改为直线,“A是圆O内一定点”,改为“A是圆O外一定点”,其余条件不变,再观察实验现象变化,又能得到什么样的轨迹?
1.2 圆锥曲线的性质
洞察几何对象的几何特征,并选择适当的坐标系将其准确地代数化,从而通过代数运算获得曲线的几何性质,这对于学生理解解析几何的基本思想方法和积累问题解决的经验都是非常有益的.利用GeoGebra既可以方便作图,又可以向学生演示动点的变化规律,引导学生探究曲线的性质.
案例2离心率对椭圆形状的影响

具体操作:
(1) 创建滑动条,定义参数e,并调整参数e的变化范围;
(2) 作两定点.使用“描点”工具在坐标系横轴上任意绘制一点F1作为一个定点(即椭圆的一个焦点),再使用“中心对称”工具,依次点选对称的对象点F1和对称中心点O,得到另一个定点F2(即椭圆的另一个焦点);

(4) 作点的轨迹——椭圆.
在x轴上绘制任意一点C,使用“线段”工具分别作它与A1和A2的连线段,使用“圆规(半径与圆心)”工具,依次点选其中一条线段和F1,得到圆F1;再使用该工具,依次点选另外一条线段和F2,得到圆F2.调整点C的位置,使得得到的两圆有两个交点,使用“交点”工具描绘出这两个交点,再使用“轨迹”工具,依次点选其中一个交点和点C,得到这个交点的轨迹,使用同样的方法得到另外一个交点的轨迹,这样就得到了所求的轨迹——椭圆;
(5) 研究离心率e对椭圆形状的影响.
(为了观察方便,隐藏一些无关的图形因素)拖动滑动条,改变e的大小,观察e对椭圆形状的影响.拖动焦点F1的位置,观察椭圆形状的变化.(如图2所示)
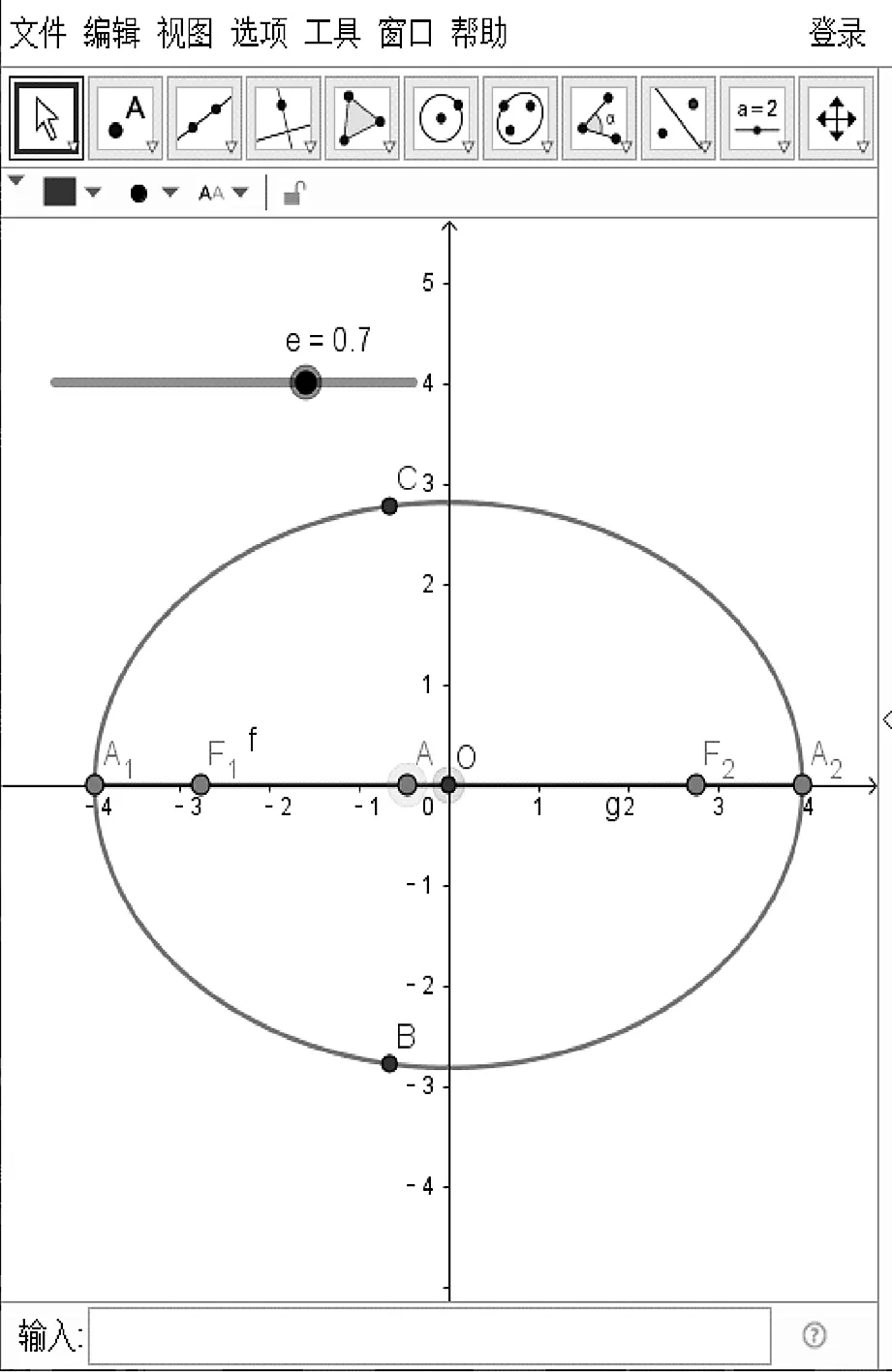
图2
案例3圆锥曲线的统一定义
抛物线是到定点F和定直线l的距离之比e=1的点P的轨迹.这不禁使人思考:当这个比值e(e>0)是一个不等于1的常数时,动点P的轨迹又是什么曲线呢?
教学分析:和案例1一样,可以先通过实验观察,猜想出轨迹,再进行严格的逻辑证明.
具体操作:
(1) 创建滑动条,定义参数e,并调整参数e的变化范围;
(2) 使用“描点”工具和“直线”工具作出定点F和直线l;
(3) 依次点选点P和直线l使用“垂线”工具得到垂线PA,垂足为A,使用“线段”工具作出线段PA;
(4) 在输入框内输入:D=(A+e*P)/(1+e),绘制点D,则点D为线段PA的定比分点;
(5) 依次点选点D,点A,使用“圆(圆心与一点)”工具绘制圆D,使用“对象上的点”工具在圆上作出的动点E;
(6) 连接线段DE,使用“直线”工具作出直线PE与直线l交于点G,点选点G,作出直线l的垂线k;
(7) 依次点选F和线段DE,使用“平行线”工具作出直线f,与直线k交于点P;
(8) 使用“轨迹”工具,依次点选点P和点E,得到点P的轨迹,(为了观察方便,隐藏一些无关的图形因素)拖动滑动条,改变e的大小,观察轨迹的变化.
由实验结果,我们可以对圆锥曲线下一个统一的定义:
任意给定常数e(e>0)、点F和直线l(F∉l),设动点P到F的距离与到直线l的距离之比等于e,则P的轨迹是圆锥曲线(不包括圆),其中F是这条圆锥曲线的焦点,l称为它的准线.
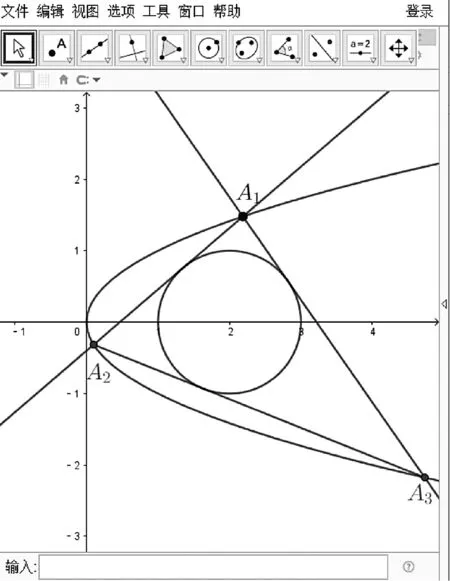
当0 当e>1时,P的轨迹是双曲线; 当e=1时,P的轨迹是抛物线. 图3 很多圆锥曲线试题蕴含丰富的性质,运用GeoGebra软件对这类题目进行探索和拓展,可以帮助学生认识和把握数学问题的实质, 发展直观想象与数学建模的学科素养. 案例4抛物线C的顶点为坐标原点O.焦点在x轴上,直线l:x=1交C于P,Q两点,且OP⊥OQ.已知点M(2,0),且⊙M与l相切. (1) 求C,⊙M的方程; (2) 设A1,A2,A3是C上的三个点,直线A1A2,A1A3均与⊙M相切.判断直线A2A3与⊙M的位置关系,并说明理由. 教学分析:根据题意容易得出抛物线C的方程为y2=x,⊙M的方程为(x-2)2+y2=1(过程略).下面利用GeoGebra软件来探究第二问.利用Geogebra在抛物线C作出动点A1,再运用“切线”命令作出⊙M的两条切线,即可发现直线A2A3与⊙M的位置关系. 具体操作: (1) 在输入框内输入:y^2=x,绘制抛物线C,输入:(x-2)^2+y^2=1,绘制⊙M; (2) 选择抛物线C,使用“对象上的点”工具在抛物线C上作出动点A1.选择点A1和⊙M,运用“切线”命令作出⊙M的两条切线,与抛物线C的两个交点为A2,A3,并选取点A2,A3作出直线A2A3; (3) 拖动A1点,可以发现当A1A2⊥x轴时,不满足题意,其余位置直线A2A3与⊙M保持相切.如图4所示. 图4 通过观察可以得出直线A2A3与⊙M相切的结论.下面还需要进行代数的证明.从点A1引出圆的两条切线,可以通过引入点A2,A3坐标,求出直线AB,AC的方程,再利用直线与圆相切这一条件构造出两个同构方程,进而解决问题. 代数证明: 设A1(x1y1),A2(x2,y2),A3(x3,y3),则y1,y2,y3两两互不相等. 直线A1A2的方程为:(y-y1)(x2-x1)=(x-x1)(y2-y1). 整理得:x-(y1+y2)y+y1y2=0. 同理直线A1A3的方程为x-(y1+y3)y+y1y3=0. 直线A2A3的方程为x-(y2+y3)y+y2y3=0. 所以圆心M到直线A2A3的距离 所以直线A2A3与圆M相切. GeoGebra软件能在课堂上更好地促进师生互动交流,也进一步提高了学生学习数学的兴趣.软件凭借其强大的功能,使学生产生探究知识的驱动力,为解析几何的教与学提供了新的路径,也为学生的解题提供新的思路,让学生可以轻松地在数学海洋里畅爽遨游,这必然对提高学生的学科素养大有裨益.
1.3 试题探究

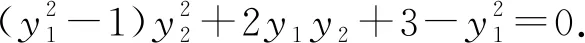
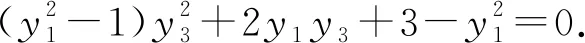

2 结束语

