基于TUCKER-DBN的机械故障识别方法研究

曾卉露，李志农,*，章熙琴，陈玉成，陶俊勇

（1.无损检测技术教育部重点实验室（南昌航空大学），南昌 330063；2.国防科技大学装备综合保障技术重点实验室，长沙 410073）

0 引言

深度学习由于在数据处理方面具有良好的迁移学习能力，被广泛应用于数据的处理分类及预测。其中，深度信念网络（Deep Belief Network，DBN）方法能够训练神经元间的权重，让神经网络生成训练数据，有利于识别和分类。在滚动轴承的故障诊断中DBN也进行了广泛的应用研究。沈涛等[1]综述了几种典型的深度学习模型，总结了DBN模型在故障诊断应用中的优缺点；Samanta等[2]将这一方法运用在对机器故障的检测中，但存在耗时长、迭代次数多等问题；Sanz等[3]结合深度学习与小波变换2种方法，先提取特征，再进行分类识别；熊景鸣等[4]结合DBN与粒子群优化支持向量机（PSO-SVM），提出了新型的滚动轴承故障诊断方法，提高了诊断准确率；Shao等[5]采用了深度信念网络进行了轴承故障检测的实验，结果表明，DBN能提高鲁棒性。

然而，现阶段对于DBN的研究仅停留在一维检测信号上，并没有将其优势扩大至更高维的情况。而实际工程应用中，故障信号产生往往被多个因素共同影响，并不是单一的信号。考虑到多个因素的影响会使得故障分类精度变高，而传统方法在复杂高维数据的特征提取过程中会产生误差，进而影响后续的故障诊断，张量TUCKER分解方法很好地解决了上述问题。许多学者对TUCKER分解进行了深入的研究。许小伟等[6]基于TUCKER分解设计了一种联立分解算法，对发动机故障进行了高效诊断；赵洪山等[7-8]提出了一种基于TUCKER分解的配电网数据的压缩方法，并与奇异值分解法进行比较；王东方等[9]利用TUCKER分解实现了更有效的彩色图像压缩，有效减少了图像信息损失。

为了能更好地解决传统故障识别过程中数据处理复杂、耗时长、识别准确率低的问题，本研究提出了TUCKER-DBN故障诊断方法，该方法通过对采集信号重构之后的模型进行TUCKER分解，将所得分解结果即核心张量作为DBN的输入，进行故障类型的分类。

1 原理分析

1.1 TUCKER分解

假 设 有 三 线 性 数 据 阵X,X∈RI×J×K，由TUCKER分解之后得到的三阶数据阵为G 。求解式‖X-G×U1×U2×U3‖，得到 最匹配 的优解 是TUCKER分解的主要目的。而得到最适配的解可以转化为式（1）中的最大值。

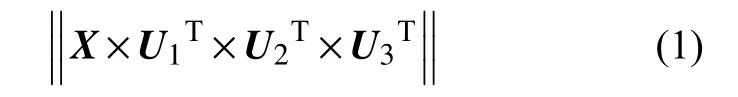
其中：U1∈RI×L,U2∈RJ×M,U3∈RK×N，L≤I,M≤J,N≤K 。

矩阵形式为：

因 子 矩 阵U1、U2、U3代 表 的 是X(1)、X(2)、X(3)的前L、M、N个左奇异向量构成的矩阵。算法的具体步骤如下：

1）若三线性数据阵X 的阶数R(n)满 足n≤3，则需要对数据阵X进行处理，即模-n矩阵化。处理之后可以得到X(n)。对矩阵X(n)按照式（3）进行奇异值分解。

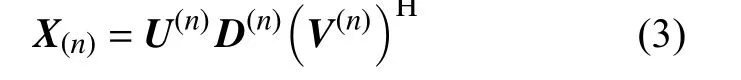
把U(n)的前R(n)个 列向量赋值给新的矩阵u(n)，然后使n=n+1，不断重复这一过程，直到当n＞3时为止。

2）当n＞3时，计算核心张量：

输出投影矩阵u(n)。

《政策》从区域、客户和项目三个维度明确了重点支持对象，为农行支持农业供给侧结构性改革、优化“三农”信贷结构指明了方向。在区域方面，重点支持茶叶特色农产品优势区、全国茶叶重点区域基地县、全国重点产茶县等茶叶特色明显的地区。在客户方面，特别强调加大对茶叶种植大户、专业合作社、农业产业化龙头企业等新型农业经营主体的支持力度。在项目方面，明确重点支持优质茶企开展低产茶园改造、生态茶园以及茶旅融合等项目建设。此外，《政策》还结合种植、加工、流通等各环节主体生产经营和资金需求特点，针对种植农户、经纪人、农民专业合作社、种植加工企业等茶产业链上的各类基础客户群体，分别制定了差异化的客户准入标准和支持政策。

3）判断其是否收敛。若收敛，则可根据式（4）计算核心张量，计算重构后的张量：

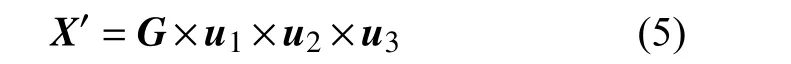
如果不收敛，则进行步骤4。

4）若n＞3，则上述步骤中求得的张量G为输出项。若n仍≤3，则进一步按照式（6）计算。解得不包含矩阵u(n)的所有矩阵：

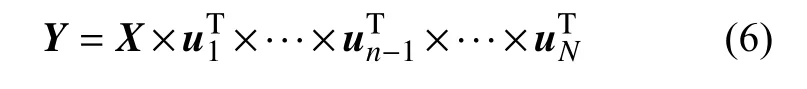
将Y(n)的前 R(n)个 左奇异值赋给u(n)。

5）重复步骤4，当n＞3时退出循环。

经过TUCKER分解后，能够得到一个核心张量。这一核心张量用G来表示。之后的步骤就是将核心张量G作为输入，输入到DBN分类器中去，进行DBN训练和分类。

1.2 DBN算法

DBN的优势在于能够训练其神经元，使其按照最大概率生成数据。DBN包含多层神经元，分为显性与隐性两部分。显性作用是接收输入数据，隐性作用就是进行数据的特征提取。DBN是由很多受限玻尔兹曼机（Restricted Boltzmann Machine，RBM）共同构成。RBM结构如图1所示。

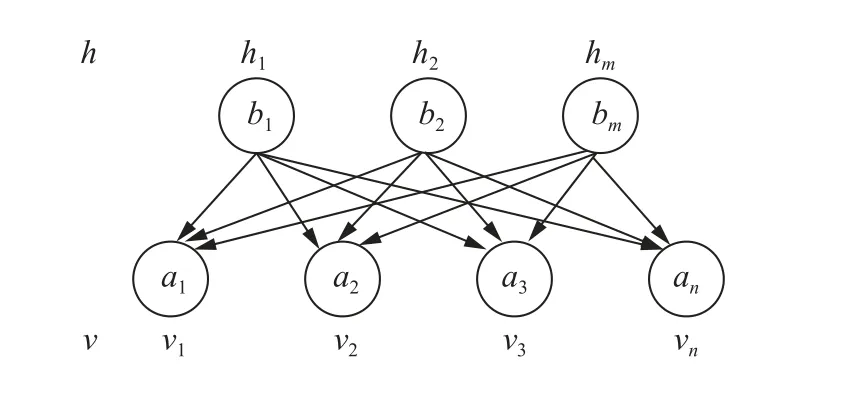
图1 RBM结构图Fig.1 RBM structure diagram

RBM结构中包含有多层神经元，被分为显元（即可视层神经元）与隐元（即隐藏层神经元）。令v=(v1,v2,···,vn)表示可视层神经元当前所处状态的向量；h=(h1,h2,···,hn)表示隐藏层神经元当前所处状态的向量；i表示可视节点单元，i∈[1,n]；j表示隐藏节点单元，j∈[1,m]。则对于任意的i、j，定义RBM的能量函数[10-12]为：

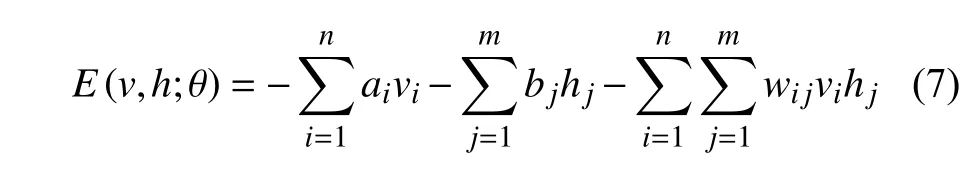
其中：a、b分别表示RBM中可视单元、隐藏单元的偏置；wij为连接的2个节点之间的权重值；θ={w,a,b}为参数。神经元有2个状态，分别是已激活和未激活。通常情况下，1表示已经激活，0表示还未激活。无论是可视层的神经元还是隐藏层的神经元，都只能属于0～1的集合中。

此时，该模型2个层的节点联合概率[13]可以按式（8）计算得出。

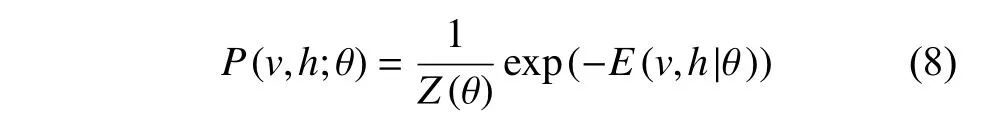
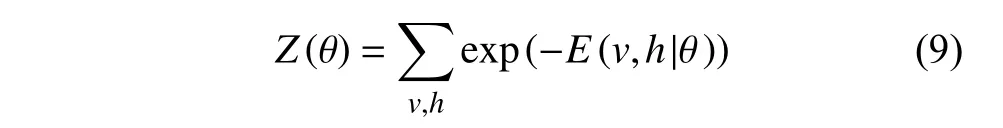
可视层条件概率：

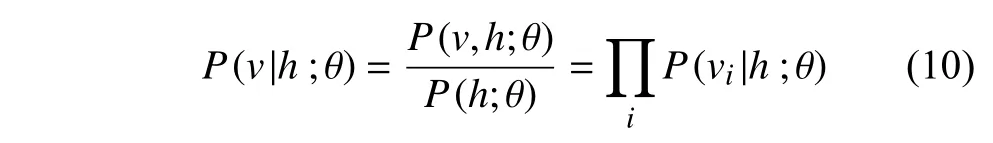
隐藏层条件概率：

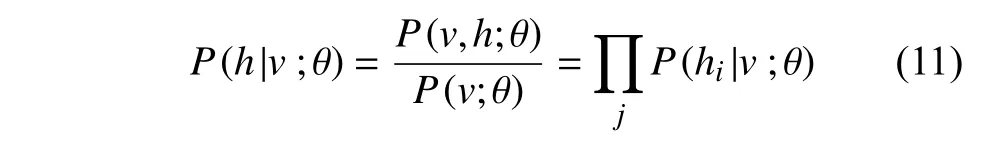
同一节点之间相互独立，可见层节点被激活时的概率为：

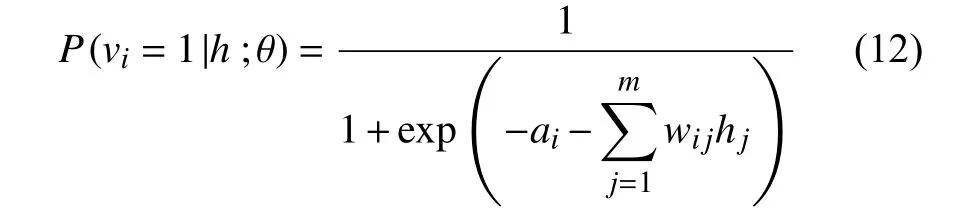
隐藏层节点被激活时的概率为：

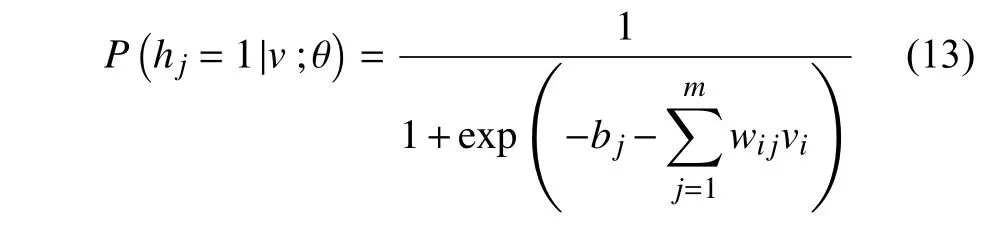
因为各个样本之间互不影响，所以可以利用最大化似然函数的求解寻找合适的参数。似然函数可以表示为：

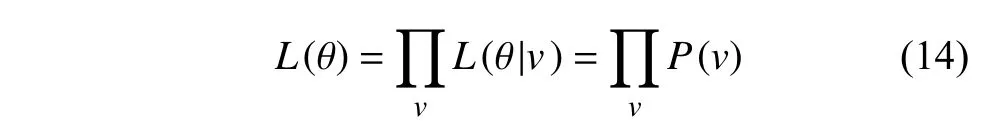
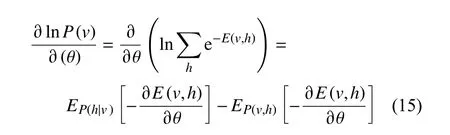
式中：P(v)表示可视层概率，θ表示RBM中的参数， E(v,h)表示能量函数。

所有的参数更新标准为：

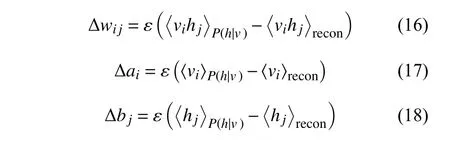
2 TUCKER-DBN模型建立

TUCKER分解的目的是为了得到张量G。G为核心张量，与原本张量不同，它是利用原本张量分解后压缩而成的新张量。这一方法得到的数据量远小于原始数据量，能够做到大幅度的数据压缩，因此非常利于数据处理。结合TUCKER分解和DBN，建立的TUCKER-DBN模型的算法如图2所示。

本研究选用发动机信号。选取部分状态与信号对发动机状态构建所需的三阶张量X ，X属于RI×J×K。张量分解后3个方向I、J、K分别代表发动机状态参数、曲轴转角以及转速。Xijk（i∈I,j∈J,k∈K）描述了转速为k、转角度为j时的第i种信号。

建立起对应的TUCKER-DBN模型之后，具体的执行过程如图2所示。在对原始数据进行归一化之后，先进行TUCKER分解，之后利用DBN进行训练和分类识别。

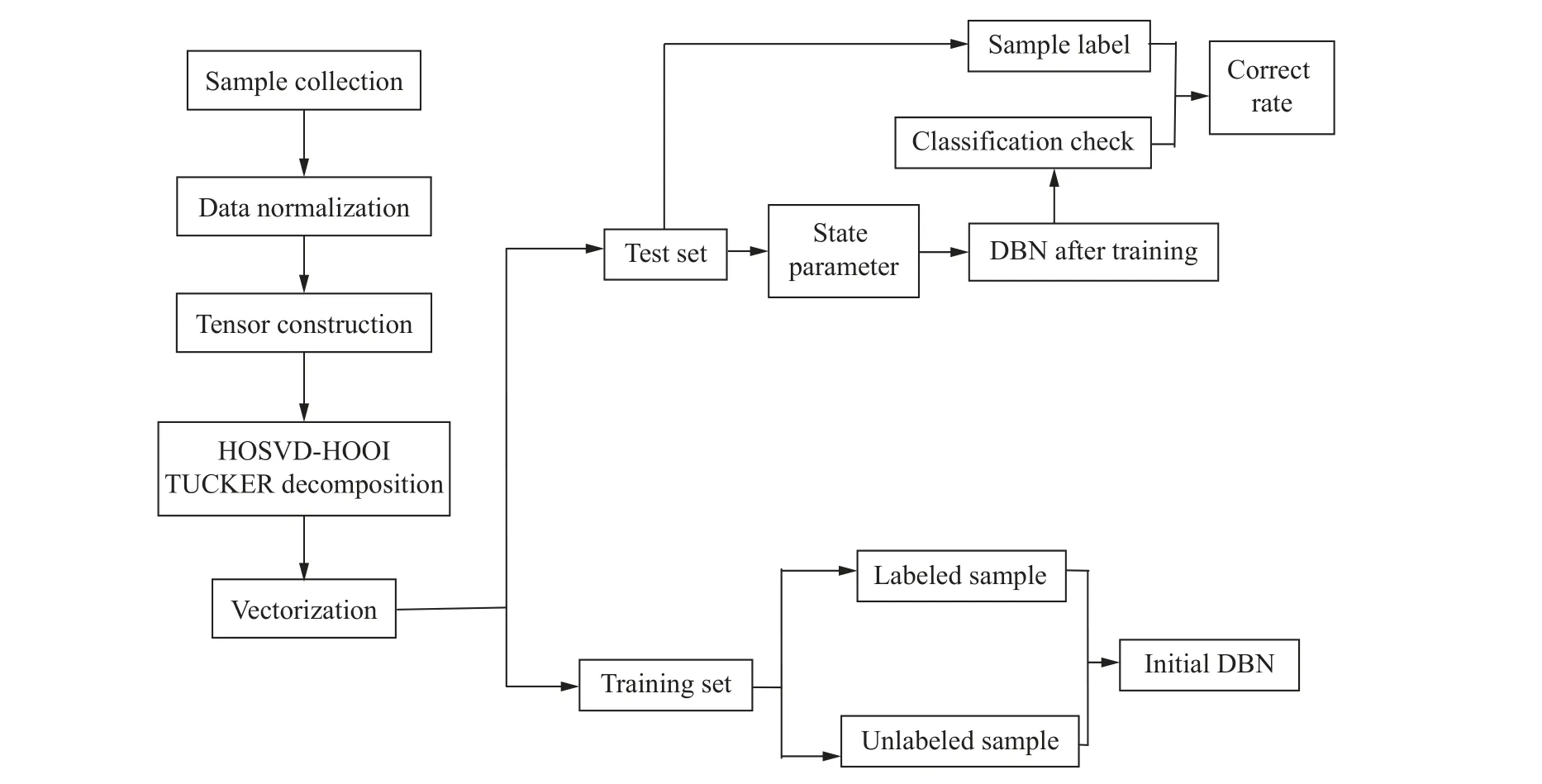
图2 TUCKER-DBN算法流程图Fig.2 TUCKER-DBN algorithm flow chart

3 实验研究

选用康明斯4B3.9-G2型发动机的参数作为依照，在GT-Crank软件中搭建虚拟样机进行验证。发动机转速为1500 r/min时开始采集，分别采集发动机正常状态下、发动机单缸失火状态下、发动机轴系不对中状态下的数据作为实验样本。

实验中构建三阶张量的第1阶表示的是发动机的状态参数。本实验中共有状态参数分别为：曲柄销处的连杆力、曲轴端转矩、连杆轴向力、飞轮惯性力矩4项随曲轴转角的变化关系，所以第1阶维数为4。第2阶表示的是收集数据的次数。由于曲轴转角考虑范围是0°～180°，每转1°采集一次，共收集180次数据，因此第二阶维数为180。发动机开始时转速为1500 r/min，最终转速为3000 r/min，每增加50 r/min采集一次数据，共能够采集到31组数据，则第3阶维数为31。由此，实验数据构成4×180×31的三阶数据阵。

实验进行了120次，其中，30次样本用作测试样本，另90次样本作为训练样本。实验一共采集到4×31×120个长度为180的数据。由于实验考虑了多个故障因素，所以选用Sofmax分类器进行故障分类。本研究中分别使用0、1、2表示发动机正常、单缸失火、轴系不对中的3种状态，并记录如表1所示。

表 1实验数据说明Table 1 Detail of experiments

图3为未进行和进行TUCKER分解后进行DBN分类的故障分类识别率统计。比较图3a、图3b可以看出：未使用TUCKER分解时，其识别率为85%～95%，而使用了TUCKER分解之后，识别率为90%～100%。由此可知，使用TUCKER分解可以提高故障分类识别的准确率。

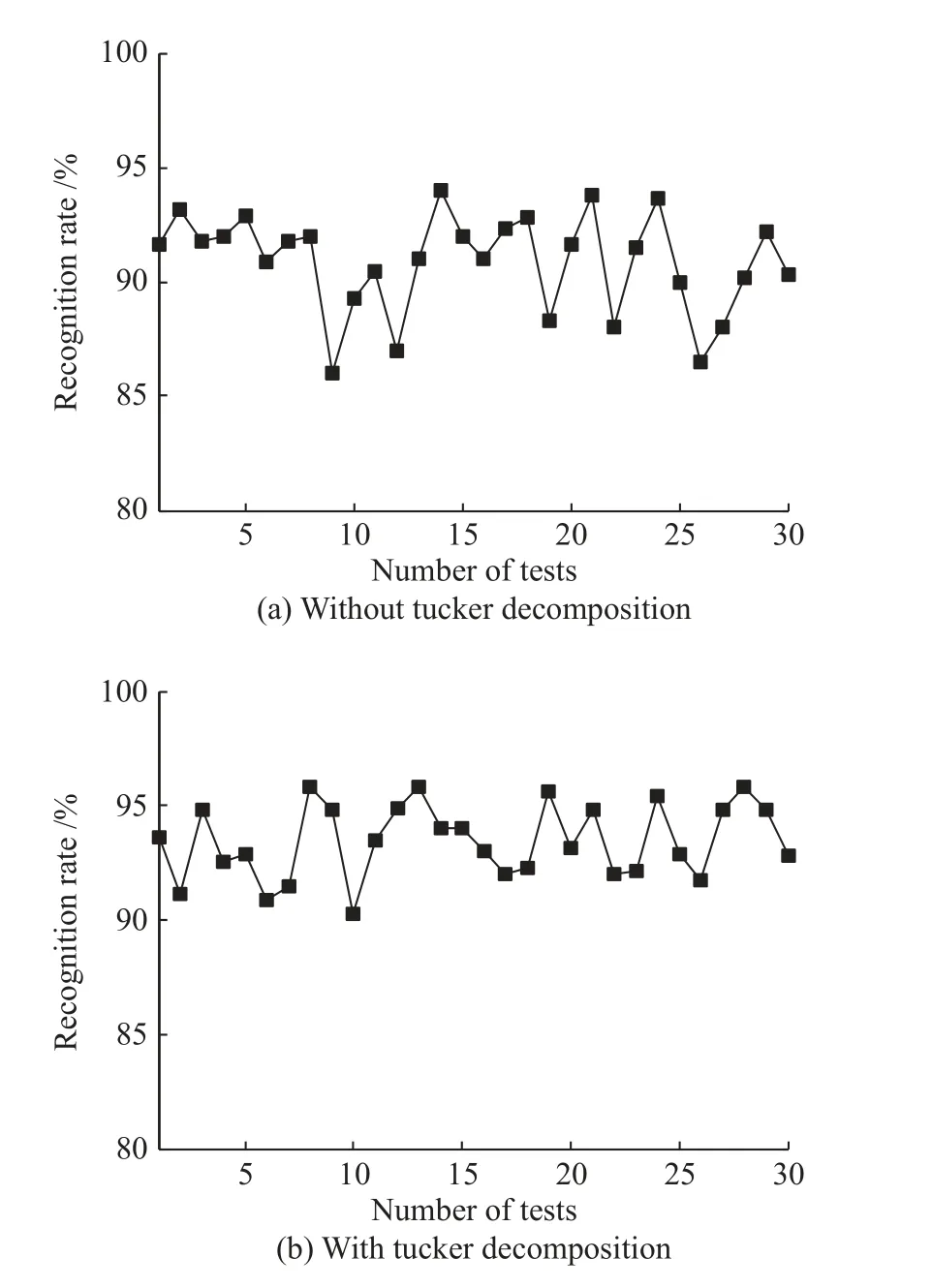
图3 故障分类正确识别率Fig.3 Correct recognition rate of fault classification

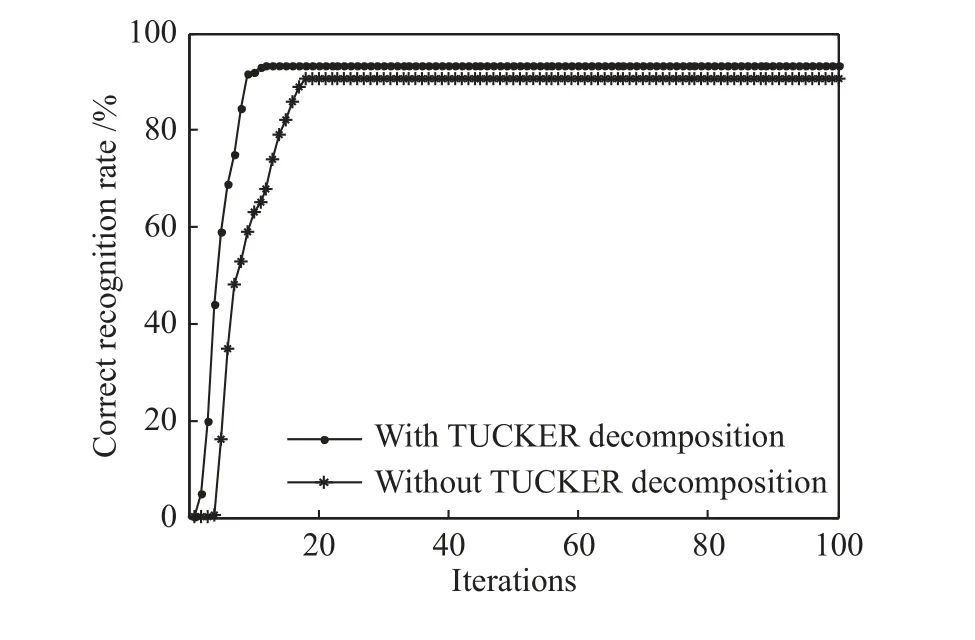
图4识别率与迭代次数Fig.4 Recognition rateand iteration times

图4 为使用和未使用TUCKER分解的识别率与迭代次数的关系曲线。由图4可知，使用TUCKER分解较未使用TUCKER分解的正确识别率更高；使用TUCKER分解所需的迭代次数更少，所需的训练时间相对较短，即效率更高。实验结果如表2所示。由此可知，利用TUCKER分解可以用较少的迭代次数实现较高的识别率。因此，TUCKERDBN识别方法具有一定优势。

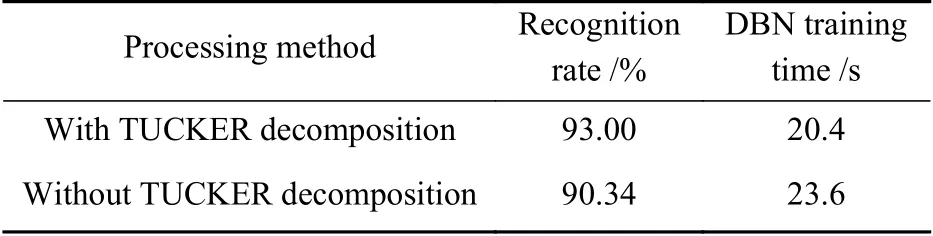
表2 实验结果对比Table 2 Comparison of experimental results

实验采集了3种不同状态下的发动机数据样本，对于每种类型的故障，分别选用10组数据进行测试，测试结果如图5所示。可见有2个测试样本出现错误分类的情况，分别是4、19号样本没有被归类于类别2。类别2即轴系没有对中而产生的故障。通过基于TUCKER分解的深度信念网络识别算法，大部分的测试结果都被正确识别。本次测试样本容量为30，28个样本被正确识别分类，识别率为93%。说明了该方法的正确识别率较高。

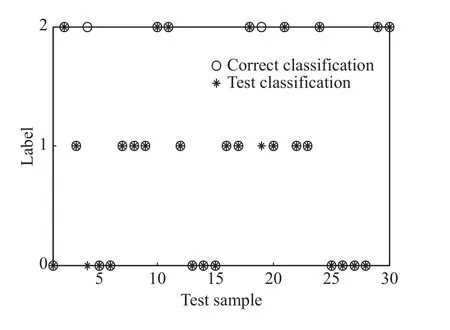
图5 测试样本标签分类Fig.5 Label classification of test

4 结论

1）提出了一种利用TUCKER分解大幅度压缩数据，再提取其核心张量作为故障特征，将核心张量输入到DBN分类器中进行训练和识别的深度信念网络算法。

3）在采集的120个样本中，选择30个样本进行故障识别测试实验，使用TUCKER-DBN识别方法的识别率为93%，验证了所提方法应用于发动机故障识别具有一定的可靠性。

2）与未使用TUCKER分解相对比，使用TUCKER分解的有效识别率更高，迭代次数更少，训练时间更短。