高考函数零点问题解题策略透视
——从一道课本“函数零点”题谈起
安徽省太湖中学(246400) 李昭平
1 引例与解析
题目(新人教A 版选择性必修第二册第104 页第19 题)设a ∈R,函数f(x)=ae2x+(a −2)ex −x.
(1)讨论f(x)的单调性;(2)若f(x)有两个零点,求a的取值范围.
分析本题是一道章节复习题,是指数函数与一次函数的复合型函数,综合考查导数在函数的单调性、极值、零点、图象等问题中的应用,很好体现了分类讨论、数形结合、极限思想、特殊化思想、方程思想、等价转化等数学思想方法.第(1)问是常见类型,通过讨论参数a,确定导函数f′(x)的符号,得到单调性.第(2)问则是含参数的函数f(x)的零点问题,有多种解题思路.通过探究得到下述两种解答.
解答(1)当a≤0 时,f(x)在R 内单调递减;当a >0时,f(x)在(−∞,−lna)内单调递减,在(−lna,+∞)内单调递增.解答过程略去.以下讨论第(2)问的解答.
解法1(图象法)f′(x)=2ae2x+(a −2)ex −1=(aex −1)(2ex+1)=0.当a≤0 时,f′(x)<0,函数单调递减,最多一个零点,不合题意,舍去.当a>0 时,由f′(x)=0得到aex −1=0,x=−lna.f(−lna) 是极小值,必须f(−lna)<0,即lna −

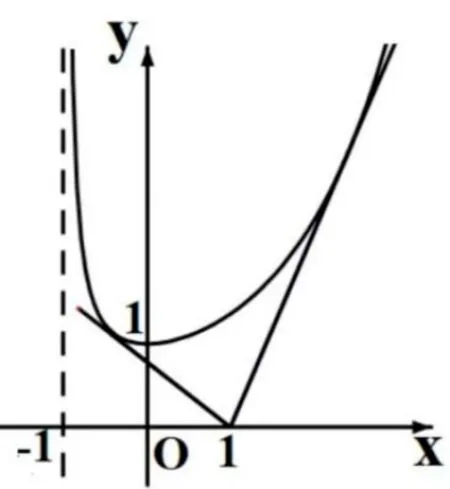
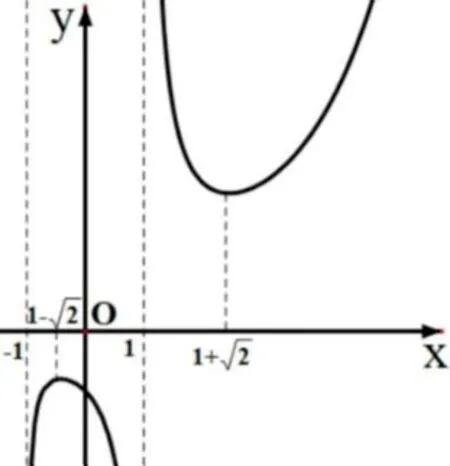
当x >0 时,g′(x)<0,g(x)单调递减,且g(x)>0.当x <0 时,g′(x)>0,g(x) 单调递增,且g(−1)<0.g(0)=1 是其极大值,也是最大值.如图1 可知,当0 图1 点评这种解法,先由f(x)=0 参变分离得到关键要画出新函数g(x) 的图象草图,难点在于对g′(x)的分子进行因式分解,找g′(x)的零点和判断g′(x)的符号,需要较高的运算和变形技巧. 对于含参数的函数零点问题,一般有以下策略,其中的φ(x)可以是函数f(x)或f′(x)或f′′(x)等等. 策略1(图象法)研究函数φ(x)的零点,先利用导数研究其大致图象,再看图象与横轴的交点情况,数形结合处理问题. 策略2(参变分离•构造函数法)研究函数φ(x)的零点,先将φ(x)=0 变为a=g(x),其中a为参数,再看曲线y=g(x)和直线y=a的交点情况,数形结合处理问题. 策略3(一分为二•构造函数•图象交点法)研究函数φ(x) 的零点,设φ(x)=g(x)−h(x) 将φ(x)=0“一分为二”变成g(x)=h(x)再看曲线y=g(x)和曲线y=h(x)的交点情况,数形结合处理问题. 显然,上题是利用策略1 和策略2.根据本题的结构特征,利用策略3(一分为二•构造函数•图象交点法)比较困难.这给我们的启示是,解题中往往按照上述三种路径去思考,但要选择最优化的思路,快速顺利实现解题目标. 当a≥0 时,两函数的图象在x ∈[1,e]上只有一个公共点,不合题意.当a <0 时,如图2,直线h(x)=−a(x−1)极限位置是曲线g(x)=xlnx在点(1,0)处的切线y=x −1.因此−a >1,且g(e) ≥h(e),解得≤a <−1.故选A. 图2 点评本题考查f(x)的零点,利用策略3,“一分为二”成两个函数g(x)=xlnx(定曲线)和h(x)=−a(x −1)(动直线),则问题立即转化为定曲线与动直线的位置关系.数形结合、动静变化、极限位置,注意对参数a的分类讨论和不等式g(e)≥h(e)中等号能取到. 点评本题以幂函数和指数函数的复合形式为载体,考查零点的存在性问题,利用策略1 先确定极值和大致图象,融函数的单调性、分类讨论、数形结合、放缩等知识于一体,有一定的难度.在“找点”中,运用了不等式ex >x2(x >0)进行放缩. 例3 (2022 年皖江联盟联考题) 已知函数f(x)=ln(1+x)+axe−x,a ∈R. (1) 若 曲 线y=f(x) 在点(0,f(0)) 处的切线方程是y=2x,求a的值; (2)若f(x)的导函数f′(x)恰有两个零点,求a的取值范围. 图3 解 析(1) 因 为f′(x)=+a(1−x)e−x,所 以f′(0)=1 +a.因为曲线y=f(x) 在点(0,f(0)) 处的切线方程是y=2x,所以f′(0)=2.于是1 +a=2,故a=1.以下考虑(2)的解答. 点评本道联考题实际上是2022 年全国高考数学乙卷第21 题的改编,将原高考题中的条件“f(x)恰有两个零点”变为“导函数f′(x)恰有两个零点”,思路和解法跟高考题类似,但运算量明显增大,属于较难题.解法1 是利用策略3,解法2 是利用策略2,都不易. 将例3 的函数f(x)=ln(1+x)+axe−x中的参数a变换位置为f(x)=aln(1+x)+xe−x,类比引申则得到: 变式题已知函数f(x)=aln(1+x)+xe−x,a ∈R. (1) 若曲线y=f(x) 在点(0,f(0)) 处的切线方程是y=2x,求a的值; (2)若f(x)的导函数f′(x)恰有两个零点,求a的取值范围. 解析(1) 因为f′(x)=+(1−x)e−x,所以f′(0)=1+a.因为曲线y=f(x) 在点(0,f(0)) 处的切线方程是y=2x,所以f′(0)=2.于是1+a=2,故a=1. 图4 图5 例4(2022 年江西南昌市模考题) 已知函数f(x)=ex+acosx,其中x>0,a ∈R. (1)当a=−1 时,讨论f(x)的单调性; (2)若函数f(x)的导函数f′(x)在(0,π)内有且仅有一个极值点,求a的取值范围. 解析(1)易得函数f(x)在(0,+∞)内单调递增,过程略去. 图6 以上我们从一道课本题出发,通过分析、解答,归纳出解函数零点问题的三种策略.再通过三种运用,强化对策略的认识与理解.在整个过程中,融观察分析、直觉逻辑、提炼概括、运用升华于一体.这给我们的启示是: 对一道好的课本题进行多方向、多侧面、多角度研究,应用到课堂上,必能收获丰盈.
2 结论及其应用
2.1 应用于函数f(x)的零点问题



2.2 应用于函数f′(x)的零点问题




2.3 应用于函数f′′(x)的零点问题




