一道解析几何试题的探究与拓展
广东省河源市龙川县实验中学(517300) 陈国定

(1)求点N的轨迹方程C;
(2)设C与x轴交于点A,B(A在B的左侧),点M为C上一动点(且不与A,B重合),设直线AM,x轴与直线x=4 分别交于点R,S,取点E(1,0),连接ER,证明:ER为∠MES的角平分线.


评注以上三种解法从不同的角度解决问题,体现了数学思维的发散性、灵活性、探究性.解法1 以角平分线上的点到角两边的距离相等的角度为突破口展开求解,显然是通法,属于“舒适区”范围;解法2 以二倍角的正切公式为突破口展开求解.该想法也很自然,既然是角平分线,显然两个角是两倍关系,只要计算它们的斜率满足倍角公式即可,属于“最近发展区”范围;解法3 以角平分线的向量表示形式为突破口展开求解,该想法有点新颖,却也在“跳一跳、够得着”的新发现区范围内.当然,从向量夹角的角度去证明余弦值相等也是一种途径(证明略).题目虽然解答完毕,但探究还需继续.既然ER为∠REB平分线,同理可得ET为∠NEB平分线,所以∠RET为直角,那么该圆与直线MN相切于点E吗? 结论能否推广到一般情形呢? 对此,我们有如下的一般结论:
结论1 如图1,已知椭圆C:=1(a >b >0)的左、右顶点分别为A,B,右焦点为F,过F作直线l与椭圆交于点M,N两点,直线AM和直线AN分别交直线x=于点R和T,则有:

图1


这里笔者没有采用前面三种思路去证明FR,FT为角平分线,进而再去推导∠RFT为直角.而是通过联立方程组并借助韦达定理,进而算出向量的数量积为零或斜率积为−1 这一通性通法来证明该结论.运算量相对比较大,而且代数式中含有大量的字母,会使很多人望而却步.可解析几何最大的特点就是将几何问题坐标化,得到方程(组),再进行代数式的化简或变形运算来解决问题,所以运算能力是解决解析几何最核心、最基本的内功,更要细心、耐心地运算,跨过畏难怕算的心里障碍.
类似地,在双曲线和抛物线中也有相应的结论.
结论2 如图2,已知双曲线C:=1(a >b >0) 的左、右顶点分别为A,B,右焦点为F,过F作直线l与双曲线交于点M,N两点,直线AM和直线AN分别交直线x=(c2=a2+b2)于点R和T,则有:

图2
证明过程与椭圆类似,此处省略.
结论3 如图3,已知抛物线C:y2=2px的顶点和焦点分别为A,F,过F作直线l与抛物线交于点M,N两点,直线AM和直线AN分别交准线于点R和T,则有:
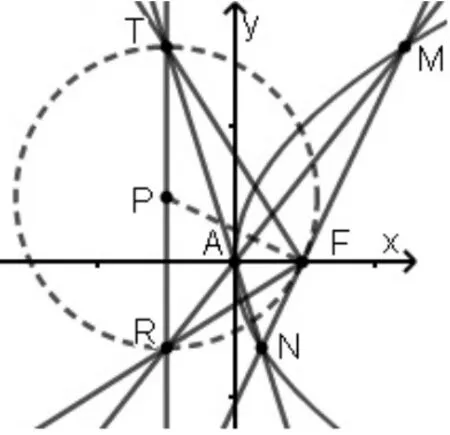
图3

所以PF⊥MN.命题得证.
至此,通过以上的推导,证明了椭圆、双曲线及抛物线都具有类似的性质.在探究过程中采用了由特殊到一般及类比的研究方法,这是数学发现的重要思想方法.著名数学教育家波利亚说过:“在你找到第一个蘑菇或作出第一个发现后,要环顾四周,因为它们总是成堆生长的”.所以,在平时的教学中,要对题目进行回顾与反思,积极引导学生去发现问题、提出问题、解决问题.尽量把题目进行探究与推广,从而达到会一道题到会一类题的效果,甚至探究到更一般的结论.这样不仅能激发学生的学习兴趣,还能培养学生形成积极主动,勇于探索的学习习惯,同时也能培养学生的创新意识.

