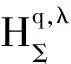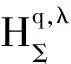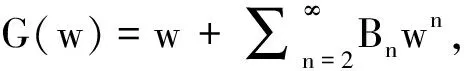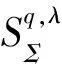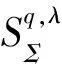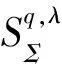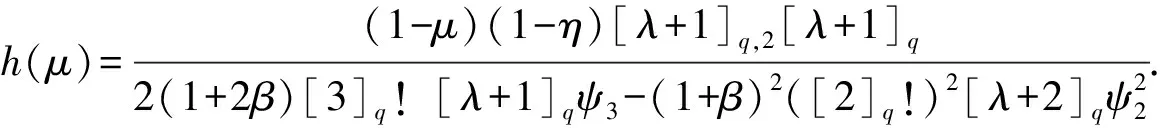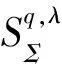与q-导数相关的双近于凸函数的Faber多项式系数估计
翟 杰, 程 莹, 刘金林
(扬州大学数学科学学院, 江苏 扬州 225002)

1 预备知识
设函数f,g∈T, 若存在Schwarz函数φ,φ(0)=0且|φ(z)|<1, 使得f(z)=g(φ(z)), 则称函数f从属于g, 记作f(z)g(z).特别地, 若g在Δ中单叶, 则f(z)g(z)⟺f(0)=g(0)且f(Δ)⊂g(Δ).


设-1≤B 注1[1]若令函数类S*(A,B),C(A,B)和K(A,B)中A=1-2α(0≤α<1)且B=-1,可得熟知的解析函数类S*(α),C(α)和K(α). 设0 (1) 设函数f∈S, 其反函数f-1满足f(f-1(w))=w(|w| (2) 和 和 (3) 因此, 根据Faber多项式展开可得 (4) (5) (6) 和 (7) (8) 当2≤k≤n-1时, 若ak=0和bk=0, 则 (9) 类似地, 通过式(5)和(7),可得 (10) 由假设条件有An=-an,则 (11) 注3在定理1中, 令A=1-2η(0≤η<1)且B=-1,可得文献[3]中的定理1. 经过仔细调查分析,专责小组当时获得一些基础数据。比如,患者在医院平均候诊时间是57分钟,上午候诊时间比下午长;患者的平均就诊时间为5分钟。而且,经过信息统计和诊室调查两相比对,专责小组摸清了每位医生的诊疗习惯,估算出不同医生平均接诊时间。 证明 令式(8)(10)中n=2,3,可得 (12) (13) (14) (15) 由式(12)和(14)并根据引理1,得 由式(13)和(15),得 从而 (16) 同样利用引理1和引理2,可得 (17) 将式(16)代入式(17)并利用引理1和引理2,有 并再次使用引理1和引理2,有 定理2证毕. 令定理2中A=1-2η(0≤η<1)且B=-1,可得以下推论. 证明 根据式(16)和(17),得 从而 (18) 定理3证毕. 在定理3中, 令A=1-2η(0≤η<1)且B=-1,有以下推论. 在定理3中, 令μ=1, 有以下推论.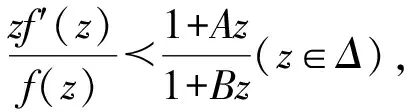











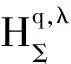
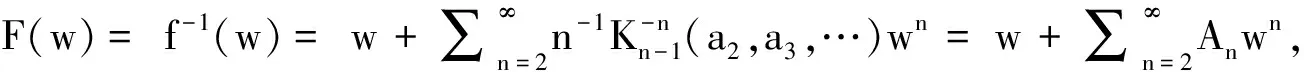



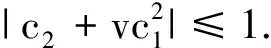
2 主要结果