一类二维桥式起重机系统的分层滑模控制

刘 忠, 温雨柔, 楼旭阳

(江南大学物联网工程学院, 江苏 无锡 214122)

桥式起重机是一种常用的搬运设备,作为非线性、欠驱动且强耦合的系统, 其安全高效的运行取决于有效的负载摆动抑制方法和实时跟踪控制理论[1]．针对桥式起重机负载摆动及跟踪控制的研究方法主要分为线性化模型和非线性模型两类,因前者对系统模型进行线性化处理降低了负载摆角等信息的准确性,导致系统的负载摆动过大和搬运位置出现偏差[2],故后者成为研究热点．Sun等[3]通过改进控制器的积分项有效抑制了负载摆动; Chen等[4]考虑起重机的驱动和欠驱动的状态约束问题,通过设计带有辅助信号的策略解决了起重机负载在搬运过程中的摆动及负载位置追踪问题．然而,在实际应用中,桥式起重机不可避免地经受各种干扰,系统性能大幅下降,故如何提高系统的抗扰能力备受关注．Wu等[5]通过设计扰动观测器在有限时间内抑制或消除不确定干扰; Zhang[6]提出有限时间追踪控制器, 使得系统在受外部干扰及模型参数不确定的情况下仍具良好的控制性能．滑模控制方法[7]则不受系统参数和外部扰动的影响,且鲁棒性好．Wu等[8]针对桥式起重机系统中不确定干扰,设计了连续全局滑模控制器和非线性干扰观测器,有效解决了干扰所致不利影响; Lu等[9]引入一种扰动设计观测器减轻了滑模控制系统固有的抖振问题, 使得桥式起重机能够估计并消除观测器的影响; Tuan等[10]针对起重机参数不确定的问题, 设计了二阶滑模控制器,使得系统在参数变化较大的情况下仍然保持良好的控制效果;梁慧慧等[11]在设计滑模面时引入积分项使得系统状态一直处于滑模面上; Sun等[12]提出一种滑模控制器有效解决了起重机在未建模不确定性下的防摆控制问题,但该控制方法需要预先构建系统状态轨迹并进行相应状态分析; Le等[13]结合鲁棒观测器与分层滑模控制，提高了系统的鲁棒性,但抑制负载摆动能力不突出．

为了抑制二维桥式起重机摆杆的振动以及快速实现起重机运送负载到达期望位置, 本文拟基于传统滑模控制器(conventional sliding mode control, CSMC), 通过两层滑模面的联合设计构建分层滑模控制器(hierarchical sliding mode control, HSMC), 并利用Lyapunov方法分别证明在CSMC和HSMC作用下闭环系统的稳定性．

1 问题描述

考虑如图1所示的欠驱动二维桥式起重机模型, 负载通过摆杆悬挂在电车底部, 其中M,m分别为电车和负载的质量,θ为负载的摆角,l为摆杆长度,x为电车所处位置,Fa为施加于电车的驱动力．因考虑负载质量, 故摆杆质量忽略不计．

图1 桥式起重机模型Fig.1 Structure of an overhead crane system

二维桥式起重机的动力学方程如下:

(1)

(2)

其中g为重力加速度.系统控制目标: 在控制力Fa的作用下, 负载从初始位置x0移动到设定位置xd, 并在整个运动过程中抑制负载摆角θ．

为了使后续的控制器设计过程更加简洁, 现将控制力Fa设计为如下形式:

(3)

其中u为待设计控制器．本文通过控制器u实现对整个桥式起重机运动的控制．

将式(3)代入式(1), 可得

(4)

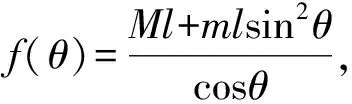
(5)

于是, 系统运动学方程等价为式(2)(5)．进一步地,整个系统变换成如下矩阵表达形式:

(6)

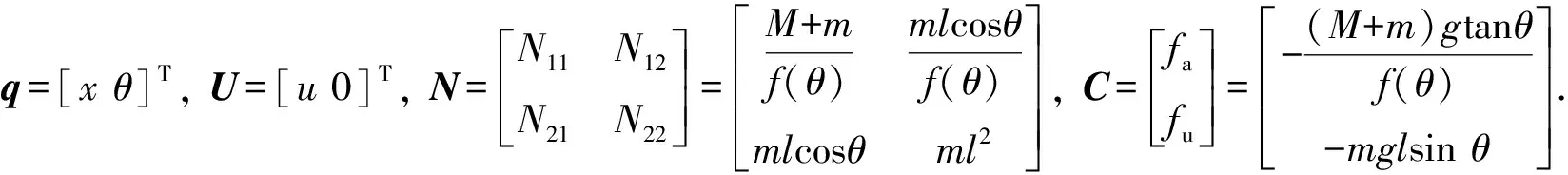
(7)

其中变量f1,f2,b1,b2分别为

(8)

(9)

2 传统滑模控制器设计及稳定性分析

定义传统滑模控制器的滑模面

(10)

其中c1,c2,c3均为常数．

(11)

下面考虑当系统(9)到达滑模面s=0时, 其状态(x1,x2,x3,x4)会沿滑模面趋向于点(0,0,0,0)．

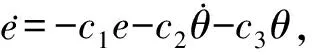
(12)

(13)

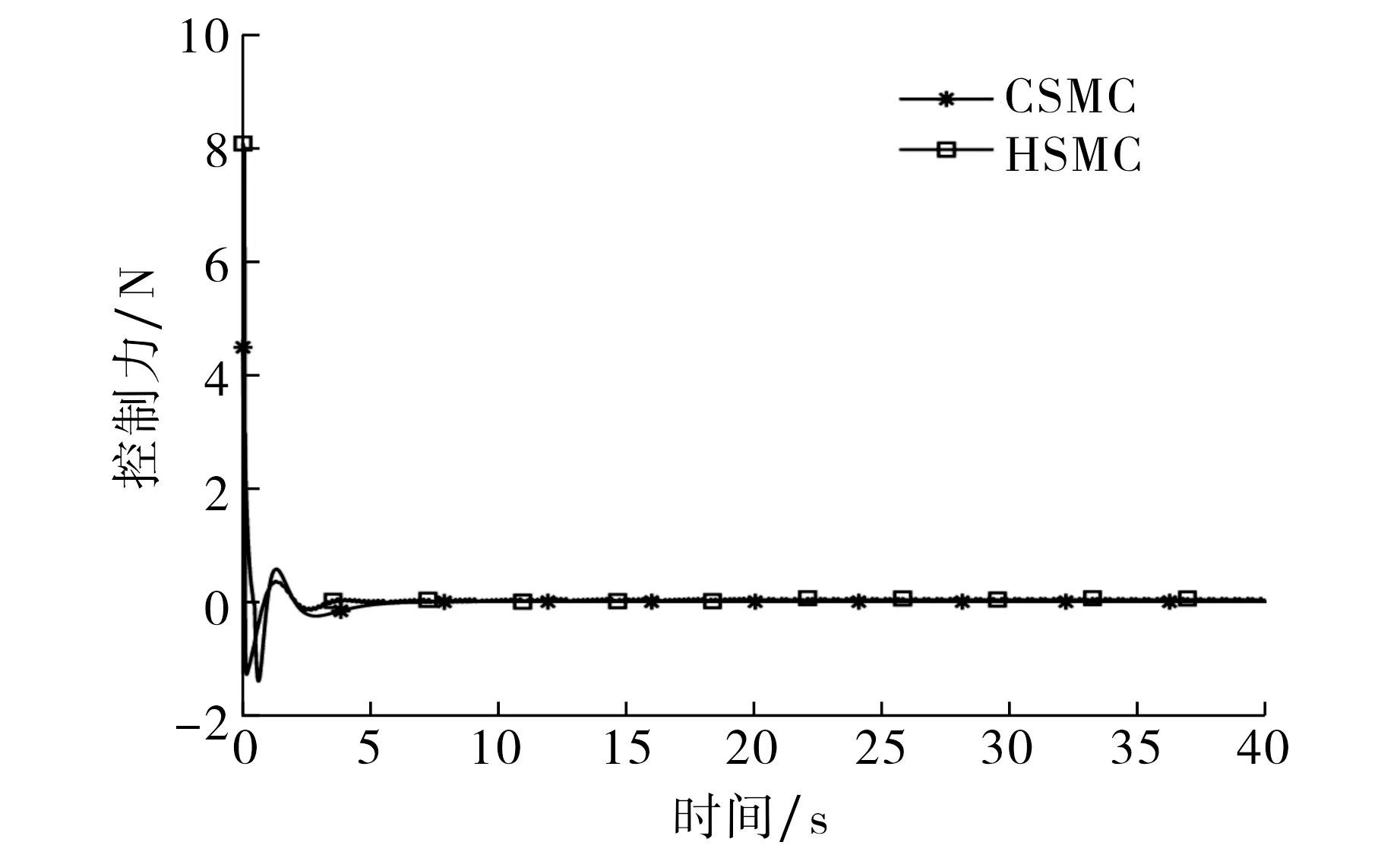
定理2考虑系统(13), 如果系统参数满足c1>0,c2

证明 已知平衡点(x1,x2,x3,x4)=(0,0,0,0)等价于(z1,z2,z3)=(0,0,0), 在平衡点处作线性化处理,则

(14)

其中εi(i=1,2,3)为线性化的偏差．式(14)可改写为

(15)

(16)

因此, 当常数c1,c2,c3满足条件(16)时, 系数矩阵A的特征值具有负实部, 这意味着线性系统(15)严格稳定, 从而非线性系统(14)在平衡点处渐近稳定,系统状态将沿滑模面运动至平衡点,即(x1,x2,x3,x4)→(0,0,0,0)．证毕．

3 分层滑模控制器设计及稳定性分析

首先,选取第一层滑模面:

(17)

(18)

(19)

ueq=ueq1+ueq2．

(20)

整个控制器由等效控制与切换控制组成, 令切换控制为usw, 则控制器

u=ueq+usw．

(21)

其次, 设计第二层滑模面

S=μ1s1+μ2s2,

(22)

(23)

将式(7)(20)代入式(23),得到切换控制

(24)

将式(20)(24)代入式(21),得到控制器

(25)

令w=supt≥0|ueq2-ueq1|, 且μ1,α满足如下条件:

(26)

定理3考虑系统(9), 若控制器(25)中参数满足条件(26), 则系统状态能在有限时间内分别到达第二层和第一层滑模面．

下面证明系统能在有限时间到达第一层滑模面．

(27)

令tr4=max{tr2,tr3}, 则当t=tr4时, 系统收敛至第二层滑模面S与第一层滑模面s1．由于s2=(S-μ1s1)/μ2, 所以系统在有限时间tr4到达第一层滑模面s2．证毕．

综上所述, 若满足条件(26), 系统状态将沿滑模面运动到平衡点, 即(x1,x2,x3,x4)→(0,0,0,0)．证毕．

4 数值仿真与实验分析

4.1 数值仿真

通过数值仿真验证本文所提出的分层滑模控制器(25)的有效性, 并与传统滑模控制器(11)、文献[12]中滑模控制器以及文献[13]中分层滑模控制器进行对比．

给定桥式起重机系统参数M=2 kg,m=0.8 kg,l=1.2 m, 重力加速度g=9.81 m·s-2．负载的设定位置xd=0.6 m．传统滑模控制器参数c1=0.45,c2=-9.1,c3=0.104,η=15, 分层滑模控制器参数k1=0.63,k2=8.3,μ1=1.9,μ20=1.1,α=15,β=50．

电车的位置轨迹及负载摆角变化如图2所示．由图2可见: 1) 在传统滑模控制器(11)和本文分层滑模控制器(25)分别作用下, 二维桥式起重机均能将负载迅速搬运至指定位置,并且在搬运过程中的负载摆角均能得到有效抑制; 2) 与文献[12-13]中提出的滑模控制器相比, 本文分层滑模控制器(25)能更快地将负载运送至期望位置并且有效抑制负载摆动．

传统滑模控制器与本文分层滑模控制器的滑模面轨迹如图3所示．由图3可见: 由于CSMC设计的趋近常数取值较大, 故传统滑模控制作用下滑模面收敛更快．

图2 4种滑模控制器下的电车位置轨迹(a)和负载摆角(b)Fig.2 Trolley position track (a) and swing angle (b) under four sliding mode controllers

图3 CSMC(a)与HSMC(b)的滑模面轨迹Fig.3 The sliding mode surface trajectories of CSMC (a) and HSMC (b)

为了降低滑模抖振的影响, 在数值仿真时采用饱和函数代替控制器中的符号函数, 传统滑模控制与本文分层滑模控制作用下的控制力如图4所示．由图4可见: 本文分层滑模控制器(25)的控制效果虽优于传统滑模控制器(11), 但其代价是控制力的波动较大．

4.2 实物实验

在如图5所示的桥式起重机实验平台对传统滑模控制器和本文分层滑模控制器进行实物验证．该实验平台中主控芯片为意法半导体公司的STM32F03CT6单片机, 驱动器为松下MADLT05SF, 伺服电机为松下MSMF012L1UM．实验平台的参数M=2.1 kg,m=9.4 kg,l=1 m．给定电车初始位置x0=0.1 m, 设定位置xd=0.5 m, 传统滑模控制器的参数c1=0.9,c2=-0.04,c3=0.05,η=2.4, 分层滑模控制的参数k1=0.85,k2=9.4,μ1=1.8,μ20=1.1,α=20,β=50．

图4 CSMC与HSMC下的控制力Fig.4 Control force under CSMC and HSMC

图5 实验平台Fig.5 Experimental platform

电车在电动机牵引下的位置轨迹如图6所示．由图6可知: 1) 本文分层滑模控制器(25)能更快地将负载搬运至设定位置; 2) 搬运负载过程中,传统滑模控制器(11)作用下的负载摆角幅值较小; 3) 当负载到达设定位置后, 在控制器(11)(25)分别作用下的负载摆角都是逐渐收敛的; 4) 综合考虑负载摆角和搬运效率,分层滑模控制器(25)因通过联合2个滑模面来设计控制器, 故其控制效果更优．

图6 实验平台中CSMC与HSMC作用下的电车位置轨迹(a)与负载摆角(b)Fig.6 Trolley position (a) and swing angle (b) under CSMC and HSMC in experiment

图7 实验平台中CSMC与HSMC下的控制力Fig.7 Control force of the CSMC and HSMC under experimental platform

传统滑模控制与本文分层滑模控制作用下的控制力如图7所示．由图7可知: 传统滑模控制器作用下控制信号存在频繁切换现象, 若长时间运行将导致实际执行器损坏; 本文分层滑模控制器作用下控制信号相对平滑,更具实用性．

5 结语

本文针对桥式起重机在搬运负载过程中存在的负载摆动及位置跟踪问题,基于滑模控制理论设计了一种分层滑模控制器,并证明了在分层滑模控制器控制下闭环系统的稳定性．数值仿真与实物平台分别验证了所提出控制策略的有效性．