高速铁路列车接续时刻调整优化方法

刘 旭，付慧伶，徐 能，张婷婷

（1.北京交通大学，交通运输学院，北京 100044；2.北京交通大学，智慧高铁系统前沿科学中心，北京 100044；3.中国国家铁路集团有限公司，调度中心，北京 100844）

0 引 言

高速铁路作为我国居民出行的重要交通方式，列车服务质量很大程度上影响着人们出行的便捷性。我国高速铁路网规模大、线路长、车站多，尽管列车运输计划以直达客流输送模式为主，开行较多距离长、停站多的旅客列车，但受制于列车起讫点设置、动车组运行里程、列车旅速要求（限制停站次数）等技术条件，根据近年列车时刻表数据统计，仍有超过70%的客流起点站与终点站（OD）之间没有直达列车服务，这些OD 之间的旅客不得不换乘出行。目前，我国在编制高速铁路列车开行方案和运行图时，仅关注主要方向上重点车站之间换乘客流的接续，从路网角度规划列车接续方案的全局性与合理性不足，使得部分列车之间接续关系的形成带有一定随机性，一些OD 存在接续时间长、接续频率低、同城异站接续等问题，降低旅客的换乘效率。因此，随着高速铁路网规模不断扩大、换乘客流量持续增加，列车接续方案亟须优化。

几十年来，国内外学者针对铁路列车接续方案优化问题展开了大量研究，表1列举了一些代表性研究。部分学者在周期列车运行模式下探索接续方案改进方法。周期模式中，列车运距短、开行密度大，在各周期（一般为1～2 h）内呈现相同的停站和运行时分特征[1]，列车之间自然形成很多规律化的接续关系，优化列车接续时必须满足周期约束，侧重接续时间和接续频率的精细化。代表研究如Karl 等[2]通过调整周期运行图建立列车换乘协调优化模型，提出了应用模糊逻辑的混合遗传算法；郭根材等[3-4]建立列车接续约束生成模型和基于备选列车接续的周期运行图编制模型，采用融合进化贪婪思想的启发式算法求解案例；徐涵等[5]构建考虑灵活接续的周期运行图加线模型，实现接续方案与运行图综合优化；李天琦等[6]改进传统CPF（Cycle Periodicity Formulation）模型构建运行图与接续方案协同优化模型，给出了运用贪婪策略的圈基搜索算法。实践中，德国、瑞士等国铁路经过多年市场优化不断调整列车时刻，形成了具有0.5 h、1 h等节拍规律的周期性列车接续方案[7]。

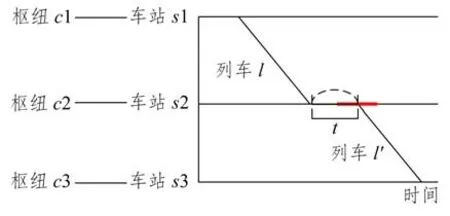
图1 列车同站接续方式示意图Fig.1 Train connection at the same station

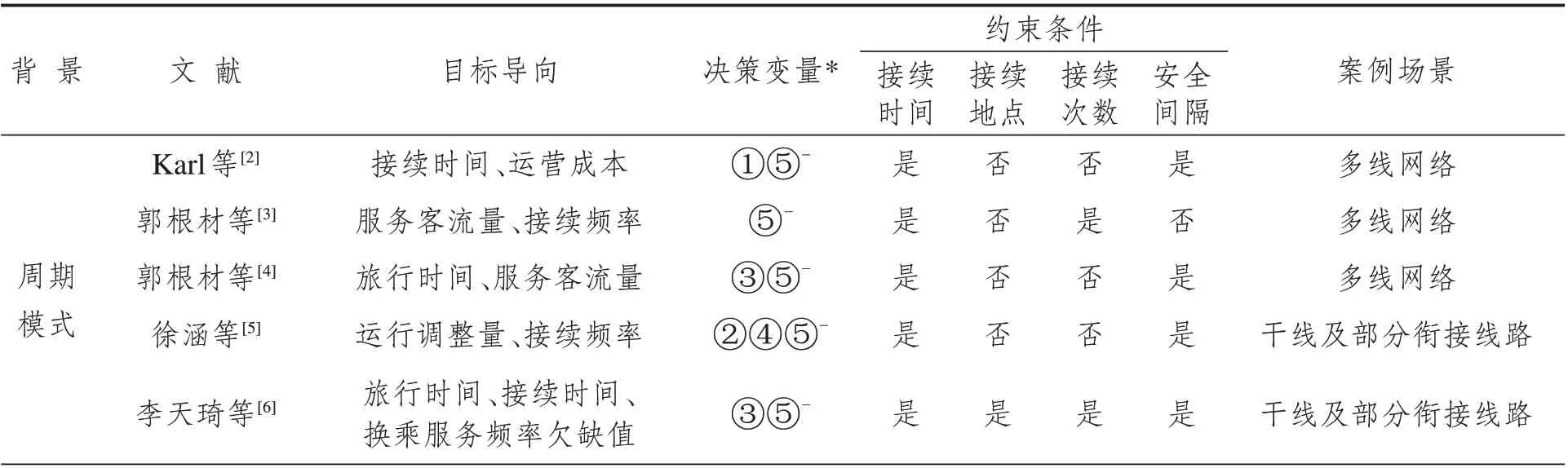
表1 铁路列车接续方案相关研究对比Tab.1 Comparison of train connection plan studies

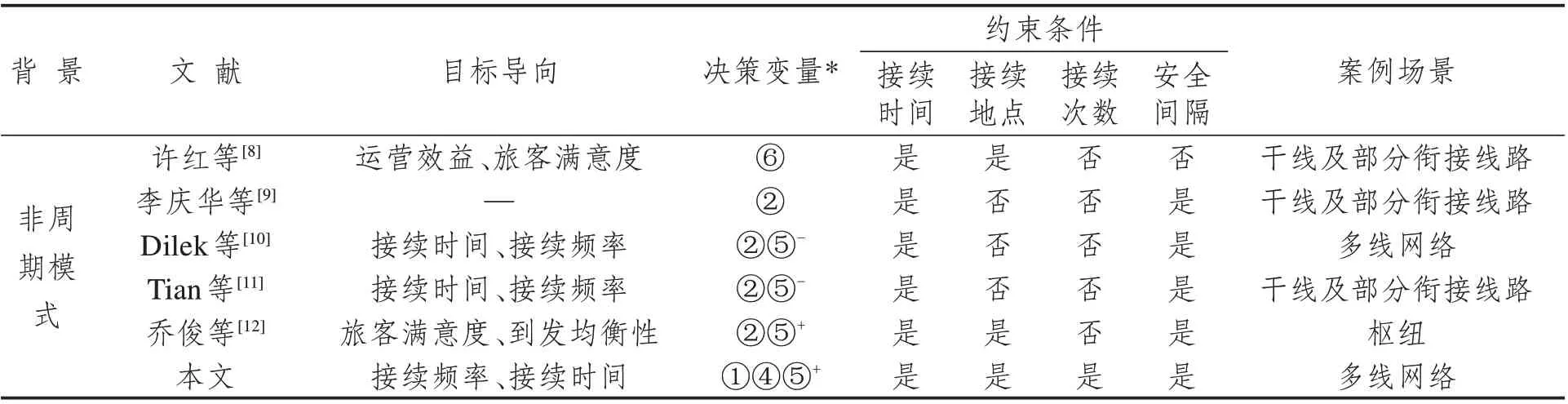
续表1

部分学者在非周期列车运行模式下研究接续方案优化问题。非周期模式中，为了适应客流在时间和空间上的不均衡分布，路网中大量不同运距和停站类型的列车以不同的频率和运行时分不规律开行，构造列车之间的接续关系不受周期约束而更加灵活复杂。如许红[8]兼顾铁路旅客和运输企业双方利益建立客运专线枢纽接续方案优化模型，提出采用分块编码的改进遗传算法；李庆华[9]运用同余理论构造多列车换乘衔接模型，模拟验算各方向列车的合理发车时间范围；Dilek 等[10]研究具有不均衡发车间隔的运行图同步协调问题，权衡换乘等待时间和列车旅行时间；Tian 等[11]构建列车时刻表综合协调优化模型，设计启发式算法顺序求解具有优先级的多目标数学规划问题；乔俊等[12]建立基于换乘协同的客运枢纽列车接续优化模型，设计改进遗传算法提高模型求解效率。

另有研究关注列车接续稳定性，如赵森[13]等指出列车到达晚点可能破坏站内列车接续关系；Mohideen[14]构建周期运行图稳定性仿真模型，分析列车接续次数对晚点传播的影响；Keyhani[15]基于列车晚点概率分布建立接续方案稳定性评价模型；党维婧[16]等通过优化换乘客流组织方式保证列车晚点情况下站内接续稳定性；Yuan 等[17]从缩短接续时间和稳定接续关系两方面优化列车接续。

本文基于我国高速铁路非周期列车运行模式建立列车接续方案优化模型。根据表1对比，周期与非周期模式下的接续方案相关研究除“周期约束”外，在模型结构上表现出部分共性特征，均对本文研究具有借鉴意义，但仍存在局限性：

（1）既有研究大多以最大化接续频率和最小化接续时间为目标，但没有根据不同OD 之间的客流量、直达列车开行频率等差异区别设计列车接续服务水平，不利于列车时空服务资源的合理配置。

（2）既有研究在决策列车时刻或列车时刻调整量时，大多固定列车到发顺序或预先指定列车接续地点且不考虑异站接续的可能性，限制了路网中多车站与多列车之间接续耦合的灵活性。

（3）既有研究为了提高列车接续频率，往往不限制单次列车运行全程与其他列车的接续次数，忽略了接续关系对运行图稳定性的影响，接续次数过多会加剧列车晚点情况下运行图的调整难度。

为解决上述问题，本文构建的列车接续方案优化模型以结合各OD 换乘需求差异最大化列车接续频率和最小化列车接续时间为目标，基于既有运行图调整列车在车站的到发时刻和顺序，改变路网中不同方向线路上运行的多趟列车之间在枢纽内一个或多个车站的接续关系，灵活决策接续列车、接续地点和接续时间，并增加确保运行图稳定性及可行性的列车接续次数、追踪间隔时间等约束，通过优化列车接续时间、接续频率和接续方式，实现接续方案质量的提升，为铁路部门调整列车运行图提供参考和依据。

1 列车接续时刻调整优化问题描述

在高速铁路网中，列车接续方案决策输送换乘客流的前序列车、中间的换乘车站、接续时间和可换乘的后序列车[1]。由于高速铁路旅客对出行便捷性有较高要求，多次换乘显著降低其乘车意愿，本文仅考虑各OD之间旅客一次换乘的情况。

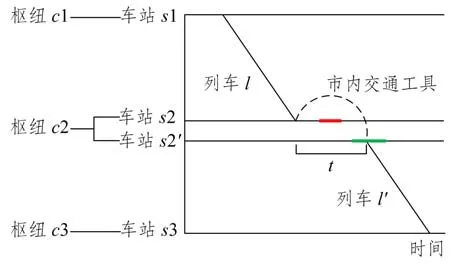
图2 列车异站接续方式示意图Fig.2 Train connection at different stations

一个铁路枢纽内往往开行路网中不同方向线路的列车，如图3 所示，这些列车在枢纽内灵活组合形成一对一（l6 为l5 的前序列车）、一对多（l5为l2 和l4 的前序列车）、多对一（l3 和l5 为l2 的前序列车）等多种同站或异站接续关系，以满足不同方向客流OD 之间的旅客换乘需求。从图3 可以看出，一趟列车可以在多个枢纽与多趟列车接续，若调整图3 中列车l2 在郑州枢纽的到发时刻，将影响该列车在其他枢纽（如石家庄枢纽）内与其他列车（如列车l1）的接续时间和接续频率。路网条件下多枢纽、多车站以及多列车之间具有复杂耦合接续关系，需要在接续方案质量提升目标和接续时间、地点、次数、列车安全运行等约束下进行优化决策。

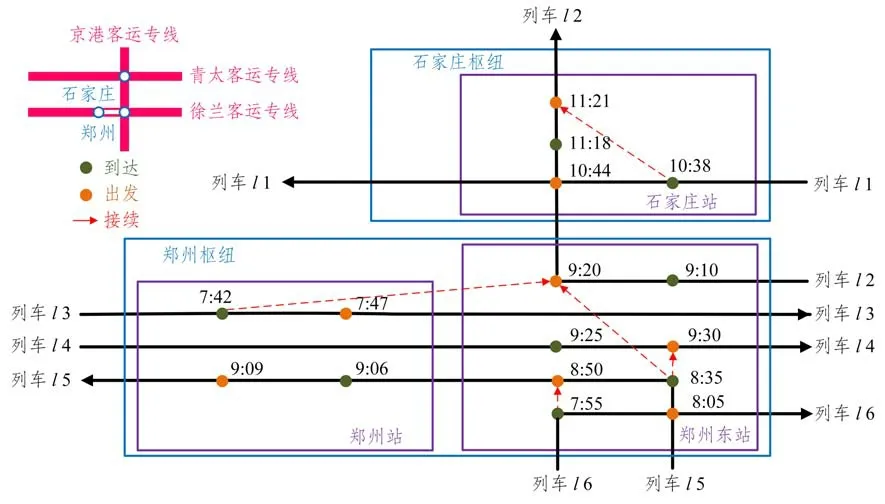
图3 铁路枢纽内各类列车接续关系示意图Fig.3 Various train connections in railway hubs

为了优化高速铁路列车接续方案，可基于既有列车运行图，通过调整列车在车站的到发时刻和顺序，改变路网中不同方向线路上运行的多趟列车之间在各个枢纽内一个或多个车站的同站或异站接续关系，针对目标客流OD实现以下优化效果：

（1）维持原本存在的有效列车接续关系，并尽量缩短其接续时间，如图4所示。

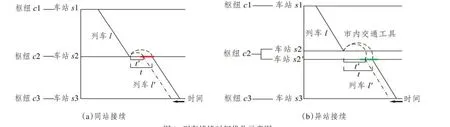
图4 列车接续时间优化示意图Fig.4 Optimization diagram of train connection time

（2）使部分原本不接续的列车之间形成有效接续关系，增加列车接续频率，如图5所示。

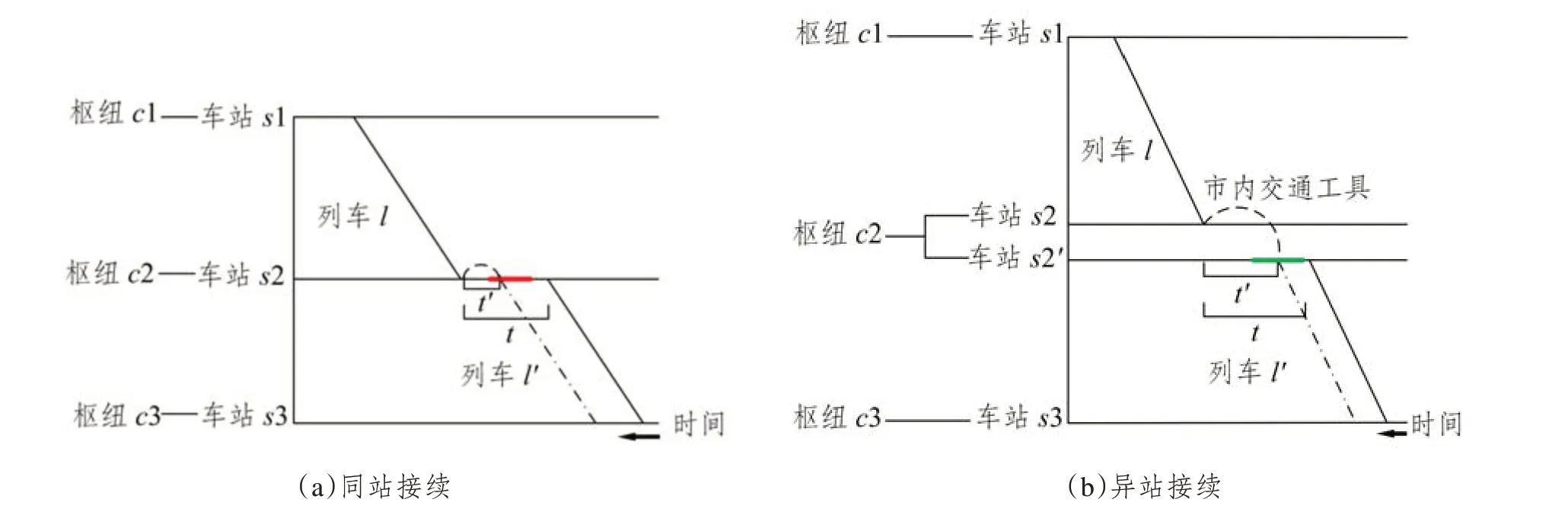
图5 列车接续频率优化示意图Fig.5 Optimization diagram of train connection frequency

（3）使部分原本仅满足异站接续条件的列车之间转变为有效的同站接续关系，优化列车接续方式，如图6所示。

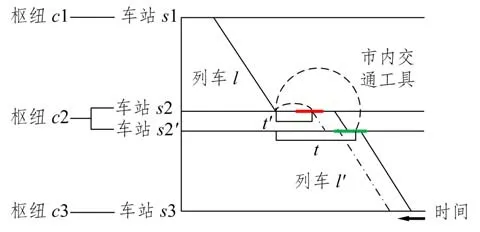
图6 列车接续方式优化示意图Fig.6 Optimization diagram of train connection location

2 列车接续时刻调整优化模型

本文针对我国高速铁路非周期列车运行模式，建立列车接续时刻调整优化模型，考虑图3 中的灵活列车接续关系，调整既有运行图中列车在车站的到发时刻和顺序，优化列车接续时间、接续频率和接续方式，提高列车接续方案质量。

2.1 模型的目标函数

从铁路旅客和运输企业双方利益出发，以结合各OD 换乘需求差异最大化列车接续频率和最小化列车接续时间为目标，将两个目标函数加权合并，转化为目标函数（1）：

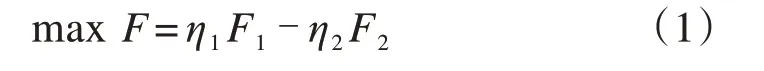
式中：η1与η2分别表示目标函数F1与F2的权重系数。F1与F2的具体含义如下：

（1）列车接续频率最大化目标函数F1

一个OD 之间的列车接续频率越高，意味着铁路运输企业分配给该OD 的列车时空服务资源越多。结合历史客流数据及列车时刻表，根据各OD之间单日内的中转客流量、直达客流量和直达列车开行频率等指标，为不同OD 赋予不同权重。权重值越大的客流OD，在列车接续频率优化过程中具有越高的优先权。考虑各OD 换乘需求差异区别提升列车接续服务水平，有利于优化铁路列车时空服务资源在客流OD 之间的配置。最大化列车接续频率的函数表达如下所示：

为重点提高中转及直达客流较多、而直达列车开行频率较低的OD 之间的列车接续频率，第k对客流OD的权重δk根据下式计算：

（2）列车接续时间最小化目标函数F2

列车接续时间决定旅客在换乘站的等待时间，在站等待时间过长会增加旅客全程旅行时间，降低旅客出行满意度，不利于吸引客流。最小化列车接续时间的函数表达如下所示：

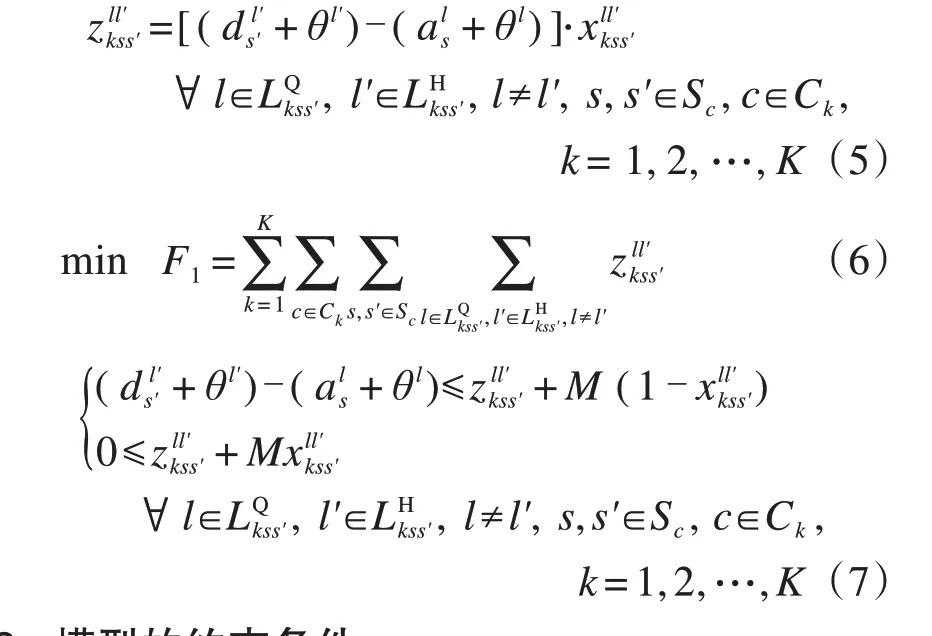
2.2 模型的约束条件

（1）列车接续时间约束为保证旅客换乘的效率与安全，在同一枢纽，前序列车到达时刻与后序列车出发时刻应符合一定时间间隔要求，如下所示：

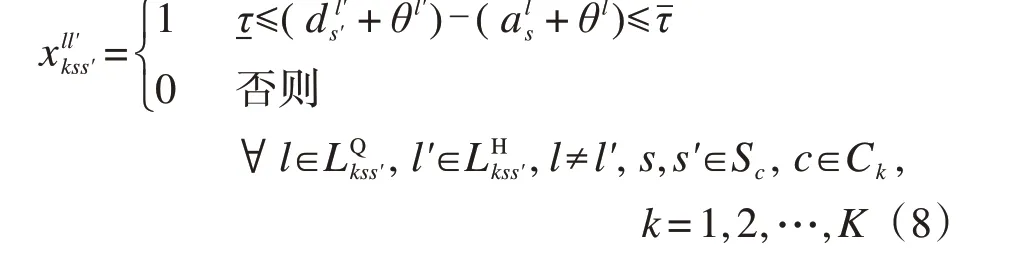
式中：-τ和τˉ分别表示合理列车接续时间的下限和上限。

根据调研统计，长距离OD 旅客对同站换乘时间的选择以30～45 min为中心呈正态分布，对异站换乘时间的选择以70～100 min为中心呈正态分布[19]。在旅客可接受的换乘时间范围内，按照目前的车站客流组织方式，可设定同站换乘合理接续时间为40～60 min，异站换乘合理接续时间为90～120 min。

（2）列车接续地点约束

为了灵活决策列车接续地点，将接续列车相同、接续地点不同的若干列车接续归为一组，每组列车接续满足接续地点唯一性约束（13）。在目标函数F2的作用下，针对一组列车接续，若列车在多个枢纽满足合理接续时间要求，模型将选择接续时间最短的列车接续；若列车在同一枢纽同时满足同站换乘与异站换乘合理接续时间要求，模型将决策出接续时间较短的同站接续，以便旅客换乘：

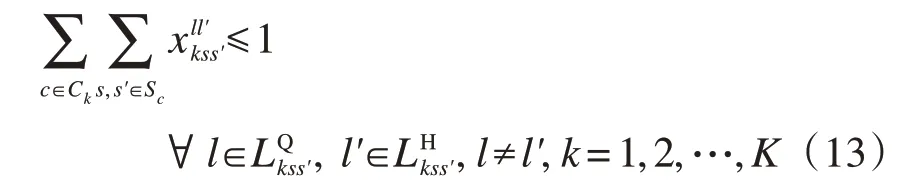
受车站换乘设备数量和换乘客流组织能力的影响，单日内车站接续能力有限，考虑到异站换乘客流相当于前序换乘站的出站客流和后序换乘站的进站客流，可用约束（14）限制单日内车站的同站接续次数，避免列车接续过多集中于某一车站：

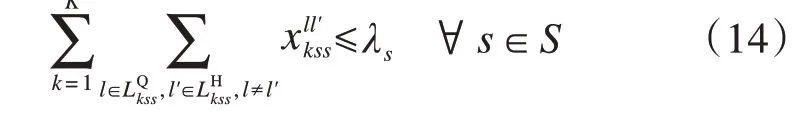
式中：λs为单日内车站s的最大列车接续次数（次/d），可结合我国高速铁路车站的实际情况确定。

（3）单次列车运行全程与其他列车接续次数约束

我国高速铁路列车运行距离普遍长，干线列车密度高，本线与跨线列车耦合紧密，如果列车在运行全程与其他列车接续次数过多，当列车发生晚点时，为了维持接续关系，会加剧晚点传播，增加列车运行调整难度[20]。因此，利用约束（15）限制列车之间的接续次数：

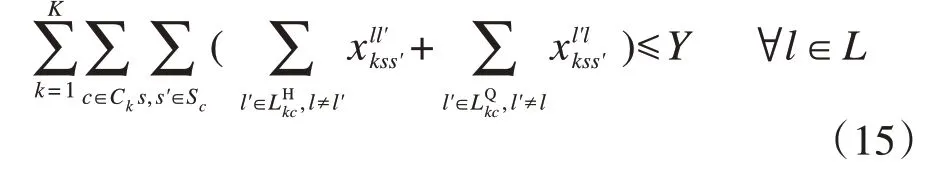
式中：Y为单次列车运行全程与其他列车的最大接续次数，可参照现状接续方案确定。

（4）列车时刻调整量约束

为尽可能少地变动列车在车站的到发时刻，减少对既有运行图结构的影响，用约束（16）限制列车时刻调整量：

（5）列车运行时间范围约束

我国高速铁路列车运行时间多为6:00～24:00，约束（17）保证调整后各列车的始发和终到时刻均在列车日间运行时间范围内：

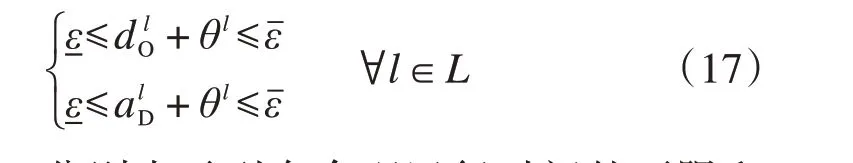
式中：-ε和εˉ分别表示列车合理运行时间的下限和上限，取值为360 min 和1 440 min与分别表示列车l的始发时刻和终到时刻。

（6）追踪列车间隔时间约束

调整列车时刻后为了保证运行图可行性，应满足追踪列车安全间隔要求。考虑到我国高速铁路列车一般存在速差，将列车追踪间隔时间约束分解为以下三个与列车区间运行时间无关的约束：约束（18）确保列车从区间起点车站出发（或通过）时满足间隔时间要求；约束（19）确保列车到达（或通过）区间终点车站时满足间隔时间要求；约束（22）禁止多速差列车发生区间越行。

约束（18）和（19）具有非线性特征，通过约束（23）和（24）将其线性化：

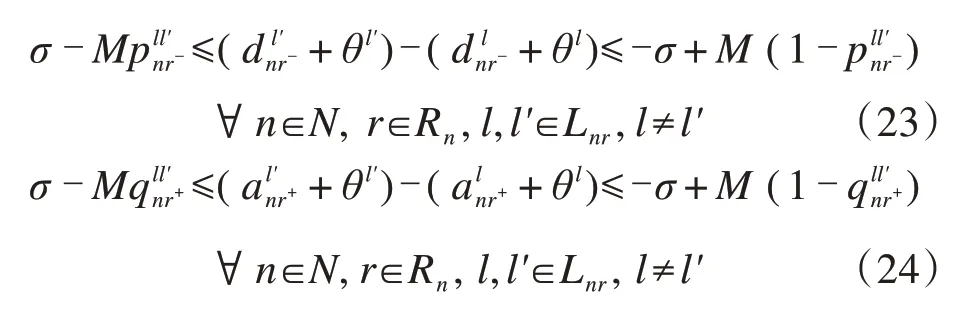
综上，具有非线性特征的目标和约束经线性化处理后，高速铁路列车接续时刻调整优化模型转化为一个线性整数规划模型。

3 实例研究

3.1 实例背景

选取“四纵四横”高速铁路网进行实例研究，如图7所示。基于某年度列车时刻表和对应的OD客流数据分析可知，对于里程低于500 km 的短途客流，高速铁路以提供直达列车服务为主。同时，据问卷调查统计，出行距离在500 km 到900 km 的中短途旅客换乘意愿较低；而很多里程高于900 km的客流OD之间的旅客由于直达列车频率不足等原因需要换乘出行。因此，从“四纵四横”高速铁路网中筛选出900 km 以上的1 915 对长距离客流OD，作为列车接续方案的重点优化对象。利用公式（3）计算各客流OD权重，表2展示了部分计算结果。

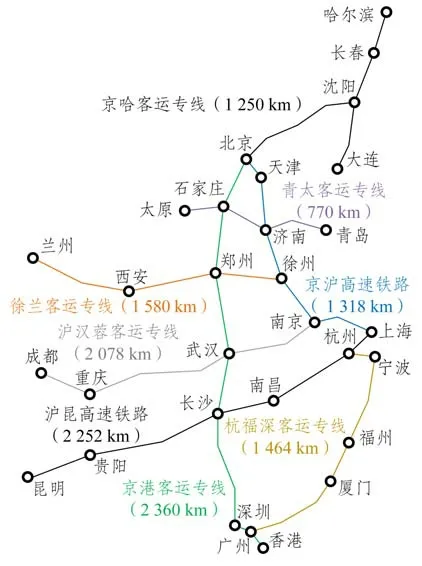
图7“四纵四横”高速铁路网Fig.7 China’s“Four Vertical and Four Horizontal”HSR network

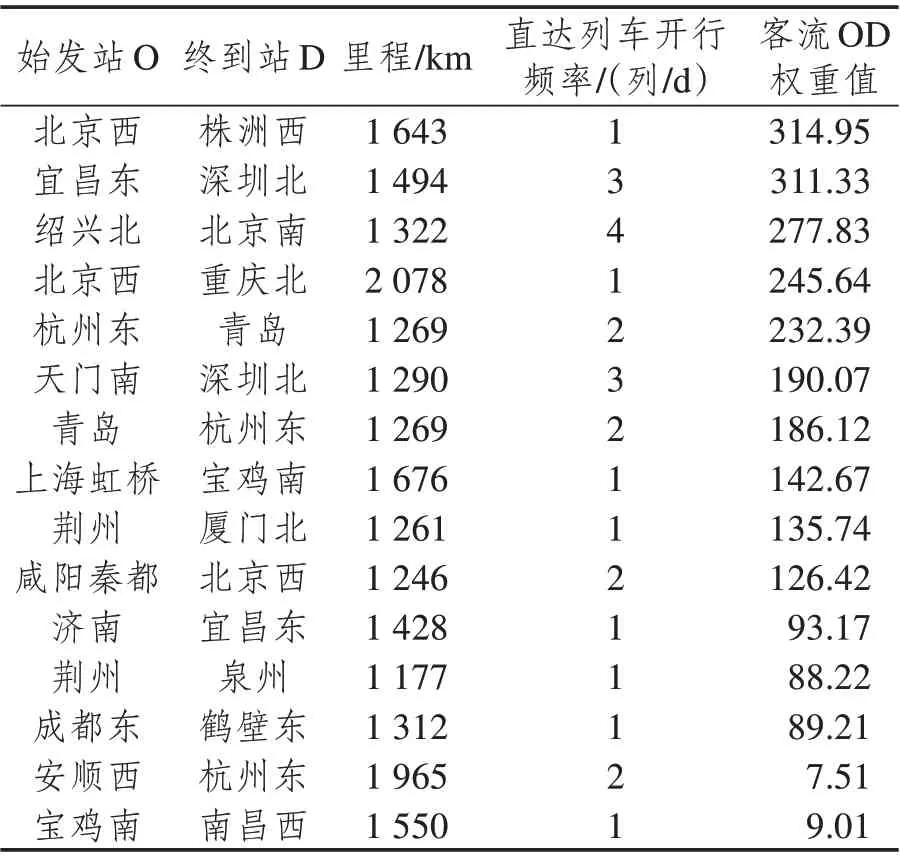
表2 部分客流OD优化权重的计算结果Tab.2 Optimization weight calculation results of some passenger OD pairs

由于我国铁路没有明确给出现状列车接续方案，本文从时刻表数据中调取可能为上述1 915 对客流OD 提供换乘服务的2 767 列列车，生成有效的23 809 个同站接续（接续时间取40～60 min）和8 824 个异站接续（接续时间取90～120 min）的现状列车接续方案；同时，生成待优化的35 655 个同站接续（接续时间取10～90 min）和11 572 个异站接续（接续时间取60～150 min）的列车接续备选集合。列车接续备选集合包含现状列车接续方案，有的客流OD之间只存在单方向列车接续。

3.2 优化结果

在实例测试中，因目标函数F1与F2量纲相差不大，为平衡目标函数F1与F2，两者的权重系数均取值为0.5，设置列车时刻调整范围为-5～5 min、-10～10 min、-15～15 min 三 种 场 景，使 用Visual Studio 2019结合C#语言编程处理客流数据和列车接续信息，并调用CPLEX 求解列车接续方案优化模型，运算环境为Win10-64 位操作系统、16G 内存、11 代 酷 睿i5-1135G7 处 理 器。当Gap 值 设 为5% 时，三种场景下模型的求解时间分别为2 291.14 s、17 345.33 s和45 700.82 s。

三种列车时刻调整范围场景下优化后的部分列车接续方案如表3所示，可以看出优化后列车之间的接续时间趋于合理，接续频率略有提高，接续方式也有所改善。当θ范围不同时，同一客流OD对应的列车接续时间、接续频率和接续方式没有明显的变化规律。

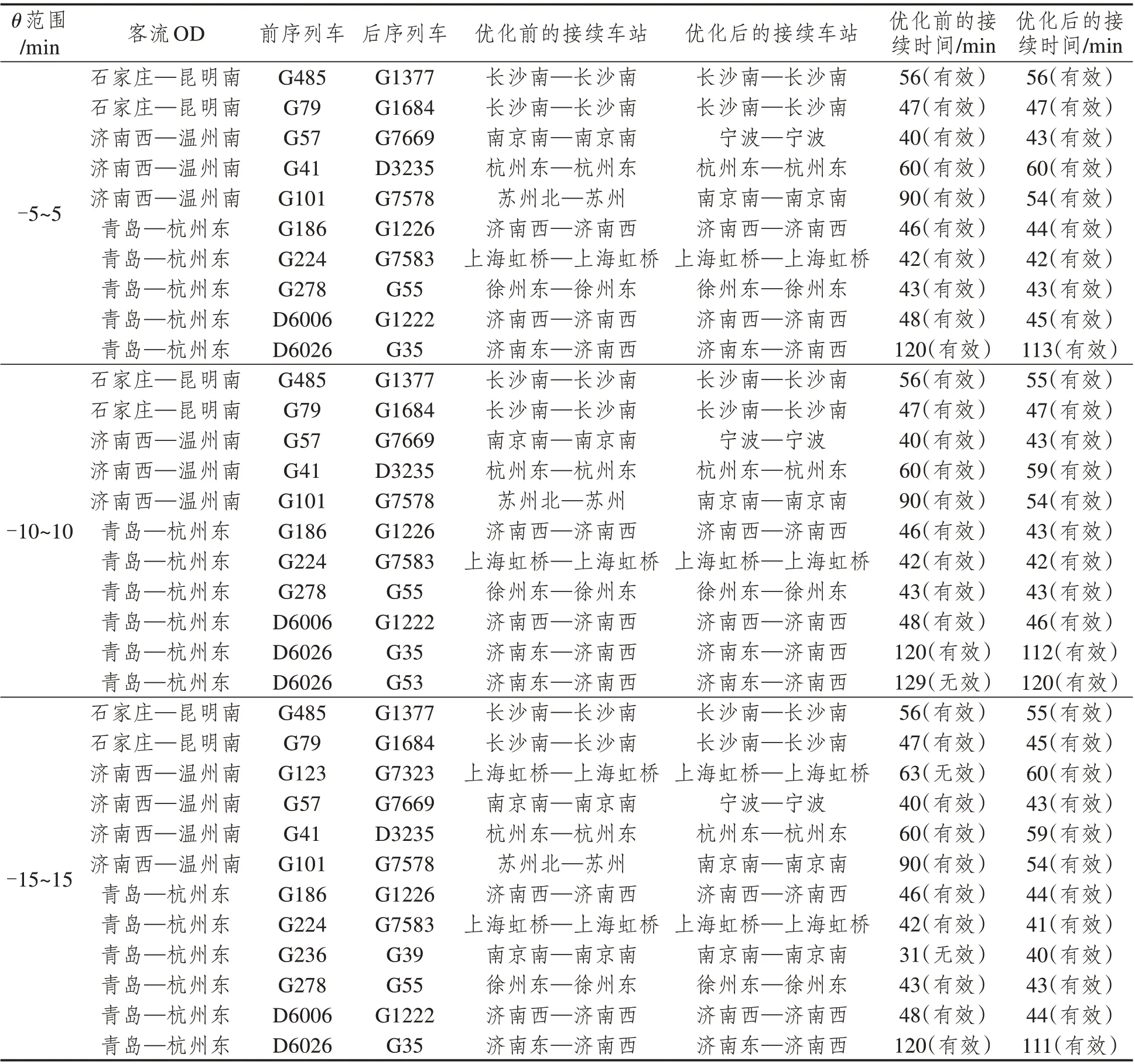
表3 三种优化场景下的列车接续方案优化结果（部分）Tab.3 Optimization results of train connection plan under three optimization scenarios（some）

三种列车时刻调整范围场景下不同权重客流OD 对应的列车接续方案优化结果如图8 所示，接续服务质量提升效果如表4 所示。可以看出客流OD 权重值越大，列车接续时间、接续频率和接续方式的优化幅度越大；优化后的接续方案使列车时空服务资源在不同OD之间得到更合理的配置。

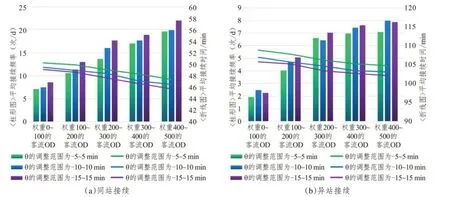
图8 三种优化场景下不同客流OD的列车接续方案优化结果Fig.8 Optimization results of train connection plans of different passenger OD pairs under three optimization scenarios

表4 三种优化场景下不同客流OD的接续质量提升效果（部分）Tab.4 Improvement effect of connection quality of different passenger OD pairs under three optimization scenarios（some）

与现状列车接续方案相比，三种列车时刻调整范围场景下优化得到的接续方案服务指标统计结果如表5所示，旅客换乘服务水平的提升效果如图9所示。对比分析可知：列车时刻调整范围越大意味着调整越灵活，增加的列车接续频率越高，缩短的列车接续时间越长，由异站换乘优化为同站换乘的列车接续数量越多，客流OD 的换乘服务质量提升幅度越大，列车接续方案总体优化效果越好。但是运行图列车时刻调整会带动站内列车走行进路、动车组交路、乘务交路等一系列计划的调整，服务质量越好的列车接续方案对既有运行图结构的影响越大，实施难度也越高。

表5 三种优化场景下列车接续方案服务指标对比Tab.5 Comparison of service indexes of train connection plans under three optimization scenarios

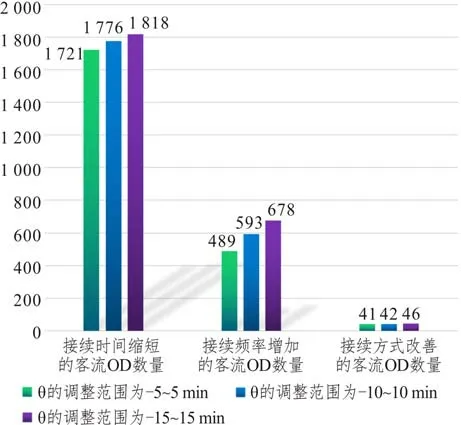
图9 三种优化场景下旅客换乘服务水平提升效果Fig.9 Improvement effect of passenger transfer service level under three optimization scenarios

为分析目标函数中F1与F2的权重系数取值对列车接续方案优化结果的影响，选取列车时刻调整范围为-5～5 min 场景，模型其他参数值保持不 变，设置η1η2=0.2 0.8，η1η2=0.5 0.5，η1η2=0.8 0.2三组目标函数权重比值。三组比值下优化得到的列车接续方案服务指标统计结果如表6 所示，旅客换乘服务水平的提升效果如图10 所示。对比分析可知：三组比值下列车接续时间、接续频率和接续方式都实现了优化；η1η2比值越大（即模型越侧重优化列车接续频率目标），列车接续频率的增加幅度越大，列车接续时间的缩短幅度越小，相应地接续频率增加的客流OD 数量越多，接续时间缩短的客流OD数量越少，可见η1与η2能够权衡两个优化目标之间的关系，验证了模型的合理性。

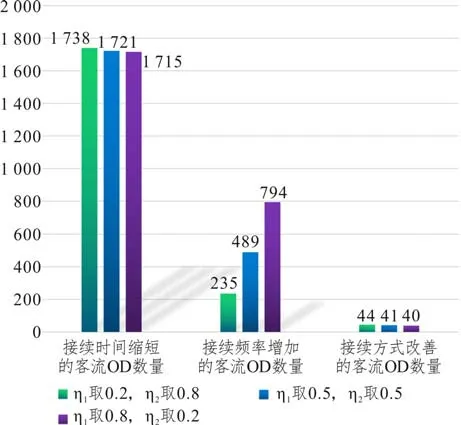
图10 三种目标权重比值场景下旅客换乘服务水平提升效果Fig.10 Improvement effect of passenger transfer service level under three scenarios with different objective weight ratios

表6 三种目标权重比值场景下列车接续方案服务指标对比Tab.6 Comparison of service indexes of train connection plans under three scenarios with different objective weight ratios

综合上述分析可以看出：针对“四纵四横”高速铁路网中的长距离客流OD，利用所提出模型优化得到的列车接续方案与现状接续方案相比，达到了缩短接续时间、提高接续频率和改善接续方式的优化效果，并使列车时空服务资源在不同客流OD 之间得到更加合理的配置，可以作为铁路部门改善列车接续方案质量，提升旅客换乘服务水平的运行图调整依据。

4 结束语

本文针对我国非周期列车运行模式下的高速铁路网列车接续方案优化问题进行研究。以结合各OD 换乘需求差异最大化列车接续频率和最小化列车接续时间为目标，建立列车接续时刻调整优化模型，通过适当调整既有运行图中列车在车站的到发时刻和顺序，优化列车接续时间、接续频率和接续方式。案例以“四纵四横”高速铁路网中运距超过900 km 的1 915 对客流OD 为研究对象，涉及2 767 列列车和47 227 个备选列车接续。当目标函数的权重系数均取值为0.5、允许列车时刻向前或向后最多移动5 min、10 min 和15 min 时，模型求解结果表明：优化后的列车接续方案与现状方案相比，列车接续频率至少提高941 次，总列车接续时间至少缩短16 945 min，超过45 个列车接续由异站接续优化为同站接续，至少1 736 对客流OD 的换乘服务质量得到提升，权重越大的客流OD 接续质量提升幅度越显著，并且列车时刻调整范围越大，接续方案优化效果越好。此外，在案例中分析了不同目标函数权重系数比值对列车接续方案优化结果的影响。案例研究验证了优化模型的合理性和有效性。

本文研究仍有待完善之处：一是在目前选取的高速铁路网实例规模下，借助现有求解器求解模型耗时较长，如果把路网中全部列车和更多客流OD 纳入优化范围，则需要设计有效的求解算法；二是模型中假设同一列车在运行径路上各站的到发时刻调整量相同，一些原本由于越行导致的较长停站时间，平移列车运行线后在越行消失的情况下仍然保持不变，可能造成路网局部通过能力的浪费，需进一步研究列车在各站到发时刻灵活调整的情况，但这将增加模型复杂性；三是模型未包含车站间隔时间约束，即未考虑复杂的车站到发线运用和咽喉区进路排列，因此优化后的接续方案仅支持宏观运行图兑现，路网条件下接续方案与微观运行图的协同优化是一个更具现实意义但更具挑战的问题。