机场群航班时刻表优化方案研究

吴慎之，王子明，杭 旭，王艳军

（1.南京航空航天大学，民航学院，南京 211106；2.中国民航，中南地区空中交通管理局，空域办，广州 510405）

0 引 言

航空运输业是我国交通运输体系的重要组成，在国民经济发展中起着重要的作用。虽然近年来航空运输需求的增长速度受到疫情影响有所减缓，但是从长远来看需求将会持续增长。在一些主要机场，航空公司安排航班的需求一直超过机场的服务能力，造成交通拥挤和航班延误。为了解决这一问题，一方面可以通过扩大机场基础建设，或研发新的空中交通管理技术来增加机场容量，以满足运输需求；另一方面，可通过有效的需求和容量管理，提高现有机场容量利用效率和效益。机场航班时刻优化配置是需求管理的有效手段之一，也是航空运输领域的一个重要研究方向。然而，现有的研究主要面向单一机场的时刻分配，鲜少有针对机场群或多机场系统内多个机场协同优化的研究。加快世界级机场群建设是我国民航运输业“十四五”期间的一项重要工作，优化合理配置机场群的时刻具有非常重要的理论价值和现实意义。

目前，世界上大多数国家的繁忙机场都依据国际航空运输协会(International Air Transport Association,IATA)发布的全球航班时刻指南（Worldwide Airport Slot Guidelines,WASG）每年开展两次时刻分配，即夏航季和冬航季[1]。每个机场都会提前公布时刻容量（或称为时刻协调参数），给出1小时或15分钟内可以通过的航班数量。航空公司向时刻协调部门或时刻协调人提交航班时刻申请。时刻协调人基于公布的时刻管理法对航空公司的申请进行协调，协调结果包括批准所申请的时刻、调整时刻和拒绝申请的时刻。航空公司只能在被批准的时刻内使用机场的基础设施，安排进场或离场航班。航班时刻优化问题旨在满足机场时刻容量约束、时刻配置规则等前提下，对航空公司的时刻申请进行优化配置，以最大限度地满足需求，提高容量利用效率[2]。Koesters 等人[3]建立了一种确定性方法，用于模拟时刻分配过程并计算了各种公布容量和需求的计划延误。2011 年，Zografos等人[4]基于IATA 规则、运营限制和时刻协调程序，在战略层面上开发出一个单机场时刻优化模型，来改善欧盟机场的容量分配，该模型的目标是最小化航空公司时刻请求和优化后时刻之间的差异，以此更好地适应航空公司的时刻偏好，且通过与希腊三地区机场航班时刻分配结果对比，发现使用该模型能够将航空公司时刻偏好的保持度提高到14%到95%。Jacquillat 等人[5]为解决机场需求和容量之间的不平衡，提出一种综合方法将航班时刻优化战略和战术相结合，即在战略层面优化机场航班时刻表，战术层面优化机场容量和延误降低约束的机场容量，并开发了一种原始迭代求解算法，集成了机场随机排队模型、容量利用率的动态规划模型和计划干预的整数规划模型，并以纽约肯尼迪机场为例进行验证，计算结果表明可以通过对75%～90%的航班进行有限更改（每架航班调整不超过30 min）就能大幅降低延误。2016 年，Pyrgiotis 等[6]将一种需求平滑的优化模型(DS)和新的网络排队论模型相结合，发现在纽瓦克机场引入模型得到的时刻表，能减少本地延误20%～50%。2017 年，Zografos 等人[2]对航班时刻优化问题研究以及公布容量建模进行了综述，指出未来航班刻时分配研究需要用公平性、资源利用和环境考虑来丰富模型目标，未来的研究应致力于航空公司对航班分配结果的可接受性，并建立稳定可行的模型，刻画机场运营的复杂性、动态性以及天气的不确定性。2018年，Ribeiro等人[7]考虑WASG 时刻配置规则，提出了一个基于优先级的多目标航班时刻分配模型（PSAM），并应用在葡萄牙的两个机场，研究结果表明，PSAM 可以改善繁忙机场的航班时刻分配结果，且PSAM 还可以量化航班时刻分配决策对WASG 指南中规定的各种优先级和要求的敏感性。2019年，Ribeiro等人[8]基于PSAM 开发了一种新的解决方案来求解模型，并提出一个实验设计来评估时隙分配规则和程序的变化，该模型被应用在葡萄牙不同规模的机场，结果表明对WASG 进行一些有限的改变能在短期内为时隙分配带来可观的收益。Zografos等人[9]建立同时考虑公平性和效率的双目标优化模型，并采用ε-约束方法和行生成算法来求解模型，研究了考虑历史时隙使用权以及不考虑历史时隙使用权的两种优化机制下的效率公平权衡。2019 年，汪梦蝶等[10]针对时刻表的功效性和可接受性之间关系，基于可接受调整量水平，建立航班时刻优化模型，采用ε-约束法和改进粒子群算法求解，并应用于南京禄口机场，发现航空公司对可接受调整量水平的阈值越严格，由航班调整总量代表的成本就越高。2020 年，Androutsopoulos 等人[11]将战略机场时刻分配转化为具有部分可再生资源和非规则目标行数的双目标资源约束优化问题，引入平方位移标准减轻航班时刻请求的过度偏移。并提出一种新的混合启发式算法将FP 算法和LNS 相结合用于逼近帕累托最优解，应用在希腊地区，结果表明算法具有合理的准确度。2021 年，Jorge 等人[12]提出了一种基于PSAM优化的决策支持工具，用于初始时刻分配时协助时刻协调员，考虑到全球时刻指南的所有标准，通过优化模型处理航班分配问题。2020 年，Fairbrother 等人[13]考虑到在协调机场分配航班时刻的阻塞问题，提出了一种新的航班时刻分配模型，该模型通过限制分配时间的范围来考虑时刻表的规律性，并采用两种启发式算法来构建热启动解决方案，研究结果表明季节的划分是一种更有效的方法，可以改善阻塞的影响。部分学者针对机场网络的时刻优化配置进行了研究，如Pellegrini 等人[14]考虑机场容量、飞行时间和航班离场时间及到达时间的连接，提出了一个整数线性规划模型（SOSTA）为所有机场分配时刻并以欧洲机场网络为例进行了实验，优化效果显著。2018，Benlic 等人[15]提出了一种启发式算法用于求解机场网络时刻优化模型，该算法包括构造性启发式方法（生成可行的初始解并消除在始发地和目的地找不到一致的时刻分配的航段）和迭代启发式方法（根据时刻表延误（分配的时间段和航空公司请求之间的时间差）提高初始解决方案质量），并且通过实验发现与每个机场独立分配航班时刻相比，考虑航路约束不会导致时刻表显著退化。然而，该算法只能优化欧洲机场网络一天的航班时刻表，不适用于整个航季的时刻表优化。

虽然在单机场时刻优化研究工作取得了丰富的成果，但是关于机场群或多机场系统时刻优化的相关工作鲜有开展。然而，有关机场群的战术运行相关研究已得到长足的发展[16-17]。美国联合发展与规划办公室[18]给出了多机场群的明确定义，即由位于大都市地区服务多个城市的多个机场组成，且其部分进离场航班会使用共同的空域资源。不同于单机场航班时刻优化，多机场航班时刻优化时需要考虑机场之间的相互影响和空域的运行容量限制[19]。2011 年，Clarke 等人[20]研究了美国四个主要机场群运行特点，确定了12个主要问题，其中影响最大的几个问题分别是共用的离场航路点、区域内共用空域管理和临近机场配置产生冲突运行。2012年，赵闯[21]分析了机场与航空OD 需求的关系以及机场相互之间的关系，提出航空OD需求在机场群上分配方法。2013 年，刘佳等人[22]针对枢纽机场延误，考虑机场群航班共同调度。2018 年，王倩和翟文鹏[23]针对机场群航班延误的空域资源、机场运能和航班调配要素建立机场群航班时刻优化模型，应用于珠三角多机场系统，实验结果表明，最终广州机场和珠海机场离场延误峰值分别下降20%和30%，深圳机场进港峰值降低20%。2021 年，朱金福等人[24]构建以机场群内准点率、航空公司市场占有率、旅客损失时间和机场功能定位四个指标最大化为目标的机场群航班时刻优化模型，采用粒子群优化算法求解，以长三角机场群为实例求解优化，结果表明航班在各时刻分布较为均衡。

综上，航班时刻优化需要对航空公司的时刻进行调整，改变或拒绝航空公司所申请的时刻，因此产生时刻偏移成本，同时，航班时刻表在实际运行中可能会出现航班延误，产生航班延误成本。过多的接受航空公司需求会减少时刻偏移成本，但有可能在运行上引起过多的航班延误，从而增大延误成本；反之，过多的拒绝或改变航空公司时刻需求，可能会在运行上降低航班延误。目前一个尚未解决的问题是如何平衡时刻偏移成本和航班延误成本。特别是在机场群中，由于共享空域资源引起的多个机场之间的交互，导致时刻偏移和航班延误之间的关系更加复杂，相关研究工作尚待开展。因此，本文面向机场群航班时刻优化配置问题，建立机场群航班时刻优化模型，通过AirTop 仿真计算优化前后的航班延误，研究单机场时刻优化、机场组合时刻优化和机场群整体时刻优化三种不同策略下的航班时刻偏移和航班延误（如图1 所示），为机场群航班时刻分配提供理论支持。

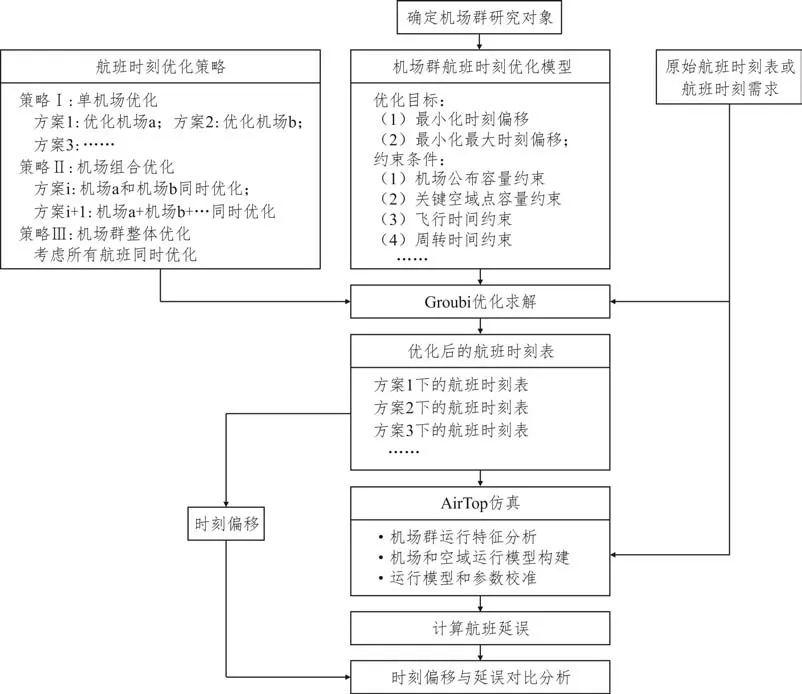
图1 机场群航班时刻优化策略研究框架Fig.1 Research framework for optimization schemes for schedules intervention in a multi-airport system

1 机场群航班时刻优化问题描述及模型假设

机场群航班时刻优化是指给定机场时刻容量、关键空域点容量和运行规则的前提下，优化调整航班时刻，最小化航空公司申请的偏移。与单机场时刻优化相比，机场群时刻优化需要考虑受限的空域资源和航班在机场与受限空域资源之间的飞行时间。在此，做出以下假设：

（1）航班的周转时间需不大于最大周转时间且不小于最小周转时间。周转时间是指前序航班到达后、后序航班离场之前的时间间隔，在周转时间内需要完成上下旅客、飞机加油等操作。

（2）仅考虑目标机场群内的机场航班，不考虑其在机场群外机场的航班起降时间及周转时间。

（3）航班在机场和机场群关键空域点之间的飞行时间为固定值。本文未考虑航班在机场与空域点实际飞行中可能考虑的机动（即飞行时间的不确定性），选取历史飞行时间的中位数作为机场和航路点之间的飞行时间。

（4）本文以航空公司现行时刻表作为时刻申请，不考虑航空公司之间的公平性，并且各航空公司能接受的最大调整量相同。

1.1 集合符号

（1）A={1,2,…,K+ 1}：机场集合，Κ为机场群内的机场个数，而Κ+1为一个虚拟的机场，包括时刻表中除机场群外的所有机场；

（2）P={1,2,…,N}：考虑分配时刻的时段集合，N为时段集合个数；

（3）F={1,2,…,V}：机场群内所有航班的集合；

（4）Fk⊂F：从机场k出发的离场航班和到达机场k的进场航班集合，Fk为F的子集；

（5）FC={(i,j)|i,j∈F}：联程航班集合，航班i,j使用相同的飞机，并且离场航班j为进场航班i的后序航班；

（6）DF={1,2,…,Q}：离场航路点的集合，其中Q为离场航路点的个数；

（7）AF={1,2,…,G}：进场航路点的集合，其中G为进场航路点的个数；

（8）MF={1,2,…,Z}：既可用于进场又可用于离场的航路点集合，其中Z为航路点个数；

1.2 参数符号

1.2.1 计划时间

1.3 决策变量

本文参考文献[5]，定义以下决策变量：

研究证明这种定义决策变量的方法能大大提升求解效率。例如，航班i在其计划机场k决策变量为{1,1,1,1,0,0,0,…}，则表示航班被分配到了第5个时刻从机场k起飞。航班i在其他机场的决策变量为{0,0,0,0,0,0,0,…}。

根据模型优化目标，令ui表示航班i的时刻偏移，即：

因此ui∈I,∀i∈F。

1.4 约束条件

1.4.1 由航班自身定义确定的约束

所有航班初始均未分配时刻的约束：

1.4.2 机场容量约束

各机场都存在进离场容量限制，即单位时间（15 min 或1 h）内安排的航班数量不能超过时刻容量。

机场离场航班容量约束和机场进场航班容量约束如下：

周转时间不小于β，β为联程航班对的最小过站时间，参考《民航航班正常统计办法》知γ=36，β=6：

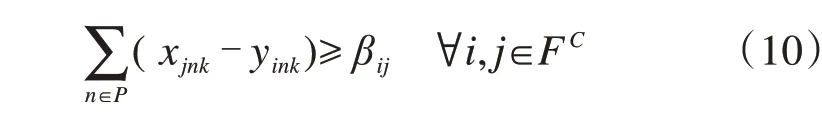
1.4.4 进离航路点容量约束

保证优化后的航班满足进离航路点的容量约束如下：

1.5 目标函数

模型的目标包括两个部分：一是最小化所有航班申请时刻的偏移；二是最小化最大的单架航班的偏移，故目标函数为：

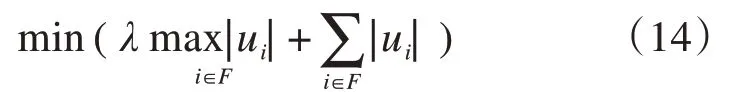
式中：λ为最大调整量的权重，参考文献[25]知λ=1。

1.6 模型求解

本文采用gurobi求解器对模型进行求解，并使用Python 作为建模语言实现。模型是在Window10 64位操作系统上运行，电脑配置为2.6 GHz、16 GB内存和i7处理器。

2 机场群时刻优化方案对比实例研究

2.1 实验设定

（1）粤港澳大湾区机场群。粤港澳大湾区机场群覆盖粤港澳三地九个城市，是我国三大世界级城市群之一，湾区主要机场包括香港、澳门、广州、深圳、珠海。作为全国最具经济活力、开放程度最高的地区，民航在其综合交通运输体系中的比重远高于全国平均31%的水平。2018 年，粤港澳大湾区五大机场的总体旅客吞吐量超过2 亿人次、货邮吞吐量近900 万t。由于空域资源非常紧张，航空延误、航路航班时刻资源不足问题日渐突出。机场的相对位置和进离场航线如图2所示，不同颜色的线表示不同机场的进离场航线，灰色的线为广州和珠海进近管制区的边界。

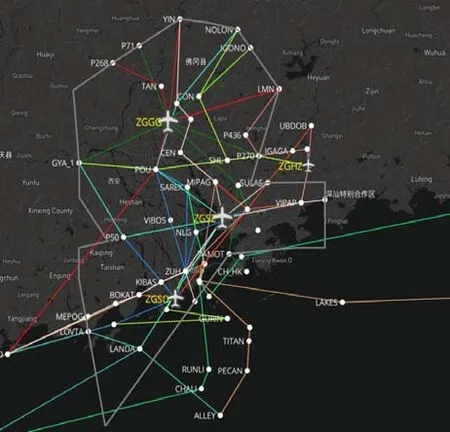
图2 大湾区机场群空域图Fig.2 Airspace of multi-airport system in the Greater Bay Area

本文选取粤港澳大湾区机场群，以及广州白云国际机场（ZGGG）、深圳宝安国际机场（ZGSZ）、珠海金湾机场（ZGSD）、澳门国际机场（VMMC）和惠州平潭机场（ZGHZ）为研究对象。因目前香港机场（VHHH）的航班运行基本上与内地几个机场的运行相互隔离，因此本文暂未考虑香港机场。

（2）机场和航路点公布容量。大湾区内各个机场公布容量由空中交通管制单位提供，如表1所示（单位：架次）。湾区外机场容量设置为无限量。模型中的关键航路点和容量均由管制员根据经验给出，关键的航路点包括MIPAG、LMN、GYA、YIN、TEPID和NOLON。

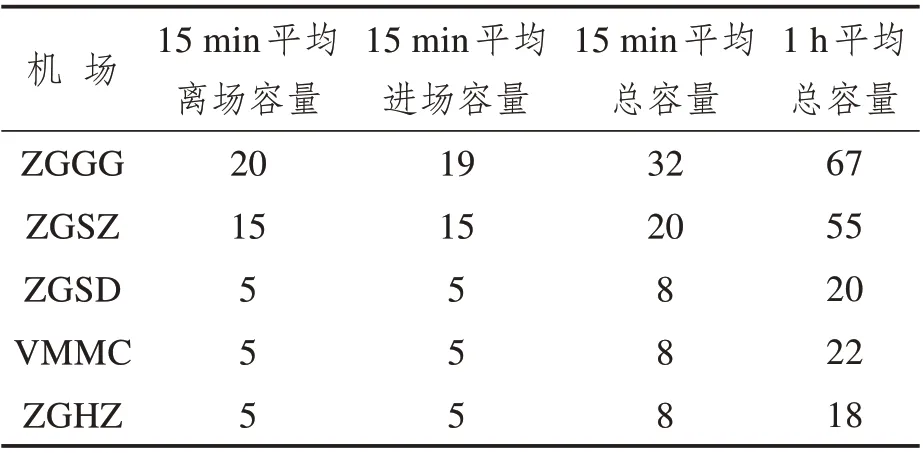
表1 机场容量Tab.1 Airport capacity

（3）飞行时间。航班在机场和关键航路点之间的飞行时间为2018—2019年历史飞行时间的中位值。

（4）AirTop 仿真模型。根据现行空域结构、运行规则等建立了AirTop 仿真模型。模型中的参数经过管制人员的确定，并通过实际运行场景进行了校正。因AirTop 仿真模型的构建并不在本文研究范围，所以在此不做过多描述。

（5）优化策略。根据运行单位意见，本文提出了三种优化策略，并设立了九个方案，如表2所示。因ZGGG和ZGSZ在机场群航班占比最大，故在优化策略二中均考虑两机场。在每种优化方案中，仅优化对象中机场的航班，其他机场的航班不进行调整。

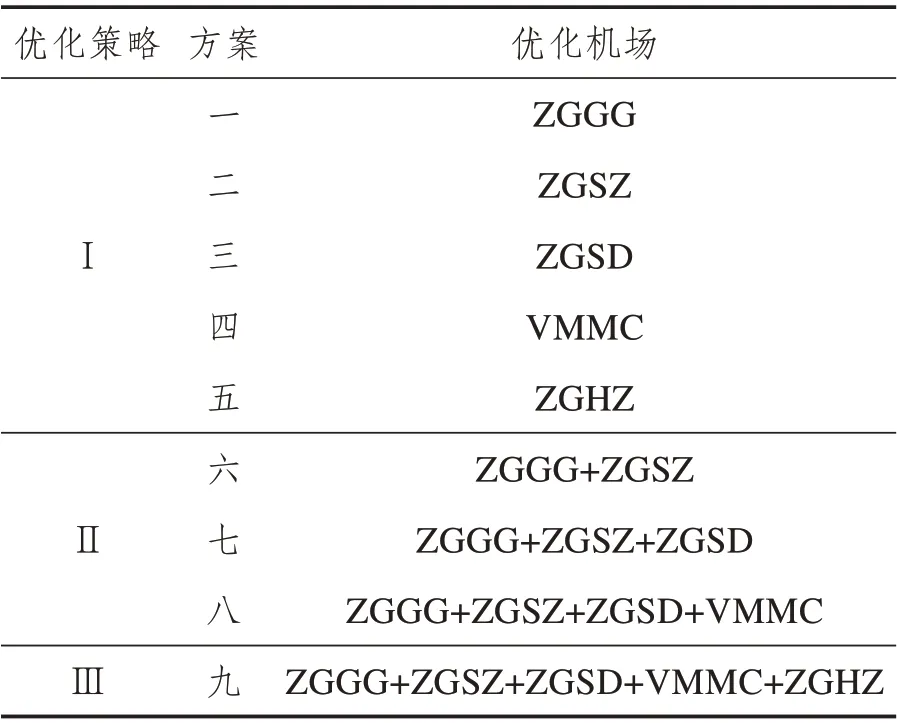
表2 九大方案Tab.2 Nine schemes

2.2 优化结果

九个方案下优化结果如表3所示（时刻调整单位：5 min；航班延误单位：min）。其中时刻调整为机场航班时刻调整总量，单位是5 min。延误减少量为优化后航班时刻表对比优化前航班时刻的延误减少值，航班延误为负表示航班延误增加。

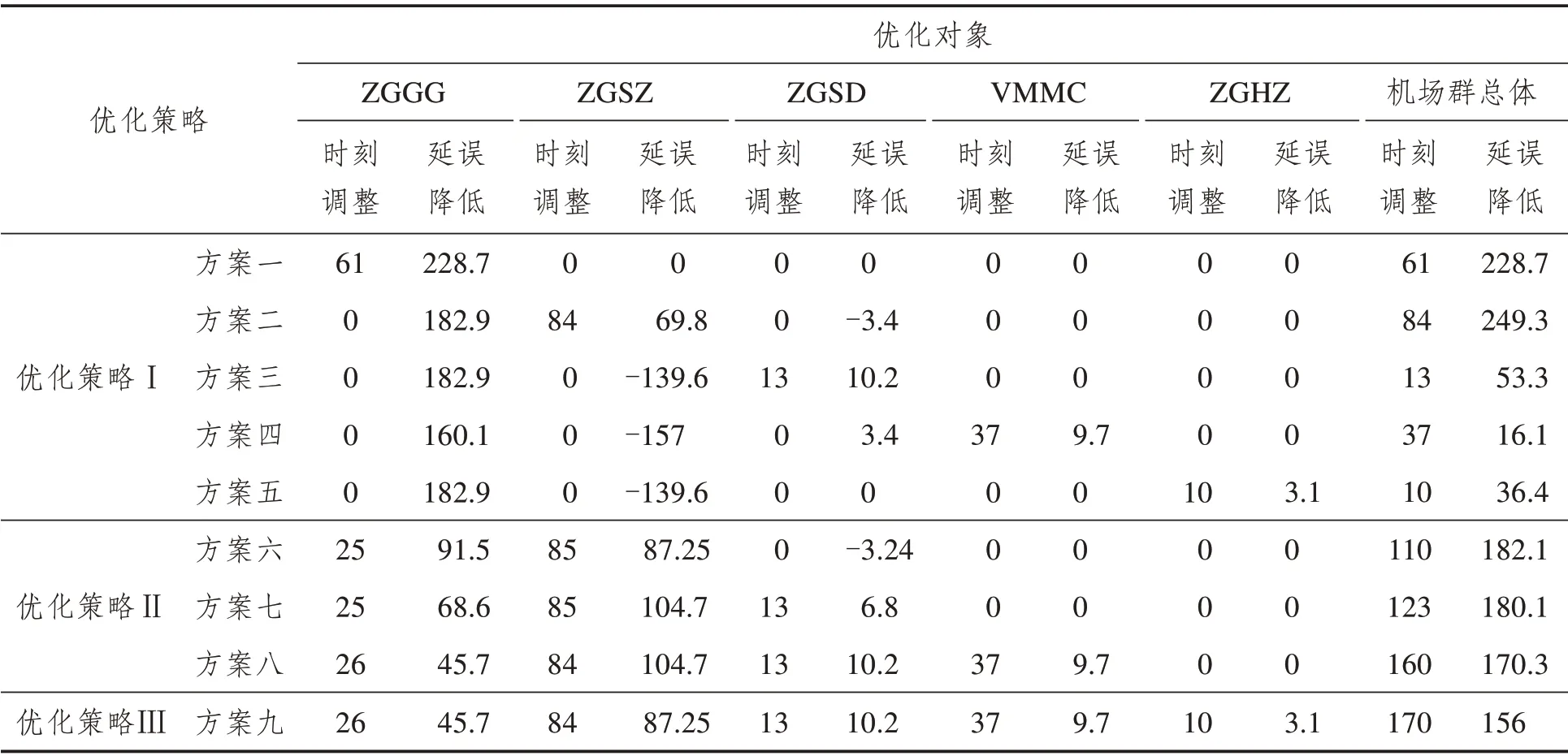
表3 各机场不同方案下优化结果Tab.3 Optimization results under different schemes for airports

2.2.1 时刻偏移情况

在优化策略Ⅰ中，ZGGG 和ZGSZ 整体航班调整量最大，主要原因是机场的航班多，且对大湾区机场群影响较大。ZGSD、VMMC、ZGHZ 因其航班量小，航班时刻调整细微，对机场群整体影响小。

在优化策略Ⅱ中，除了ZGGG 调整量由61 下降到25/26 之外，所有机场的调整量和单机场调整量基本相同。机场群时刻优化模型中需要考虑空域资源约束，因ZGGG 和ZGSZ 航班数量多，所以占用了大多空域资源。其中，ZGSZ 和机场群内其他机场共用多个航路点资源。ZGGG 和ZGSZ 的航班需求会导致MIPAG 的航路点超出容量，在ZGSZ 调整后，MIPAG 的流量满足容量约束，因此ZGGG经过此点的航班不再需要调整，所以ZGGG调整量下降。在优化策略Ⅰ中，ZGSD、VMMC、ZGHZ 进行单独优化调整时，TEPID、NOLON 这些共用航路点已经被ZGSZ 和ZGGG 航班占满无法调整。因此，在这些机场的单机场方案中主要调整的航班是导致自身机场流量超出容量的航班和导致航路点流量超出容量的航班。在多个机场优化方案中，ZGSD、VMMC、ZGHZ 三个机场同样调整上述航班，无法调整的航班已经由ZGGG和ZGSZ调整好。

对比以上三种优化策略中各机场平均调整量，以策略I 的时刻偏移最小，但策略Ⅰ中存在目标机场之外机场延误上升，特别是调整ZGSD、VMMC 和ZGHZ 的航班时，有可能造成深圳机场航班延误上升。优化策略Ⅱ和Ⅲ中，虽然目标外的机场延误未上升，但为了使各个机场延误下降，需要调整更多的航班。

2.2.2 航班延误情况

从仿真结果来看，各方案下目标机场的延误值较优化前航班时刻表均有所下降，机场群整体平均延误也较优化前降低。其中以策略Ⅰ中大流量单机场调整延误下降量最多，策略Ⅱ组合机场次之，策略Ⅲ整体机场调整延误下降量最少。组合机场随着可调整机场数量上升而延误下降量减少。

单机场方案中，ZGSZ、ZGSD、VMMC、ZGHZ的机场优化均会导致其他机场的延误增加。虽然整体延误和目标机场延误下降，但因只调整目标机场航班，导致机场群共用航路点拥堵，造成航班延误上升。ZGSZ 方案中，优化后ZGSD 的航班平均延误值较优化前上升，ZGSD 延误降低了5.4%；VMMC 方案中，ZGSZ 的航班平均延误值会较优化前上升，ZGSZ 的延误降低了10.4%；ZGHZ 方案中，ZGSZ 的航班平均延误值较优化前上升，ZGSZ的延误降低了9.4%。

在策略Ⅱ和策略Ⅲ优化方案中，虽然调整量基本相同，但其延误减少量不相同。在策略Ⅱ中，方案六中ZGGG 相比于单机场方案延误增多了，但ZGSZ 较单机场方案延误减少。方案七中，ZGSD 的延误相对单机场方案有所增加，但ZGGG和ZGSZ 的延误相对单机场方案降低。在四个机场的优化方案中，除了ZGGG 外，所有机场延误相对单机场优化方案均有所降低。策略Ⅲ中延误减少量最小，相比于方案一单机场优化，ZGGG延误量减少量80%，ZGSZ 延误降低量为25%，方案九中ZGSD、ZGHZ、VMMC 和单机场优化结果相同。策略Ⅱ与策略Ⅲ中调整目标的机场延误减少量基本相同。

2.2.3 时刻偏移与航班延误对比

定义α为平均延误减少量和时刻偏移的比值，以评估各个优化方面的优劣，即：

式中：dlk为k机场每个航班的平均延误减少量；adjk为k机场的时刻偏移量。

根据定义可知，α 为单位时刻偏移带来的延误降低效果。九个方案的各机场α值如图3所示。

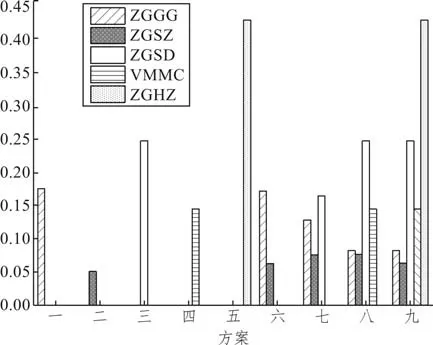
图3 九种方案下机场α值Fig.3 Airport alpha values under nine schemes

由图可知，组合机场方案的小流量机场（VMMC和ZGHZ）的α值均不小于其他方案中机场α值。优化策略Ⅰ中，ZGGG 的α相对于策略Ⅱ和Ⅲ更高，说明优化广州机场能够大大降低广州机场本场延误。ZGSD 所得的α值小于在方案七组合方案中的α值，而ZGSD 在方案三中的α值与方案一中相同。其中，α值变化最为明显的是ZGGG 和ZGSZ，因这两个机场在机场群中航班量是最大的，产生的延误也是最多的。在策略Ⅱ和策略Ⅲ中，ZGGG时刻的调整导致大流量机场延误调整效果变差。而ZGSZ 因为和其他机场共用航路点较多，随着机场可调航班整数量增加，其航班调整效果会更好。其中策略Ⅲ中ZGSZ 的α相对方案八机场低的主要原因是，ZGSZ 和ZGHZ 共用航路点少，为了满足ZGHZ 的延误下降，ZGSZ 的航班调整效果降低。

综合比较，策略Ⅰ单机场调整虽然目标机场平均延误会下降，且大流量机场延误下降最多，但其容易导致其他机场的延误上升，主要是在优化航班时存在部分航路点无法调整优化，而组合机场在调整时能将有效解决这个问题。组合机场方案调整量和单机场方案相同，ZGGG偏移量下降其延误上升，其他机场延误均下降。而随着目标优化的机场数量增加，机场群总延误值却增加。从调整效果来看，策略Ⅱ和策略Ⅲ的调整效果相近，ZGGG在方案六中调整效果更好。

2.2.4 机场群空域分析

大湾区的机场群空域复杂，不同机场的航班共用多个航路点。ZGGG 和ZGSZ 在GYA 和MABAG两点流量较大。在单机场方案中，为了满足这两点的容量约束，ZGGG的航班需要进行大幅度时间调整，故单机场ZGGG 调整量较组合机场大。在组合机场方案中，ZGSZ 能对经过MABAG的航班调整后，MABAG 容量得以满足，无须对ZGGG 进行调整，故ZGGG 航班调整数量下降。图4(a)为策略Ⅲ中MABAG 航路点15min 容流图，图4(b)为策略Ⅲ中GYA航路点15min容流图，可以看出，优化后的航班流量完全满足容量约束，且ZGSZ、ZGSD、VMMC 共用TEPID 航路点。在组合机场调整方案中，优化后航路点容流量更加平稳，可调整航班更多。图4(c)为策略Ⅲ中TEPID航路点15min 容流图，图4(d)为YIN 航路点15min 容流图。综上可知，由于可调航班增加，所以策略Ⅱ和策略Ⅲ对于航路点的优化更加灵活。

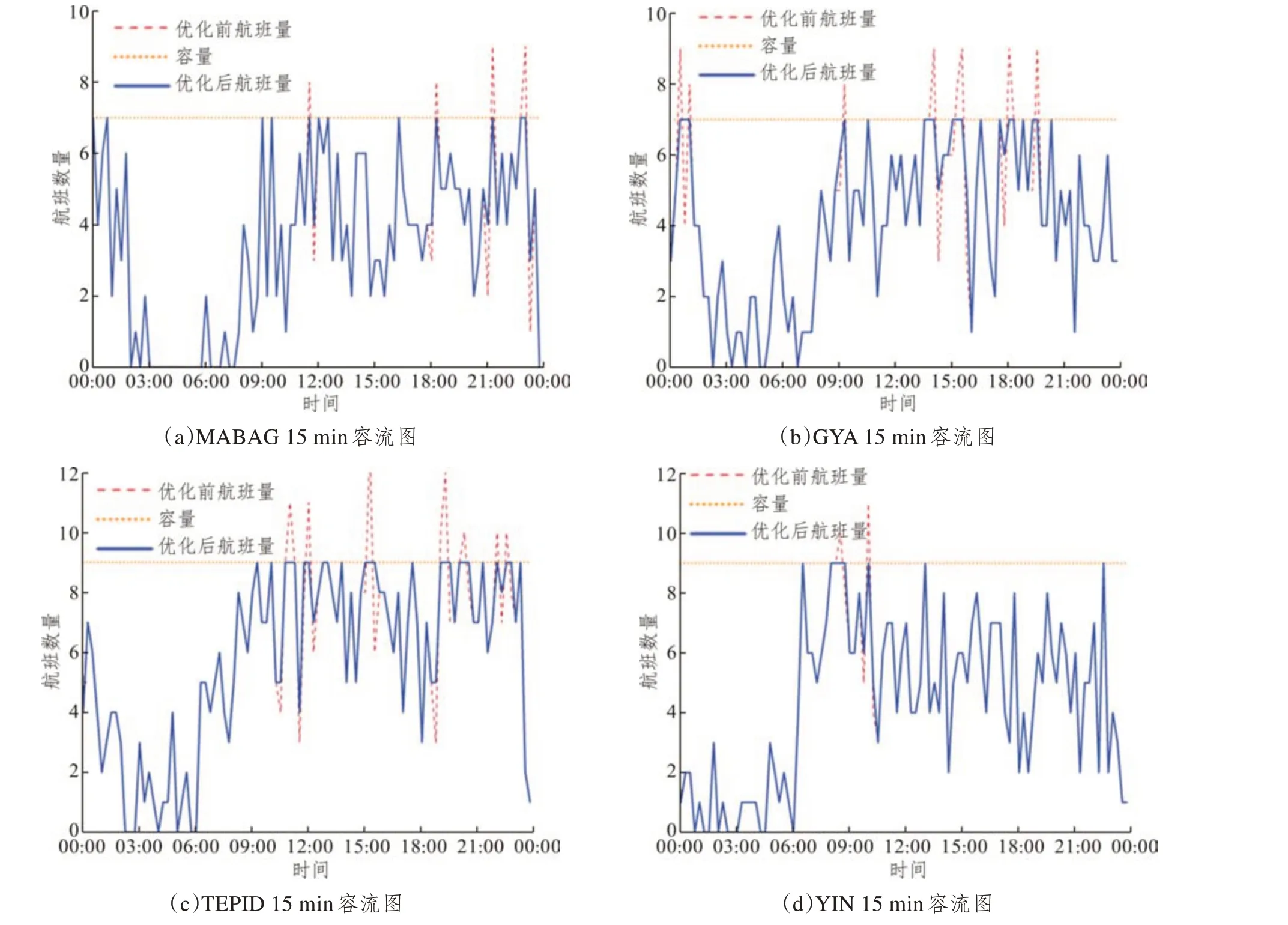
图4 策略Ⅲ航路点容流图Fig.4 Strategy Ⅲwaypoint capacity-flow chart

2.2.5 机场群航班时刻优化方案对比

分析以上三种优化策略结果发现，策略Ⅰ中ZGGG 和ZGSZ 单机场优化的总延误减少量比策略Ⅱ和Ⅲ中减少量更多。其中，ZGSZ 单机场优化后ZGGG 延误量也会下降，但ZGSD 的延误会增加。在策略Ⅱ中，ZGGG 和ZGSZ 联合优化方案相对于策略Ⅰ中ZGGG 的航班调整量减少了59%，其延误减少量相对减少了20.4%。但在策略Ⅰ中，单优化ZGSZ 会导致ZGSD 航班延误上升，单优化ZGSD、VMMC、ZGHZ会导致ZGSZ延误上升。

对比策略Ⅱ和策略Ⅲ可知，策略Ⅱ中ZGGG和ZGSZ同时优化方案相比策略Ⅲ，延误下降量多了16.8%，但偏移量少了35.3%。方案七中延误下降量比策略Ⅲ多了15.5%，调整量少了27.6%。方案八中延误下降量比策略Ⅲ多了9.2%，调整量少了5.9%。可以看出策略Ⅲ总延误减少量不如策略Ⅱ的组合方案，说明组合机场的延误降低效果更好。但采用策略Ⅲ优化后，机场群各机场的平均延误都下降了。

因此，单机场优化对于目标机场带来的效果好，但可能会导致其他机场延误增加。机场组合优化（策略Ⅱ）较之机场群整体优化（策略Ⅲ），目标机场航班延误下降的更多，但其他机场延误变化不大。策略Ⅲ中，考虑所有机场进行优化，因此各个机场的航班延误都有不同程度的下降。通过对航班偏移量分析可知，在机场群中优化大流量机场相对小流量机场的时刻偏移量更多，而且其时刻偏移带来的效果更好。将大流量机场组合作为优化目标，小流量机场也有可能延误下降。

3 结 论

本文在考虑到机场群运行特征、空域结构、容量限制、航班周转时间的基础上，建立了机场群航班时刻优化模型。模型最大限度减少航空公司请求偏移的同时，满足了机场容量和空域容量限制。为了探讨不同机场组合作为航班时刻优化目标对运行的影响，构建了单机场、机场组合和机场群整体为优化对象的三种优化策略、九种优化方案，通过AiTop仿真计算优化前后航班的延误情况。

研究结果表明：（1）机场进行单独优化时，目标机场的航班延误会大大降低，但是其他机场的延误可能会增加；（2）在机场组合优化方案中，以两个主要机场作为优化目标时延误降低效果最好；（3）在对机场群所有机场进行同时优化时，虽然所有机场各自的延误下降了，但机场群的总延误相比于机场组合优化效果不明显。主要是因为需要优化的机场增多，为了使小流量机场延误下降，牺牲了大流量机场在共用航路点高峰时刻的优化效果，导致整体延误升高。

本文的研究还存在一定的局限性，如仅以航班时刻偏移和航班延误进行了分析，并未考虑航班时刻偏移成本和航班延误成本。因此，下一步研究可考虑时刻偏移成本和延误成本，建立一个战略时刻优化和战术延误优化一体的模型，对时刻偏移和航班延误进行同时优化。本文研究为航班时刻管理部门提供理论依据和方法，时刻管理部门应综合考虑机场战略定位、航空公司需求和空域实际运行，选择合适的时刻配置方案，从而推进世界级机场的建设和运营。