面向恶劣天气的城市路网节点交通分配模型

尹玮奇，屈云超，吴建军

（北京交通大学，轨道交通控制与安全国家重点实验室，北京 100044）

0 引 言

随着经济的发展，人们出行需求逐步增加，在有限的道路供给资源条件下，交通拥堵时常发生。而恶劣天气会对道路的交通特征产生一定影响，使流量、速度随时间变化的波动增大，降低车辆运行速度和道路通行能力，增加交通事故发生的概率。据统计[1]，雨天是对我国道路交通影响程度较大的一种恶劣天气，由于城市现有排水设施能力不足，道路路面在强降雨条件下容易形成积水，增加车辆通行的风险，引发交通拥堵和延误，在积水严重时甚至会使交通中断，改变路网结构。因此，研究恶劣天气对城市道路交通运行的影响机理具有十分重要的科学意义。

目前越来越多的城市开始应用交通信息发布设施进行交通管理，在实际交通运行中可通过设置可变信息板、GPS 移动终端等方式来引导车辆运行，为交通控制策略的实施提供条件。研究恶劣天气下的城市交通网络演化特性和交通分配方法，对于提高路网特别是积水路段处的车辆运行安全性、完善智能交通系统具有重要的实用价值。

国内外学者结合实际天气、交通数据和现有交通流模型，已经对恶劣天气下的交通流特征进行了大量研究，但由于采用的模型和交通流数据采集地区的特性不同，计算得到的交通流参数也存在一定的差异[2-5]。而且，降雨强度越大、持续时间越长，更容易造成道路积水，对速度和通行能力产生的影响越大，从而增加车辆运行风险，影响车辆路径选择[6-7]。Etikaf 等人[8]校准和验证城市积水和交通微观仿真模型，模拟未来雨天情景下的交通运行情况，发现在降雨量较大、交通量较大时均存在较高的车辆延误；Ni 等[9-10]通过实验和模拟相结合的方法，研究雨天和道路积水对交通流量的影响，提出考虑雨天和积水对交通参数影响的传输模型，分析发现积水引起的道路密度增加更为显著。因此，在恶劣天气条件下道路的路面条件和运行特征会发生较大改变，需要对道路网络中断交通流动态演化过程进行进一步研究。

恶劣天气会影响交通网络的流量运行过程，其影响范围大、随机性强，对路网交通流的影响机理也较为复杂。特别是在雨天条件下，严重的路面积水会影响车辆安全运行，甚至阻断车辆通行，网络节点处积水路段的车辆运行安全不容忽视。目前有关恶劣天气下的城市网络动态交通数据样本较少，难以采用大数据的方法对路网的交通状态进行预测。因此，本文将研究恶劣天气下交通网络节点的流量分配特性，采用动态交通分配方法对交通网络运行状态进行建模仿真，分析恶劣天气下路网交通流演化过程。

动态交通分配模型是进行交通网络分析的重要方法之一，主要由路段模型和节点模型两部分组成。其中，路段模型描述了速度和密度、需求量和供给量之间的关系，节点模型描述了上游路段到下游路段的流量分配过程。元胞传输模型（Cell Transmission Model，CTM）[11]是一类经典的动态交通分配模型，目前已被广泛应用在交通路网的仿真、控制与管理中。在路段模型方面，现有研究中已根据经典的CTM 模型在元胞长度、连接方案、能力修正等方面进行了相应的改进[12-16]，以提高模型的计算精度。在节点模型方面，Tampère 等[17]定义了一阶宏观节点模型的通用公式，并提出了无信号和信号交叉口的模型实例；Smits 等[18]利用车头时距和转向延误进一步分析了节点交通流；Wright等人[19]提出基于FIFO 约束的节点模型推广形式，可应用于混合车流的流量分配；高明瑶等人[20]考虑道路流量对路阻的影响提出简化的节点分配算法、刘媛[21]对关键路段上的流量进行限制并设计了相应算法。

现有的节点模型难以描述恶劣天气下的路段通行特点，因此本文基于恶劣天气下的交通流特征对交通动态分配过程进行改进，通过分析交通运行中的车辆排队和延误现象，采用具有启动损失的元胞传输模型作为路段传输模型。在节点流量分配模型中添加积水路段优先通行的约束条件，进一步调整分配规则以及时疏散车辆、减少积水路段处的排队，建立适用于恶劣天气的交通分配模型，从而更好地体现受天气影响下的道路网络中的交通流演化过程并优化交通分配结果，为恶劣天气下不同控制目标的交通策略的改善提供科学依据。

1 受天气影响的路段交通流传输模型

1.1 元胞传输模型

元胞传输模型将模拟时间和道路路段分别进行时间和空间上的离散化，形成一系列具有相应路段通行能力与承载能力的元胞。交通流在路段上的传播基于上下游相邻元胞的密度、流量关系，通过元胞间的流量传输来体现。模型中自由流速度为vf，反向传播速度为w，路段最大通行能力为Qmax，临界密度为ρcr，阻塞密度为ρJ，时间步长为Δt。ρi(t)为元胞i在t时刻的密度，则t时刻元胞i的需求函数di(t)和供应函数si(t)如下两式：

1.2 受天气影响的改进元胞传输模型

在有信号控制的交叉口处，由于信号灯的变化会出现车辆排队通过交叉口的现象，队列前端车辆需对前方路段的路况做出判断，造成车头时距大于饱和车头时距，道路难以达到最大通行能力，即存在一定的启动损失。Srivastava[22]在元胞传输模型中通过线性递减函数代替原有需求函数，可以有效地体现启动损失对交通流传输过程的影响。而恶劣天气会降低道路附着系数和环境能见度[23]，增加驾驶员的反应时间，加剧交通流的拥堵，造成拥堵瓶颈处车辆的减速甚至停止，因此在无信号控制的路段也易产生排队现象和启动损失。同时，交通流参数和降雨量关系模型的拟合结果显示[23]，饱和车头时距、启动损失时间均与降雨量成正比，且启动损失时间对降雨量变化的反应更为敏感。因此在天气影响的条件下，可利用考虑启动损失的模型[22]对恶劣天气下路段交通流的传输过程进行分析。

根据已有研究结果[2-5]，雨天对自由流速度vf和通行能力Qmax的影响较大。为更好地描述恶劣天气下的交通流运行状态，需要对vf、Qmax等参数进行修正，修正前后的模型需求、供应函数如图1所示。

图1 考虑启动损失的元胞传输模型的需求、供应函数图Fig.1 Demand and supply functions of cell transmission model considering start-up loss

在模型中，引入达到阻塞密度时元胞的通行能力QJ来表述上游需求和下游供应之间的相互影响，并根据元胞需求利用式（4）、（5）计算出堵塞密度ρJ*、斜率u*：

式中：θ1、θ2分别为天气影响下自由流速度和通行能力的折减系数，δ为元胞所在路段通行能力受积水影响的折减比例。研究结果显示[24]，当积水深度小于15 cm 时，驾驶员能够控制车辆速度，以减少积水造成的影响；当积水深度在15～30 cm 时，驾驶员对速度的判断较为困难，为避免造成车辆熄火，以尽可能低的速度缓慢通过；当积水深度大于30 cm 时，车辆无法通行，道路中断。因此，δ的值随积水程度增加而减少(0≤δ≤1)，当积水造成道路中断时δ=0。

临界密度、反向传播速度相应地调整为w′、ρcr'，计算公式如下：

2 天气影响下的节点交通流量分配模型

道路网络是路段和节点的集合，节点包括有两个及以上路段的交叉口、匝道等，衔接了不同方向的交通流。Daganzo[25]描述了合流节点模型和分流节点模型：合流节点模型指两个路段同时连接到另一个路段的上游路段的模型，流入节点的各个路段的传输流量与路段间交通流的流量比例有关，影响下游路段可分配给该路段的供应量；分流节点模型指两个路段同时作为另一个路段的下游路段的模型，流出节点的各个路段可传输的流量受到上游车辆前往该路段的转向比例影响。

本文研究的节点模型包括合流和分流的多种情况，既适用于多条路段连接另一条路段、一条路段连接多条路段的节点，也适用于多条路段同时连接到其他多条路段上游的节点。假设节点不存储流量，t时刻从上游路段流入到节点的流量会立刻进入下游路段，上游路段流出的流量总和等于下游路段流入的流量总和，在合流和分流过程中考虑积水路段影响的通行优先级，对模型进行一定的改进与推广。即在明确节点处不同方向流入、流出量的基础上，进一步通过设置路段的通行优先级实现积水场景下的流量分配，上游路段的通行优先级根据路段传输模型中得出的需求量进行动态调整。在进行动态交通分配时，一旦确定了车辆出行路径也就确定了路段的流入率。由于在雨天天气下，部分路段可能会出现积水甚至造成中断，进一步影响通行能力，本文在建立节点模型时考虑到路段积水情况的限制，引入积水路段的优先级约束，进一步根据积水情况对路段流量分配的优先比例进行调整。道路积水越深，车辆通行风险性越高，因此设置更高的流量分配优先比例，从而实现积水路段处车辆的优先通行，提高车辆运行的安全性。其中，本文中的节点主要为城市道路网中的无信号交叉口和快速路匝道等，图2为节点示意图，该节点具有m个流入节点的元胞和n个流出节点的元胞。A为流入节点的元胞i的集合，即i∈A（i= 1,…,m），B为流出节点的元胞j的集合，即j∈B（j= 1,…,n）。

图2 节点示意图Fig.2 Schematic of nodes

2.1 基于元胞传输模型的节点交通分配模型

节点处交通流量分配的关键在于内部状态和边界条件，节点的内部状态影响节点模型的分配效率，通过元胞传输模型得到上下游路段的需求量、供应量，从而确定边界条件。当节点的下游路段供应总量无法满足上游路段的需求总量时，会发生拥堵情况，如何在维持交通正常运行的条件下合理分配供应量是节点交通分配模型需要解决的重要问题。根据实际交通网络的节点分配规律，任何一个路段的供应量只能提供给路径中经过该路段的车辆。在利用元胞将道路网划分的基础上，为得到更符合实际的流量分配结果，根据Tampère 等[17]提出的对一阶节点模型的要求，文中基于元胞传输模型的节点交通流量分配模型满足以下条件：

（1）非负性：所有流量都必须是非负的，t时刻元胞i中经过节点流入元胞j的流量为fij(t)，即fij(t)≥0,∀i,j,t。

根据以上目标和条件，结合基于路径的元胞传输模型[26]构建节点处的流量分配方法，将流入节点元胞中的交通流量按照路径进行拆分，使尽可能多的流量通过节点，之后将流量合并到集合B的元胞中，向下一个节点传输。图3为节点流量分配模型示意图。

图3 节点流量分配示意图Fig.3 Schematic of node traffic distribution

基于元胞需求量、元胞内的车辆数、车辆路径和所在路段、节点的内部结构，划分集合A中元胞的需求总量，元胞i中可流入元胞j的需求量dij(t)由下式计算：

当集合A中元胞的需求可以完全被满足时，t时刻由元胞i经过节点流入元胞j的流量fij(t)即为dij(t)。当这部分需求无法完全被满足时，fij(t)由元胞i中前往不同方向的需求量比例决定，因此fij(t)可由下式计算：

式中：hj(t)为在受天气影响时，利用考虑启动损失的元胞传输模型计算得到的t时刻元胞j的供应总量；ε为一个极小的正数。最终可得到t时刻元胞i流入节点的流量fini(t)和节点流向元胞j的流量foutj(t)。

2.2 考虑优先级的节点交通分配模型

在模型中需要对供应量进行重新分配，对于集合B中元胞j的供应量，如在满足所需要的优先流量后仍有剩余，则将剩余供应量重新分配给其他路径前往j的车辆，从而最大限度地利用节点处的传输能力，尽可能地满足集合A中的元胞需求总量。根据元胞所在路段状况的限制，利用优先级顺序进行流量分配，即优先分配给存在积水的路段，且在集合B中的元胞供应总量较充足时，积水路段的元胞传输量不少于根据优先比例λ分配时获得的流量。λ的值与路段积水程度有关（0≤λ≤1），但当积水造成中断时λ=0。通过进行天气影响下的交通仿真，可以获得为实现对路网进行交通控制所需的λ值。t时刻自元胞i经过节点流入元胞j的流量fij(t)需满足fij(t)≥min{λi⋅dij(t),hj(t)}，λi表示与元胞i所在路段状况有关的参数。图4为考虑优先级的节点流量分配模型示意。

图4 考虑优先级的节点流量分配示意图Fig.4 Schematic of node traffic allocation considering priority

t时刻，当元胞i所在的路段出现积水时（即0<λ），优先考虑该元胞上的流量在相关节点处的分配，自元胞i经过节点流入元胞j的需要进行优先分配的流量用fpij(t)表示：

式（11）、（13）～（15）共同构成了天气影响下考虑优先级的节点交通流量分配模型。

3 路网动态分配模型构建与分析

3.1 模型仿真方法

在各个需求时段，利用相继平均法进行多次迭代求解，从而实现对路径流量的更新。在迭代时，考虑启动损失的元胞传输模型和优先级的节点流量分配模型进行交通网络动态加载，获得各时刻的道路阻抗。本文在网络加载时将出行需求和传输流量离散为个体出行者，加载步骤如下：

步骤1 初始化交通网络，包括路段交通流参数、天气影响的折减系数、路网的动态出行需求、积水路段位置和折减比例、优先比例等，将路段划分为元胞的形式并初始化元胞参数。加载交通需求量，设置初始仿真时刻t=0，仿真总时长为T。

步骤2 根据考虑启动损失的元胞传输模型，利用式（7）对自由流速度、通行能力进行修正，基于路段交通流利用式（8）～（10）计算元胞需求量、供给量等，得到当前时刻各元胞内的可传输量。

步骤3 按照考虑优先级的节点流量分配模型，利用式（11）、（13）～（15）计算节点处各个方向中上游元胞向下游元胞的实际传输量。

步骤4 记录各路段的实际行程时间和自由流走行时间，更新路段交通流。

步骤5 更新仿真时刻t=t+1，进行终止条件判断，若t≤T则转入步骤2；否则停止，输出仿真结果。

3.2 场景设定

本文利用Nguyen-Dupius（N-D）路网来验证模型的有效性，路网包含13 个节点、19 条路段、4 个OD 对，其中节点1、4 为起点，节点2、3 为终点，如图5所示。设置路段自由流速度为90 km/h、70 km/h，道路通行能力为1 600 veh/h、1 400 veh/h，道路阻塞密度为120 veh/km、100 veh/km，阻塞通行能力设为最大通行能力的70%。将路段划分为元胞的形式，共获得60个元胞，相应得到各个元胞的交通参数。仿真时长T设为1 h，时间步长Δt设为6 s，各路段初始流量为0 veh，交通需求量每5 min 加载一次，OD 对（1,2）、（1,3）、（4,2）、（4,3）单次加载的需求量分别设为160 veh、120 veh、150 veh、200 veh。

图5 N-D路网拓扑图Fig.5 Illustration of N-D road network

不同路网受降雨影响的交通参数折减系数没有统一的研究结果，已有研究中[27]证明在强降雨天气下自由流速度下降6.4%至10.3%，通行能力下降5.7%至19.5%，本文利用北京市快速路的检测器数据进行模型拟合，得到自由流速度、通行能力折减系数分别为9.00%和13.70%。拟合结果符合该范围，因此以该值对考虑启动损失的元胞传输模型进行修正，计算各个元胞的需求量和供应量。根据全有全无的分配结果，将利用率较高的路段10设置为积水路段，为研究不同积水程度时的运行结果，将通行能力受积水影响的折减比例δ设为0.3、0.4、0.5、0.6，优先比例λ分别设为0.3、0.5、0.7、0.9。

3.3 路网运行评价

由表中可以看出，在不同积水程度时，设置优先级后分配到路段10 上的交通量均有所减少，同时路网的平均行程时间和拥挤延迟也有一定程度的下降。在不同优先比例条件下，路网的运行状态存在差异。在δ=0.3 情况下，当λ=0.7 时积水路段10分配的交通量最小，为687 veh，此时Tˉ、T͂的值也最小，分别为18.12、7.06 时间步；在δ=0.4 情况下，当λ=0.3 时路段10 获得最小交通量748 veh，λ=0.9时获得最小Tˉ和T͂分别为18.19和7.22时间步；在δ=0.5 情况下，当λ=0.3 时路段10 获得最小交通量880 veh，λ=0.7 时获得最小Tˉ和T͂分别为18.43 和7.46 时间步；在δ=0.6 情况下，当λ=0.7 时路段10 获得最小交通量1081 veh，且最小Tˉ和T͂分别为17.63和6.69时间步。

仿真时段内路段10 的交通分配量变化如图6所示，由图可看出在前三次加载中该路段的交通量波动较大，路段交通分配量与仿真中设置的优先比例密切相关。因此，当恶劣天气下交通控制的目的不同时，应设置不同的优先比例。如在δ=0.4时，以积水路段的交通量最小为目的时，λ可设置为0.3，以路网平均运行时间最小为目的时，λ可设置为0.9。

图6 不同参数下路段10分配量变化图Fig.6 Load-dependent distribution of link 10 under different parameters

在不同模型下设置的积水路段10密度随仿真时间的变化如图7所示，由图可以看出在模型没有设置优先级时，δ=0.3 时在300 时间步后路段10 处于拥堵状态且拥堵无法消散；δ=0.4 时在150 时间步后路段即处于拥堵状态；δ=0.5 时在100 时间步后处于拥堵状态，持续到350时间步时有一定缓解但随后又出现拥堵；δ=0.6 时在150 时间步后出现拥堵，在250 时间步后消散。在不同δ的情况下，路段的拥堵状况受优先比例λ值的影响存在差异，同一λ值下δ的不同也会影响路段在仿真时段内的运行状态变化。在δ=0.3 情况下，当λ为0.3 时在300 至400 时间步内有拥堵产生，后逐步消散；当λ为0.5时，在350至400时间步内有拥堵产生，相比λ为0.3时持续时间较短；当λ为0.7和0.9时无拥堵产生。在δ=0.4情况下，当λ为0.3时在150时间步后有拥堵产生，持续至300时间步后开始消散；当λ为0.5时在230 时间步后有拥堵产生，至350 时间步后开始消散；当λ为0.7 和0.9 时无拥堵产生。在δ=0.5情况下，当λ为0.3时在100至400时间步内处于拥堵状态；当λ为0.5时在300至450时间步内处于拥堵状态，拥堵出现的时间延后且持续时间有所减少；当λ为0.7 时在200 时间步后处于拥堵且仅持续至300时间步；当λ为0.9时无拥堵产生；在δ=0.6情况下，当λ为0.3 时在150 时间步后存在一定拥堵，约持续50 个时间步后消散；当λ为0.5 时，在180 时间步后存在拥堵，约持续70 个时间步后消散；λ为0.7、0.9时无拥堵产生。在设置的多个优先比例下积水路段的运行状态均有较大改善，因此，积水路段的运行状态受优先级影响，在一定范围内，适当调整优先比例可以有效减轻路段的拥堵情况，提高车辆运行安全性。

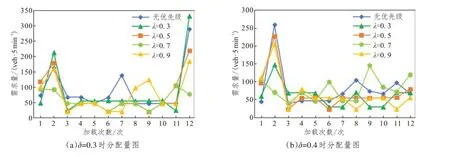
图7 不同参数下路段10密度变化图Fig.7 Time-dependent density of link 10 under different parameters

3.4 控制目标下的路网分配结果

以δ=0.4的场景为例，根据表1结果可知，控制目标为积水路段在仿真时段内通过的交通量最小时，在有优先级的模型中λ可设置为0.3，控制目标为路网平均运行时间最小时，λ可设置为0.9。利用不同模型进行动态分配后路网中各路段的交通量如表2所示。

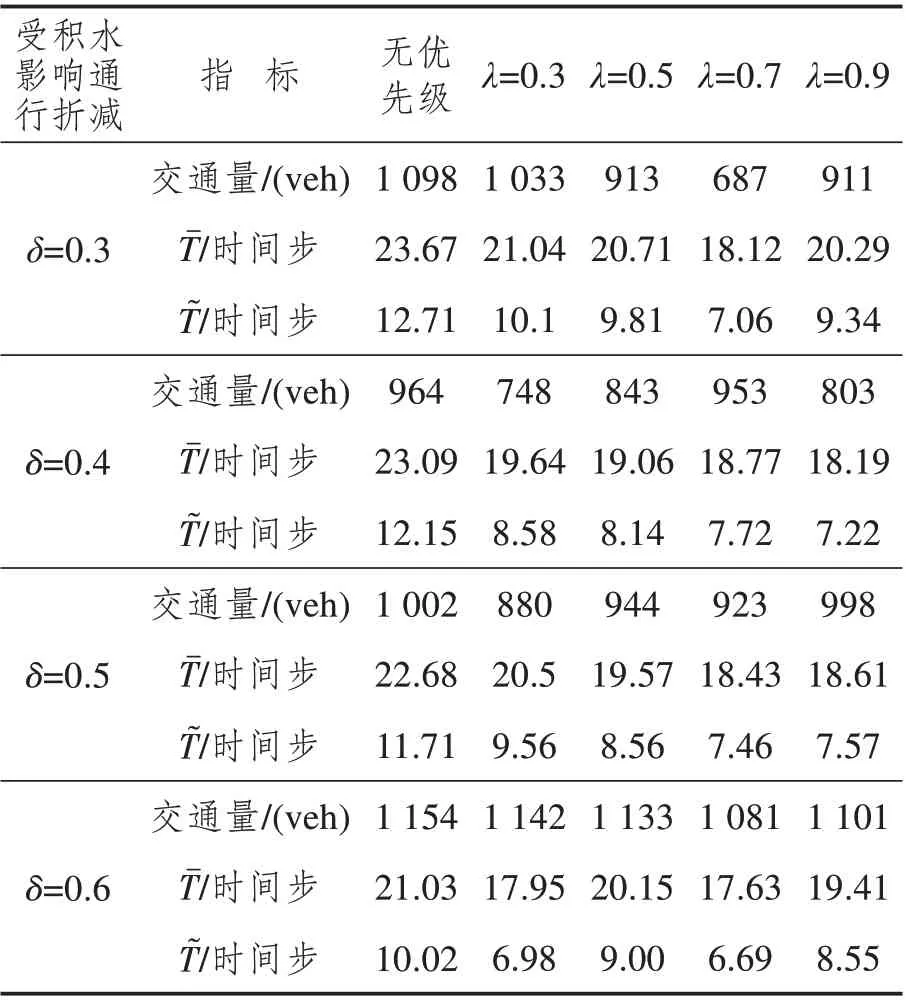
表1 路段10积水时路网运行指标结果Tab.1 Results for road network operation indicators when section 10 is flooded

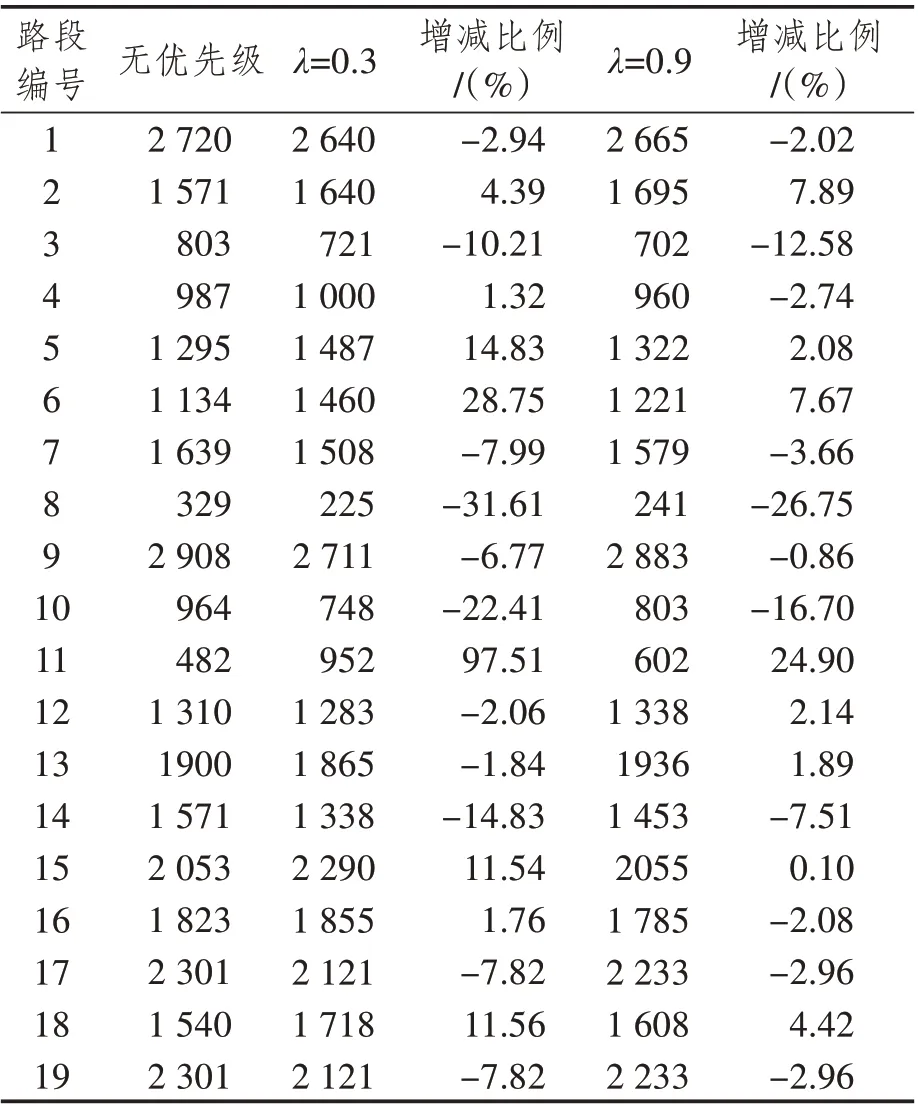
表2 不同模型下路网交通分配结果Tab.2 Traffic allocation results for road networks of different models

由结果可以看出，在λ=0.3 时，设置的积水路段10在有优先级模型下的交通分配量比无优先级模型减少了22.41%。由图5 的路网拓扑结构可知，路段10 的车辆自路段3、5 流入，从路段14、17流出。路段3、14、17的交通分配量分别减少10.21%、14.83%、7.82%，路段5 的交通分配量增加14.83%。路段6、11 的交通分配量增加较大，分别为28.75%、97.51%，即选择路段6、11所在路径的车辆增加。这与实际交通运行规律相符合，当路段通行受阻时，后进入路网的车辆会选择其他与积水路段关联较小、行程时间较短的路径行驶。根据表1 可 得，路 网 运 行 的Tˉ降 低17.45%，T͂降 低33.03%，有效地减少了行驶时间和等待时间。在λ=0.9 时，路段10 的交通分配量减少16.70%，路段3、14、17 的交通分配量分别减少12.58%、7.51%、2.96%，路 段5、6、11 的 交 通 分 配 量 分 别 增 加2.08%、7.67%、24.90%，与λ=0.3 时交通变化规律相似，但变化程度较小。路网运行的Tˉ、T͂分别降低21.19%、40.62%。

以λ=0.3、0.9 的情况为例分析仿真过程中路网交通拥堵状态的变化情况，拥堵程度判断标准如表3。Cd表示路段实际车辆数与路段最大承载车辆数的比值，当Cd≥0.6 时认为该路段存在拥堵。无优先级模型下在不同时间步时路网交通拥堵状态如图8 所示，由图可以看出，在第200、500时间步时路段5、10均处于轻度拥堵状态，这与图7 的分析结果一致，路段3 从轻度拥堵变为基本畅通。优先比例设置为0.3、0.9 时第500时间步的运行结果如图9 所示，对比可知设置优先比例后路段3、5、10 上的拥堵在运行过程中逐渐消散，该时刻路网中均无拥堵点。因此利用有优先级的模型进行分配后在一定程度下可以促进路网的畅通，特别是在无优先级模型下积水路段拥堵严重时，通过设置优先级能更为有效地改善路网的拥堵情况。

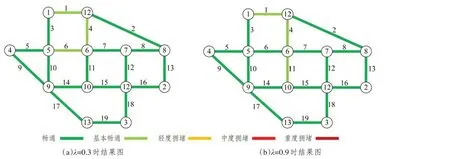
图9 有优先级模型下第500时间步路网拥堵状态Fig.9 Congestion status of road network with priority model at 500th time step

表3 路段交通拥堵程度判断标准Tab.3 Judgment criteria of traffic congestion degree of road section

图8 无优先级模型下路网拥堵状态Fig.8 Congestion status of road network using no-priority model

根据表2的分析结果可知，设置优先级后路段6、11 分配的交通量有较大增加，在不同模型下的路段密度随时间变化如图10 所示。由图可以看出，λ=0.3 和λ=0.9 时路段6 密度变化趋势较为相似，在350 时间步后路段密度较低，相比无优先级时拥堵情况有所改善。虽然路段11分配的交通量增加，但在仿真过程中仍处于较为通畅的状态。因此，本文建立的考虑优先级的节点流量分配模型能够通过调整车辆路径将交通量分配到其他路段中，在改善该路段拥堵情况的同时维持其他路段的交通稳定。

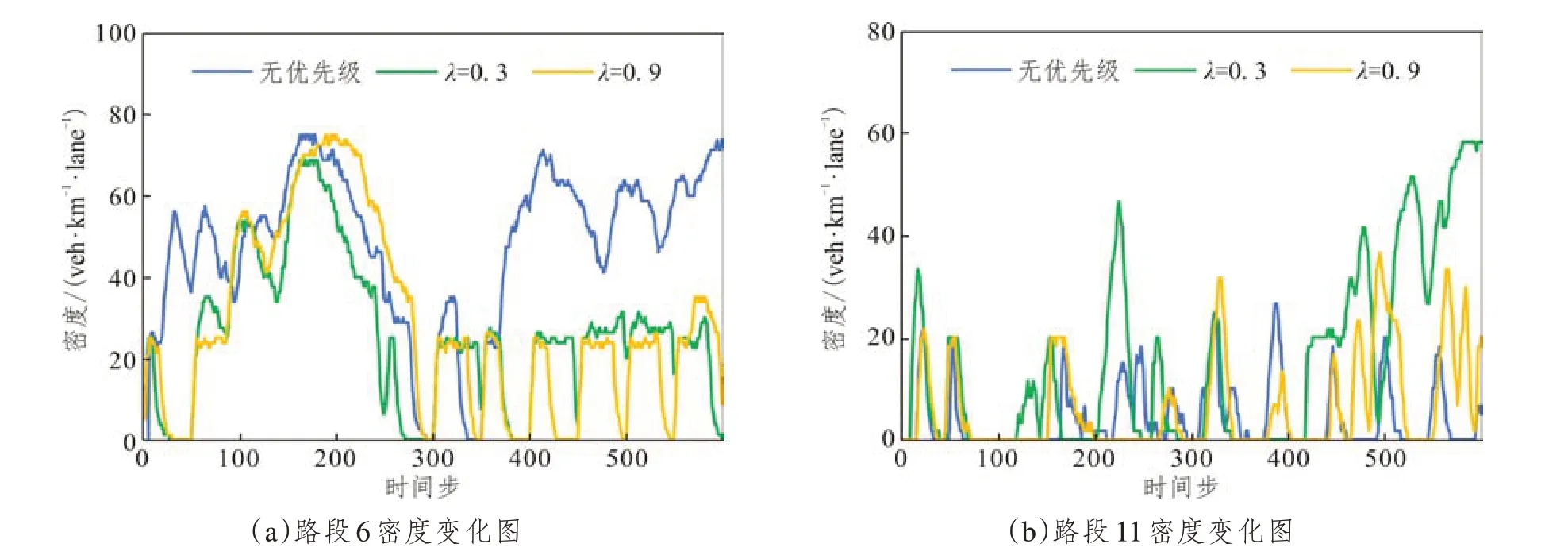
图10 不同模型下路段密度变化图Fig.10 Time-dependent link densities under different parameters

3.5 多条积水路段下的路网运行结果

在实际降雨场景中，降雨天气会同时影响多条道路的通行状况，因此将积水道路的设置扩大到路段6、10、14，同样以δ=0.4 为例对不同优先比例下的路网运行情况进行分析。此时路网运行指标结果如表4所示。

由表4 可以看出，λ=0.7 时Tˉ、T͂的值最小，分别为22.99、12.09时间步。仿真时间内设置的积水路段密度随时间变化如图11所示。由图可以看出设置优先比例后三条积水路段的密度峰值均降低，拥堵时长也有所下降，在仿真时段内路段6的拥堵时长比例由33%下降至0.67%，路段10由66.5%下降至无拥堵产生，仍能起到改善积水路段拥堵状况的效果。

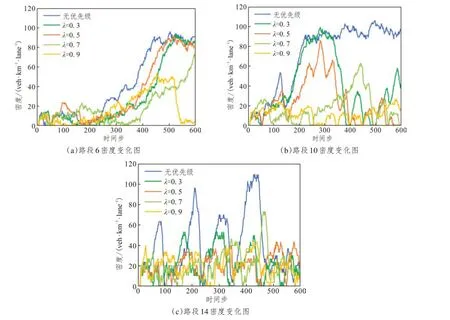
图11 不同模型下不同路段密度变化图Fig.11 Time-dependent link densities under different parameters

表4 多条积水路段时路网运行指标结果Tab.4 Results for road network operation indicators when multiple sections are flooded

仿真过程中路网交通拥堵状态的变化情况如图12 所示。在无优先级模型下，运行至第500 时间步时路网存在较严重的拥堵，其中路段5、6、9为轻度拥堵，路段10 处于中度拥堵。在λ=0.7 时，同一时刻仅路段5处于轻度拥堵，其他均为畅通或基本畅通状态，处于拥堵状态的路段数量明显减少且拥堵等级相对较低。因此，在设置路网中部分区域内为积水路段时，利用有优先级的模型进行分配后仍可以起到减轻路网拥堵的效果。

图12 第500时间步路网拥堵状态Fig.12 Congestion status of road network at 500th time step

4 结 论

本文基于恶劣天气以及积水对交通流量的影响，构建考虑分配优先级的节点流量分配模型，进行路网的动态交通分配，进一步实现恶劣天气下的交通管理。主要研究成果和结论如下：

（1）结合考虑车辆启动损失的元胞传输模型，基于天气对道路交通流特征产生的影响对相关参数进行修正，使模型更适用于描述天气影响下的路段交通流传播过程。根据天气导致道路通行能力改变的程度，针对道路积水造成通行能力下降甚至中断的情况调整分配的优先级，建立节点处的流量分配模型，用以描述恶劣天气下的路段优先通行特性。

（2）结合修正后的元胞传输模型在路网中进行单条路段积水和多条路段积水场景下的交通仿真，分析交通动态分配和路网运行过程。在不同积水程度、优先比例条件下积水路段分配的交通量均有所减少，拥堵状态也有所改善，同时没有对其他路段的交通状态造成破坏，且在适当范围内调整优先比例能够优化积水路段的运行状态。

（3）本文建立的模型在单条路段积水和区域内多条路段积水的情况下均有一定的适用性，能够在一定程度上减少路网中特别是积水道路的车辆延误时间，得到较优的动态交通分配结果。通过该模型能够推演不同优先比例的控制策略下路网交通流的演化过程，在一定程度上提高积水路段的通行效率和安全性。

在今后的研究中，如何根据不同天气场景、不同交通控制目标合理调整模型的优先比例，提出更高效的控制策略，是一项重要的研究内容。同时，考虑恶劣天气对交通需求产生的影响，深入分析研究恶劣天气下的出行行为变化，更精准地描述路网交通流的演化过程。此外，未来的车路协同、信息全覆盖等智能交通场景能够为节点处流量分配控制提供新的条件，通过结合个性化诱导的方式进一步提高控制效率，为城市道路智能交通诱导系统提供决策支持。