双向双车道公路超车行为的演化博弈分析

岳全胜，冯忠祥，李靖宇

（1.合肥工业大学，汽车与交通工程学院，合肥 230009；2.合肥工业大学，土木与水利工程学院，合肥 230009）

0 引 言

双车道公路是我国交通网络中的重要形式，在保障农村和城镇居民出行，促进地方县镇农村的交流中起到重要作用。根据公安部发布的报告，不当超车已成为农村道路事故中的重要原因[1]。交通安全造成的人员伤亡和财产损失严重[2]，交通形势严峻。超车是一项复杂的任务，同时亦伴随着高风险。德国的73 916 起交通事故中，有6%是由于超车造成的，导致了9%的伤亡[3]。印度的超车事故占道路交通事故总数的7.3%，其中7.8%是道路死亡事故[4]。美国有近3.3%～4.5%的驾驶人报告危险驾驶的主要表现是不当超车[5]。双车道公路超车行为往往伴随着更高的碰撞风险，Choudhari 等[6]认为，在未分割的双车道道路上超车是对驾驶人驾驶认知要求最高和最具挑战性的任务之一。驾驶人在双车道超车时需要借对向车道行驶，危及前车以及对向车道车辆的行车安全，从而产生侧滑碰撞和迎面碰撞的可能性很高。因此分析驾驶人的超车心理以减少不当的超车行为对避免碰撞事故尤为重要。

近年来，国内外研究人员对超车行为进行了大量研究并取得了一些成果。Pawar等[7]将跨越车道线时间和速度变异系数作为解释变量，基于参数化生存分析和广义线性混合模型，探究了时间压力与超车行为的关系。Soni 等[8]利用激光雷达和摄像机采集了印度双车道公路的超车行为的数据，分析了超车方和前方车辆的车辆类型对超车时间的影响。Figueira 等[9]基于模拟器统计了640组超车行为数据，探索了前方车辆的速度和类型对超车行为的影响。Kinnear 等[10]基于183 名公众对剪辑过的驾驶视频的反馈，通过混合因素方差分析研究了前车速度、交通量、前方车辆数等对超车意图的影响。戢晓峰等[11]通过构建超车行为变量指标体系，建立基于生存分析的山区双车道公路超车持续时间模型，确定了影响因素与超车持续时间之间的关系。陈雅君等[12]以高速公路为背景，针对超车模式构建模型，验证了安全运行区域模型的稳定性和准确率。张文会等[13]提出了一种双车道公路超车安全距离模型，得出超车车辆与前方车辆及对向车辆之间的临界安全距离图。唐夕茹等[14]将驾驶人特性与车辆动力性能引入元胞自动机模型，建立了改进型双向双车道元胞自动机模型，结果表明流向比与交通冲突次数显著相关。荣建等[15]将超车过程分步骤划分来建立超车模型，通过仿真实验得到了超车率和交通流量之间的关系。

上述研究成果为双车道公路上的超车行为研究奠定了一定的基础，但较少学者对目标车辆以及超车车辆的心理决策过程展开详细分析，从不同心理认知角度揭示驾驶人在超车过程中的心理变化机制。由于双车道公路的特殊性，超车过程受到前方车辆、后方车辆以及对向车道车辆的影响，对向车道车辆的位置不同亦会对各角色驾驶人的决策产生影响，此种情况较为复杂。因此在本文中主要研究同方向前、后车的决策行为。对向车道来车对超车行为产生的影响，本文将以问卷调查的方式，由受访者基于主观感受进行评价。在这种情况下，超车车辆完成超车需要目标车辆减速让行，强行超车会导致巨大的碰撞风险。但目标车辆减速让行，势必会增加自身的出行时间成本。显然，目标车辆和超车车辆的行为是相互影响的，二者均试图选择一种能够获得最大收益的策略，这体现了典型的博弈行为的特点。传统博弈论认为所有的参与者都是完全理性的，且是在完全信息的条件下进行的，这种假设不符合真实的情境。随着博弈论的发展，Smith 等[16]综合了经典博弈论和生物进化论的特点，提出了演化博弈理论。演化博弈论是研究长期动态博弈的有效方法，它通过分析有限理性参与者和博弈的动态过程，克服了传统博弈论的缺点[17]，同时根据演化稳定均衡，预测博弈者的群体行为。演化博弈论已被证明是在多种场景下分析行为的可靠方法，如行人过街时与驾驶人的博弈[18]、驾驶人强行变道时与排队车辆的博弈[19]、跨境电商与跨境物流的协调演化博弈[20]等。鉴于此，本文致力于从微观层面分析双车道公路的超车行为，构建演化博弈理论模型以探索目标车辆驾驶人和超越车辆驾驶人不同策略选择的演化过程。首先基于影响博弈双方决策的因素，建立了博弈模型；其次，基于动态系统的局部稳定性原理，分析了不同策略支付关系对应的进化稳定策略（Evolutionary Stable Strategy,ESS）；最后基于实际调查数据，通过MATLAB 进行系统动力学仿真，验证了ESS的可靠性。

1 演化博弈模型构建

在双车道公路上当驾驶人遇到前方有行驶较为缓慢的车辆时，面临两种策略选择：超车与跟随。从某种程度上说超车能节省时间，其次可以得到精神上的满足。然而双车道道路较窄，强行超车会增加与前方车辆碰撞的风险。此外由于视野受限，在超车过程中驾驶人亦易与其他交通参与者发生碰撞，造成交通事故。并且如果偶尔一次强行超车没有发生风险，随着时间推移，驾驶人会经常选择执行超车策略。同样，当驾驶人在双车道公路行车过程中遇到后方有车辆试图超车时，前车驾驶人会面临加速阻止、匀速行驶和减速让行这三种策略选择，其中加速阻止会产生更大的风险，因此被视为消极应对策略；匀速行驶和减速让行是较为缓和的应对行为，在实际的道路交通场景中被视为积极应对策略。由于匀速行驶和减速让行产生的收益与损失不同，因此在本研究中，以减速让行为代表，研究驾驶人执行积极应对策略时的效应。基于上述分析，构建博弈模型G如下：

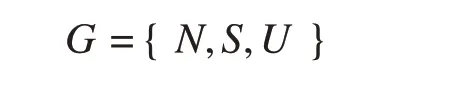
式中：N为博弈的参与人集合，即前车驾驶人和后车驾驶人；S为博弈方的策略空间，S= {S1,S2}，S1表示后车驾驶人的策略集合，S1={强行超车，跟随行驶}，S2表示前车驾驶人的策略集合，S2={积极应对，消极应对}；U为博弈方的收益与损失之和。

后车驾驶人与前车驾驶人进行博弈产生的支付矩阵如表1所示。

表1 博弈的支付矩阵Tab.1 Payoff matrix of game

表中：b1表示后车驾驶人强行超车的时间收益；b2表示后车驾驶人强行超车的精神收益；d1表示当前车驾驶人消极应对时，后车驾驶人强行超车遭受的碰撞风险；d2表示当前车驾驶人消极应对时，后车驾驶人强行超车产生的不良情绪；p1表示当后车驾驶人强行超车时，前车驾驶人采取积极应对时获得的安全收益；q1表示当后车驾驶人强行超车时，前车驾驶人采取消极应对时遭受的碰撞风险；q2表示当后车驾驶人强行超车时，前车驾驶人采取消极应对时产生的不良情绪；q3表示前车驾驶人积极应对时遭受的速度损失；b1,b2,d1,d2,p1,q1,q2,q3>0,0 ≤γi≤1(i= 1,…,8)。

2 双车道公路超车效用评价问卷设计与调查

2.1 问卷设计

由支付矩阵可知，驾驶人每种策略的收益与损失都受到多个策略效用影响变量的影响，且相对于前车驾驶人和后车驾驶人，每个策略效用影响变量的影响效果亦不相同。因此，在分析双车道公路超车行为的演化过程之前，为了获取不同角色驾驶人对每个效用影响变量的评价数值，本研究根据博弈支付矩阵设计双车道公路超车效用评价问卷，以确定不同角色驾驶人策略效用影响变量及其权重系数。

双车道公路超车效用评价问卷以Feng等人开发的驾驶人收益问卷和交通管理部门收益问卷为基础改编而来[21]，共计12 个题项。其中后车驾驶人超车收益与损失评价包括6 个题项：4 个题项用于衡量每个效用影响变量的损益程度，主要调查了驾驶人对强行超车所获得的收益情况（如：心情愉悦程度、出行时间缩短等）和强行超车遭受损失情况（如：前车驾驶人消极应对导致的碰撞风险、前车驾驶人消极应对引发的不良情绪等）；剩下2个题项用于衡量每种策略的收益，同时作为因变量，被用来确定后车驾驶人选择策略的效用影响变量的权重系数。前车驾驶人超车收益与损失评价亦包括6个题项：其中4个题项用于调查前车驾驶人对消极应对的损失（如：后车驾驶人强行超车导致的碰撞风险、后车驾驶人强行超车导致的不良情绪），以及积极应对的收益（如：降低了与后车发生碰撞的风险）和损失（如：增加了出行的时间成本）；另2个题项亦被用于衡量每种策略的收益与损失，同时作为因变量，被用来确定前车驾驶人选择策略的效用影响变量的权重系数。

由于驾驶人效用影响变量中既有关于心理的虚拟变量（如：愉悦感），亦有数值型变量（如：出行时间），变量的属性不同，各变量的度量亦不相同，因此对每个问题的回答主要衡量每个变量的收益与损失程度。为了消除属性和大小差异的影响，选项共分为5 个级别：其中，策略总效用变量用-2到2 来衡量，-2 代表损失远大于收益，2 代表收益远大于损失；效用影响变量用1 到5 来衡量，1 代表收益或损失最低，5代表收益或损失最高。

2.2 问卷调查

在正式调查之前随机选择了20名具有双车道公路驾驶经验的驾驶人，对双车道公路超车效用评价问卷进行预调查。参与者按照要求完成了问卷，并指出了其中不合理的内容，根据参与者提出的建议，对问卷进行了最终修订。由于受到新冠肺炎疫情影响，本次调查采用线上调查，依据问卷星问卷调查平台开展网上调研，并告知用户填写问卷可以获得5 元现金报酬以吸引受访者填写问卷。在填写问卷之前，用户会被问及是否有双车道公路驾驶经历，回答为“否”的用户将会自动丧失填写本次问卷的资格。此外，为了保障问卷的填写质量，本次调查设置了一些限制：首先，同一IP 地址的用户不能重复填写问卷；其次，填写时间低于30秒的问卷将被系统自动标注为无效问卷；最后，问卷中设置了1 个筛选题项（本道题请您选择非常同意）[22]。最终，本研究共获得672份有效问卷。

3 演化模型建立与分析

3.1 权重系数求解

权重系数反映了支付矩阵中各变量对博弈方的影响程度，权重系数越大，相应变量的影响越显著。支付矩阵中有8 个影响变量，相应假设了8 个权重系数。为了确定每个影响变量的权重系数，建立了四个回归模型，并用最小二乘法求解。模型1 用于确定后车驾驶人强行超车策略和跟随行驶策略的权重系数。模型2 和模型3 用于确定前车驾驶人积极应对策略和消极应对策略的权重系数。3 个模型的结果如表2 所示。此外，对标准化残差进行分析发现，所建立的模型满足残差符合正态分布的假设。

表2 决策效用影响变量权重系数及检验结果Tab.2 Results of weight coefficients solving and tests

3.2 演化模型建立与求解

设α和β分别表示后车驾驶人选择强行超车策略的比例和前车驾驶人选择消极应对策略的比例，则后车驾驶人选择跟随行驶策略的比例为1-α，前车驾驶人选择积极应对策略的比例为1-β。α和β通常是时间t的函数。则采用强行超车策略和消极应对策略的后车驾驶人的期望收益与损失之和U11、U12以及后车驾驶人群体的平均期望收益与损失之和——U1，分别为：

采用消极应对策略和积极应对策略的前车驾驶人的期望收益与损失之和U21、U22以及前车驾驶人群体的平均期望收益与损失之和——U2，分别为：

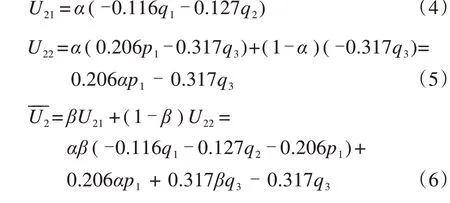
演化博弈论认为，个体在现实中并不总是执行最优决策，个体决策是在动态过程中做出的，例如模仿、学习和变异等。在本模型中，后车驾驶人和前车驾驶人都有基本的经验判断能力，经过一段时间的演化，博弈双方会发现不同策略带来的收益差异，收益差的一方会改变策略。这表明博弈双方选择某种策略的比例α和β是随着时间动态变化的。复制动态方程是描述某一特定策略在一个种群中被采用的频数或频度的动态微分方程，被用于研究博弈双方的策略调整过程。后车驾驶人群体中选择强行超车策略和前车驾驶人中选择消极应对策略的复制动力学方程如下[23]：

3.3 演化稳定策略分析

在双车道公路的超车过程中，前车驾驶人和后车驾驶人之间的博弈是一个长期的过程，在此过程中，双方都通过学习积累决策经验，并动态调整策略，以尽可能提高自身收益。探索前车驾驶人群体和后车驾驶人群体的博弈过程，一个关键目标就是寻找ESS。ESS 是一种策略组合，当这种策略组合被博弈双方采用时，这种策略不会被其他小群体采用的其他策略所改变[24]。

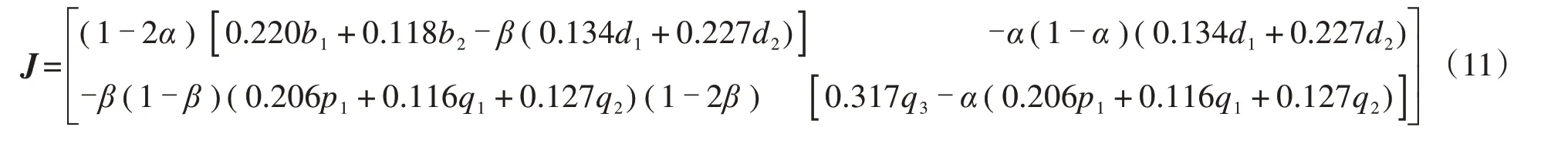
雅克比矩阵J的行列式和迹的值被用来判断平衡点的稳定性，同时亦被用来确定前车驾驶人和后车驾驶人之间博弈的演化稳定策略。表3 展示了局部均衡解对应雅克比矩阵J的行列式和迹。由于不同的策略支付关系会影响博弈双方的策略选择，本研究讨论了4种策略支付关系下双方的博弈过程和演化稳定策略。为后面便于描述，记

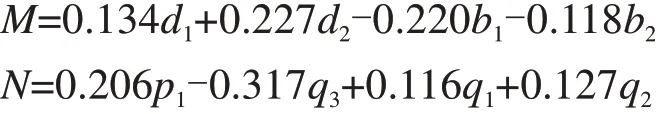
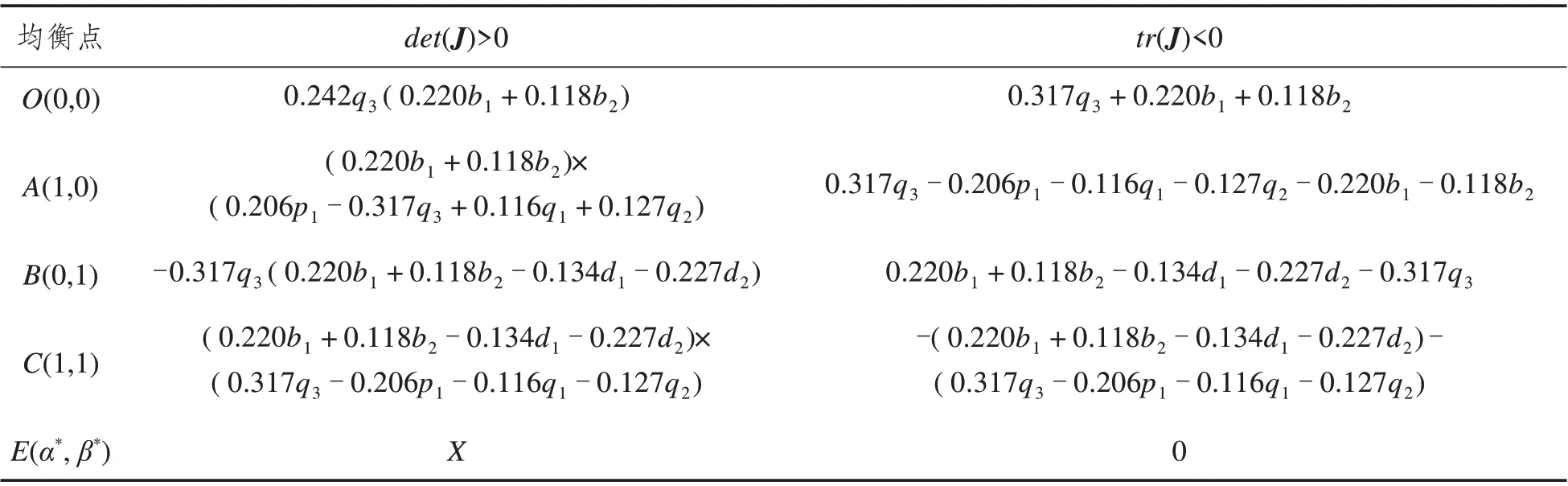
表3 局部均衡解对应的det(J)和tr(J)Tab.3 Det(J)and tr(J)corresponding to partial equilibrium solution

（1）M<0,N>0

此种情况是不管前车选择消极应对或积极应对，后车选择强行超车获得的收益与损失之和均高于跟随行驶获得的收益与损失之和，同时当后车强行超车时，前车选择积极应对时获得的收益与损失之和更高。如表4 所示，此时系统有4 个平衡点：O(0,0)，A(1,0)，B(0,1)和C(1,1)。由雅克比矩阵的局部稳定性原理可得，该情形下局部均衡点中A(1,0)具有稳定性，是后车驾驶人与前车驾驶人博弈的演化稳定策略；B(0,1)和C(1,1)是鞍点，O(0,0)是不稳定点。图1 体现了博弈的动态演化过程，表明无论博弈双方从任意状态开始博弈，最终后车驾驶人均会选择超车策略，前车驾驶人均会选择积极应对策略。

表4 策略支付关系1的均衡点Tab.4 Classification of equilibrium points for strategy payoff relationship 1

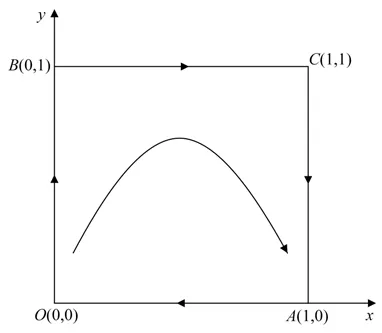
图1 系统演化相位图（策略支付关系1）Fig.1 System evolution phase diagram(strategy payoff relationship 1)

（2）M<0,N<0

此种情况是不管前车选择消极应对或积极应对，后车选择强行超车的收益与损失之和均高于跟随行驶获得的收益与损失之和，同时当后车强行超车时，前车选择消极应对获得的收益与损失之和更高。如表5 所示，此时系统有4 个平衡点：O(0,0)，A(1,0)，B(0,1)和C(1,1)。由雅克比矩阵的局部稳定性原理可得，该情形下局部均衡点中C(1,1)具有稳定性，是后车驾驶人与前车驾驶人博弈的演化稳定策略；A(1,0)和B(0,1)是鞍点，O(0,0)是不稳定点。图2体现了博弈的动态演化过程，表明无论博弈双方从任意状态开始博弈，最终后车驾驶人均会选择强行超车策略，前车驾驶人均会选择消极应对策略。

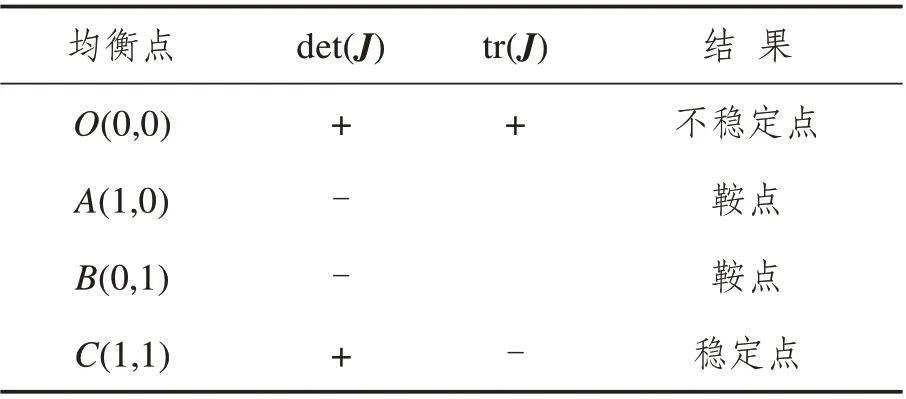
表5 策略支付关系2的均衡点Tab.5 Classification of equilibrium points for strategy payoff relationship 2

图2 系统演化相位图（策略支付关系2）Fig.2 System evolution phase diagram(strategy payoff relationship 2)

（3）M>0,N>0

此种情况是当前车选择消极应对时，后车选择跟随行驶获得的收益与损失之和更高，同时当后车强行超车时，前车选择积极应对获得的收益与损失之和更高。如表6 所示，此时系统有5 个平衡点：O(0,0)，A(1,0)，B(0,1)，C(1,1)和E(α*,β*)。由雅克比矩阵的局部稳定性原理可得，该情形下局部均衡点中A(1,0)和B(0,1)具有稳定性，是后车驾驶人与前车驾驶人博弈的演化稳定策略；E(α*,β*)是鞍点，O(0,0)和C(1,1)是不稳定点。图3 体现了博弈的动态演化过程，这表明，前车驾驶人与后车驾驶人出现配合（前车消极应对和后车跟随行驶，后车强行超车和前车积极应对）的收益与损失之和，比其他策略组合的收益与损失之和更大。此时，博弈系统趋于稳定。

表6 策略支付关系3的均衡点Tab.6 Classification of equilibrium points for strategy payoff relationship 3

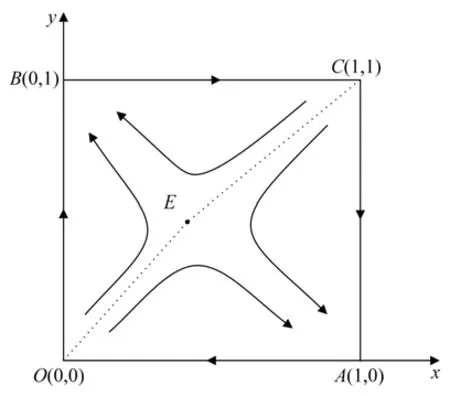
图3 系统演化相位图（策略支付关系3）Fig.3 System evolution phase diagram(strategy payoff relationship 3)

（4）M>0,N<0

此种情况是当前车选择消极应对时，后车选择跟随行驶获得的收益与损失之和更高，同时当后车强行超车时，前车选择消极应对获得的收益与损失之和更高。如表7 所示，此时系统有4 个平衡点：O(0,0)，A(1,0)，B(0,1)和C(1,1)。由雅克比矩阵的局部稳定性原理可得，该情形下局部均衡点中B(0,1)具有稳定性，是后车驾驶人与前车驾驶人博弈的演化稳定策略；A(1,0)和C(1,1)是鞍点，O(0,0)是不稳定点。图4 体现了博弈的动态演化过程，这表明无论博弈双方从任意状态开始博弈，最终后车驾驶人均会选择跟随行驶策略，前车驾驶人均会选择消极应对策略。

图4 系统演化相位图（策略支付关系4）Fig.4 System evolution phase diagram (strategy payoff relationship 4)

表7 策略支付关系4的均衡点Tab.7 Classification of equilibrium points for strategy payoff relationship 4

4 演化博弈模型的模拟仿真

4.1 模拟数据

演化稳定策略分析中未使用效用影响变量的权重系数。根据策略支付关系，将前车组和后车组各分为两组。

后车组1满足：

通过将2 组前车组和2 组后车组相结合，创建了4 个案例研究，每个案例研究代表1 种支付策略关系。将属于同一组的每个问题的平均回答值作为相应案例研究的效用影响变量的数值。表8 展示了4组驾驶人的效用影响变量的数值。

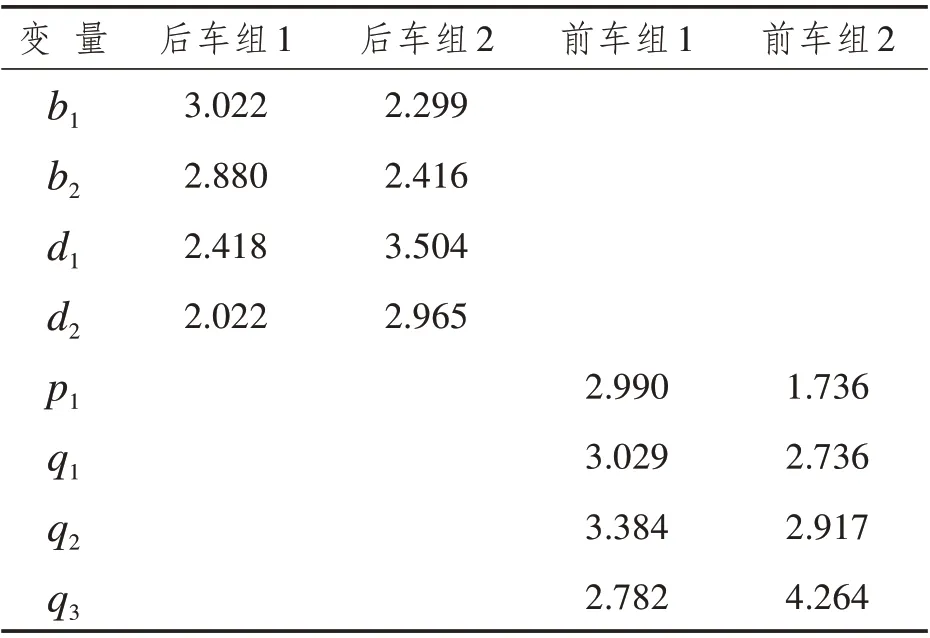
表8 驾驶人效用影响变量的数值Tab.8 Numerical values of drivers’payoff influence variables

4.2 模拟结果

为了形象地演示前车驾驶人与后车驾驶人的策略选择进化过程，本节使用MATLAB 9.1.0 进行模拟仿真，模拟周期设置为40，时间步长设置为0.5。基于支付矩阵和复制动态方程构建仿真模型，绘制不同策略支付关系的演化曲线。 4 种策略支付关系的相关参数的初始值如表8所示。

4.2.1 案例1

前车驾驶人与后车驾驶人采取消极应对策略和强行超车策略的初始概率分别取（0.2,0.8）和（0.2,0.2）。随着演化时间推移，可以获得如图5 所示的演化轨迹。可以发现，前车驾驶人和后车驾驶人的演化博弈结果与前文推导的演化稳定策略是一致的。在此种情况下，超车演化博弈的稳定策略不受初始状态的影响。随着后车驾驶人采取强行超车策略概率的升高，前车驾驶人采取消极应对策略的概率先升高后降低。此外，无论是哪种初始概率，后车驾驶人的演化曲线收敛于均衡点的速度都更快。最终，后车驾驶人会选择强行超车策略，而前车驾驶人会选择积极应对策略，双方形成一种较为安全的超车模式。交通管理部门在进行安全教育时，应结合具体案例，引导驾驶人在面对被超车的情形下保持礼让的行车观念，在条件允许的情况下，降低速度，靠右行驶，减少并排行驶的时间，避免争快斗狠。

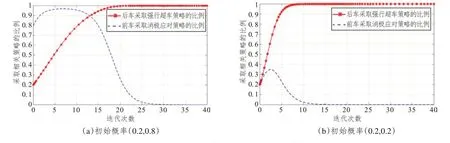
图5 不同初始状态下策略选择的进化过程（案例1）Fig.5 Evolutionary process of strategy selection for different initial states(case 1)

4.2.2 案例2

前车驾驶人与后车驾驶人采取消极应对策略和强行超车策略的初始概率分别取（0.2,0.2）和（0.8,0.8）。随着演化时间推移，可以得到如图6 所示的演化图。可以发现仿真得到的前车驾驶人和后车驾驶人的演化博弈结果与上文推导的演化稳定策略一致。在此种条件下，博弈双方演化博弈的稳定策略不受初始状态的影响。最终，后车驾驶人会选择强行超车策略，而前车驾驶人会选择消极应对策略。进一步观察可得，无论是哪种初始概率，后车驾驶人的演化曲线收敛于均衡点的速度都比前车驾驶人更慢，这表明前车驾驶人会更快地选择消极应对策略。在此种情形下，前车驾驶人消极应对，后车驾驶人试图强行超车，双方驾驶人互不相让，车速较快且易出现并排行驶，超车过程极为危险。交通管理部门应强调强行超车造成的危害，教育引导驾驶人在行车环境复杂的道路上减少超车，同时要注意礼让，以避免这种“针锋相对”的局面。

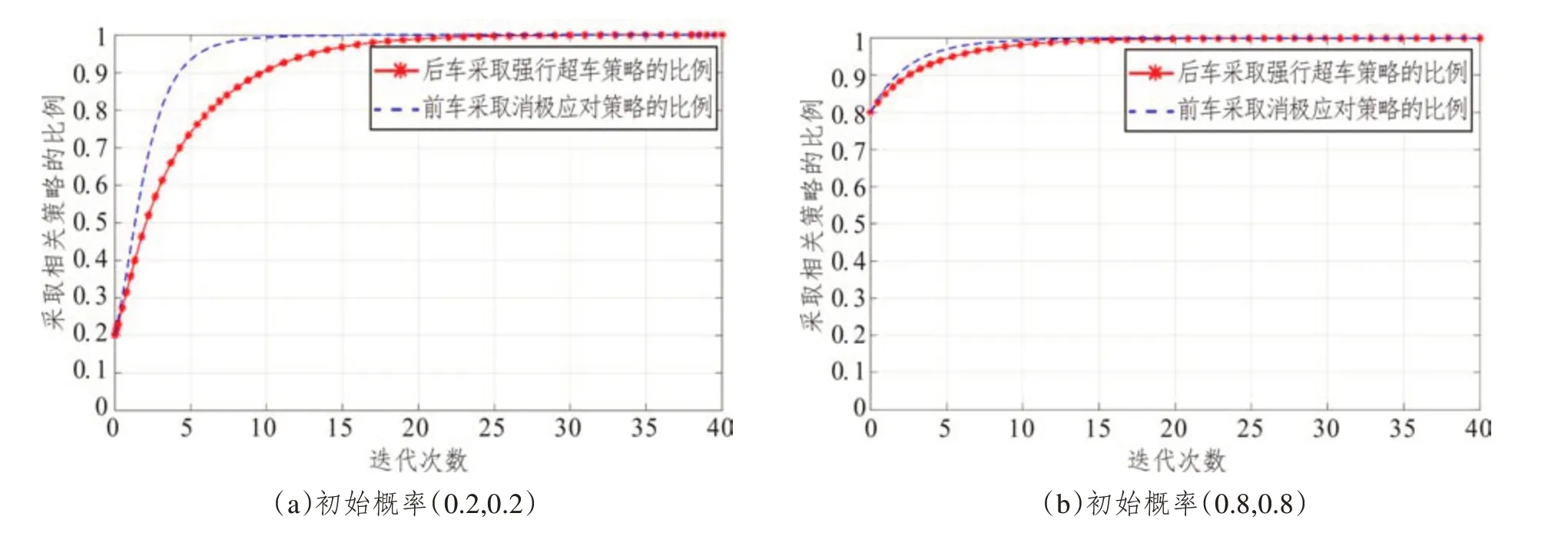
图6 不同初始状态下策略选择的进化过程（案例2）Fig.6 Evolutionary process of strategy selection for different initial states(case 2)

4.2.3 案例3

前车驾驶人与后车驾驶人采取消极应对策略和强行超车策略的初始概率分别取（0.2,0.2）、（0.2,0.8）、（0.8,0.2）和（0.8,0.8）。随着演化时间的推移，可以获得如图7所示的演化轨迹。可以发现仿真得到的前车驾驶人和后车驾驶人的演化博弈结果与上文推导的演化稳定策略一致。在此条件下，参与者演化博弈的稳定策略受初始状态的影响。如图7所示，当初始概率取（0.2,0.2）、（0.8,0.2）和（0.8,0.8）时，最终后车驾驶人会采取强行超车策略，前车驾驶人会采取积极应对策略。此外，进一步观察可知，在三种概率条件下，后车驾驶人的演化曲线收敛于均衡点的速度都比前车驾驶人快，表明后车驾驶人会更快地选择强行超车策略。另一方面，当初始概率取（0.2,0.8）时，最终前车驾驶人会采取消极应对策略，后车驾驶人会采取跟随行驶策略。此种情况下，前车驾驶人的演化曲线收敛于均衡点的速度比后车驾驶人快，前车驾驶人会更快地选择消极应对策略。当驾驶人在双车道公路上的超车较低时，前车驾驶人的不让行会降低后车驾驶人强行超车的概率，因此交通管理部门可以倡导驾驶人在双车道公路上不进行超车，降低超车的初始概率，进而避免强行超车的发生。

图7 不同初始状态下策略选择的进化过程（案例3）Fig.7 Evolutionary process of strategy selection for different initial states(case 3)

4.2.4 案例4

前车驾驶人与后车驾驶人采取消极应对策略和强行超车策略的初始概率分别取（0.2,0.2）和（0.8,0.2）。随着演化时间的推移，可以获得如图8所示的演化轨迹。可以发现仿真得到的前车驾驶人和后车驾驶人的演化博弈结果与上文推导的演化稳定策略一致。该情形下，前车驾驶人和后车驾驶人演化博弈的稳定策略不受初始状态的影响。最终，前车驾驶人会采取消极应对策略，后车驾驶人会采取跟随行驶策略。进一步观察可得，随着时间推移，前车驾驶人采取消极应对策略的概率不断提升，后车驾驶人采取消极应对策略的概率先升高后降低；后车驾驶人的演化曲线收敛于均衡点的速度都比前车驾驶人快，表明后车驾驶人会更快地选择强行超车策略。

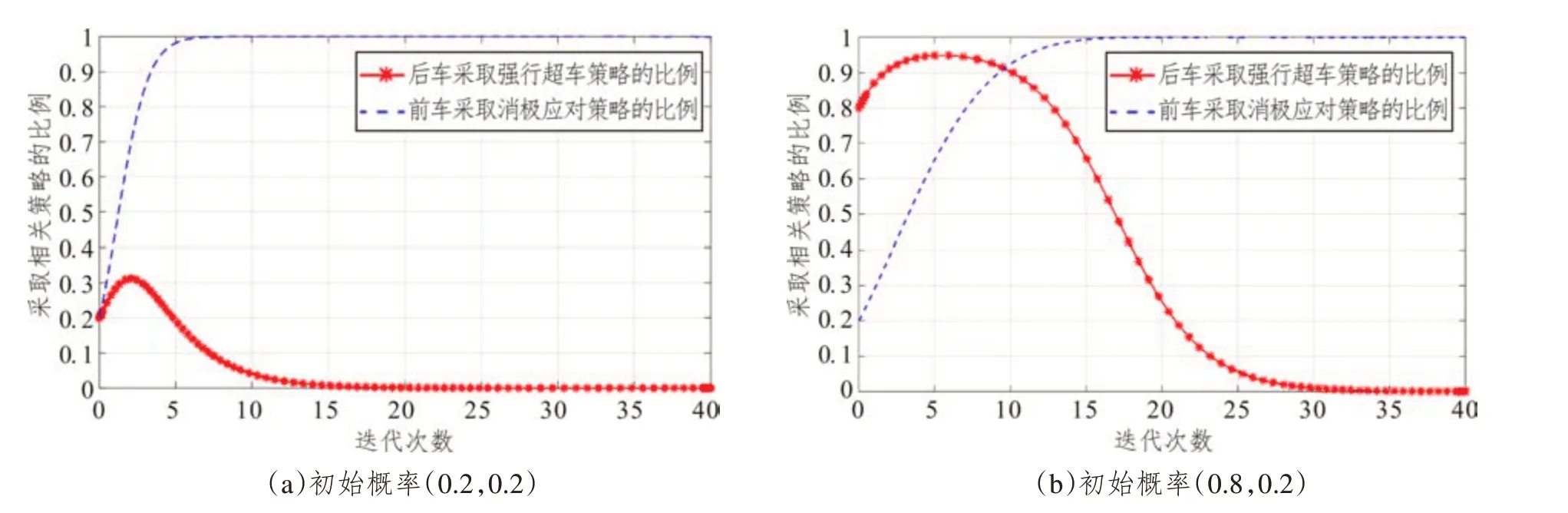
图8 不同初始状态下策略选择的进化过程（案例4）Fig.8 Evolutionary process of strategy selection for different initial states(case 4)

5 结束语

本文基于演化博弈理论对双车道公路超车驾驶行为展开了研究，以实际调查数据为基础，建立了演化模型，验证了该模型对解释超车驾驶行为的有效性。通过实际调查的数据对演化博弈过程中的复制动态方程进行了仿真，揭示了博弈双方在发展过程中采用各种策略的演化特征，主要研究结论如下：

（1）基于演化博弈分析可知，通过针对不同类型驾驶人进行有效的交通安全教育，可缩短博弈系统的演化时间，以便更快速地达到安全稳定的均衡状态。

（2）在大部分情境下，前车驾驶人与后车驾驶人最终均会达到后车选择强行超车和前车选择积极应对，或前车选择消极应对和后车选择减速跟随的安全均衡状态。

（3）对于满足M>0,N>0 的驾驶人，若前、后车驾驶人选择消极应对和强行超车的比例同时较低，反而会增加博弈演化时间，系统需要更长的时间才能到达均衡状态，超车过程中存在着较大概率并排行驶的可能性。因此交警部门在进行安全宣传教育时，应做好对超车行为的指导，驾驶人超车时应果断、安全快速通过。

（4）对于满足M<0,N<0 的驾驶人，前、后车驾驶人互不相让，此时极为危险。交警部门应从政策上和物质上加大对此类驾驶人不当超车的处罚，加强对此类驾驶人的教育。同时，教育前车驾驶人在条件允许时，应减速行驶，靠右让行，切忌冲动驾驶。

相较于其他研究，本文中所采用的各效用影响变量的权重系数来自于实际调查数据，构建的模型更加客观。但本文所构建的模型具有一定的局限性，驾驶人在决定是否进行超车时可能存在多次博弈的情况，因此还需考虑博弈双方在超车过程中的学习与认知，建立深层次的认知博弈模型。