环线对地铁网络弹性的影响研究

潘守政，何 佳，王英平，贺正冰

（1.北京工业大学，交通工程北京市重点实验室，北京 100124；2.交通运输部规划研究院，北京 100028）

0 引 言

在地铁网络受干扰而中断的分析中，级联失效是一个重要的研究方向，很多国内外学者对此进行了研究。黄爱玲等[3]建立了加权网络下的耦合映像格子模型，对网络的有权和无权要素进行耦合，研究了P 空间下地铁网络的级联失效行为。修志博[4]分析了不同重要度的节点失效时产生的级联失效反应，并对耦合系数进行了设定。熊志华等[5]使用级联失效模型对轨道交通网络上客流的拥堵传播效应进行了分析，对初始值的选取和耦合参数进行了多种场景下的仿真分析。朱岩等[6]研究了上海地铁网络在面对级联失效时的可靠性变化，发现强度越大的节点故障传播能力越强，而耦合因子越大级联失效的速度也越快。然而目前的级联失效实验都是以节点为基本单元，没有区分不同类型站点失效所带来的影响，而不同鲁棒类型的站点面对级联失效的反应（如失效阈值的不同）是不同的，现有的耦合映像格子模型还无法区分。

Sun 和Guan[7]没有以传统的节点或连边作为失效对象，而是从线路运营的角度分析了城市地铁网络的脆弱性。通过收集运营线路的客流量数据，又结合传统的全有全无分配法，在拓扑结构分析的基础上得出了不同中断概率下的脆弱线路。作者发现客流是引起网络脆弱性的关键因素，而环形线路在运营中具有更强的鲁棒性[8]，且线路的中断不是孤立的，必然要影响相关的站点和线路。因此本文将改进的级联失效模型分别应用于站点和线路水平，将不同站点和线路的状态变化联系起来，尤其对环线结构的脆弱性和鲁棒性进行了深入分析。

对于网络恢复阶段的研究目前还较少，尤其是基于复杂网络理论的分析，大部分学者都是以弹性指数的形式对网络恢复性能进行衡量。Brunneau[9]在2003年提出弹性三角形概念，将弹性具体计算过程聚焦于弹性分析模型中的恢复过程。类似地，Twumasi-Boakye[10]等也用面积来表征弹性，但是更关注从失效到恢复整个过程的变化，而将网络失效阶段与恢复阶段的分析结合可以使网络性能的评价更加完整和客观。

环形线网简称环线，是城市轨道交通网络中一种首末站点重合的闭环线路，具有特殊的拓扑特性和运营功能。在很多城市的城轨网络（如我国的北京地铁、上海地铁、成都地铁等，以及莫斯科地铁、东京地铁等）都拥有环绕城市中心建设的地铁线路。它们的地理布局特殊，往往同时与很多其他线路相连，有着重要的拓扑意义；同时，它们普遍还承接着较大的客流需求和换乘现象。因此不论是从复杂网络角度来看，还是从运营角度来看，环线都是整个网络中比较重要的线路结构。现有研究也表明了环线的特殊性和重要性[7-8]，因此更具针对性地研究环线受到干扰后对整个城市轨道交通网络性能的影响很有必要。

环线在地铁网络中是一种特殊的拓扑结构，它既起到了串联不同线路的作用，使网络的连通性和可达性大大提高[11]，又使得网络联系更加紧密，但如果某一节点受到干扰也可以很快传播到其他节点甚至整个网络性能都会受到影响。Sun和Guan[7]发现上海地铁中的4 号环线具有最高的平均介数值，而在客流加权的地铁网络中，环线和连接中心及郊区的径线都很重要[8]。目前，国内外针对地铁环线对网络性能影响尤其是弹性方面的研究还较少，对于级联失效下的环线作用机理了解仍然不多。与图论中单纯的拓扑结构不同[12]，交通系统中重要的客流因素赋予了地铁网络不同元素间更加复杂的联系，而客流加权下的环线结构对网络弹性的影响还没有被深入探究。因此，研究地铁环线的级联失效对整个客流加权网络的性能影响具有重要意义，也可以促进复杂网络理论的发展。本文以北京市地铁为例，从网络弹性的角度出发，基于图论和改进的耦合映像格子模型深入分析环线结构在网络失效和恢复过程中的影响作用。研究结果为目前具有环线结构的地铁系统的日常运营和维护提供了参考，预防和降低因系统故障而引发网络瘫痪的风险，也为新建地铁的线网规划提供重要的理论依据。

1 网络弹性分析和评价方法

1.1 基于耦合映像格子的级联失效模型

耦合映像格子模型是研究混沌系统的常用工具，它将系统的时间和空间属性离散化，但可以对系统的状态变化进行连续性的动力学分析[4]。将该模型应用于网络的级联失效行为分析可以有效探究不同站点和线路间的耦合效应对网络相继故障行为的影响[5]。在实际中，不同站点和线路的鲁棒性存在差异，受到不同程度的干扰后的失效阈值也应有所不同，因此本文在黄爱玲等[3]提出的模型基础上，建立了针对不同站点鲁棒性差异下的异质状态更新模型，即采取拓扑结构和客流两种因素耦合，针对不同类型站点探究二者共同影响下环形线网的级联失效反应。考虑到拓扑结构耦合系数对传播过程、故障峰值的影响较小，而流量分布耦合系数在考虑出行行为选择的情况下也影响较小[3]，且蓄意攻击模式下，故障传播特性受R值影响较小，因此选择固定的耦合系数进行研究。设ξ定拓扑结构耦合系数ξ1为0.25，流量耦合系数ξ2为0.25，ξ1,ξ2∈(0,1)且ξ1+ξ2<1。

本文中aij表示节点间的连接状态，当节点i和j之间有连边时为1，否则为0；d(i)为节点i的度值；s(i)为节点i的强度值（即客流加权下的度值）；K为初始干扰值且K≥1[3]。对于不同站点鲁棒性差异下的异质状态更新过程：节点i在t+1 时刻的状态xi(t+1)由上一时刻的该节点状态、鲁棒性或脆弱性值ΔCi以及相邻节点的状态决定。当状态值超过指定阈值Ti时判定该节点失效，在之后的状态都固定为0。下一时刻失效节点的周边节点的状态值将受到影响并可能产生状态值大于对应节点阈值的节点，从而继续判定失效。随着时间推移网络便自动产生了级联失效反应，直至所有节点的状态值都小于Ti或等于0。f(x)为非线性映射函数，表示站点i的容量演化规律。本文采用一维映射函数f(x)=ax(1-x)，1 ≤a≤4，通常取a= 4。在网络初始阶段，任意节点的状态值在0-1范围内随机给出。初始干扰模型为：

他跟着那个挣扎前进的人的痕迹向前走去，不久就走到了尽头——潮湿的苔藓上摊着几根才啃光的骨头，附近还有许多狼的脚印他发现了一个跟他自己的那个一模一样的厚实的鹿皮口袋，但已经给尖利的牙齿咬破了。他那无力的手已经拿不动这样沉重的袋子了，可是他到底把它提起来了。比尔至死都带着它。哈哈！他可以嘲笑比尔了。

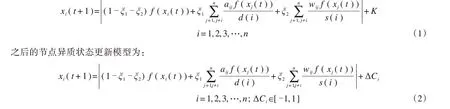
假定常规站点的基础阈值为1，ΔCi=1-Ti。当节点的阈值大于1（鲁棒性站点），ΔCi<0；节点的阈值小于1（脆弱性站点），ΔCi>0；而当节点为常规站点，失效阈值为1，ΔCi= 0。

1.1.1 客流重分配规则

在地铁网络中，当某一站点失效，其相邻连边上的客流会就近涌入周边节点，引起周边客流的重分布，如图1所示。

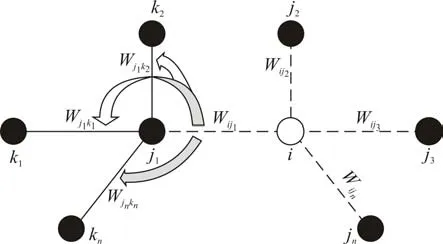
图1 节点失效下的网络客流重分配示意图Fig.1 Diagram of network flow redistribution under a node failure

因此，在级联失效模型下，可定义如下客流重分配的原则[3]。当站点i失效后，与之直接相邻的连边ijn也随之失效，连边的流量Wijn将被重新分配到周边节点j1,…,jn各自相邻的连边Wjnkn中，如图1中箭头所示为其中一条连边Wij1失效后的客流重分配。分配之后这些相邻连边的客流权重Wjnkn将发生变化，如公式（3）所示。新的客流权重W new j1kn为原有客流权重Wjnkn和新分入客流ΔWj1kn之和。新分入客流ΔWj1kn的比例依据原有客流Wjnkn占节点相邻连边的总客流Sjn比重得到：

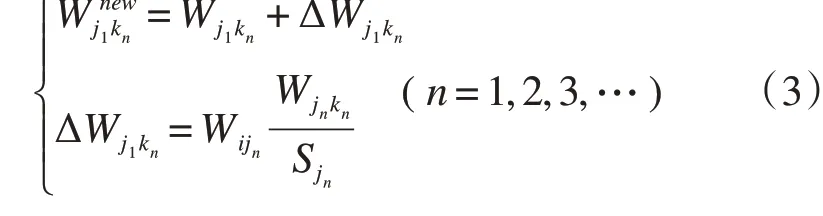
1.2 基于弹性分析模型的环线作用评价

地铁系统弹性是一个动态变化的过程[1]，即面对系统内部（如信号短暂中断）和外部（如突发大客流）的各种干扰，系统大多数情况下都能自我调整从而维持在正常性能水平。当面对一个突发的严重干扰时（如暴雨内涝、火灾等），系统性能会大大降低，甚至瘫痪。这时需要外界救援和进行自我修复，经过一段时间才能恢复到正常水平，具体变化过程如图2 所示[2]。基于复杂网络理论，将地铁系统抽象为网络拓扑结构，更有利于系统的性能分析。本文将地铁站点抽象为网络节点，分为换乘站和非换乘站点。不同站点之间的连接路段抽象为网络的连边。由于同一地铁线路的上下行路径基本一致，遇到突发事件时往往双向关闭，因此将地铁网络抽象为无向加权网络，在此基础上进行地铁网络弹性的分析。而客流因素也是地铁网络中的重要组成部分[13]，因此利用真实客流数据对网络加权，根据网络弹性的变化过程，分两个阶段对网络弹性进行定量分析。在中断过程中采用运营效率（见公式5）和节点失效比例作为弹性评价指标。

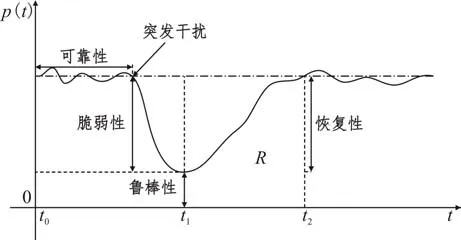
图2 地铁系统中的弹性变化Fig.2 Resilience changes in a subway system

在系统性能恢复的阶段，依据Bocchini[14]和Wang[15]提出的弹性三角形概念进行定量评估。整个网络在t1-t2时段内，通过采取一定措施使得网络性能p(t)逐渐恢复，在这个过程中，p(t)上升曲线包围的面积即为网络的弹性R。p(t)是衡量网络所能维持的正常功能水平的能力，定性来讲可以分为弹性、脆弱性、鲁棒性、可靠性等；定量来讲可以采用多种评价指标来衡量，如运营效率[16]，其定量化计算公式为：

因此在弹性恢复阶段，采用弹性指数R和运营效率μ（即客流加权下的网络效率）作为弹性评价指标：

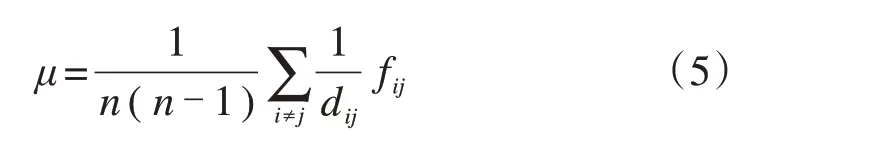
式中：dij为节点i和j之间的最短路径长度（本文采用实际的站间运行时间作为节点间距离）；fij为两站点间的实际客流量。

1.3 面向站点的中断-恢复策略

为了更好地研究地铁中环线结构对整个网络弹性性能的影响，分别从站点和线路两个角度考虑环线结构受到外界干扰失效后的地铁网络性能从降低到恢复的过程，具体策略如表1所示。首先模拟地铁站点失效后产生级联失效现象，初始节点分别选择随机节点、度值最大的节点和介数最大节点。节点度为与该节点直接相连的连边数，可以反映节点作为枢纽的重要性水平。节点介数为通过该节点的最短路径数占全网最短路径数的比值，可以反映该节点作为桥梁节点的重要性水平[4]。之后为了探究环线结构的影响，在仿真恢复阶段分别按度值大小对失效节点降序恢复，顺序分为环线和非环线上的站点；在按介数大小对失效节点降序恢复时，顺序同样分为环线和非环线上的站点。

表1 面向站点和线路的中断-恢复顺序Tab.1 Disruption-recovery sequence for stations and lines

此外，考虑到地铁网络中换乘站具有特殊的拓扑和客流特性，环线和非环线上的换乘站失效对网络弹性的影响可能也是不同的。因此，本文对现有级联失效模型进行了改进，通过设置不同位置换乘站降低和提高状态阈值来体现站点的鲁棒性高低，可以有效研究环线和非环线上的换乘站易失效和施加保护后的四种情况下的网络性能变化情况。在恢复阶段，以换乘站为单位，对比优先恢复环线或非环线的网络弹性值的变化，可以得到环线站点对整个网络恢复性能的影响。

1.4 面向线路的中断-恢复策略

在实际中，地铁网络在受到干扰时往往不是单一站点发生故障，而是多个连续区段的失效甚至整条线路失效。因此，本文还从线路的角度对环线的作用进一步分析，对比环线和径线在失效情况下的网络弹性变化。在性能降低阶段，基于改进的级联失效模型，分别研究环线易失效和施加保护两种情况下的网络性能变化。在网络性能恢复阶段，同样设置不同的恢复顺序（优先环线或非环线）来对比其作用。

2 实证分析——以北京市地铁为例

北京市地铁具有两条明显的环形线路（见图3），是作为环线对网络弹性影响的理想研究对象。同时使用2017 年10 月某周一上午早高峰6 点～8点的地铁刷卡数据。经过数据清洗得到整个地铁网络的OD 客流，采用全由全无分配法进行流量分配，从而建立地铁客流加权网络。基于第二节的弹性分析方法，从拓扑结构和客流因素角度分析环线在北京地铁网络弹性中的影响作用。

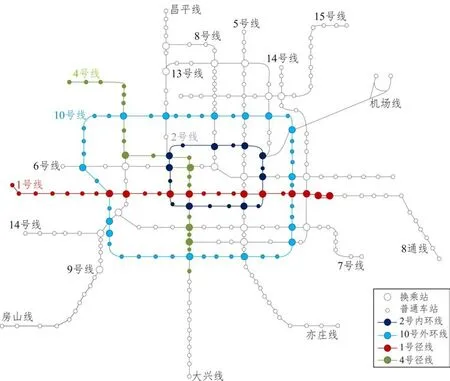
图3 北京地铁拓扑结构图Fig.3 Topological graph of the Beijing subway

2.1 面向站点的中断-恢复场景研究

分别以随机节点、度较大节点——车公庄站（排名第三）、介数较大节点——知春路站（排名第三）作为级联失效的初始攻击节点，仿真实验的结果如图4所示。由于节点的初始状态为随机给定，一组状态值产生的结果具有偶然性，因此进行了100 组重复实验，图中阴影区域为标准差覆盖区域，线条为相应均值。依据均值的变化水平，介数排名下的级联失效高峰最早出现并且失效比例最高。而基于度攻击的级联失效却最早导致网络瘫痪，运营效率的下降也最快。相比之下，随机攻击下节点的失效速度最慢，但阴影区域的波动较小，曲线变化平滑。这表明一些重要节点在网络失效过程中具有很大影响，一旦受到干扰后失效引发的级联失效反应更剧烈，且具有很大不确定性。

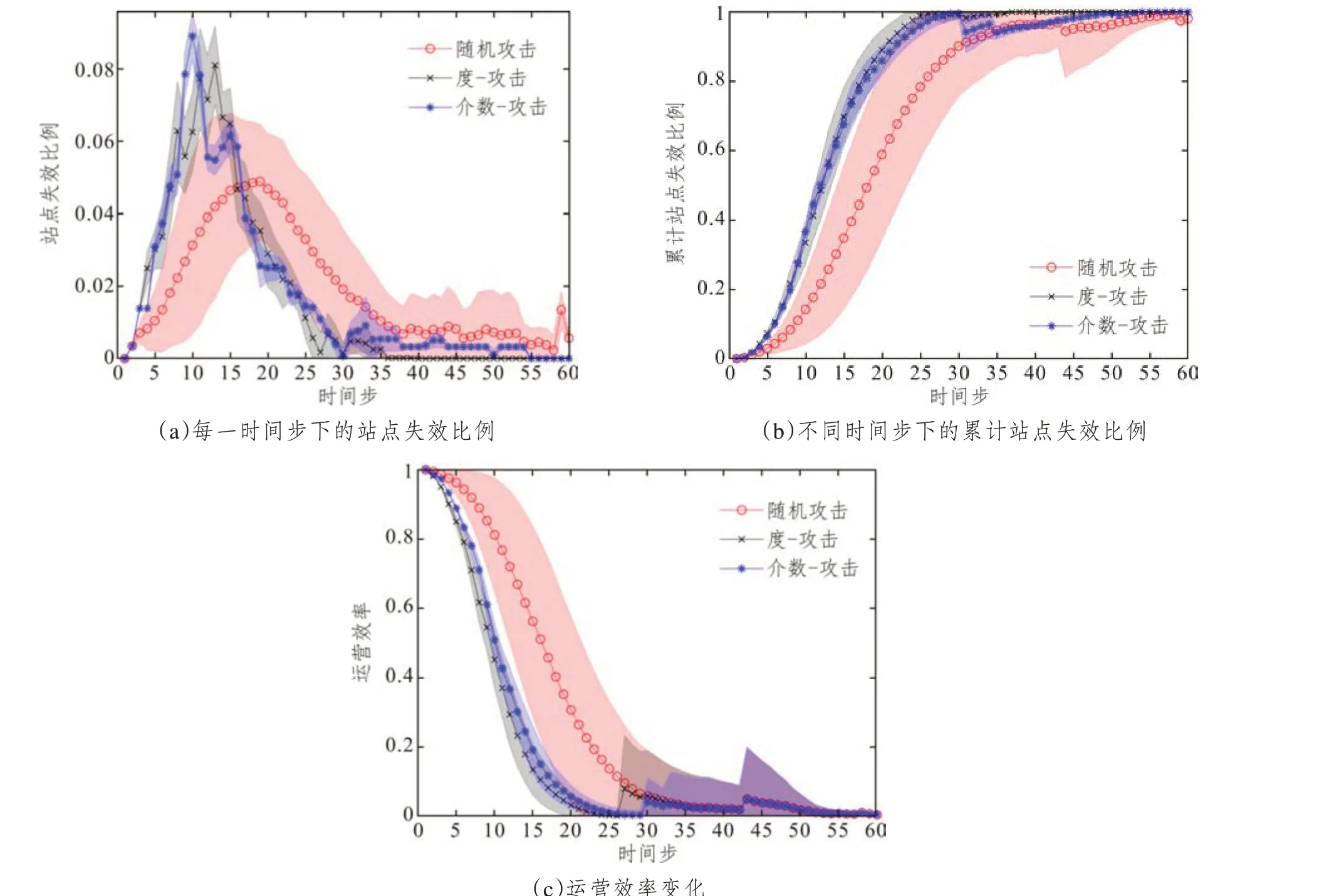
图4 不同站点攻击策略下的网络弹性变化（阴影区域为标准差）Fig.4 Network resilience changes under different attack strategies of stations

在网络失效到0%和10%时，分别采用按度值（先环线或非环线）和介数（先环线或非环线）从高到低的顺序，对网络的恢复性能进行探究。顺序一先按度值降序恢复所有环线上的站点，再恢复所有非环线上的站点。顺序二则按度值降序优先恢复所有非环线上的站点。实验结果如图5所示，在网络失效到0%时恢复，顺序一弹性为0.71，顺序二弹性为0.67。在网络失效到10%时恢复，顺序一弹性为0.73，顺序二弹性为0.70。在同一失效规模下，初始阶段两种恢复顺序下的运营效率恢复基本一致，但在中间阶段环线优先下的恢复较快。在网络失效到一定比例时，优先恢复环线使得网络具有更好的弹性恢复性能，并且较早地采取恢复措施可以更好地提高网络弹性，保障地铁系统的运营性能始终维持在正常水平。

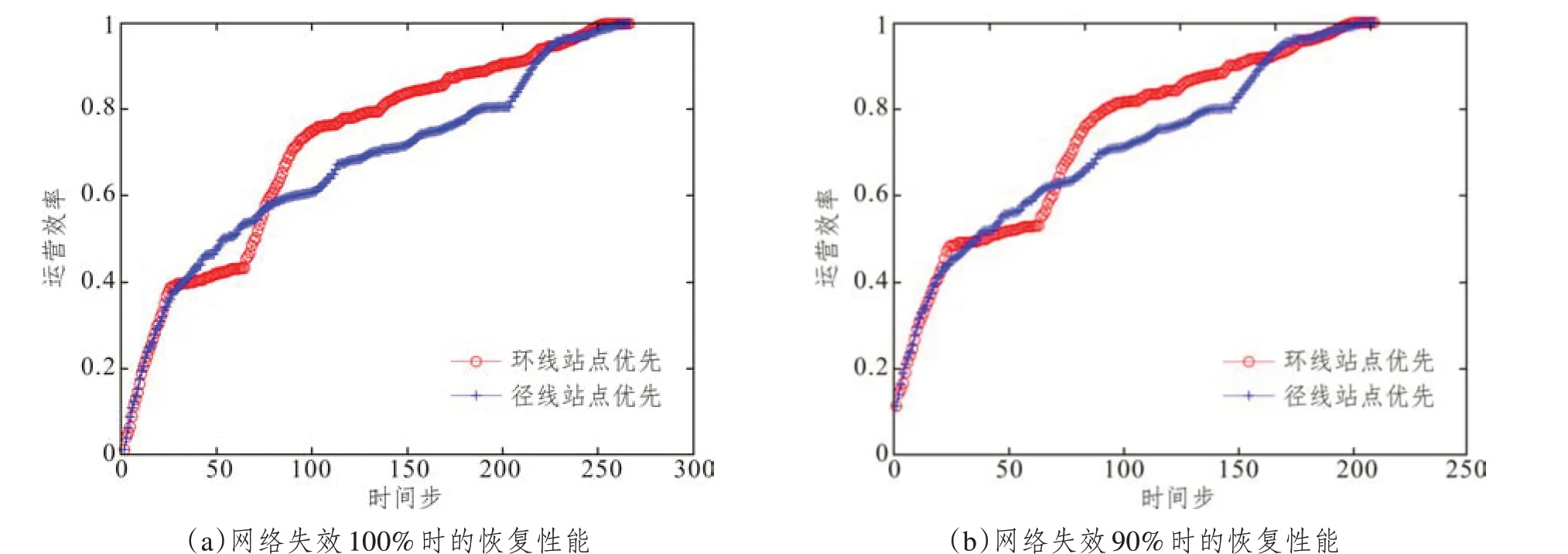
图5 基于节点度降序恢复的网络弹性变化Fig.5 Network resilience changes based on a descending recovery of the node degree

顺序三按点介数大小先恢复所有环线上的站点，再恢复所有非环线站点。顺序四按点介数大小先恢复非环线上的站点，再恢复所有环线站点。结果如图6所示，按点介数大小恢复与按度恢复效果类似。依据公式（4）可知，在网络失效到0%时恢复，顺序三弹性为0.71，顺序四弹性为0.66。在网络失效到10%时恢复，顺序三弹性为0.73，顺序四弹性为0.69。但相同的现象仍是优先恢复环线使得网络具有更好的恢复性能。

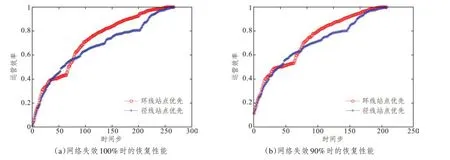
图6 基于点介数降序恢复的网络弹性变化Fig.6 Network resilience changes based on a descending recovery of the node betweenness

2.2 面向换乘站的级联失效分析

地铁网络中，换乘站是一种特殊且重要的站点，尤其是环线上换乘站点的作用值得关注。在北京市地铁网络中，环线上换乘站有25个，非环线上有26个。在级联失效阶段针对换乘站设置了两种中断方式和两种应对机制（见表1），共四种场景进行仿真分析。为体现两种应对机制下的网络弹性变化，对原耦合映像格子模型进行改进，可以针对特定类型的站点降低或提高级联失效的阈值（参数ΔCi增加或减少0.5），来突出易失效站点（脆弱型）和施加保护的站点（鲁棒型）。前两种场景下，先攻击环线度值排名第三的换乘站——车公庄站，将环线换乘站的失效阈值降低0.5（即增大换乘站脆弱性），ΔC=0.5。同理对非环线中度值排名第三的换乘站——东单站进行分析，结果如图7的（a）、（c）、（e）所示。可以看出，两种类型线路几乎同时达到失效高峰，但非环线下的失效速度和运营效率下降得更快，而环线换乘站的失效则最快使网络瘫痪。因此，短时间内，径线中的换乘站对网络弹性的影响较大，而长时间的失效状态下，环线换乘站引发的级联失效会使网络最快瘫痪。这可能是因为环线中的换乘站往往具有更大的连通性，与其他节点的紧密程度较高，一旦失效波及 的站点较多，具有很大安全隐患。

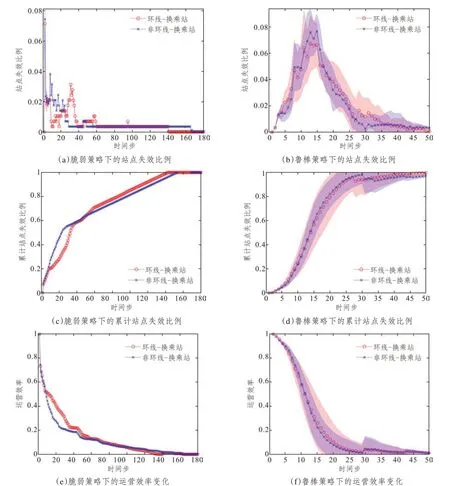
图7 换乘站不同策略下的网络弹性变化（阴影区域为标准差）Fig.7 Network resilience changes under different strategies of transfer stations

后两种场景下攻击相同换乘站，将环线换乘站的失效阈值提高0.5（即增加换乘站鲁棒性），ΔC= -0.5。同理分析非环线换乘站，结果如图7（b）、（d）、（f）所示。在对换乘站进行保护的情况下，径线上的换乘站会使网络崩溃的更快，失效高峰也最大，而环线换乘站在受到保护策略后会使网络具有较好的鲁棒性。

之后分析相应的弹性恢复阶段，站点恢复顺序分为两种：①先恢复所有环线上的换乘站，再恢复非环线换乘站；②先恢复所有非环线上的换乘站，再恢复环线换乘站。实验结果如图8所示，顺序一弹性为0.70，顺序二弹性为0.69，二者差别不大。这表明换乘站失效状态下的网络恢复性能相当，为更好提高网络弹性，还是应将关注点放在预防失效阶段，加强地铁系统中重要区域的风险监管。

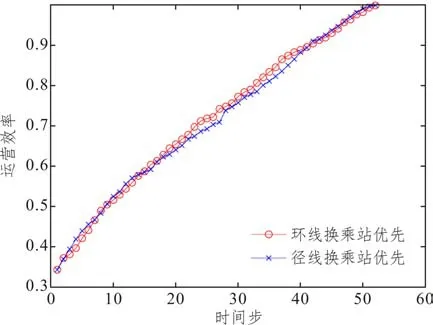
图8 环线和径线换乘站优先恢复下的网络弹性变化Fig.8 Network resilience changes under priority recovery of transfer stations on circle and diameter lines

2.3 面向线路的中断-恢复策略

针对北京地铁特有的两条环线和多条径线组合成的网络结构，分别选择两条环线10号线、2号线与两条径线4号线、1号线作为研究对象，基于改进的级联失效模型对整条线路减少脆弱性和增强鲁棒性下的级联效应情况进行对比分析。设置初始节点的干扰强度K=2.4，随机选择一个站点施加干扰。针对某种线路上站点增大脆弱性的情况，实验结果如图9（a）、（c）、（e）所示。整体上，两条环线的失效程度均大于径线。10号环线最先达到失效高峰，而2 号环线最快使网络瘫痪，并且运营效率也下降最快，4号径线则比1号径线使网络更易失效。

相应线路的站点增强鲁棒性的实验结果如图9（b）、（d）、（f）所示。与增大脆弱性的实验相比，两条环线在增强鲁棒性的策略下对网络弹性的提升明显，级联失效高峰大大降低，高峰时间和网络瘫痪时间均得到延缓并低于径线，如图9（b）所示。其中，2 号线保护之后对于网络鲁棒性能的提升较明显，网络瘫痪时间大大延后。因此，靠近中心的环线其鲁棒性的升高对网络的整体性能提升较明显，收到的效益也更高。在实际中，应有针对性地对其保护，将有限的资源进行合理分配。而在地铁网络初始规划和不断建设过程中，对线路和轨道网的规划也应该注重线路的拓扑结构等，注重环线与径线等不同线路形式结合下的网络规划选址。

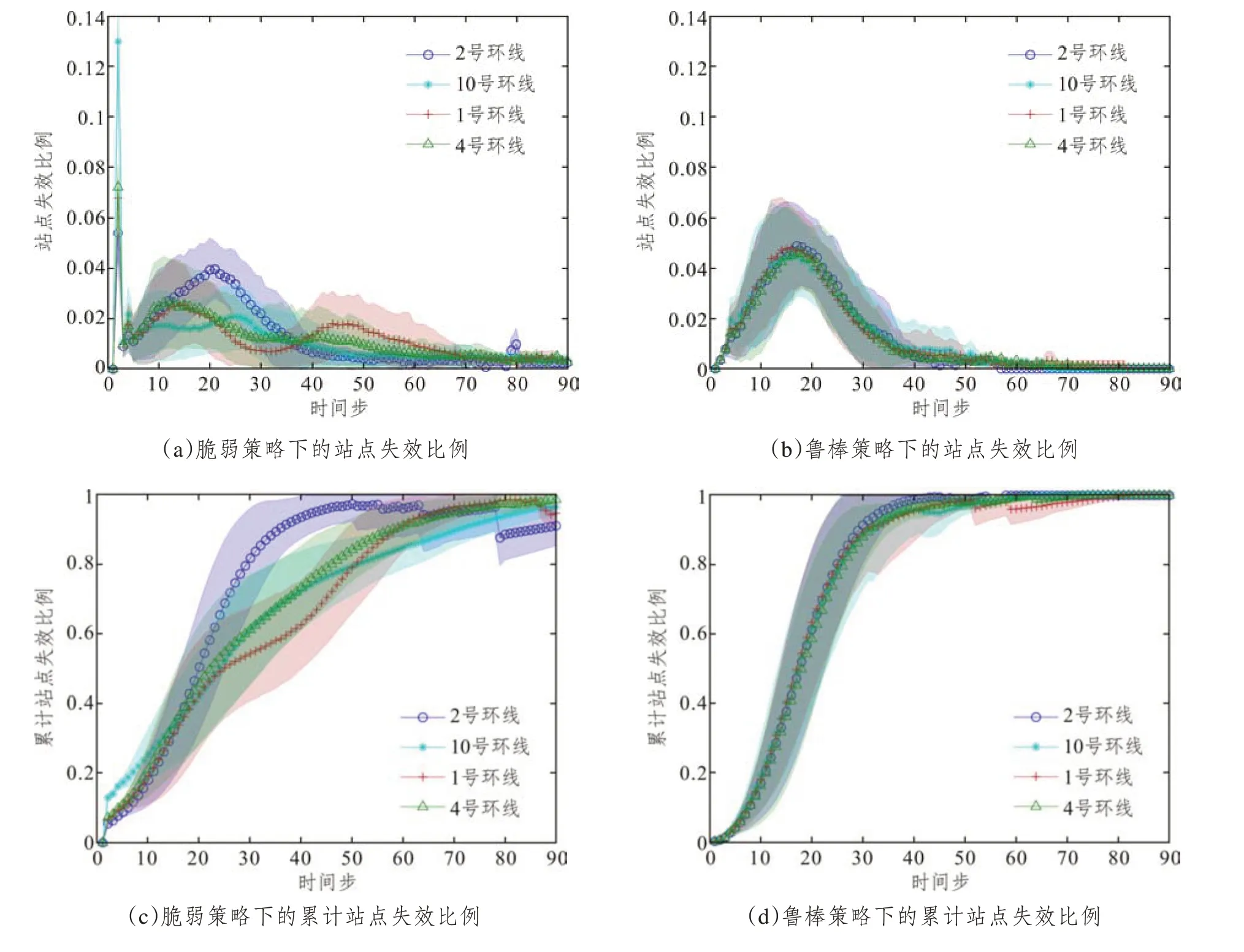
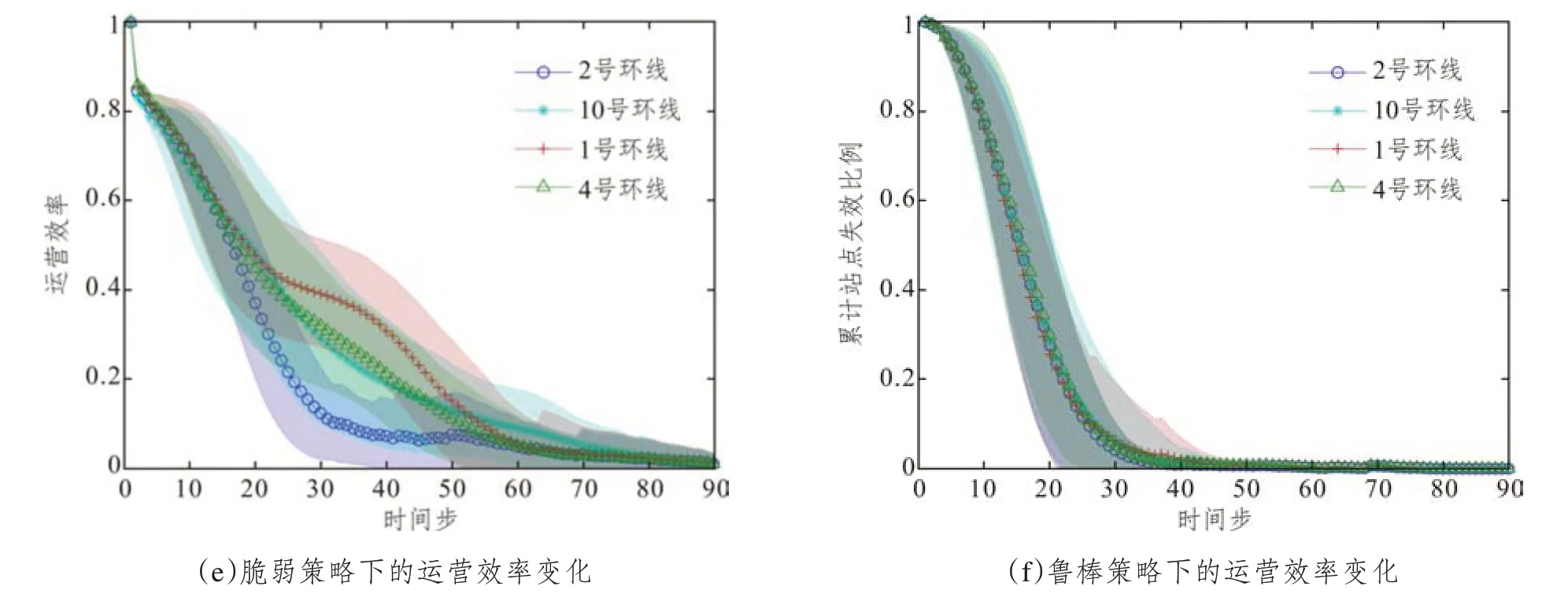
图9 各线路不同策略下网络弹性变化（阴影区域为标准差）Fig.9 Network resilience changes under different line strategies

之后分析相应的弹性恢复阶段，顺序一先恢复所有环线，再恢复剩余径线；顺序二先恢复所有径线，再恢复剩余环线。实验结果如图10 所示，顺序一弹性值为0.78，顺序二弹性为0.76。优先恢复环线可以使网络的弹性值提升，但效果不明显。因此，针对环线结构的失效和恢复情况，若要提高网络整体弹性，从而降低级联失效的破坏程度，还是应尽可能将系统资源放在运营维护和监管上，从开始阶段就防止网络失效的发生比瘫痪后的及时恢复所付出的代价更低，收到的效益也更高。

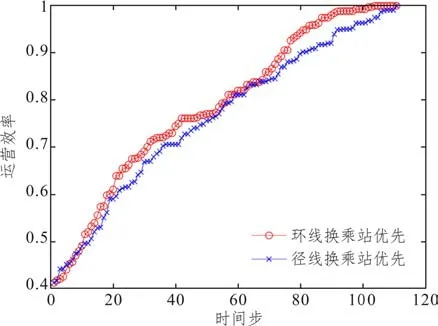
图10 环线与径线站点优先恢复下的网络弹性变化Fig.10 Network resilience changes under priority recovery of circle and diameter line stations

3 总结

本文主要针对地铁网络中独特的环线结构，在受到外界干扰后，环线对网络整体弹性变化产生的影响，尤其在级联失效情形下起到了何种作用进行了深入分析。以北京市地铁网络为例，基于图论建立拓扑网络模型并结合实际客流数据，采用改进的耦合映像格子模型从站点和线路两个角度研究了网络中断和恢复的全过程。仿真结果表明环线结构在网络性能的降低和恢复阶段均具有重要的作用，环线上的站点失效引发的级联失效反应更加剧烈，也使网络最快发生瘫痪，尤其是换乘站点的失效（如车公庄站和东单站）。而在恢复时优先恢复环线上的站点可以使网络更快地回到正常状态，网络整体具有更高的弹性值。并且在多环线网络下，越靠近中心的环线应受到重点保护，如北京地铁2 号线。此外，径线中的换乘站点也很重要，它起到了连接郊区和中心的支点作用，一旦失效整条支线都将受到严重影响。该研究为目前地铁网络的建设、线路选址提供了从全局角度出发的参考，有效指导实际运营中管理人员对环线结构的监管和保护，也为复杂网络理论中有关环线的拓扑结构特性的研究提供了重要补充。在未来可以继续探究，如何根据各种相关指标确定具体站点和线路的鲁棒性或脆弱性值以及所对应的状态更新值，以及可能引起的不同级联失效情况。