考虑列车加开的技术站车流接续模型

薛 锋，范千里，周 琳，陈崇双

（1.西南交通大学，交通运输与物流学院，成都 611756；2.综合交通大数据应用技术国家工程实验室，成都 611756；3.综合交通运输智能化国家地方联合工程实验室，成都 611756；4.宁波港铁路有限公司，宁波 315200；5.西南交通大学，数学学院，成都 611756）

0 引 言

随着高速铁路的快速发展，普速铁路的运力逐渐得到释放，同时社会对铁路货车的周转效率以及技术站的工作组织都提出了更高的要求。目前，我国铁路运输中常见的两种货车集结模式为定编集结和定点集结，但随着铁路货运市场化的发展，两种货车集结模式均呈现出一定的不适应性。在定编集结模式下，货物运输在时间上具有较大的不确定性，无法达到客户对货运时效性和准确性的要求；在定点集结模式下，若列车没有达到最小编成辆数要求，会造成能力浪费和车流积压问题。若在适当情况下在技术站加开列车，则能够减少货车的平均在站停留时间，加速货车周转，有效缓解车流积压问题。因此，非常有必要研究考虑列车加开情况下的技术站车流接续优化问题。

目前对于列车加开情况下的技术站车流接续优化研究相对较少。在列车加开方面，基本围绕列车加开对技术站集结系统的影响展开，王如义[1]运用仿真的方法，探讨了最小编成辆数的变化对加开以及丢线次数的影响；李静等[2-3]为避免丢线情况的产生，分析了相邻出发列车进行车流分配对车辆集编排队系统性能的影响，从而实现车辆集编排队系统优化；胡洋[4]从经济效益的角度出发，引入博弈分析方法，对高速铁路加开方案进行了分析。在车流接续优化方面，现有的研究较为丰富，薛锋等[5]引入修复因子，给出了欠轴列车发车的必要条件，并以车辆在站停留时间最短为目标，建立了技术站车流接续优化模型；赵军[6]构建了具有紧凑结构的技术站作业优化整数规划模型，并依据各模型特点设计了有效的精确算法和近似算法；黎浩东[7]结合市场经济因素，将出发列车的运输收益考虑到计划编制中，构建了具有鲁棒性的编组站阶段计划配流模型，并利用了多种算法进行求解。国外的专家学者同样也对列车的加开进行了研究，但大多数集中于路网层面。Cacchiani[8]以在不打乱现有时刻表的基础上尽可能地引入更多的货物列车为目标，提出整数线性规划模型，并基于该模型设计了拉格朗日启发式算法，进行了实例分析；Burdett[9]针对安排加开列车服务（Scheduling Additional Train Services , SATS）问题：①考虑了加开列车与现有列车同属于和不属于相同运营单位时，二者对铁路基础设施的竞争；②考虑了加开列车与现有列车（二者可属相同或不同运营商）之间对铁路基础设施的竞争，并设计了相关的智能算法进行求解。此外，大多数研究也同样集中于技术站的配流优化，Alikhani-kooshkak[10]为了同时研究列车编排和列车路线的问题，以总利润、客户满意度、调车作业总量、未充分利用的列车数为目标函数，建立列车编排综合问题的多目标数学模型，并设计了模拟退火算法进行求解；Bohlin[11]针对多级列车编组的数学优化问题，提出了两个优化模型并进行了评估，第一个是基于列的整数规划模型，第二个模型是第一个模型的简化形式，它是弧形索引整数线性规划，与第一个模型具有相同的线性规划松弛度，并用一个实例将二者进行了比较分析；Boysen[12]、Alexander[13]等建立混合整数规划模型，利用启发式算法计划了调车机车最佳路线，给出了调车线集结货车的最优编组决策。

综上所述，虽然目前对车流接续的研究较多，但在列车加开方面，仍缺乏深入研究。本文考虑技术站可能出现的拥堵情况，探索在车流接续优化过程中实施列车加开作业的可行性，应用推拉理论分析技术站加开列车的条件，建立考虑列车加开的技术站车流接续模型，以便提高技术站的车流组织效率。

1 技术站列车加开条件分析

为加快货车周转效率，在车流不拥堵的情况下，可以进行配流计划的优化，而在车流拥堵的情况下，可以考虑更为灵活的配流模式，即在列车加开作业的基础上进行车流接续优化。因此，首先需要判断技术站的拥堵情况，当拥堵情况严重需要加开列车时，再分析进行列车加开存在的冲突，判定是否能进行列车加开作业。

1.1 技术站列车加开判定

技术站进行列车加开是由于技术站内出现了拥堵的情况，拥堵程度过高时，需要进行列车加开作业。为确定技术站的拥堵情况，首先对技术站各子系统空间上的负荷进行分析。

1.1.1 技术站负荷的确定

由于到达列车进入到达场、到达列车解体进入调车场、列车集结完毕进入出发场后，都需要占用相应的股道，因此可以根据车站股道的基本固定使用方案，将技术站各子系统的负荷情况定义为车辆对股道的占用情况，由此可得各子系统负荷[14,15]如下所示：

式中：ρi,当i=1,2,3 时分别表示到达场负荷、调车场负荷、出发场负荷；mi，当i=1,3时分别表示到达场、出发场列车占用的股道数，当i=2 时表示调车场全部股道占用的总车辆数；Mi，当i=1,3 时分别表示到达场、出发场的总股道数（不包含机走线），i=2时表示调车场全部股道的总容车数。

同时，若出发场股道全部被占用，即出发场负荷为1 时，加开的列车无法出发，可以判定无法进行列车加开作业，由此可得列车加开的条件，即：

1.1.2 技术站推拉效应分析

单一运用调车场内部的负荷情况判定技术站的拥堵情况并不准确，例如虽然调车场内部负荷不大，但到达场车流大量聚集并进入调车场，同时出发场出发作业减少，带动调车场进入出发场的车流减少，也会逐渐导致调车场内部的车流堆积。因此，为准确表示技术站的拥堵情况，可以将到达场、调车场、出发场三者负荷之间的关系视为一种推拉效应。

以交叉弹性系数为基础，建立到达场-调车场-出发场的推动与拉动效应模型分别为：

（1）列车作业顺序方向，到达场-调车场-出发场之间的推动效应模型：

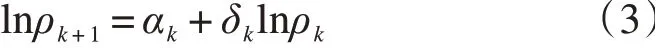
式中：αk,当k=1,2 时都表示常参数[16]；δk,当k=1,2时分别表示到达场与调车场之间，调车场与出发场之间的推动效应系数。

（2）列车作业逆序方向，出发场-调车场-到达场之间的拉动效应模型：

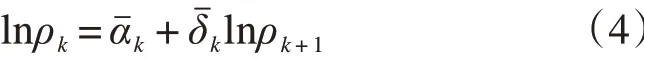
式中：αˉk,当k=1,2 时都表示常参数[16]；δˉk,当k=1,2时分别表示调车场与到达场之间，出发场与调车场之间的拉动效应系数。

根据推拉理论，当到达场-调车场的推拉效应大于调车场-出发场的推拉效应，即进入车场的车辆数大于离开车场的车辆数，且二者差值大于某个规定的阈值μ时，可以判断技术站内会出现拥堵的情况，需要进行列车加开作业，即：

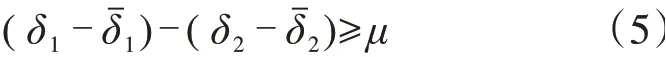
式中：μ表示判断技术站是否会出现拥堵的阈值。

列车加开的去向可以根据调车场内的存车数进行判断。对比调车场内各方向的货车，其中调车场内货车数量最多的方向，可以作为加开列车的去向，而最终的加开列车方向需要根据优化情况进行选择判断。

1.2 技术站列车加开存在的冲突分析

如果在技术站加开列车，需要明确加开列车与既有列车技术作业及既有列车运行图之间的冲突，当这些冲突无法消除时，就无法进行列车加开作业。

1.2.1 与现有列车技术作业的冲突

（1）加开列车与后续列车之间的冲突

由此可得，当存在一台编组调机时，为避免加开列车与后续列车作业计划之间的冲突，加开列车最晚编组开始时刻应满足如下约束条件[17]：

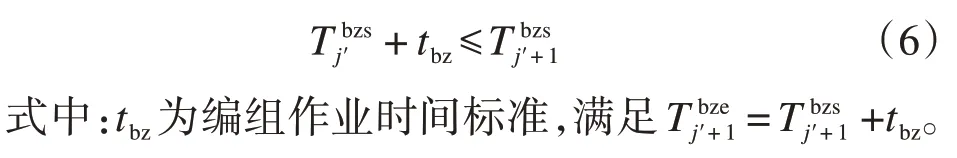
若存在2台编组调机，加开列车与后续列车之间存在的冲突如图2 所示。由图2 分析可得，加开列车与后续列车可能存在两类冲突：

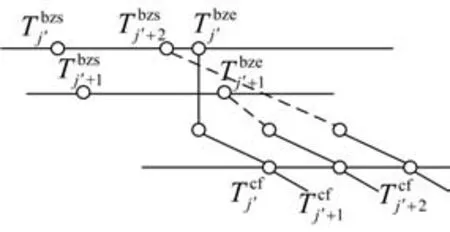
图2 两台编组调机时加开列车与后续列车的冲突示意图Fig.2 Diagram showing conflict between the additional and subsequent trains when two formations are transferred

由此可得，当存在两台编组调机时，为避免加开列车与现有作业计划之间的冲突，加开列车需要满足如下约束：

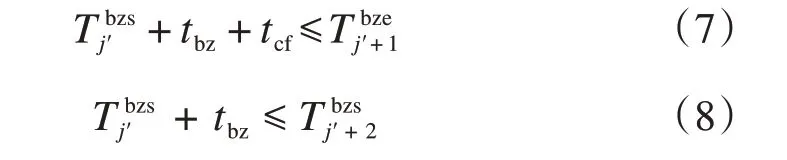
式中：tcf为出发作业时间标准。

（2）加开列车与前续列车之间的冲突

若存在两台编组调机，加开列车与前续列车之间的冲突如图3 所示。分析可得，当加开列车j′的编组结束时刻Tbzej′早于前续出发列车j′-1 的出发时刻Tcfj′-1时，可能会发生以下两种情况：一是加开列车无法按照规定的出发时刻发车；二是前续列车无法按照列车运行图规定的时刻出发。

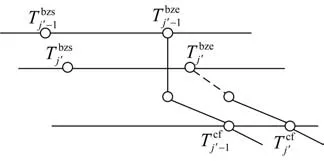
图3 两台编组调机时加开列车与前续列车的冲突示意图Fig.3 Diagram showing conflict between the additional and preceding trains during the transfer of two formations

由此可得，当存在两台编组调机时，为避免加开列车与技术站现有作业计划之间的冲突，加开列车需要满足如下约束[17]：

1.2.2 与既有列车运行图之间的冲突

加开列车是否开行同样需要考虑与既有列车运行图之间的冲突，保证加开列车与既有列车运行图都能够按照规定运行，需满足的条件为加开列车与同方向的出发列车之间的间隔时间应满足追踪列车间隔时间，如图4所示。

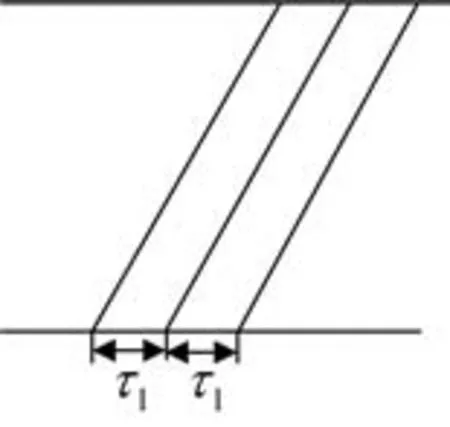
图4 加开列车与列车运行图的冲突示意图Fig.4 Diagram showing conflict between the additional trains and the train operating chart

由此可得，为避免加开列车与既有的列车运行图出现冲突，需要满足如下约束：

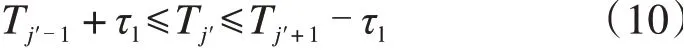
式中：τ1表示追踪列车间隔时间。

2 考虑加开列车的技术站车流接续模型

2.1 参数及目标函数

为了简化该模型，现指定创建模型的基本条件和假设：

（1）2台调机进行解体作业，1台调机进行编组作业；

（2）技术站内到发场、调车场的各股道均达到作业标准；

（3）对调机出现的故障、整备及维修情况不予考虑；

（4）对无调中转车及其在站的甩挂作业不予考虑。

建模所需参数的符号及其含义如表1所示。

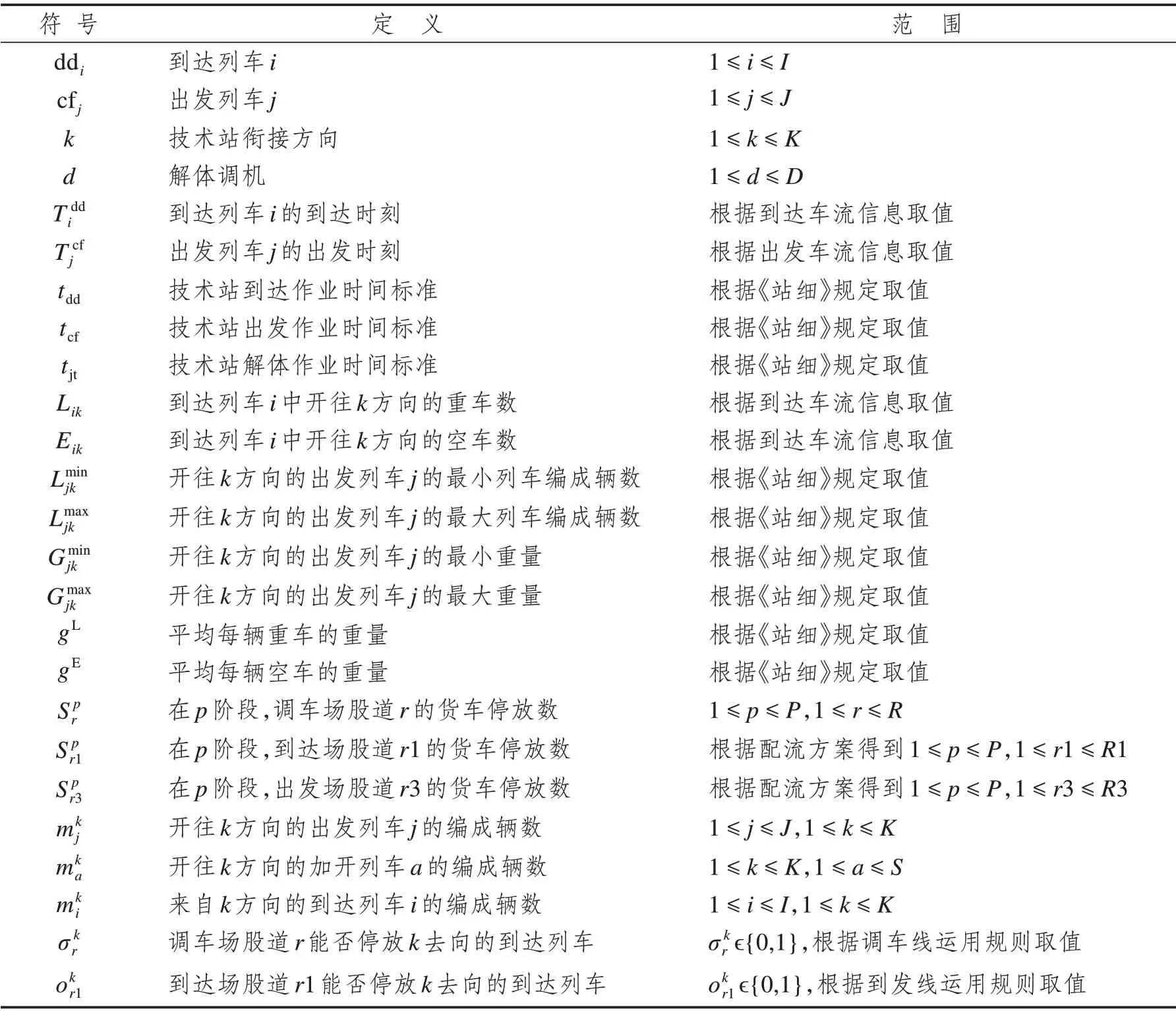
表1 参数及其符号说明Tab.1 Description of parameters and their symbols

建模所需变量及其符号说明如表2所示。

表2 变量及其符号说明Tab.2 Description of variables and their symbols

续表2

对技术站进行列车加开是为了提高货车的周转效率，目标函数可以参照传统的技术站配流模型设置为货车在站总停留时间最短[19,20]，由于本模型中进行了列车加开作业，因此需要额外考虑加开列车对技术站出发列车数量的影响。

综上，设置目标函数如下所示：

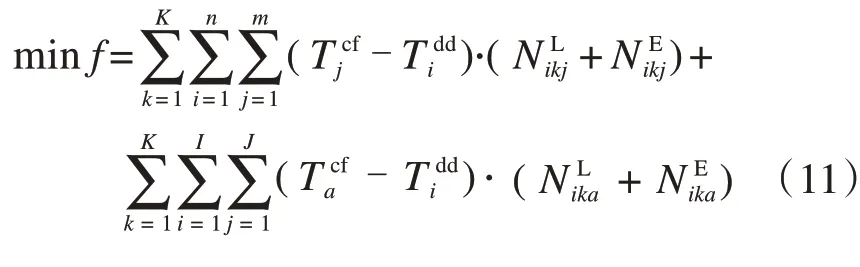
2.2 模型的约束条件

在优化模型中，除了要满足配流模型中的传统约束和其他逻辑约束[21,22]以外，加开列车对原有约束的影响也需要考虑在模型约束中。另外，由于本文在列车加开判定中涉及了技术站内部到达场、调车场以及出发场的容量情况，因此，还需要考虑车场容量约束。

（1）解体作业约束

①任意一列到达列车ddi的解体作业只能由一台调机完成：

（2）编组作业约束

由于列车加开作业，对编组作业约束造成了大量的影响，因此还需考虑加开列车对原有约束的影响。

①任意一列加开列车编组完成时刻需小于出发时刻减去出发作业时间：

②对于加开列车a而言，需要满足与其他出发列车的编组作业不存在冲突的条件：

（4）编成辆数约束

现有的研究中，对列车满轴的约束分为两类：一是不对重空车进行区分，直接采用换长进行约束；二是对重空车进行区分，分别对出发列车的编成辆数以及列车的重量进行约束。在本文中为描述货车转移过程，采用第二种约束方法，即分别对出发列车的编成辆数以及列车的重量进行约束。因此可以得到任一出发列车cfj的长度及重量的限制约束：

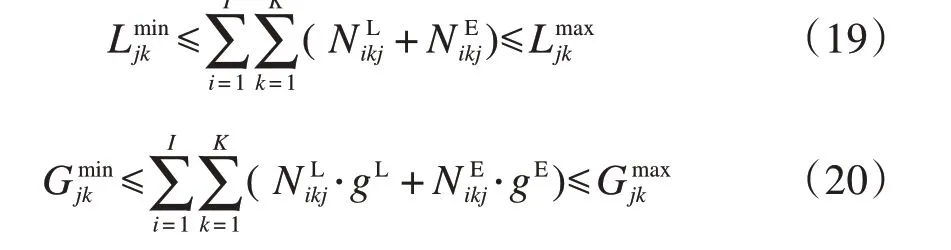
（5）车流接续约束

任意一列出发列车cfj只能吸收解体结束时刻小于该出发列车的编组开始时刻的到达列车车流：

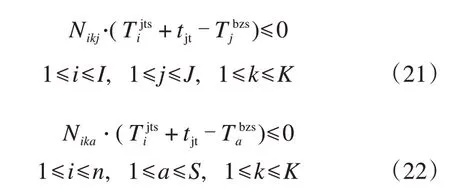
（6）加开列车冲突约束

基于加开列车条件的分析，可以得到加开列车冲突约束：

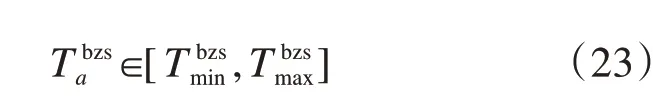
（7）技术站子系统容量限制约束

由于技术站子系统的负荷会随着时间出现变化，为准确描述技术站的负荷情况，我们需要将整个优化阶段进行划分，以调车场、到达场、出发场内的列车数量变化的时刻作为划分阶段的标准，可以得到各子系统的股道状态更新[23,24]如下所示：

①调车场子系统容量约束

对于调车场内任意一条股道，股道占用随着解体列车的进入而增加，随着集结列车的牵出而减少。因此，需要确保在任一时刻车辆数都在其容量约束之内，并且确保货车的去向与调车场股道的使用方案相匹配：

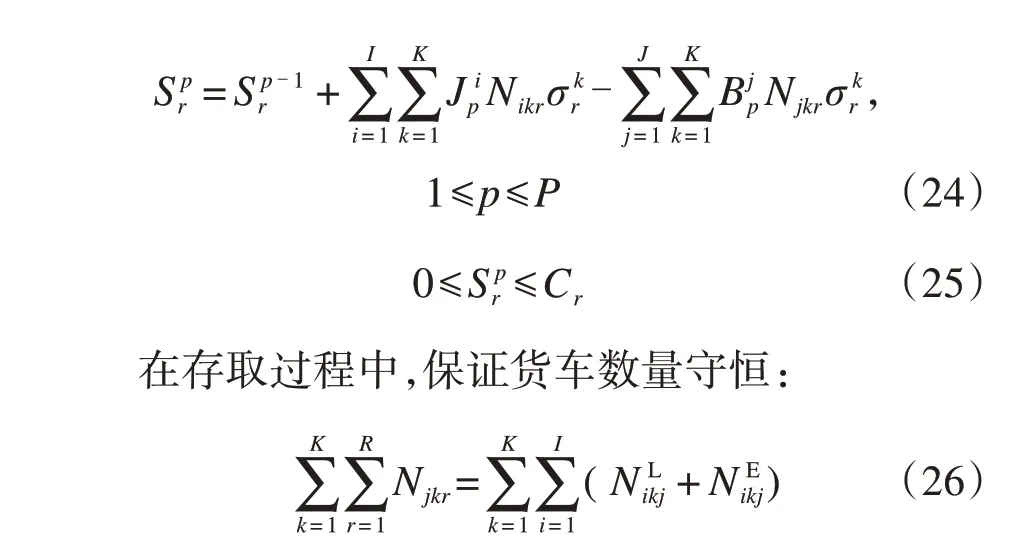
②到达场子系统容量约束

对于到达场内的任一股道，占用的股道随着到达列车的到达而增加，随着列车的解体而减少，需要确保到达场的股道占用在每一阶段都在股道的容量约束之内：

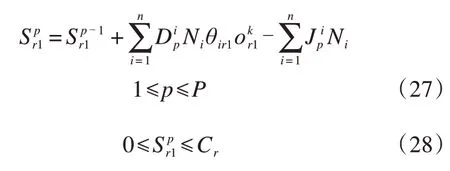
每一到达列车ddi只能占用一条到达场股道r1：

③出发场系统容量约束

对于出发场内的每一条股道，占用的股道随着列车集结完成牵出而增加，随着出发列车的出发而减少，需要确保出发场股道占用在每一阶段都在股道的容量约束之内：

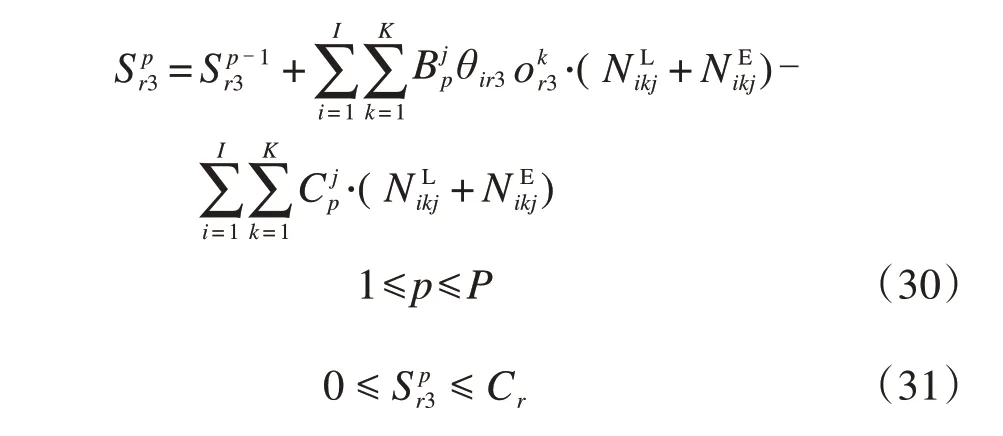
每一列出发列车cfj只能占用一条出发场股道r3：

2.3 模型的求解

2.3.1 模型的分解

车流接续问题本身属于NP 完全问题，与既有研究相比，本文额外考虑了列车加开和股道运用问题，无疑加大了模型的复杂程度。为此可以将模型进一步细分为车流接续子问题和股道运用子问题。

值得注意的是，此处的股道运用子问题并不是一个单独的优化问题，由于需要确定是否进行列车加开作业，需要对技术站内部的拥堵情况进行确认，涉及了技术站的到达场、调车场、出发场内的股道运用情况，但并没有对其进行过多的优化，只是为了便于求解，将其进行了分解并设置了相应的目标函数，但这个目标函数并不作为整个模型的优化目标。

（1）技术站车流接续子问题

当结合技术站负荷情况进行车流接续优化时，进行加开作业后，列车的解体编组顺序会发生改变，那么到达列车的最早开始解体时刻以及出发列车的最晚开始编组时刻也会发生改变，不利于确定技术站各子系统的负荷以及列车加开时刻。

若不改变列车的解体编组顺序，根据股道运用子问题的结果，当列车加开时间处于1.2 节得到的基本时间窗内时，加开车次只会对调车场的车流输出以及出发场的车流输入造成影响。因此，对于车流接续子问题的求解，可以在确定列车解体编组顺序的基础上求解车流来源，再结合技术站负荷情况来确定加开车次。

因此，技术站车流接续子问题模型确定为：

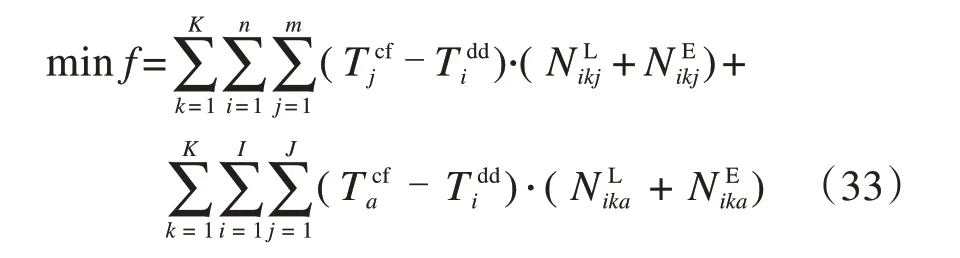
s.t. 约束式（12）～（23）。

（2）股道运用子问题

确定不同阶段股道运用是为了得到技术站负荷情况，为后续加开列车的确定奠定基础。为便于模型求解，可以考虑将股道运用子问题的目标函数设置为列车占用的调车场股道数目最少，再根据车流接续子问题得到的列车解体编组顺序以及车流来源情况，结合相应算法求得到达场和出发场的股道占用情况。

因此，技术站股道运用子问题模型确定为：

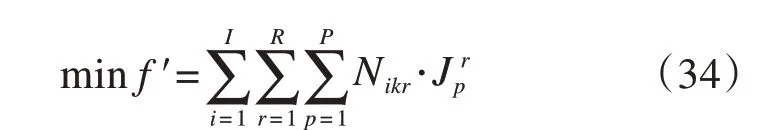
s.t. 约束式（24）～（32）。

2.3.2 求解算法

遗传算法作为一种模拟生物进化的高效寻优算法，在求解多约束非线性规划问题时能发挥其全局寻优的优势, 被广泛运用于技术站车流接续的研究中。

（1）车流接续子问题

①染色体编码：考虑到车流接续问题的特点，采用整数染色体编码，以解编顺序为基因构成染色体,到达列车的解体顺序设置为jt=[ddi,ddi′,ddi″,…,ddin]，出发列车的编组顺序为bz=[cfj,cfj′,cfj″,…,cfjn]，构成的染色体为p=[jt,bz]。

②初始种群的产生：设种群规模为e，解体顺序初始种群J=[jt1,jt2,…,jtz]，编组顺序初始种群B=[bz1,bz2,…,bze]。结合既有文献的方法[6]，当相邻两列出发列车满足调整解编顺序的条件，即前一列出发列车的待编时间足够后一列出发列车进行编组作业，则可以对列车编组顺序进行编码，确保生成合法且竞争优势较大的初始种群。

根据当前编组顺序初始种群得到初始种群P[25]的步骤如图5所示。

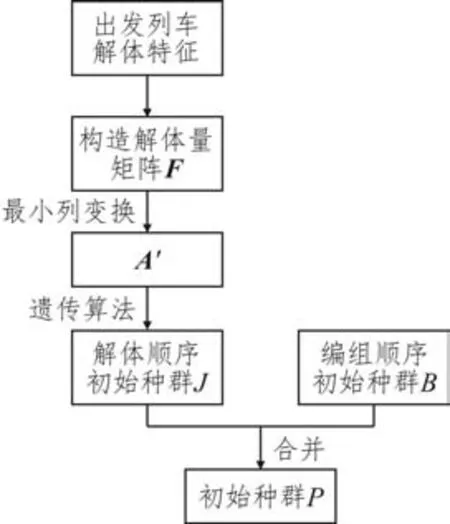
图5 初始种群产生步骤Fig.5 Initial population generation steps

③适应性函数：采用目标函数（11）作为适应性函数。

④遗传算子：依照联赛选择规则筛选出具有高适应性优势的个体。由于交叉及变异处理编组顺序初始种群时容易产生不合法且求解质量低的个体，因此需对解体顺序初始种群进行处理。其中，交叉算子使用了基于位置的杂交算子，变异算子采用了散播变异算子。

⑤终止规则：将进化代数作为算法的停止条件。

⑥静态配流：广义静态配流[26]。

（2）股道运用子问题

①染色体编码及初始种群的产生：技术站内各子系统负荷变化的节点与技术站内作业过程相关，例如到达场负荷发生变化的节点为到达列车到达并完成解体。因此，可以对该子问题的染色体做出如下设计：

在到达场股道中，设到达列车共有n列，对任一到达列车ddi，染色体中位置3i-2用于表示到达列车接入股道的阶段p1s，染色体中位置3i-1 用于表示到达列车占用的股道r1s，染色体中位置3i用于表示到达列车完成解体作业所在的阶段p2s。到达场染色体情况如图6所示。

图6 到达场染色体示意图Fig.6 Schematic diagram of arrival field chromosome

在调车场股道中，假设技术站衔接了K个方向，对任一完成解体作业后进入调车场的到达列车dds，其编组内容分别为k1方向货车10 辆，k2方向货车15辆。染色体中位置3i+(s-1)(K+2)+1设置为到达列车完成解体作业所在的阶段，染色体中位置3i+(s-1)(K+2)+k1-1 设置为k1方向货车所占用的股道，染色体中位置3i+(s-1)(K+2)+k2-1设置为k2方向货车所占用的股道。调车场染色体情况如图7所示。

图7 调车场染色体示意图Fig.7 Schematic diagram of shunting yard chromosome

在出发场股道中，对任一出发列车cfi，染色体中位置(K+6)i+3c-2 表示出发列车完成解体作业所在的阶段，染色体中位置(K+6)i+3c-1 表示出发列车占用的出发场股道，染色体中位置(K+6)i+3c表示出发列车出发时刻所在的阶段。出发场染色体情况如图8所示。

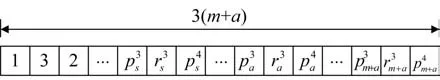
图8 出发场染色体示意图Fig.8 Schematic diagram of departure field chromosomes

②适应性函数：采用目标函数（30）作为适应性函数。

③遗传算子：对于杂交算子而言，虽然技术站股道运用子问题的染色体G由不同的部分组成，但不同染色体的结构都是相同的，在进行杂交作业后并不会在结构上出现非法个体。但可能会出现股道容量超出限制的情况，此时应停止杂交操作。

对于变异算子而言，由于在技术站股道运用子问题的染色体G中，实际变量只有各子系统占用股道的数量，因此，只对此变量进行变异操作。同理，需要判断是否出现股道容量超出限制的情况。

④终止条件：算法终止的条件设置为进化代数。

2.3.3 算法的基本思路

结合技术站车流接续子问题及技术站股道运用子问题的算法流程，可以得到以下算法思路：

①求解技术站车流接续子问题，得到列车的解体编组方案以及配流方案。

②结合①中结果，求解股道运用子问题，得到到达列车、货车以及出发列车占用到达场、调车场以及出发场的股道情况，以此反映技术站的负荷情况。

③从阶段开始时刻观察技术站的负荷是否有超过阈值的情况，若没有，则结束算法，输出配流方案，否则应继续进行算法。

④将第一段技术站总体负荷超过阈值的时间作为调整时间，结合1.2 节中关于技术站加开列车的条件分析，得到技术站内的列车加开时刻及加开去向。

⑤返回①中进行循环。

3 算例分析

3.1 算例背景

某技术站位于2 条铁路干线交汇处，到达场、调车场、出发场的股道数量分别为4 条、10 条、5条，各股道具体的有效长、换算容车数以及停靠货车去向要求如表3、4、5所示。

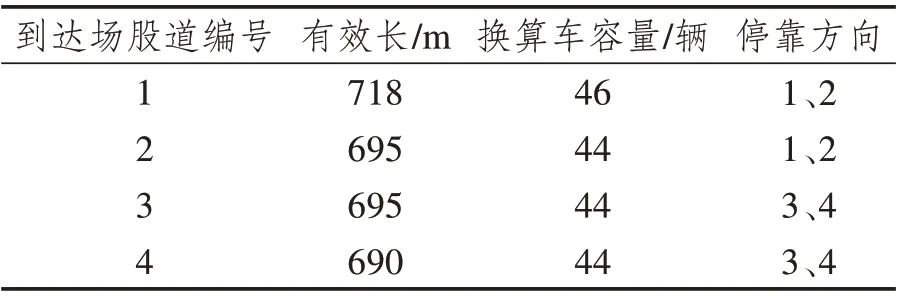
表3 到达场股道情况Tab.3 Arrival field strands

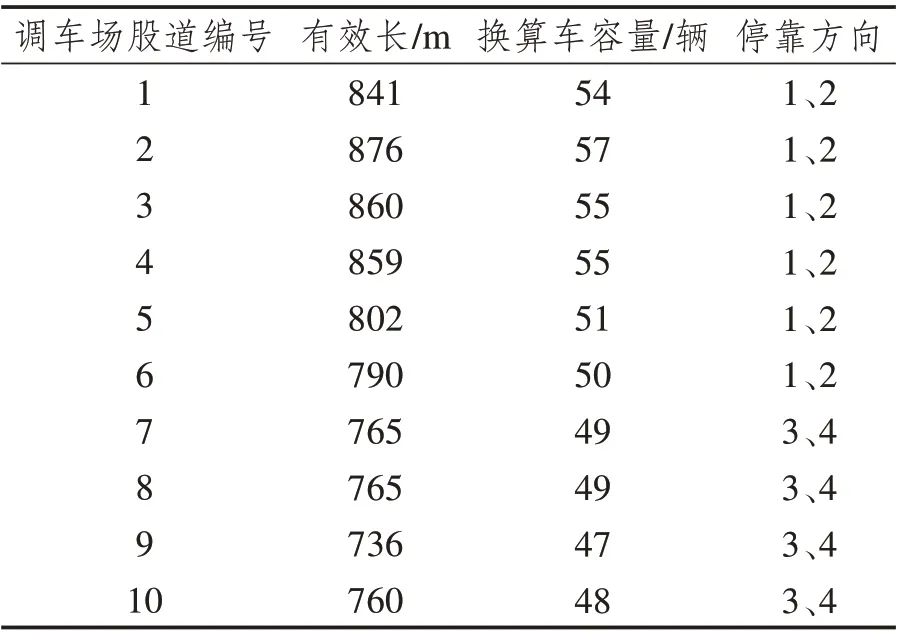
表4 调车场股道情况Tab.4 Shifting yard strand situation

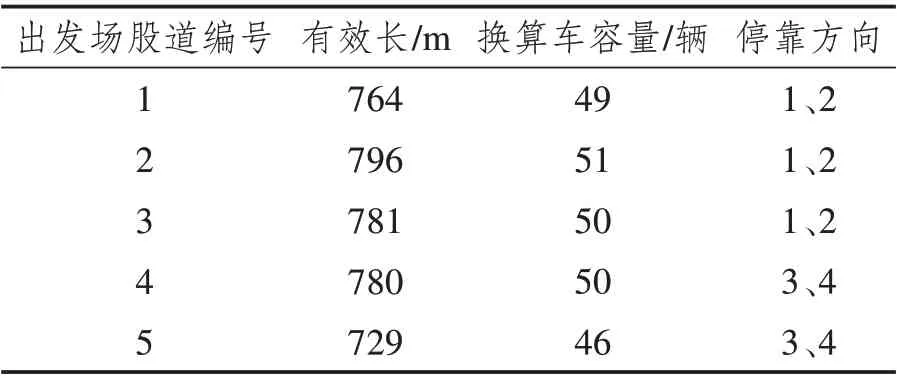
表5 出发场股道情况Tab.5 Departure field strand conditions

该站衔接东西2个方向，衔接区间长度分别为50 km 和55 km，列车旅行速度为100 km/h，追踪间隔时间为10 min。东西每个方向均有2 个去向，所有去向按照其所在的方向及远近顺序原则进行编号。因此，东西两个方向共4个去向，由远及近分别标记为1、2、3、4，5为排空方向。现选择8:00～12:00这一时间段，第一列到达的列车被记为10 000，该列车并非由真实的机车和货车组成的列车，而是由于上一阶段未被成功进行车流接续而造成的调车场残存车。值得注意的是，此列到达列车的到达作业时间以及解体作业时间都为0，而其余的到达列车会在计划到达时间内到达。技术站到达车流以及出发车流信息如表6、7所示。

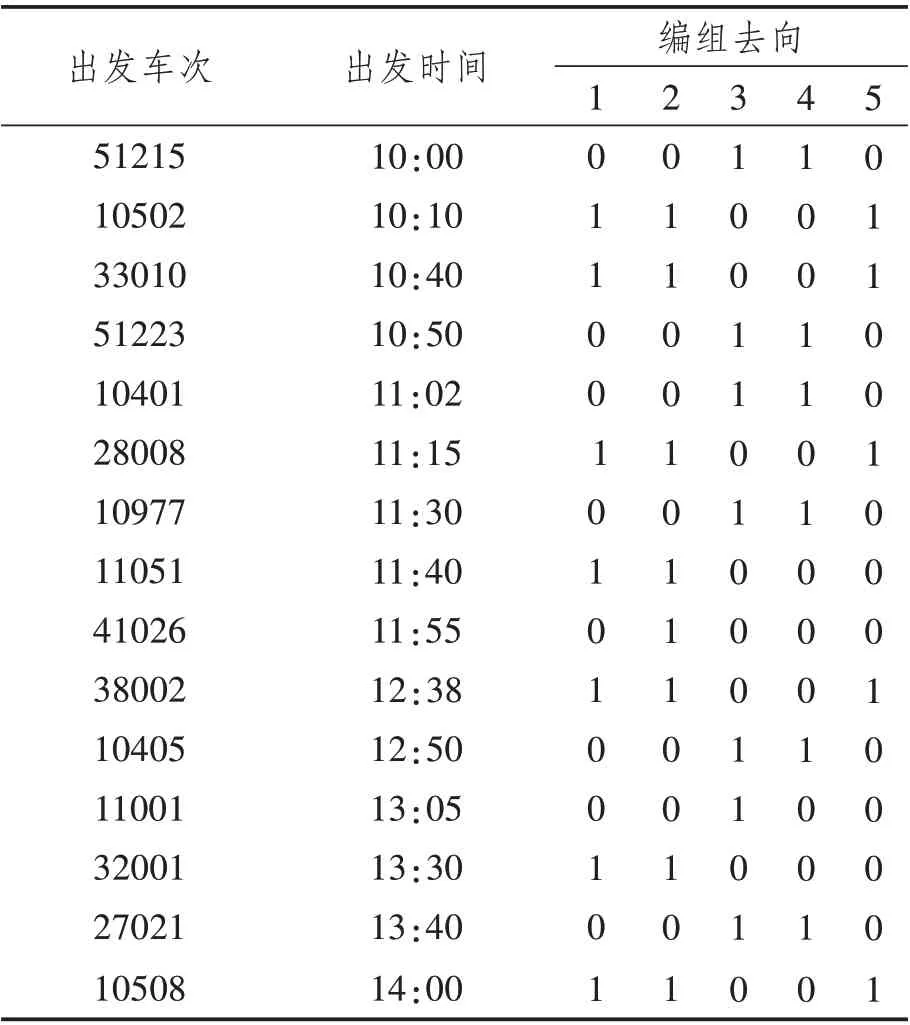
表7 出发车流信息Tab.7 Departure traffic information

技术站规定摘挂列车允许欠轴开行，其他技术作业时间标准及列车相关信息如表8所示。

表8 技术站作业时间标准及列车信息Tab.8 Technical station operation time standards and train information

3.2 算例求解

按照原配流方案先到先解体的原则，设置其解体顺序为[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]，编组顺序为[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]，结合前文中给出的技术站作业时间标准、到达以及出发车流，可以得到配流方案如表9所示。

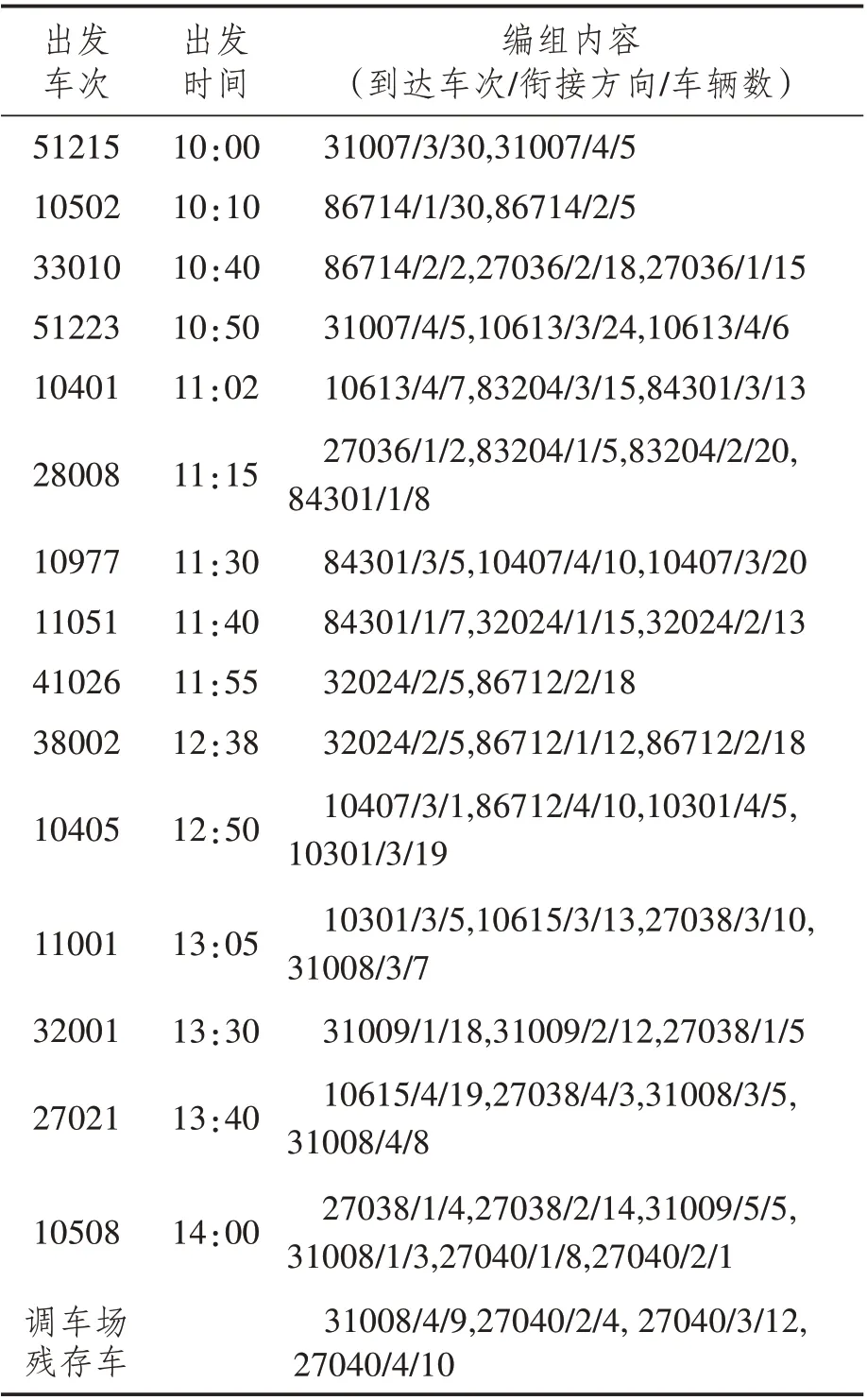
表9 优化前配流方案Tab.9 Flow distribution scheme before optimization

在原配流方案中，货车在站总停留时间为1 682.3 h，平均在站停留时间为191.2 min，到达场、调车场、出发场负荷情况以及技术站总体负荷情况如图9、10所示。

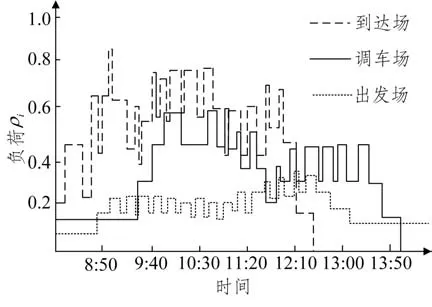
图9 到达场、调车场、出发场负荷情况Fig.9 Arrival yard,shunting yard,and departure yard load situation

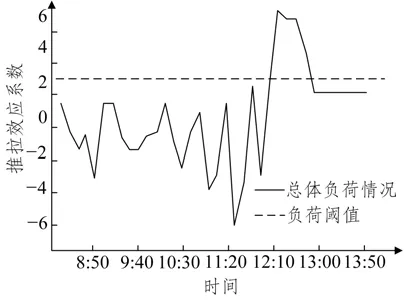
图10 总体负荷情况Fig.10 Overall load situation

分析现有的配流方案可以发现，到达场负荷从8:00 开始逐步增加，9:00 达到最大值，此后在较高水平范围内波动，从12:00 开始逐渐下降，12:30降低至0；调车场负荷在8:00至9:30维持在较低水平不变，随后逐渐增加，并在中等水平范围内波动，13:30 开始逐渐下降，14:00 降低至0；出发场负荷在阶段时间内变化平稳，持续在较低水平范围内波动，13:10 开始保持不变且不为0，说明阶段末仍有残存车。由于出发场能力限制，导致总体负荷增大，因此技术站总体负荷在12:10 以后存在超过阈值的情况，且在阶段结束后调车场仍存在残存车。

在现有配流计划的基础上，应用本文建立的基于列车加开的车流接续模型及算法，可以得到优化后的配流方案，具体配流方案如表10所示。

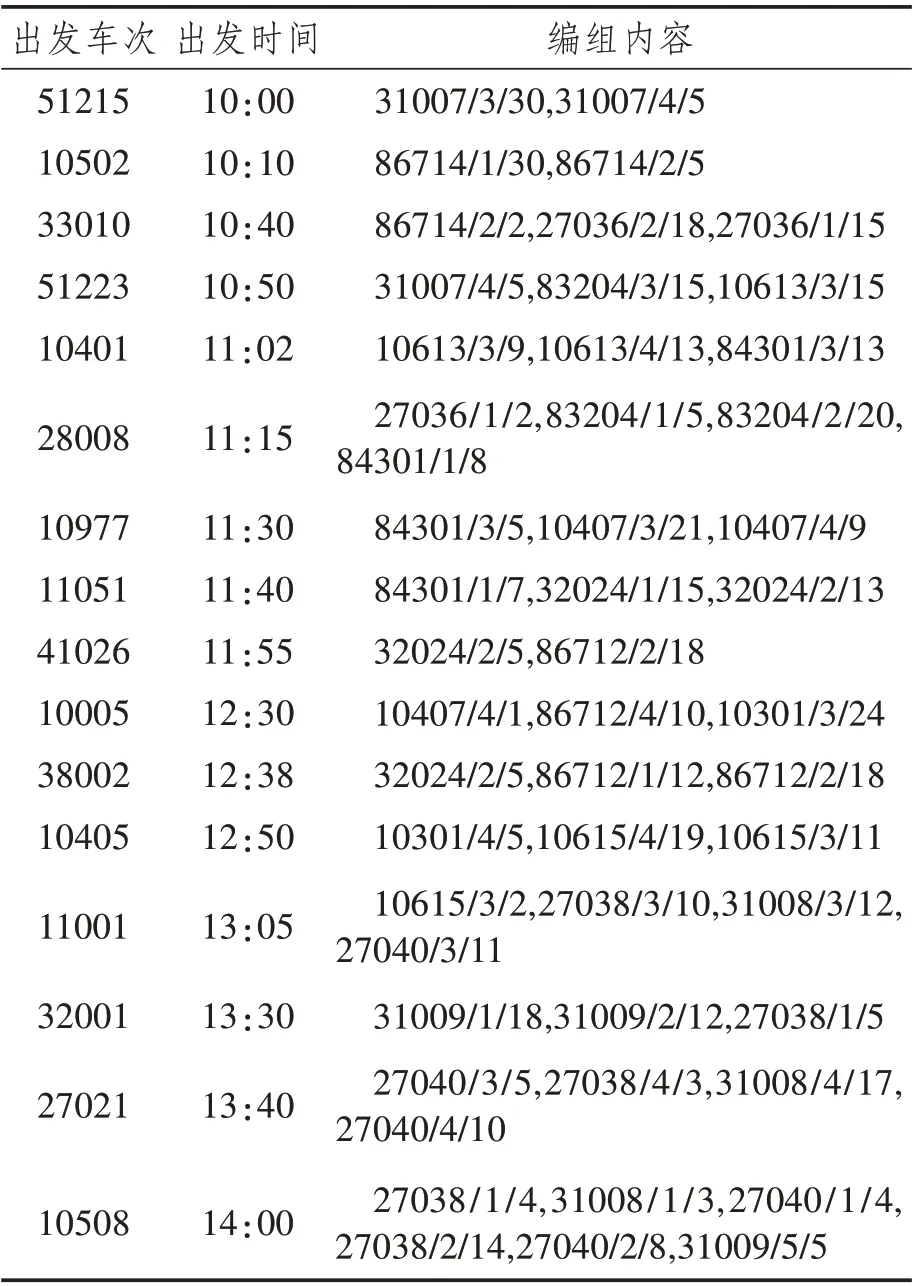
表10 优化后配流方案Tab.10 Optimized flow distribution scheme

在优化配流方案中，加开了10005 次列车，改变了列车的解体和编组顺序，到达列车的解体顺序优化为[1,2,3,5,4,6,7,8,9,10,11,12,13,14,15]，出发列车的编组顺序优化为[2,1,3,4,5,6,7,8,9,10,11,12,14,13,15,16]，使得货车在站总停留时间变为1 558.5 h，减少了123.8 h，平均在站停留时间变为177.1 min，减少了14.1 min。到达场、调车场、出发场的负荷情况以及技术站的总体负荷情况如图11、12所示。

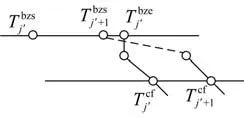
图1 一台编组调机时加开列车与后续列车的冲突示意图Fig.1 Diagram showing conflict between the additional and subsequent trains when a formation is transferred to a machine

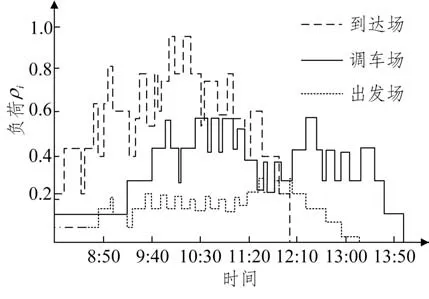
图11 优化后到达场、调车场、出发场负荷情况Fig.11 Load situation of arrival yard,shunting yard,and departure yard after optimization

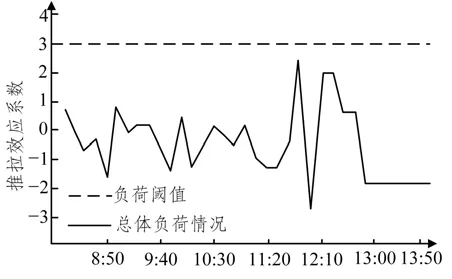
图12 优化后总体负荷情况Fig.12 Overall load after optimization

分析优化后的配流方案可以发现，到达场负荷较大的时间段集中在8:50 至11:00，之后迅速降低至0；调车场负荷在中等水平范围内持续波动，13:30 开始下降，14:00 降低至0；出发场负荷在较低水平范围内波动，13:10 降低至0。相较于原配流方案，优化方案的调车场负荷变化大致相同，到达场和出发场负荷对比同时间段均有所降低。图11 中，出发场负荷最终降低至0，说明了调车场在阶段末没有残存车，有效提高了货车的转移效率。优化方案中的技术站总体负荷有所降低，尤其是在12:30 加开了10005 次列车后，技术站总负荷大幅度下降至阈值以下，避免了技术站出现车流拥堵问题。

对比优化前后的配流方案以及技术站的负荷情况发现：

（1）通过改变技术站内列车的解体编组顺序、加开10005次列车的方法，对原有的车流接续计划进行优化，使得货车在站总停留时间和平均停留时间相比原方案均降低了7.4%，并且在阶段结束后，调车场没有出现残存车，有效提高了货车周转效率。

（2）通过考虑列车加开的技术站车流接续计划优化模型，降低了技术站内的总体负荷情况，避免了技术站各子系统间拥堵情况的发生。

4 结 论

本文在考虑技术站列车加开的情况下，分析列车加开的基本条件，建立了技术站配流模型，通过算例分析验证，可以得到如下结论：

（1）面对技术站出现拥堵的情况时，考虑加开列车这一方案比单纯优化技术站配流方案具有更高的适用性，能有效避免技术站发生拥堵情况；

（2）采用考虑列车加开的技术站车流接续方案，虽然使原有列车运行图的稳定性有所下降，但货车在站滞留时间大幅缩短，有利于加快货车周转，提高技术站的车流组织效率。