赏析2022年高考数学全国I卷第21题

浙江工业大学附属德清高级中学 施利强 (邮编：313200)

1 试题呈现，解法探究

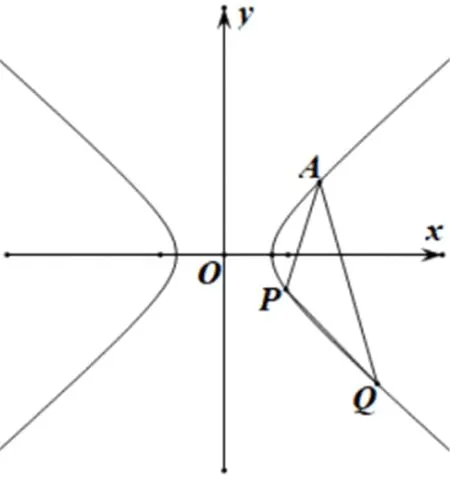
图1

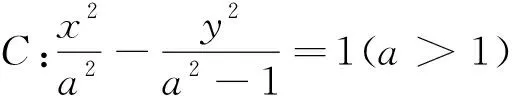
(1)求l的斜率；

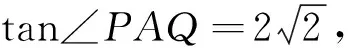
该试题让我们联想到2011年全国高中数学联赛第11题命题模型相关的经典试题，熟悉的模型下又有新意，以下笔者先呈现该试题的解法.

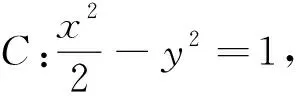
其中k>0，交点P(x1,y1)，Q(x2,y2).直线lPA与双曲线联立得(1-2k2)x2+(8k2-4k)x-8k2+8k-4=0，

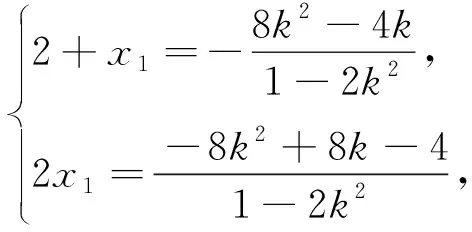
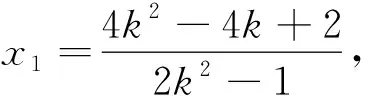
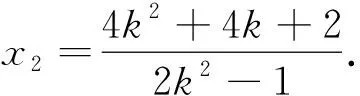
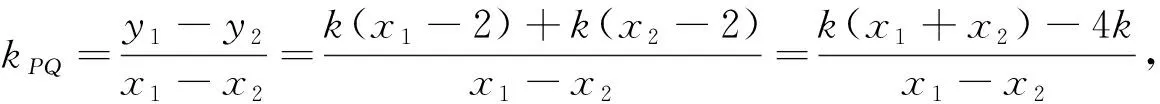
(2)设lAP,lAQ的倾斜角分别为α,β，则β=π-α，∠PAQ=π-2α，

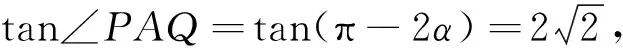
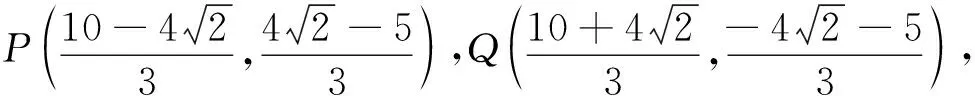
解析二设lPQ:y=tx+l，交点P(x1,y1)，Q(x2,y2)，与双曲线联立得

(1-2t2)x2-4tlx-2l2-2=0，

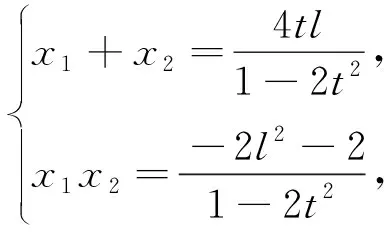
因为kAP+kAQ=0，

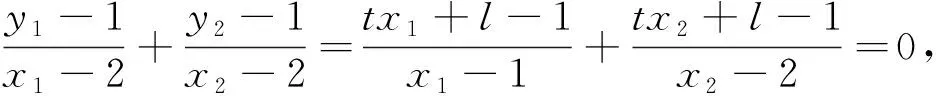
代入化简得(t+1)(l+2t-1)=0，当l+2t-1=0时，直线lPQ过(2,1)，不合，所以t=-1.

解析三设lPQ:m(x-2)+n(y-1)=1，直线lAP,lAQ的斜率为k1,k2，交点P(x1,y1)，Q(x1,y1).

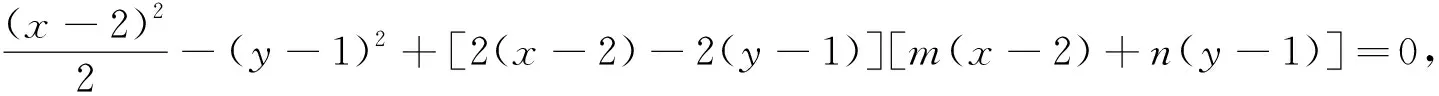
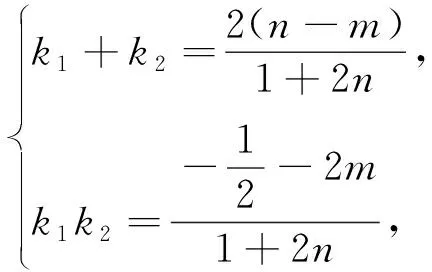
结合由解析一，可得

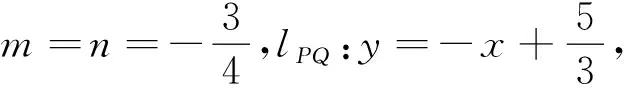
评注解析一与解析二解法较为自然，是该试题解决的常规方法.当试题的问题涉及斜率和时，解析三构造齐次方程也是常用方法，但是该解法技巧性较高，对学生的综合分析能力有较高的要求.

2 深度挖掘，命题探源

今年解析几何试题的命题背景是我们较为熟知的模型，在此之前，在该模型下也命制了较多高质量的高考试题，该题也可以看为2021年全国I卷21题解析几何试题命制模型下的特殊情形.

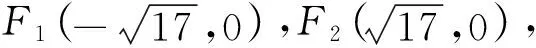
(1)求C的方程；

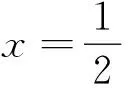
2021年解析几何试题的命制模型，即圆锥曲线中的割线定理，2022年解析几何试题可看成点T,A,P重合时的特殊情形，有较多文献对去年的试题进行了命题挖掘，也给出了较多的结论，一般都是利用直线的参数方程进行证明.在本文中，笔者另辟蹊径，引用了《圆锥曲线论》[2]第三卷中命题16和命题17，在两个命题的基础上对命题模型相关结论的几何意义进行了进一步的深度挖掘，文[1]中也将这两个命题作为文化背景给出，以下先给出这两个命题.

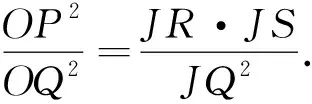
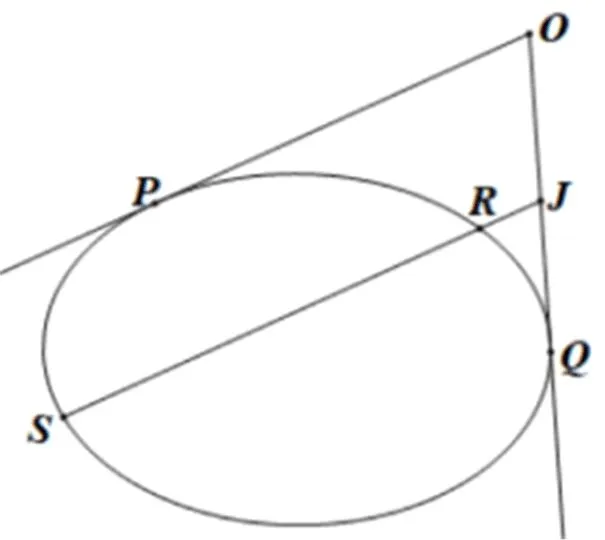
图2

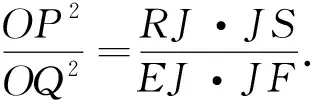
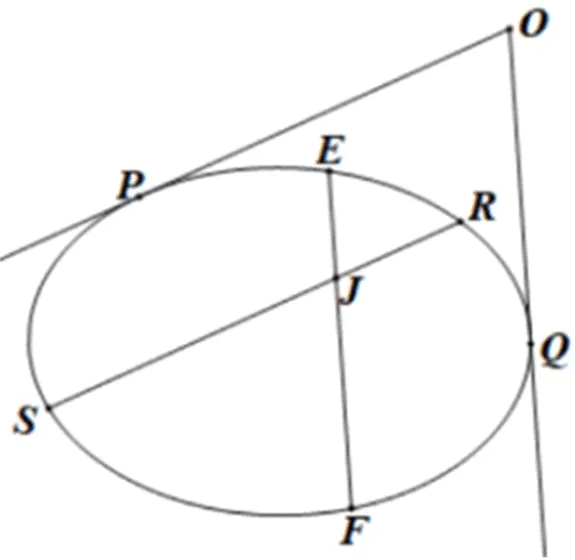
图3

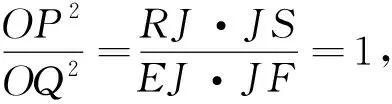
结论1过圆锥曲线内部或外部一点J作两条直线分别交圆锥曲线于E,F和R,S，

则R,S,E,F四点共圆的充要条件是直线RS与EF斜率互为相反数.

结论2过圆锥曲线内部或外部一点J作两直线分别交圆锥曲线于E,F和R,S，则直线RS与EF斜率互为相反数时，直线ER与直线SF，直线ES与直线RF倾斜角分别互补.

证明如图5，由结论1可知直线RS与EF斜率互为相反数时R,S,E,F四点共圆，点S,E和F,R可以看成过点T作两直线与圆锥曲线的交点，利用结论1可知直线ES与直线RF的倾斜角互补，同理直线ER与直线SF倾斜角互补.实际上，结论2也可以通过圆心角圆周角进行证明.

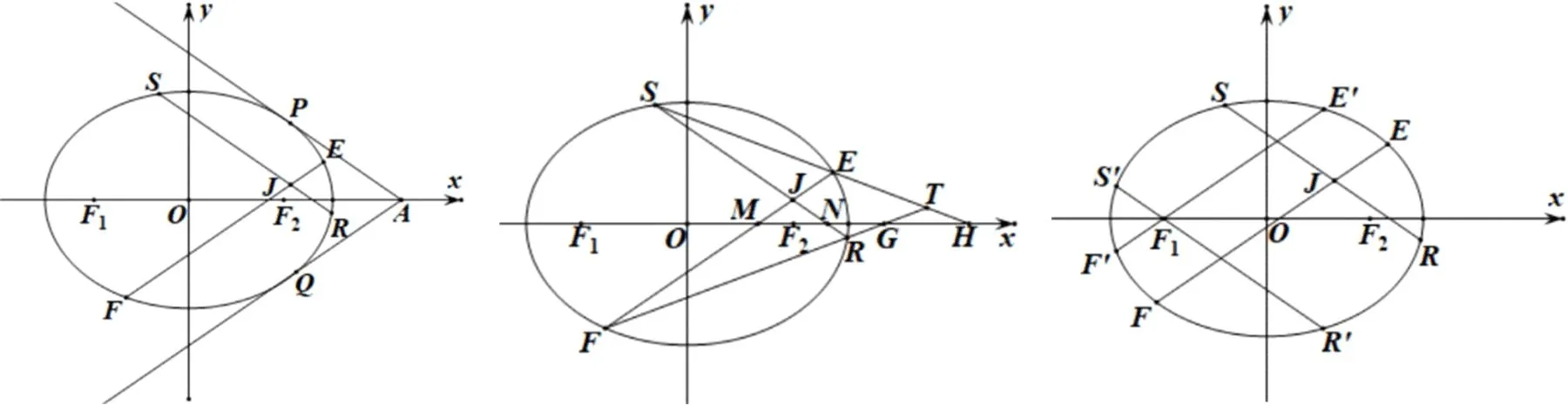
图4 图5 图6

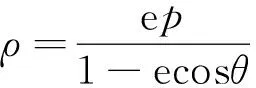
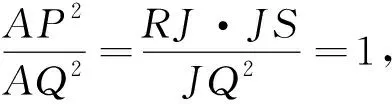
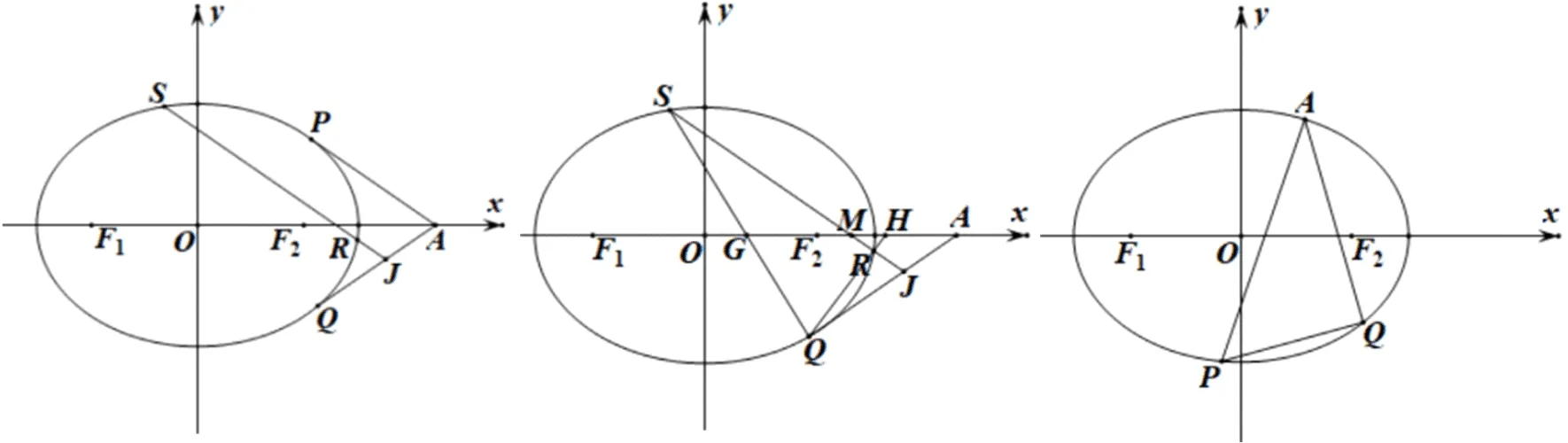
图7 图8 图9

结论3过圆锥曲线外一点J作圆锥曲线的切线和割线分别交于点Q和点S,R，则直线JQ与直线JS倾斜角互补的充要条件是直线QS与直线QR的倾斜角互补.

证明设直线QJ与直线SJ与x轴分别交于点A,M，直线QS与直线QR与x轴分别交于点G,H.由图8可得∠QGH=∠S+∠SMG，∠QHG=∠HQA+∠HAQ，因为∠S=∠HQA且∠SMG=∠HAQ，所以∠QGH=∠QHG，直线QS与直线QR的倾斜角互补.反之，当直线QS与直线QR的倾斜角互补时，可看成命题17的特殊情形，过点S,Q,R的外接圆与椭圆相切于点Q，直线QA为公切线，与以上证明类似可以说明直线JQ与直线JS倾斜角互补.

结论3也是今年高考试题的命制背景，运用该结论可得直线l的斜率为-1.最后利用直线的参数方程，对该试题模型下的三角形面积公式进行了推广.

结论4如图9，已知点A(x0,y0)是圆锥曲线上的一点，过点A分别作斜率为k,-k的两条直线交圆锥曲线于P,Q两点，则焦点在x轴上的椭圆或双曲线中

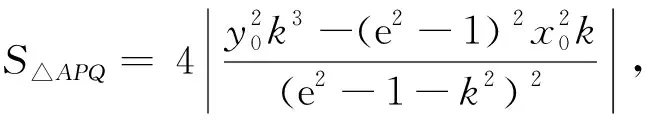
3 变式挖掘

至于此，笔者意犹未尽，一般在该模型下命制的相关试题都是给定定点，尝试以动点设置试题条件改编得到变式试题，以期对一线教师的教学带来思考与便利.

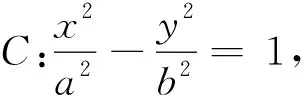
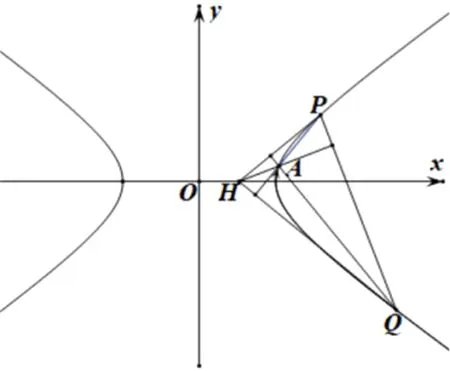
图14

(1)求双曲线方程；

(2)是否存在定值k，使得H点始终落在x轴上？若存在，且H点落在双曲线右顶点和右焦点之间时(包括右顶点和右焦点)，求△APQ面积的最大值，并求取最大值时A点的坐标.

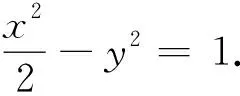
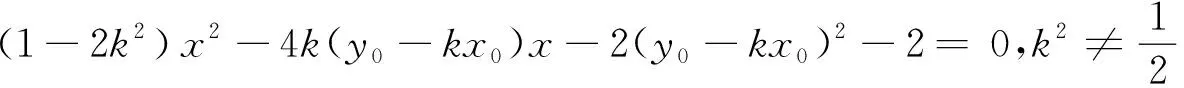
所以

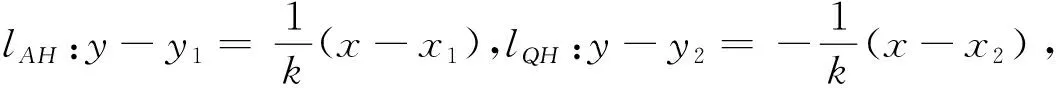
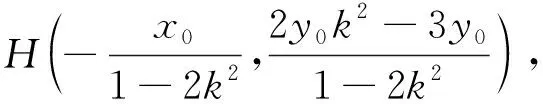
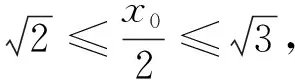
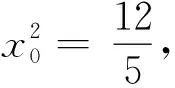
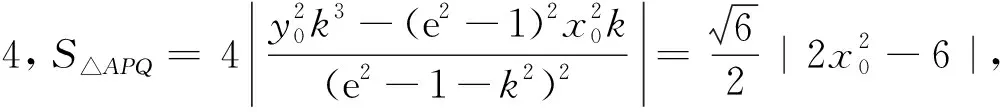
4 写在最后

2022年高考已落下帷幕，每年的高考都会给我们留下较多经典的试题.今年的全国I卷被誉为史上最难数学卷，以重思维少计算为命题原则，这也给我们一线教师提供了教学方向.在我们平时的教学过程中，应该多注重培养学生的思维能力和独立思考的能力，当学生具备严谨地分析能力和举一反三的能力时，才能以最高效的方式解答试题.