支持向量机辅助演化的算术优化算法及其应用
田 露,刘 升
上海工程技术大学 管理学院,上海 201620
近年来,启发式算法在工程优化问题中越来越受欢迎,由于它们具有易于实现、无需梯度信息、躲避局部最优等优势,可以很好地满足不同领域实际问题的需求[1]。目前启发式算法已被应用于参数优化、特征优化、集成约简、原型优化、加权投票集成以及核函数学习等机器学习领域[2-3]。
Abualigah等人于2021年受数学计算方法中算术运算符启发提出了算术优化算法(arithmetic optimization algorithm,AOA)[4]。该算法利用运算符的分布特性从候选解中寻找最优解,由于其具有较好的寻优性能,目前已被应用到一些问题中,如文献[5]使用差分进化算法增强AOA的局部开发能力,并应用于多阈值分割问题中;文献[6]使用高斯变异和正弦混沌策略改进AOA,以提升质子交换膜燃料电池模型识别的准确性;文献[7]使用拥挤距离机制和精英非优势排序策略改进AOA,并用于求解多目标优化问题;文献[8]将SMA和AOA结合并利用随机反向学习策略提高收敛速度,提出了随机反向学习策略的黏菌与算术混合优化算法;文献[9]将灰狼信息反馈机制与反向学习引入AOA,并对非线性收敛系数MOP建立修正模型,提出了具有激活机制的多头反向串联算术优化算法。
上述改进虽然提高了算法的寻优性能,但由于进化过程中种群规模始终不变,改进策略仅在有限的种群数量内增加了种群多样性。为了进一步提高算法性能,本文从增加演化过程中种群数量的角度对AOA进行改进。AOA算法的子代生成方式为仅向当前全局最优解靠近,该策略使种群中其他个体携带的信息没有得到充分利用,种群多样性也较差,算法极易陷入局部最优解。因此本文引入平衡优化器算法中的平衡池概念,充分利用种群中个体包含的信息,通过四种突变策略及其平均候选解,增加种群的多样性。但考虑到随着平衡池中个体数量的增加,个体评价次数也随之增加,同时平衡池中较差个体所携带的信息也会对算法演化产生不利影响。因此,本文使用支持向量机对平衡池中的个体进行分类,首先对适应度值和距离进行归一化处理,并将二者转化为个体留存率,用该指标将个体划分为优势个体和劣势个体;然后将其转化为训练集用以训练支持向量机模型;最后用训练好的模型从平衡池中选出优势个体,保留前N个个体用于构建下一代平衡池。通过将SVMAOA与其他算法在基准测试函数与特征选择问题上验证表明SVMAOA具有较优的性能。
1 算术优化算法
算术优化算法根据运算符不同的分布特性,在搜索空间内中寻找最优解。由于除法运算符(D)和乘法运算符(M)具有发散的性质,搜索过程中步长较长,可以保证在搜索前期对搜索区域充分探索,避免陷入局部最优解。而减法运算符(S)和加法运算符(A)具有收敛的性质,搜索过程中步长短,可以保证在搜索后期对在几个密集区域上对搜索区域进行深入探索搜索区域充分开发,增强局部寻优能力。
1.1 数学优化加速函数
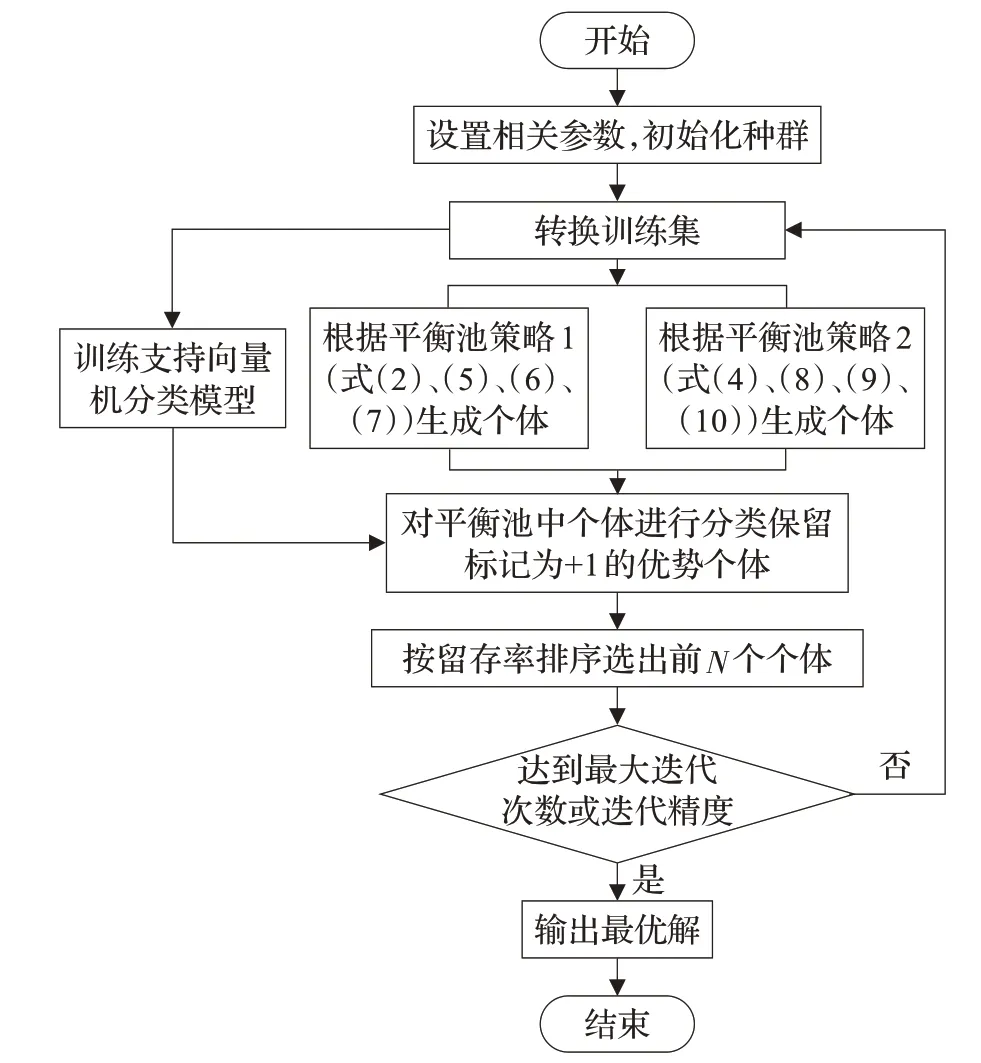
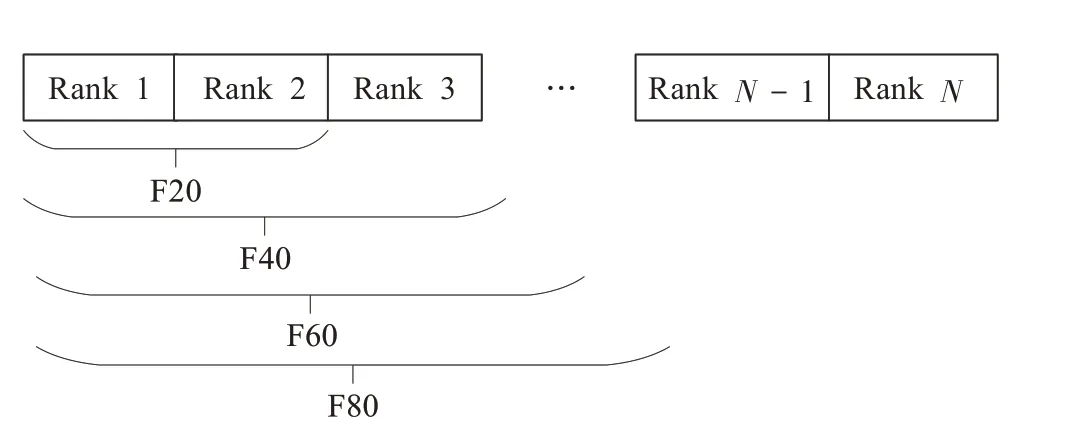
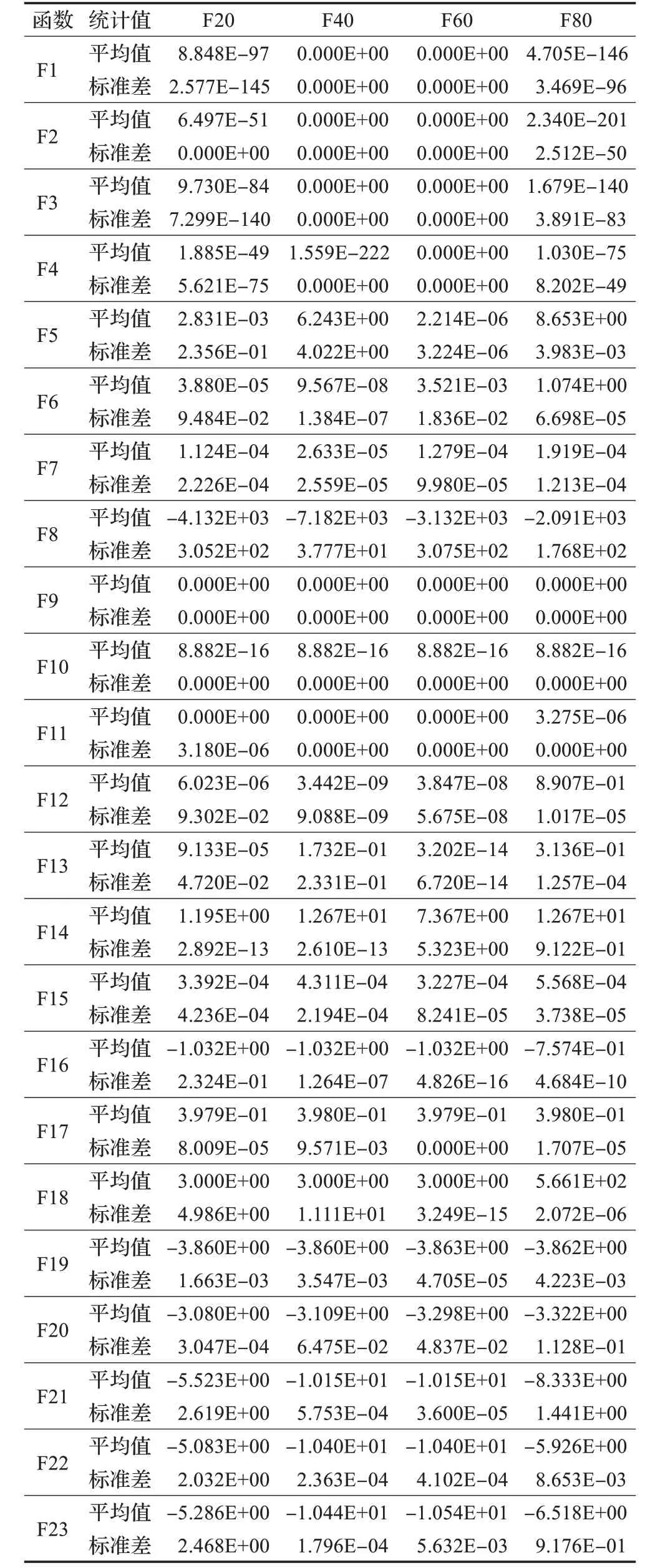
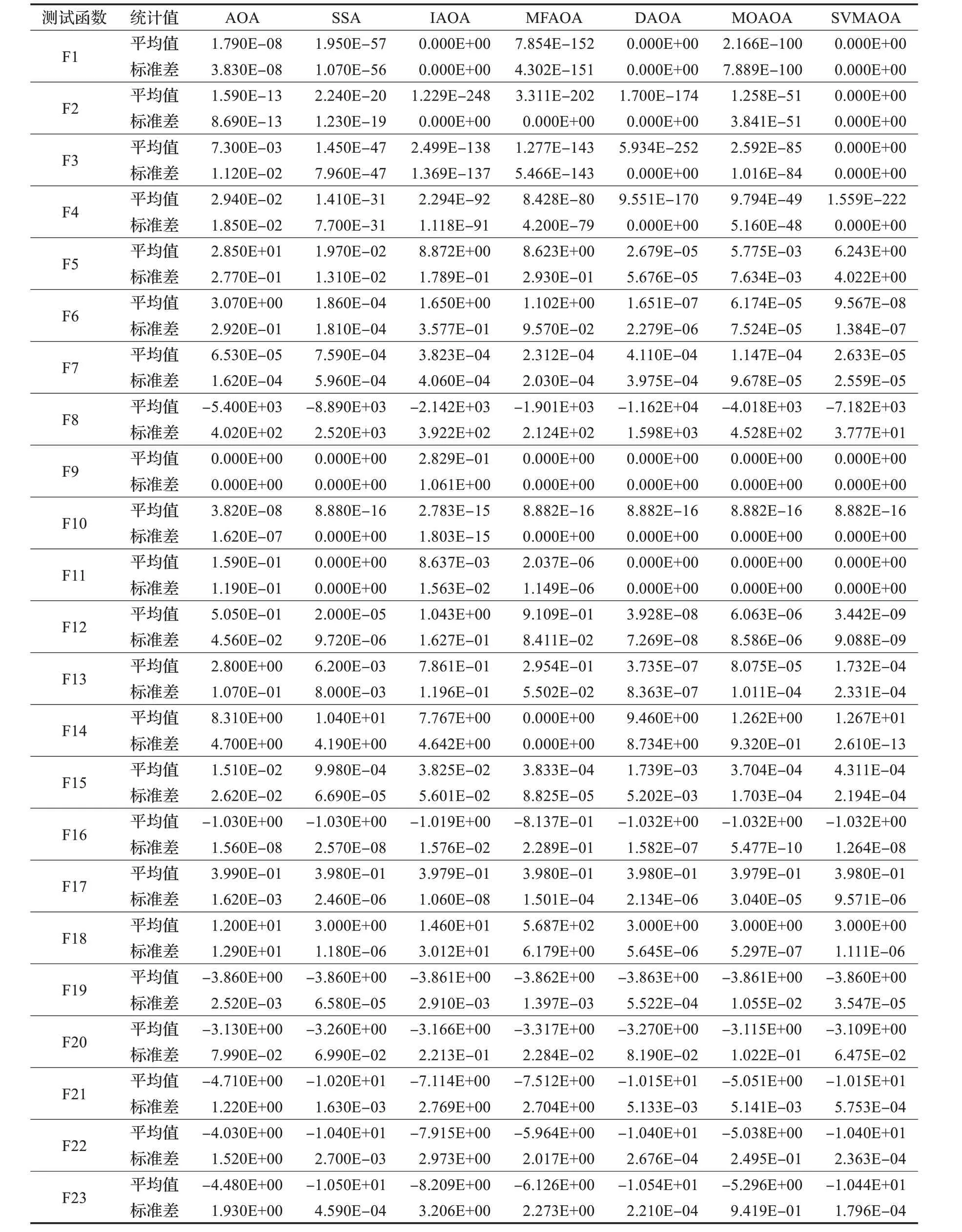
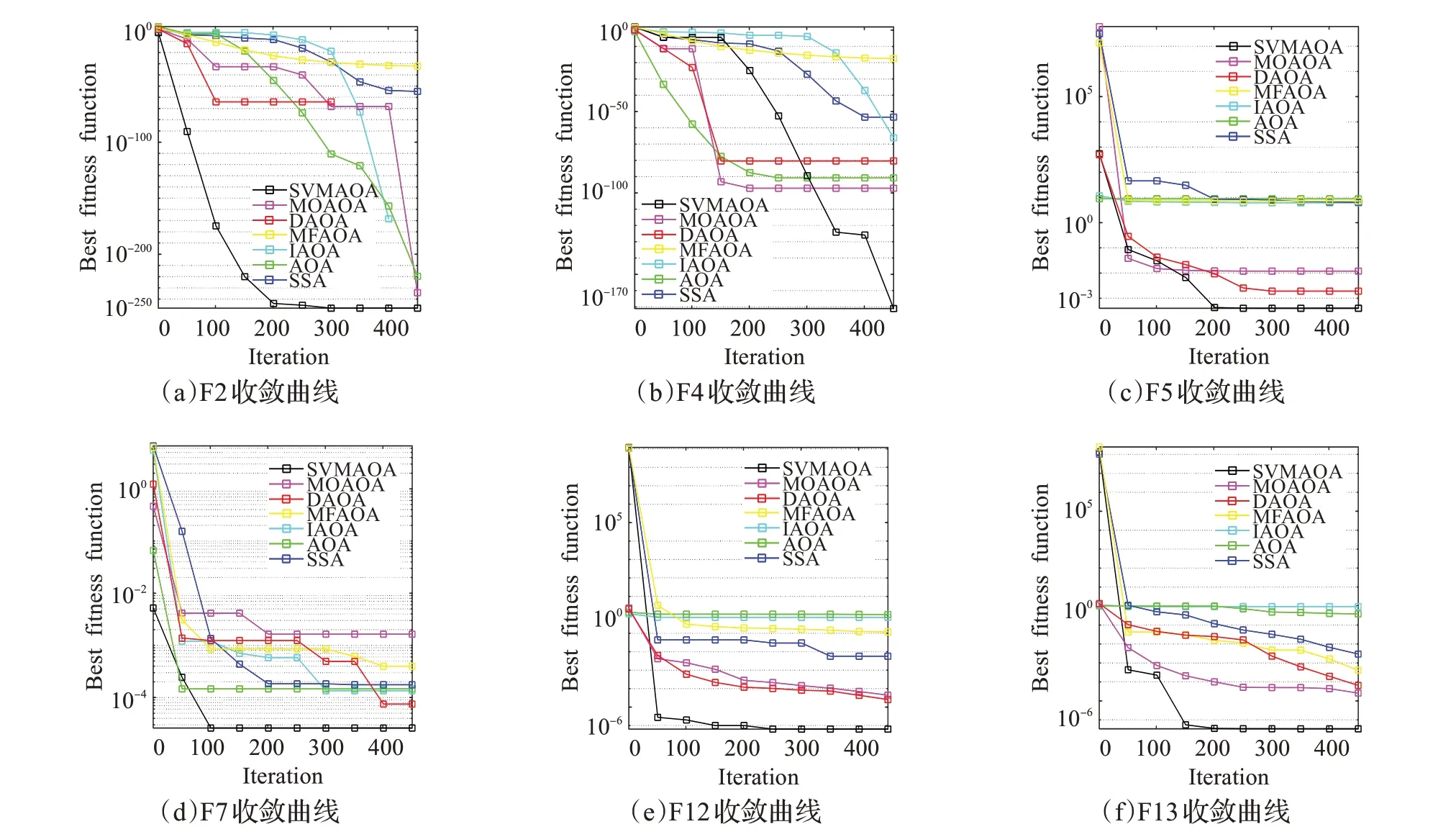
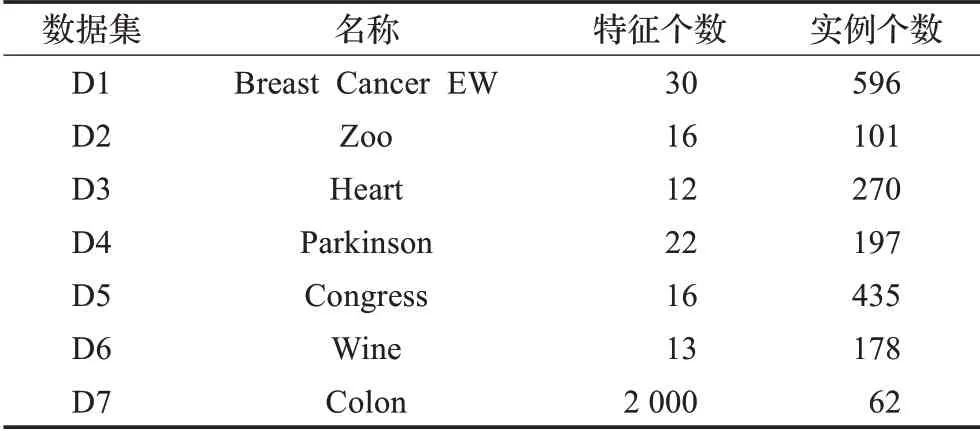
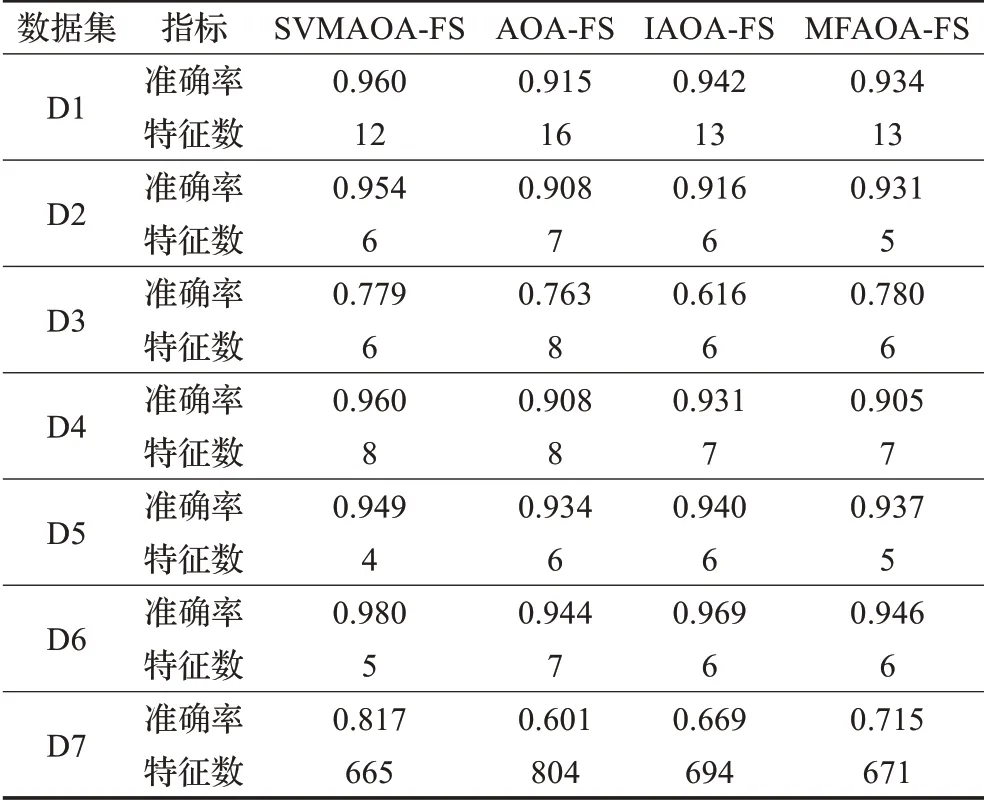
在算法开始寻优前,需要选择搜索阶段。设定随机参数r1∈[0,1]与数学优化加速函数(math optimizer accelerated,MOA)用于选择搜索阶段(即探索或开发)。当r1 其中,C_Iter为当前迭代次数,M_Iter为最大迭代次数。Min=0.2表示加速函数的最小值,Max=0.7表示加速函数的最大值。 AOA在全局探索阶段基于除法搜索策略和乘法搜索策略搜索,位置更新公式如下: 其中,r2∈[0,1],当r2<0.5时,采用除法策略,否则采用乘法策略。μ为搜索过程控制参数,用以调节搜索过程,值为0.499。 为探索解空间的不同区域,保证解的多样化,更新公式中考虑了一个随机参数,即数学优化概率(math optimizer probability,MOP),MOP计算公式如下: 其中,α为敏感参数,定义了迭代过程中的开发精度,值为5。 AOA在局部开发阶段基于加法搜索策略和减法搜索策略进行搜索。位置更新公式如下: 其中,r3∈[0,1],当r3<0.5时,采用减法策略,否则采用加法策略。 支持向量机(support vector machine,SVM)是机器学习领域中经典的分类算法之一,由Cortes等人于1995年提出[10]。SVM的核心思想是寻找一个保证分类精度的同时,使分类间隔最大化的最优分类超平面。算数优化算法在寻优过程中,用于将个体划分为优势个体和劣势个体,因此可以将其视作一个二分类问题。其中,种群中所有个体xi(i=1,2,…,N)为样本集,N为种群中个体数量,个体的优劣为yi={ } 1,-1。 AOA的个体更新方式为向当前全局最优个体收敛,这种更新策略虽然能够达到快速收敛的效果,但当前全局最优个体若为局部最优解而非真正的全局最优解时,该策略极易导致算法陷入局部最优。同时,AOA算法没有充分利用除当前全局最优个体以外的其他个体,忽略了种群其他个体所包含的信息,导致种群多样性和全局搜索能力较差。 因此,本文引入平衡优化器算法中平衡池的概念,池中除原始AOA算法子代生成方式外,还引入了基于成功历史的自适应差分算法(success-history based adaptive DE,SHADE)的四种突变策略(DE/rand/1、DE/best/1、DE/rand/2和DE/best/2)生成的个体,以及以上个体的平均候选解,并根据演化阶段自适应地选择策略。 在探索阶段,增加的两种子代位置生成公式和平均候选解公式如下: 在开发阶段,增加两种子代位置生成公式平均候选解公式如下: 其中,xri,t为第t代种群中除当前全局最优个体外随机选择的第i个个体,xpbest,t是从当前种群中随机选择适应度值排名在前100p%中的个体。 MOP为服从柯西分布的随机数,其中μMOP初始值为0.5,1/c∈[5,20]。 公式中的MOP参数随迭代次数的增加自适应地调整搜索步长。以上操作既保证了算法的收敛性,又避免仅向当前全局最优个体收敛,保持了种群多样性。本文使用测试函数对改进的SVMAOA算法与原始AOA算法的求解精度和收敛速度进行对比,以验证构建平衡池策略的有效性。 针对AOA算法种群多样性较差的特点,上文提出了构建平衡池策略以增加种群多样性。由于仅参考适应度值可能导致种群多样性的丧失,不能充分利用和探索未知的搜索空间,因此本文综合考虑适应度值和个体间距离,并将其转化为个体留存概率。同时当个体数量增加时,若对所有个体都进行适应度值评价,运行时间不可避免地会增加,因此本文使用支持向量机依据个体留存概率对平衡池中所有个体进行分类,在进化过程中保留优势个体,丢弃劣势个体。 分类问题中的数据集以(X,D)的形式存在,本文中子代个体为D为留存标志。将子代个体按留存率进行降序排列,并使用n%的比例对数据集进行划分,对前100p%的个体标记为1,代表保留,对剩余个体标记-1,代表丢弃。留存率由适应度值与个体间距离共同决定,为使适应度值与个体间距离处于同一数量级,对二者进行归一化处理,计算公式如下: 其中,ymax和ymin分别为最大和最小适应度函数值,Dmax和Dmin分别为Di的最大和最小值,ε为一个极小值以避免出现零除法。 使用支持向量机辅助进化策略步骤如下: 步骤1计算种群中每个个体的留存率; 步骤2根据留存率转换为训练数据集; 步骤3利用数据集训练分类器; 步骤4使用上一代保留的个体构建平衡池; 步骤5用分类器对个体分类,保留优势个体; 步骤6根据适应度值对优势个体排名,选择前N个个体作为下一代种群。 使用支持向量机辅助进化的算术优化算法(SVMAOA)伪代码如下: 开始 初始化主要参数设置初始化种群 计算种群中每个个体的留存率 根据留存率将其转换为训练数据集 利用数据集训练分类器 while t 根据式(1)更新MOA if r1 使用式(2)、(5)、(6)、(7)生成子代个体及其平均候选解放入平衡池 Else 使用式(4)、(8)、(9)、(10)生成子代个体及其平均候选解放入平衡池 end if 通过分类器对平衡池中个体进行分类,保留优势个体 对优势个体进行排序,保留前N个个体 t=t+1; end while 返回最佳位置 结束 SVMAOA具体实现流程如图1所示。 图1 SVMAOA算法流程图Fig.1 Flow chart of SVMAOA algorithm SVMAOA的计算复杂度分为以下几部分:初始化过程、训练分类器、构建平衡池解、对平衡池内所有个体进行分类以及排序。设算法的种群规模为N,问题维度为D,最大迭代次数为T,则算法的时间复杂度如下。 初始化阶段的复杂度为O(N×D),计算个体留存率为O(N);训练分类器的时间复杂度为O(N lg N);构建平衡池的时间复杂度为O(N×D×3);使用分类器对平衡池内所有个体进行分类的时间复杂度为O(N×D×3);设优势个体的比例为α,则计算优势个体留存率的时间复杂度为O(3×N×α),对优势个体排序的时间复杂度为O((N+3×α)lg(N+3×α))。 综上所述,SVMAOA的时间复杂度为O(T(3ND+(N+3Nα)lg(N+3Nα))。 定理1 SVMAOA在演化中全局最优适应度值是单调非增的,即f(Xg,t)≤f(Xg,1)。 证明 根据算法的选择策略,只有个体的适应度值小于全局最优值时,才对全局最优值进行更新,因此满足下式: 其中,Xg,t为第t代时全局最优个体的位置,因此全局最优解的适应度值单调不增,证明完毕。 定理2算法的状态空间内的随机过程是马尔科夫链。 证明 将状态空间从{X(t)}转移到{X (t+1)}的过程记为X(t+1)=T(X(t)),SVMAOA算法可以将此过程表示为: 其中,Ta代表初始化过程,Tb代表构建平衡池过程,Tc代表选择优势个体过程。可以看出,X(t+1)只与X(t)有关,且三个过程均依赖于X(t)而不是t,算法的状态空间内的随机过程是马尔科夫链,证明完毕。 定理3算法的状态空间{}X(t)收敛到全局最优子集M*的概率为1。 证明SVMAOA算法从{X(t)}转移到{X (t+1)}的状态转移概率为: 计算可得: 令 上式可表示为: 变换可得: 对两边求极限: 上述三个定理说明算法的状态空间是单调不增的马尔科夫链,且收敛于最优集的概率为1,由此可得算法具有全局收敛性。 本仿真测试环境为:仿真软件为MATLAB 2018b,操作系统Windows 10,内存为16.0 GB,CPU为AMD Ryzen 5 4600U,主频2.10 GHz。 为了选取合适的数据集划分比例以及验证SVMAOA的优化效果和稳定性优于其他算法,本文对多个不同特点的测试函数进行函数优化的对比测试,测试函数及其具体信息如表1所示。 表1 测试函数Table 1 Test function 由于数据集中优势个体与劣势个体比例的划分也对分类器的性能有显著影响,优秀样本过多会导致一些劣势个体无法区分,优秀样本太少会导致一些优势个体分类错误。本文分别对适应度值排名前20%、40%、60%和80%的优势个体打标签+1,对剩余劣势个体打标签-1,以用来确定对算法寻优性能最佳的数据集划分策略,上述划分策略分别用F20、F40、F60和F80表示,见图2。 图2 训练集转换策略示意图Fig.2 Schematic diagram of training set conversion strategy 通过基准测试函数对上述策略进行实验测试,种群规模设定为30,维数设定为30,最大迭代次数设定为500。 从表2可以看出,F40策略的SVMAOA可以使较多测试函数的寻优精度达到最优,同时具有一定稳定性,整体表现最好。在接下来的实验中,选择F40的训练集划分策略。 表2 四种策略实验结果Table 2 Experimental results of four strategies 本文将改进算法(SVMAOA)与原始算法(AOA)、其他学者改进的改进算法(DAOA、MOAOA、MFAOA[11]、IAOA[12])以及其他算法(SSA[13])进行比较。种群规模设定为30,维数设定为30,最大迭代次数设定为500,各算法的参数设置见表3。 表3 对比算法参数Table 3 Compare algorithm parameters 本文使用Booth函数对AOA与SVMAOA迭代典型时刻的种群分布图进行对比,以验证构建平衡池的策略可以有效提升种群。Booth函数基本信息如表1所示,两种算法在第5、50和100次迭代时刻的种群分布如图3所示。 图3中,迭代初期时AOA种群中有部分个体重叠,种群多样性较差,且种群分布范围较小;而SVMAOA中种群分布更均匀,搜索空间更大,种群多样性更佳。当迭代到50次时,AOA中子代的分布以最优解的横纵坐标为参考,呈现十字形,而SVMAOA在平衡池三种子代生成策略的作用下,使子代生成过程不再仅以最优解为参照,此使种群以环状的分布围绕在最优解附近,明显改善了AOA种群分布图中的十字分布。当迭代100次时,AOA个体在原始的子代生成策略作用下,仍保持十字分布的状态,有很大一部分个体没有搜寻到最优个体。而SVMAOA中的大部分个体已经搜寻到(1,3)点,这是由于支持向量机分类器辅助演化过程,减少了评价次数,加快了种群的收敛速度。 图3 种群多样性对比图Fig.3 Comparative map of population diversity 本文通过23个基准测试函数对算法性能进行对比实验,为了避免偶然性带来的结果偏差,算法在每个基准测试函数上运行30次并对其求均值和标准差,以对比算法的求解精度与稳定性,实验结果见表4。 表4 测试函数实验结果Table 4 Experimental results of test function F1~F7为单峰函数,一般用于检测算法的全局寻优性能。SVMAOA与原始AOA算法和SSA算法相比较,平均寻优精度和标准差均有很大的提升,SVMAOA具有最佳的寻优性能。与改进算法相比较,除在F5函数上SVMAOA的平均寻优精度和标准差略差于DAOA算法以外,在其他测试函数中平均寻优精度和标准差都表现最优,SVMAOA算法相比于其他基于AOA的改进算法寻优性能最佳。总体看来,SVMAOA在单峰测试函数中表现出较优的寻优性能。 F8~F23为多峰函数,一般用来评价算法的局部寻优性能。SVMAOA与原始AOA算法相比较时,在F18函数上,两种算法寻优精度一样,但是SVMAOA算法的标准差较小,稳定性较高,在其他多峰测试函数中SVMAOA的最优解平均寻优精度和标准差均有很大的提升。与SSA相比较时,在F8函数上,SVMAOA算法平均寻优精度虽略差于SSA算法,但标准差却较小,算法在该函数上表现较稳定。在F13函数上,SVMAOA的平均寻优精度和标准差略差于SSA算法。在F14函数上,虽然SVMAOA相较于SSA平均寻优精度虽略低,但标准差却远小,改进算法的鲁棒性与其相比具有优势。在F14、F15函数上,SVMAOA的平均寻优精度优于SSA,但标准差却略高。在其他多峰测试函数上,SVMAOA的平均寻优精度和标准差都表现最佳。与其他改进算法相比较时,在F8函数上,DAOA的平均寻优精度略优于SVMAOA。在F13、F20函数上,DAOA的平均寻优精度略和标准差均优于SVMAOA。在F14函数上,MOAOA的平均寻优精度略优于SVMAOA。在F16、F17、F18函数上,SVMAOA相较于IAOA的平均寻优精度较高,但标准差却略差。在其他多峰测试函数中,SVMAOA相较于其他基于AOA改进的算法均表现出最佳的寻优精度和稳定性。总体看来,在多峰测试函数中,SVMAOA具有一定的竞争力。 以上实验结果说明平衡池策略有效地增加了提升了算法的全局寻优性能和局部寻优性能,为了进一步说明使用支持向量机分类策略可以有效地筛选优势个体,避免劣势个体对演化过程产生干扰,提升收敛速度,本文通过测试函数的迭代收敛曲线图验证SVMAOA算法的收敛速度。从图4可以看出,SVMAOA在收敛速度上也优于其他算法。 图4 收敛曲线图Fig.4 Convergence curve 为检验SVMAOA算法与其他算法的显著性差异,本文使用Wilcoxon秩和检验进行验证。在α=5%显著性水平下,若p<0.05则说明算法具有显著差异,反之则说明算法差异不显著。本文将SVMAOA与AOA、SSA、IAOA、MFAOA、DAOA、MOAOA在23个基准测试函数上进行30次运算,结果见表5。其中,N/A表示算法结果接近,无法进行显著性判断。在23个基准测试函数中,多数实验结果均小于0.05,说明SVMAOA的优越性在统计上是显著的。对于函数F9、F10和F11,SVMAOA与其他算法间的差异不明显,说明算法性能相当。 表5 Wilcoxon秩和检验结果Table 5 Wilcoxon rank sum test results 特征选择作为特征工程的关键环节,不仅可以剔除无关特征、提高算法的学习效率[14],还能从数据集中寻找最优特征子集[15],提高模型精确度。本文将选取尽可能少的特征得到较高的分类准确率作为目标,利用SVMAOA算法解决特征选择问题。 SVMAOA用于求解特征选择问题时,个体代表一组特征子集,种群维度为数据集中特征数。由于特征选择可以视作离散空间中的优化问题,故本文基于二进制编码方法,使用Sigmoid函数将个体向量转化至0到1的区间内,见式(24)。当值大于0.5时,将其置为1,反之置为0,0和1分别表示对应维度的特征没有被选择和被选择。 v为了通过尽可能少的特征得到较高的分类准确率,本文将以式(25)作为适应度函数[17]: 其中,α和β为分类准确率和特征子集长度的控制权重,α∈[0,1],β=1-β,本文α取0.85。γDR(D)为KNN(KNearest Neighbors)分类器错误率,k=5。||R为个体中被选择的特征数,||N为数据集中特征数。 为评价SVMAOA用于求解特征选择问题的优劣,本文选取分类准确率与特征选择个数作为衡量指标,分 类准确率定义见式(26): 其中,TP为真正例样本数,TN为真负例样本数,P为正例样本数,N为 为验证算法在特征选择问题中的性能,本文选用UCI中的7个数据集上进行测试,数据集信息见表6。 表6 实验数据集Table 6 Experimental datasets 本文将SVMAOA并与原始AOA算法、其他学者改进算法以及其他群智能优化算法进行对比,所有算法独立运行10次,种群规模为30,最大迭代次数为100次,各算法参数设置见表3,实验结果见表7。 表7 特征选择实验结果Table 7 Experimental results of feature selection 根据实验结果可以看出,本文改进的SVMAOA算法用于求解特征选择问题时,在所有数据集上的分类准确率均高于原始AOA算法和其他学者改进的算法。在D1、D3、D5、D6和D7数据集上数据集特征子集个数少于其他算法,在D2和D4数据集上略多于MFAOA算法。总体看来,在特征选择问题中,本文提出的SVMAOA算法与其他算法相比表现出色,能够有效地剔除无关特征,寻找到最优特征子集,提高模型精确度。 为了克服AOA无法充分利用个体信息、种群多样性较少等问题,构建了包含四种突变策略及其平均候选解的平衡池,充分利用种群个体所携带的信息,增加种群多样性;并且通过支持向量机分类模型对平衡池中个体进行分类,以减少由于个体数量增多导致的评价次数增加,同时避免劣势个体在演化过程中对算法造成的不良影响,逃离局部最优解,使得算法获得更好的收敛精度;最后根据留存率筛选个体,并用于下一代平衡池的构建。本文通过基准测试函数、统计检验Wilcoxon秩和检验和多样性分析验证算法性能,将SVMAOA与其他改进优化算法、原始优化算法进行对比,并在7个UCI标准数据集中进行特征选择实验,结果表明SVMAOA算法具有更优的性能。 在未来的工作中,可以尝试不同的平衡池更新策略。此外,还可以尝试使用不同的分类器,以及不同的数据集划分方式以增强算法性能。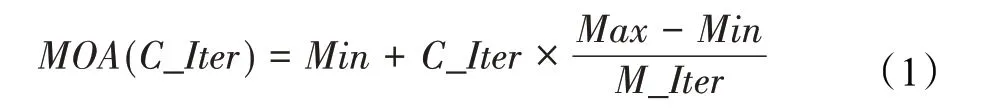
1.2 探索阶段
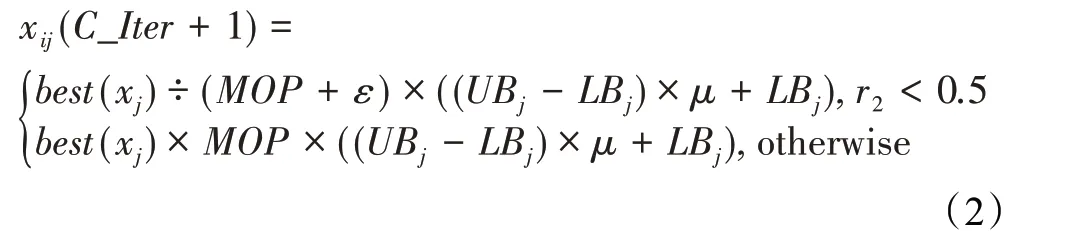
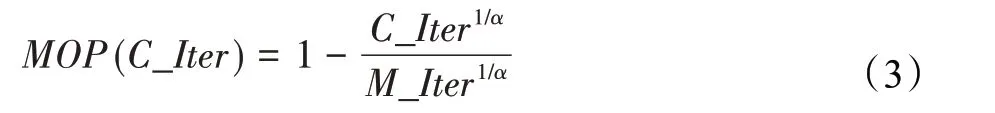
1.3 开发阶段
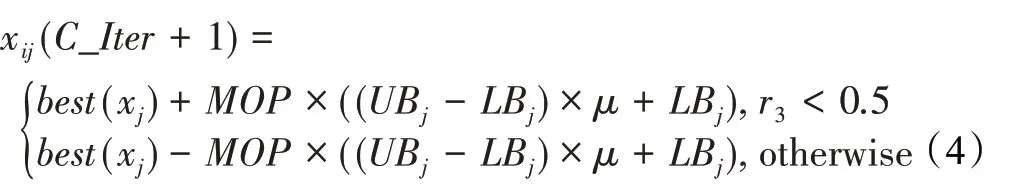
2 支持向量机
3 支持向量机改进的算术优化算法
3.1 构建平衡池



3.2 支持向量机分类策略
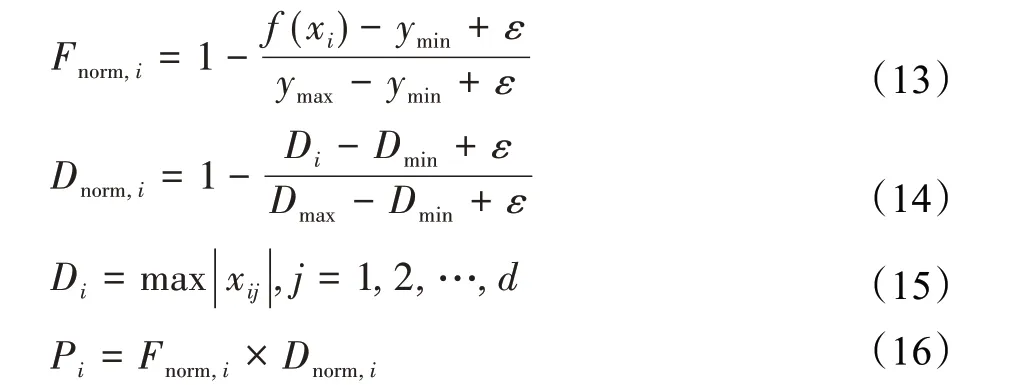
3.3 时间复杂度
3.4 收敛性分析
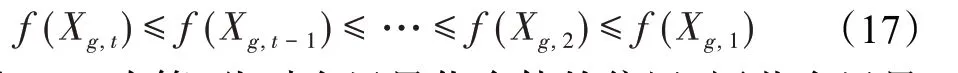
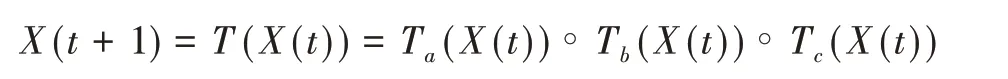
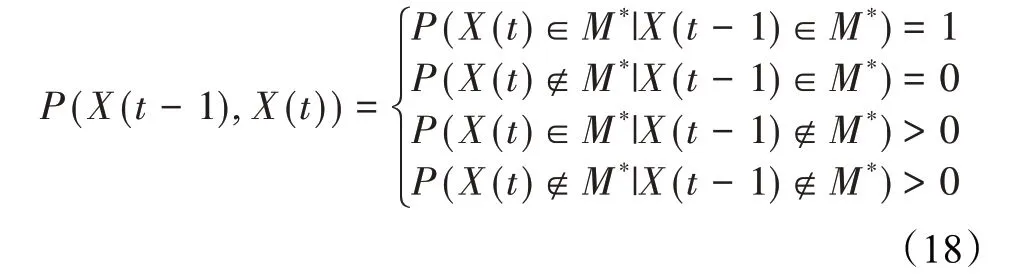
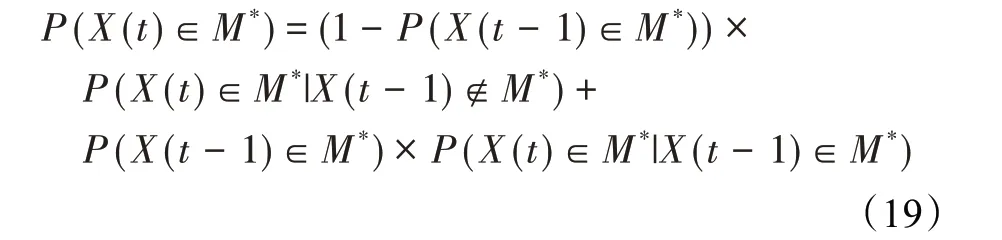
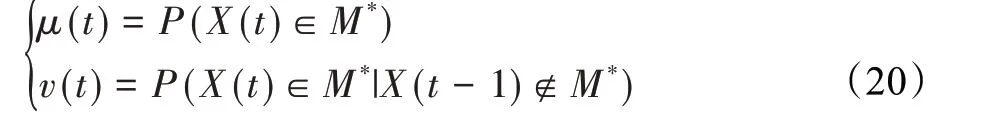
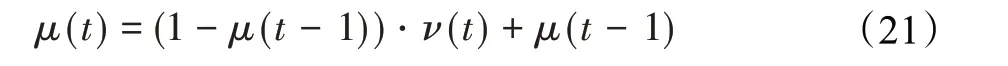
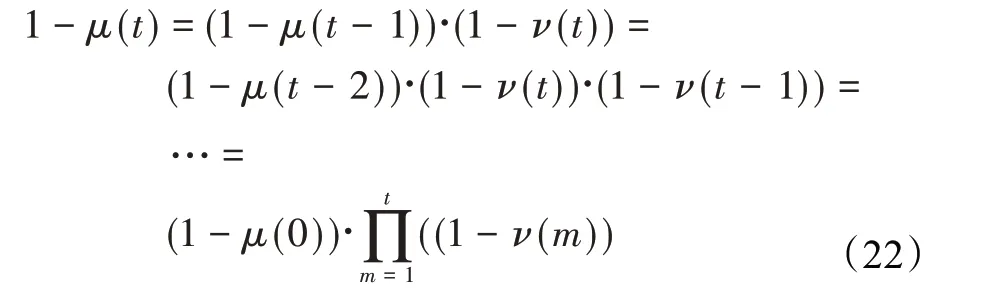
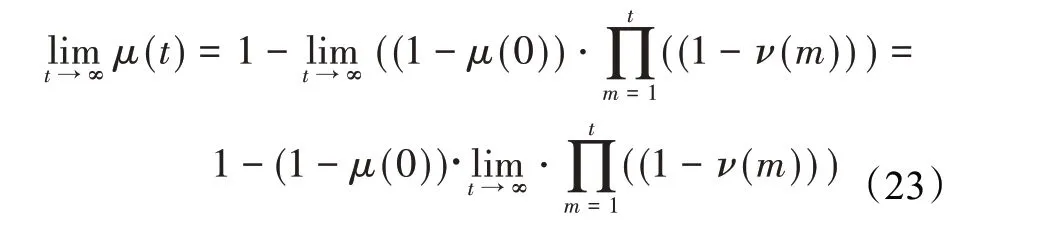
4 实验仿真与结果分析
4.1 仿真实验环境
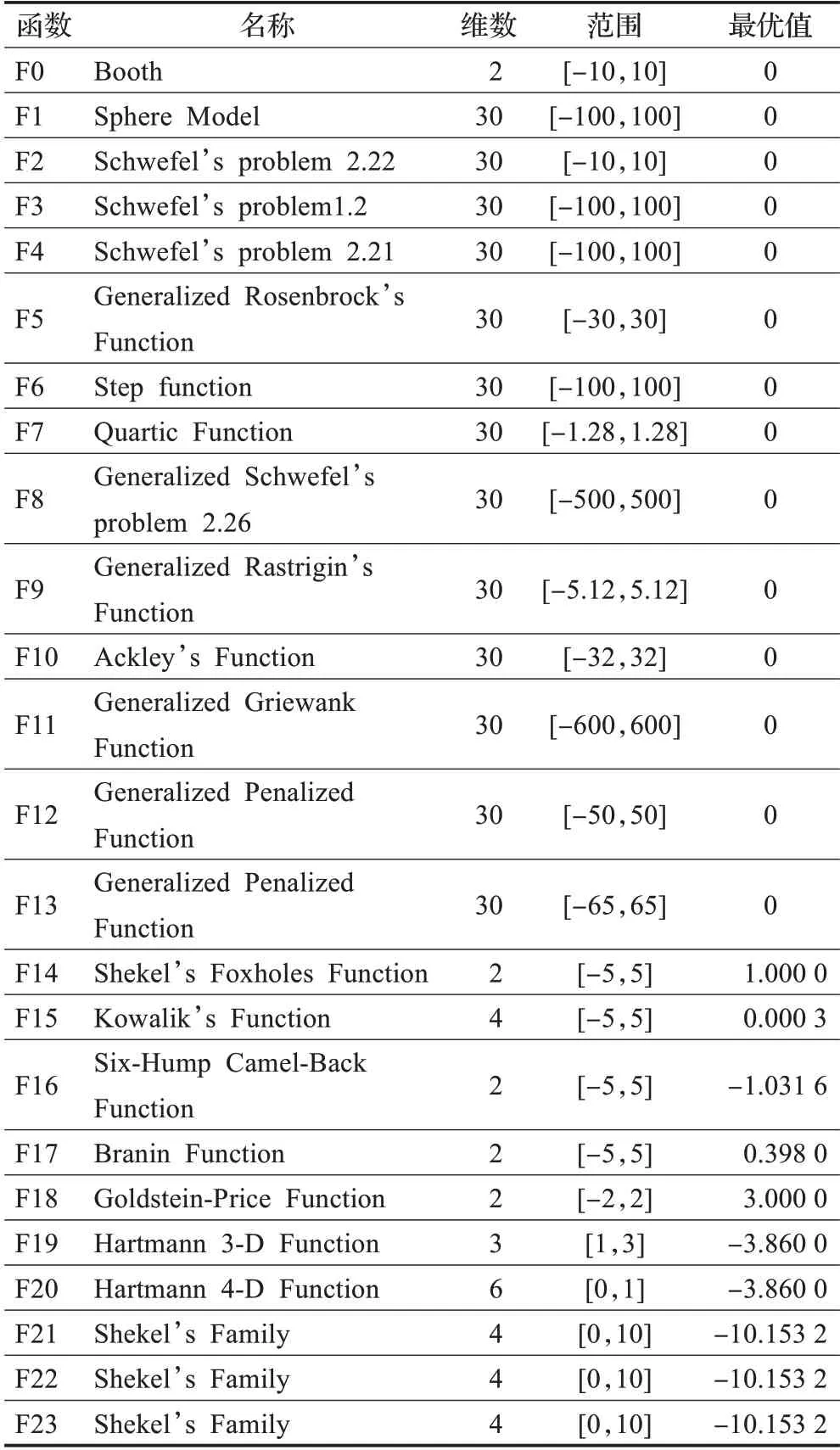
4.2 测试函数
4.3 参数选择
4.4 对比算法与参数设置

4.5 种群多样性分析

4.6 求解精度与收敛性分析
4.7 Wilcoxon秩和检验

5 SVMAOA用于特征选择问题
5.1 建立模型

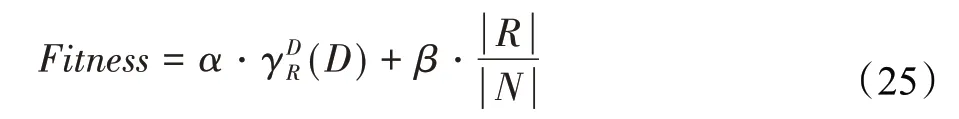

5.2 实验结果
6 结束语

